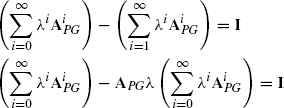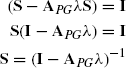11.7 Graph Kernel

A graph kernel is a kernel function that compares different graphs. We use such a graph kernel to compare two hyponymy hypotheses with each other. In particular, we compare by means of a graph kernel the SNs with each other from which the hypotheses were extracted from. There exist a lot of different types of graph kernels. The graph kernel of Borgwardt and Kriegel [27] compares the shortest paths in both graphs. These paths are determined for each graph separately. Two comparison functions were tested to compare the graph lengths: the product of the lengths and the function that takes the value of one if both lengths are identical and zero otherwise. The graph kernel value is then given by the sum of all such comparison function values iterating over all possible pairs of nodes in the two graphs. Kashima et al. [28] generate randomly common walks on the two graphs and count the number of walks that both graphs have in common. Another approach of Kashima, which he devised together with Hido, is to compare special kind of hash values computed for each graph [29].

Our work is based on the graph kernel as proposed by Gärtner et al. Like the approach of Kashima et al., the idea of this graph kernel is that graphs are similar if they share a lot of walks. Let us review some graph definitions before further explanations. A directed nonuniquely labeled graph is given by a set of nodes and arcs: G = (V, E). Each node and arc is assigned a label: label: G ∪ E → A^* where A is a given alphabet. This function is not injective, which means that different nodes or arcs can be mapped to the same label. A path in this graph is defined as a subgraph with a set of nodes and arcs E = {e₀, . . ., e_k} with and where all s must be distinct [30]. In contrast to a path, the same arc can be visited twice in a walk, which means that E is no longer a set but a sequence. Gärtner et al. use common walks instead of common paths because his proposed common walk kernel can easily be computed by matrix multiplications. For our hyponymy extraction scenario, we allow to follow an arc against the direction of the arc too if the associated arc in the other graph is also followed against its direction.

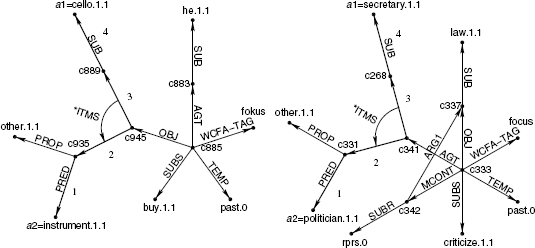
An example of a common walk in two SNs is given in Figure 11.3. Before calculating the common walks, the hyponym and hypernym candidates are replaced by fixed variables (here a1 and a2), which allows it to identify common walks involving hypernym and hyponym candidate nodes between SNs for sentences even if the hypernyms and hyponym candidates of the two sentences are different. In this way, the generality is increased.

Figure 11.3 A common walk/path of length 4 in the disordered graphs.

The calculation of the kernel value is based on the product graph (PG) representation of the two graphs G₁ and G₂. These graphs are also called factor graphs of the product graph. The node set PV of the product graph consists of pairs of nodes of the two factor graphs. The first component of such a pair is a node of the first factor graph, the second component a node of the second graph, and both nodes must be assigned the same label. For our semantic network scenario, the label of a node is assigned the concept name if the concept is lexicalized (e.g., school.1.1) or anon (e.g., if the concept is named c935) otherwise. Therefore, two nonlexicalized nodes always show up together as a node pair in the product graph.

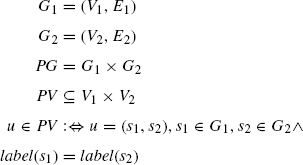
In contrast to Gärtner et al., we also identify nodes with each other if the labels are not identical, but the associated concepts are synonymous.

An arc e = (u₁, u₂) belongs to the product graph, if there exist an arc between the first node components of u₁ and u₂ in the first factor graph and an arc between the second node components in the second factor graph.

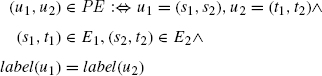
The adjacency matrix A of the product graph is given by

where n is the number of nodes in the product graph. An entry (x, y) in the adjacency matrix of the product graph is one iff there exists one common walk from node u_x to u_y or from node u_y to u_x of length one. Thus, basically an undirected graph model is used in the product graph with the exception that the orientations of the two identified arcs in the two compared graphs have to be identical. More generally, there are k common walks of length i from node x to node y iff where is the adjacency matrix taken to the ith power.

The total graph kernel value is then given by⁴

where and λ < 1. λ is a discounting factor and causes long common walks to be weighted less than short ones. This sounds quite irritating at first since a long common walk is a stronger indication of similarity than a short one. But a long common walk always implies a lot of shorter common walks. In this way, a long common is overall weighted more than a short one. ι is a vector consisting of only ones. ι^TMι (ι^T denotes the transposed vector) causes the entries of the surrounded matrix to be summated. is defined to be the identity matrix I. There is an analytical solution of this infinite sum if this sum converges. This becomes obvious after several transformations

(11.5)

Let S be . Then Equation (11.5) can be rewritten as

(11.6)

Since matrix inversion is cubic in runtime, the kernel can be computed in , where n is the number of nodes in the product graph.