1.4 Reconstruction of Biological Networks

In this section, we describe some existing approaches to reconstruct directed and undirected biological networks from gene expression data and gene sets. To reconstruct directed networks from gene expression data, we present Boolean network, probabilistic Boolean network, and Bayesian network models. We discuss cGraph, frequency method and NICO approaches for network reconstruction using gene sets (Fig 1.4). Next, we present relevance networks and graphical Gaussian models for the reconstruction of undirected biological networks from gene expression data (Fig 1.5). The review of models in case of directed and undirected networks is largely based on Refs. [6–8,17–20] and [2,3,13,32], respectively.

Figure 1.4 (a) Representation of inputs and Boolean data in the frequency method from Ref. [18]. (b) Network inference from PAK pathway [67] using NICO, in the presence of a prior known end points in each path [68]. (c) The building block of cGraph from Ref. [17].

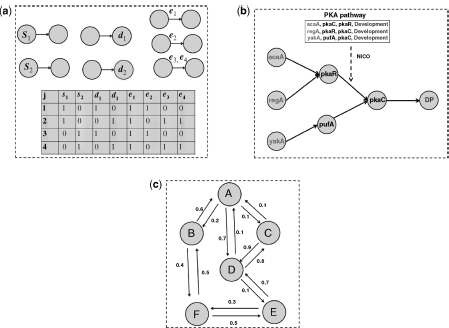
Figure 1.5 Comparison of correlation-based relevance networks (a) and partial correlation based graphical Gaussian modeling (b) performed on a synthetic data set generated from multivariate normal distribution. The figures represent estimated correlations and partial correlations between every pair of genes. Light to dark colors correspond to high to low correlations and partial correlations.

Although the aforementioned approaches for the reconstruction of directed networks have been developed for specific type of genome-wide measurements, they can be unified in case of binary discrete data. For instance, prior to infer a Boolean network, gene expression data is first discretized, for example, by assuming binary labels for each gene. Many Bayesian network approaches also assume the availability of gene expression data in a discretized form. On the other hand, a gene set compendium naturally corresponds to a binary discrete data set and is obtained by considering the presence or absence of genes in a gene set.

1.4.1 Reconstruction of Directed Networks

1.4.1.1 Boolean Networks

Boolean networks [4–6], present a simple model to reconstruct biological networks from gene expression data. In the model, a Boolean variable is associated with the state of a gene (ON or OFF). As a result, gene expression data is first discretized using binary labels. Boolean networks represent directed graphs, where gene regulatory relationships are inferred using boolean functions (AND, OR, NOT, NOR, NAND).

Mathematically, a Boolean network G(V, F) is defined by a set of nodes V = {x₁, . . ., x_n} with each node representing a gene, and a set of logical Boolean functions F = {f₁, . . ., f_n} defining transition rules. We write x_i = 1 to denote that the ith gene is ON or expressed, whereas x_i = 0 means that it is OFF or not expressed. Boolean function f_i updates the state of x_i at time t + 1 using the binary states of other nodes at time t. States of all the genes are updated in a synchronous manner based on the transition rules associated with them, and this process is repeated.

Considering the complicated dynamics of biological networks, Boolean networks are inherently simple models which have been developed to study these dynamics. This is achieved by assigning Boolean states to each gene and employing Boolean functions to model rule-based dependencies between genes. By assuming only Boolean states for a gene, emphasis is given to the qualitative behavior of the network rather than quantitative information. The use of Boolean functions in modeling gene regulatory mechanisms leads to computational tractability even for a large network, which is often an issue associated with network reconstruction algorithms. Many biological phenomena, for example, cellular state dynamics, stability, and hysteresis, naturally fit into the framework of Boolean network models [59]. However, a major disadvantage of Boolean networks is their deterministic nature, resulting from a single Boolean function associated with a node. Moreover, the assumption of binary states for each gene may correspond to an oversimplification of gene regulatory mechanisms. Thus, Boolean networks are not a choice when the gene expression levels vary in a smooth continuous manner rather than two extreme levels, that is, “very high expression” and “very low expression.” The transition rules in Boolean network models are derived from gene expression data. As gene expression data are noisy and often contain a larger number of genes than the number of samples, the inferred rules may not be reliable. This further contributes to an inaccurate inference of gene regulatory relationships.

1.4.1.2 Probabilistic Boolean Networks

To overcome the pitfalls associated with Boolean networks, probabilistic Boolean networks (PBNs) were introduced in Ref. [7] as their probabilistic generalization. PBNs extend Boolean networks by allowing for more than one possible Boolean function corresponding to each node, and offer a more flexible and enhanced network modeling framework.

In the underlying model presented in Ref. [7], every gene x_i is associated with a set of l(i) functions

(1.1)

where each corresponds to a possible Boolean function determining the value of x_i, i = 1, . . ., n. Clearly, Boolean networks follow as a particular case when l(i) = 1, for each i = 1, . . ., n. The kth realization of PBN at a given time is defined in terms of vector functions belonging to F₁ × . . . × F_n as

(1.2)

where 1 ≤ k_i ≤ l(i), and i = 1, . . ., n. For a given f = (f⁽¹⁾, . . ., f⁽ⁿ⁾) F₁ × . . . × F_n, the probability that jth function from F_i is employed in predicting the value of x_i, is given by

(1.3)

where j = 1, . . ., l(i) and The basic building block of a PBN is presented in Figure 1.6. We refer to Ref. [7] for an extended study on PBNs.

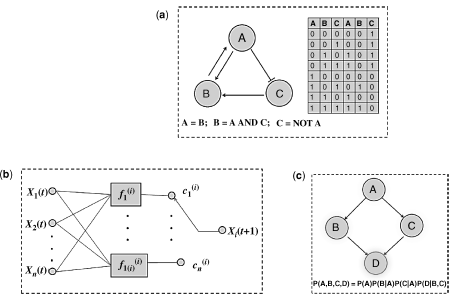
Figure 1.6 Network reconstruction from gene expression data. (a) Example of a Boolean network with three genes from Ref. [60]. The figure displays the network as a graph, Boolean rules for state transitions and a table with all input and output states. (b) The basic building block of a probabilistic Boolean network from Ref. [7]. (c) A Bayesian network consisting of four nodes.

It is clear that PBNs offer a more flexible setting to describe the transition rules in comparison to Boolean networks. This flexibility is achieved by associating a set of Boolean functions with each node, as opposed to a single Boolean function. In addition to inferring the rule-based dependencies as in the case of Boolean networks, PBNs also model for uncertainties by utilizing the probabilistic setting of Markov chains. By assigning multiple Boolean functions to a node, the risk associated with an inaccurate inference of a single Boolean function from gene expression data is greatly reduced. The design of PBNs facilitates the incorporation of prior knowledge. Although the complexity in case of PBNs increases from Boolean networks, PBNs are often associated with a manageable computational load. However, this is achieved at the cost of oversimplifying gene regulation mechanisms. As in the case of Boolean networks, PBNs may not be suitable to model gene regulations from smooth and continuous gene expression data. Discretization of such data sets may result in a significant amount of information loss.

1.4.1.3 Bayesian Networks

Bayesian networks [8, 9] are graphical models which represent probabilistic relationships between nodes. The structure of BNs embeds conditional dependencies and independencies, and efficiently encodes the joint probability distribution of all the nodes in the network. The relationships between nodes are modeled by a directed acyclic graph (DAG) in which vertices correspond to variables and directed edges between vertices represent their dependencies.

A BN is defined as a pair (G, Θ), where G represents a DAG whose nodes X₁, X₂, . . ., X_n are random variables, and Θ denotes the set of parameters that encode for each node in the network its conditional probability distribution (CPD), given that its parents are in the DAG. Thus, Θ comprises of the parameters

(1.4)

for each realization x_i of X_i conditioned on the set of parents Pa(x_i) of x_i in G. The joint probability of all the variables is expressed as a product of conditional probabilities

(1.5)

The problem of learning a BN is to determine the BN structure B that best fits a given data set D. The fitting of a BN structure is measured by employing a scoring function. For instance, Bayesian scoring is used to find the optimal BN structure which maximizes the posterior probability distribution

(1.6)

Here, we define two Bayesian score functions Bayesian Dirichlet (BD) score from Ref. [61] and K2 score presented in Ref. [62].

BD score is defined as [61]

(1.7)

where r_i represents the number of states of x_i, , N_ijk is the number of times x_i is in kth state and members in Pa(x_i) are in jth state, , , N_ijk ' are the parameters of Dirichlet prior distribution, P(B) stands for the prior probability of the structure B and Γ() represents the Gamma function.

The K2 score is given by [62]

(1.8)

We refer to Ref. [62, 61] for further readings on Bayesian score functions.

BNs present an appealing probabilistic modeling approach to learn causal relationships and have been found to be useful for a significant number of applications. They can be considered as the best approach available for reasoning under uncertainty from noisy measurements, which prevent the over-fitting of data. The design of the underlying model facilitates the incorporation of prior knowledge and allows for an understanding of future events. However, a major disadvantage associated with BN modeling is that it requires large computational efforts to learn the underlying network structure. In many formulations learning a BN is an NP-hard problem, regardless of data size [63]. The number of different structures for a BN with n nodes, is given by the recursive formula

(1.9)

[62, 64]. As s(n) grows exponentially with n, learning the network structure by exhaustively searching over the space of all possible structures is infeasible even when n is small. Moreover, existence of equivalent networks presents obstacles in the inference of an optimal structure. BNs are inherently static in nature with no directed cycles. As a result, dynamic Bayesian networks (DBNs) have been developed to analyze time series data, which further pose computational challenges in structure learning. Thus, a tractable inference via BNs relies on suboptimal heuristic search algorithms. Some of the popular approaches include K2 [62] and MCMC [65], which have been implemented in the Bayes Net Tool Box [66].

1.4.1.4 Collaborative Graph Model

As opposed to gene expression data, the collaborative graph or cGraph model [17] utilizes gene sets to reconstruct the underlying network structure. It presents a simple model by employing a directed weighted graph to infer gene regulatory mechanisms.

Let V denote the set of all distinct genes among gene sets. In the underlying model for cGraph [17], the weight W_xy of an edge from a gene x to another gene y satisfies

(1.10)

and

(1.11)

Correspondingly, the weight matrix W can be interpreted as a transition probability matrix used in the theory of Markov chains. For network reconstruction, cGraph uses weighted counts of every pair of genes that appear among gene sets to approximate the weights of edges. Weight W_xy can be interpreted as P(y|x), which is the probability of randomly selecting a gene set S containing gene x followed by randomly choosing y as a second gene in the set. Assuming that both, the gene set containing gene x and y were chosen uniformly, weights are approximated as

(1.12)

Overall, cGraph is an inherently simple model, where a weighted edge measures the strength of a gene's connection with other genes. It is easy to understand, achievable at a manageable computational cost and appropriate for modeling pair wise relationships. However, cGraph adds a weighted edge between every pair of genes that appear together in some gene set and so the networks inferred by cGraph typically contain a large number of false positives and many interpretable functional modules.

1.4.1.5 Frequency Method

The frequency method presented in Ref. [18] reconstructs a directed network from a list of unordered gene sets. It estimates an ordering for each gene set by assuming

• tree structures in the paths corresponding to gene sets
• a prior availability of source and destination nodes in each gene set
• a prior availability of directed edges used to form a tree in each gene set, but not the order in which these edges appear in the tree.

Following the approach presented in Ref. [18], let us denote the set of source nodes, target nodes, and the collection of all directed edges involved in the network by S, T, and E, respectively. Each l S ∪ T ∪ E can be associated with a binary vector of length N by considering x_l(j) = 1, if l is involved with the jth gene set, where N is the total number of gene sets. Let s_j be the source and d_j be the destination node in the jth gene set. To estimate the order of genes in the jth gene set, FM identifies e^* satisfying

(1.13)

where the score λ_j(e) is defined as

(1.14)

for each e E with x_e(j) = 1. Note that λ_j(e) determines whether e is closer to s_j than it is to d_j. The edge e^* is placed closest to s_j. The edge corresponding to the next largest score follows e^*. The procedure is repeated until all edges are in order [18].

FM is computationally efficient and leads to a unique solution of the network inference problem. However, the model makes strong assumptions of the availability of source and target genes in each gene set as well as directed edges involved in the corresponding path. Considering the real-world scenarios, it is not practical to assume the availability of such gene set compendiums. The underlying assumptions in FM make it inherently deterministic in nature. Moreover, FM is subject to failure in the presence of multiple paths between the same pair of genes.

1.4.1.6 EM-Based Inference from Gene Sets

We now describe a more general approach from Refs. [19, 20] to network reconstruction from gene sets. It is termed as network inference from co-occurrences or NICO. Developed under the expectation–maximization (EM) framework, NICO infers the structure of the underlying network topology by assuming the order of genes in each gene set as missing information.

In NICO [19, 20], signaling pathways are viewed as a collection of T-independent samples of first-order Markov chain, denoted as

(1.15)

It is well known that Markov chain depends on an initial probability vector π and a transition matrix A. NICO treats the unobserved permutations {τ⁽¹⁾, . . ., τ^(T)} of {y⁽¹⁾, . . ., y^(T)} as hidden variables and computes the maximum-likelihood estimates of the parameters π and A via an EM algorithm. The E-step estimates expected permutations for each path conditioned on the current estimate of parameters, and the M-step updates the parameter estimates.

Let x^(m) denote a path with N_m elements. NICO models r_m as a random permutation matrix drawn uniformly from the collection of all permutations of N_m elements. In particular, the E-step computes the sufficient statistics

(1.16)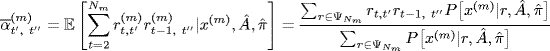

and

(1.17)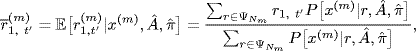

where is computed as

(1.18)

The M-step updates the parameters using the closed form expressions

(1.19)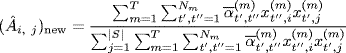

and

(1.20)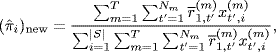

where |S| is the total number of distinct genes among gene sets. We refer to Refs. [19, 20], for additional theoretical details.

NICO presents an appealing approach to reconstruct the most likely signaling pathway from unordered gene sets. The mature EM framework provides a theoretical foundation for NICO. It is well known that gene expression data are often noisy and expensive. In order to infer the network topology, NICO purely relies on gene sets and does not require the corresponding gene expression measurements. As opposed to a single gene or a pair of genes, gene sets more naturally capture the higher-order interactions. These advantages make NICO a unique approach to infer signaling pathways directly from gene sets. However, NICO has a nontrivial computational complexity. For large networks, the combinatorial nature of the E-step makes the exact computation infeasible. Thus, an important sampling based approximation of the E-step has been proposed [19, 20]. Moreover, NICO assumes a linear arrangement of genes in each gene set without any feedback loops and so it is not applicable in real-world scenarios where signaling pathways are interconnected and regulated via feedback loops.

1.4.2 Reconstruction of Undirected Networks

1.4.2.1 Relevance Networks

Relevance networks [13] are based on measuring the strength of pairwise associations among genes from gene expression data. The pairwise association is measured in terms of Pearson's correlation coefficient. Given two genes x and y, Pearson's correlation coefficient is defined as

(1.21)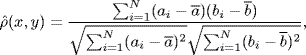

where x = (a₁, . . ., a_N) and y = (b₁, . . ., b_N) represent the N-dimensional observations for x and y with means and , respectively. There also exists an information theoretic version of RN's, where correlation is replaced with mutual information (MI) for each pair of genes. MI between x and y is defined as [12]

(1.22)

where E stands for the entropy of a gene expression pattern and is given by

(1.23)

For further readings on RN's, tools for their inference and comparison with other mutual information network inference approaches, we refer to Refs. [12,69–71].

In order to detect truly coexpressed gene pairs in an ad-hoc way, the calculated correlation values are compared with a predefined correlation cut-off value. If a calculated correlation value exceeds the cut-off value, the corresponding genes are connected by an undirected edge. We now present a more reliable two-stage approach from Ref. [32], which simultaneously controls the statistical and biological significance of the inferred network. We only consider the case of Pearson's correlation, however, the method can be extended to the case of Kendall correlation coefficient and partial correlation coefficients [32]. Assuming a total of M genes, we simultaneously test Λ = pairs of two-sided hypotheses

(1.24)

for each i, j = 1, . . ., M and i ≠ j. Here, S is the measure of strength of co-expression (Pearson's correlation in this case) between gene pairs and cor_min is the minimum acceptable strength of coexpression. The sample correlation coefficient ( in this case) serves as a decision statistic to decide the pairwise dependency of two genes. For large sample size N, the per comparison error rate (PCER) p-values for pairwise correlation is computed as

(1.25)

where Φ is the cumulative density function of a standard Gaussian random variable. The above expression is derived from an asymptotic Gaussian approximations to . Note that the PCER p-value refers to the probability of type I error rate which is incurred in hypothesis testing for one pair of gene at a time. To simultaneously test a total of Λ hypotheses, the following FDR-based procedure is used. It guarantees that FDR associated with hypotheses testing is not larger than α.

For a fixed FDR level α and cor_min, the procedure consists of the following two stages.

• In Stage I, the null hypothesis

• Let us assume a total of Λ₁ gene pairs cross Stage I. In Stage II, asymptotic PCER confidence intervals I^λ(α) are constructed for each value of S corresponding to Λ₁ pairs. These intervals are then converted into FDR confidence intervals using the formula I^λ(α) → I^λ(Λ₁α/Λ) [73]. For the case of Pearson's correlation, let 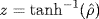. Then the intervals I^λ(α), for Λ₁ true Pearson's correlation coefficients ρ, are given by Ref. [32]

RNs offer a simple and computationally efficient approach to infer undirected biological networks. However, RNs only infer a possible functional relevancy between gene pairs and not necessarily their direct association. A high correlation value may result from an indirect association, for example, regulation of a pair of genes by another gene. Thus, RNs are often dense with many interpretable functional modules. Limitations of RNs have been studied in Refs. [69, 71].

1.4.2.2 Graphical Gaussian Models

To overcome the shortcomings of RNs, Gaussian graphical models [1–3] were introduced to measure the strength of direct pairwise associations. In GGMs, gene associations are quantified in terms of partial correlations. Indeed, marginal correlation measures a composite correlation between a pair of genes that includes the effects of all other genes in the network, whereas partial correlation measures the strength of direct correlation excluding the effects of all other genes.

In GGMs [1, 2], it is assumed that data are drawn from a multivariate normal distribution N(μ, Σ). The partial correlation matrix Π is computed from the inverse Ω = (ω_ij) = Σ⁻¹ of the covariance matrix as

(1.28)

Calculation of partial correlation matrix is followed by statistical tests, which determine the strength of partial correlation computed for every pair of genes. Significantly nonzero entries in the estimated partial correlation matrix are used to reconstruct the underlying network.

However, the above method is applicable only if the sample size (N) is larger than the number of genes (p) in the given data set, for otherwise the sample covariance matrix cannot be inverted. To tackle the case of small N and large p, a shrinkage covariance estimator has been developed [3], which guarantees the positive definiteness of the estimated covariance matrix and thus leads to its invertibility. The shrinkage estimator is written as a convex combination of the following two estimators:

• unconstrained estimator 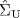of the covariance matrix, which often has a high variance
• constrained estimator 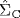of the covariance matrix, which has a certain bias but a low variance.

This is expressed as

(1.29)

where λ [0 1] represents the shrinkage parameter. The Ledoit–Wolf lemma [74] is used to estimate an optimal value of λ which minimizes the expected value of mean square error. Let A = [a_ij] and B = [b_ij] denote empirical covariance and correlation matrices, respectively. Then is given by [3]

(1.30)

where

(1.31)

and

(1.32)

For the list of constrained estimators and computation of , we refer to Ref. [3]. Overall, GGM is an appealing approach for the reverse engineering of undirected biological networks. It is theoretically sound, easy to understand and computationally efficient. GGM is particularly suitable to tackle low throughput data, where the number of samples is much larger than the number of variables. For high throughput molecular profiling data, the distribution-free shrinkage estimator guarantees to estimate an invertible covariance matrix. However, an edge in a network reconstructed via GGM only represents a possible functional relationship between corresponding genes without any indication of gene regulatory mechanisms.

Reconstruction of biological networks is fundamental in understanding the origin of various biological phenomenon. The computational approaches presented above play a crucial role in achieving this goal. However, the complexity arising due to a large number of variables and many hypothetical connections introduces further challenges in gaining biological insights from a reconstructed network. It is necessary to uncover the structural arrangement of a large biological network by identifying tightly connected zones of the network representing functional modules. In the following section, we present some popular network partitioning algorithms, which allow us to infer the biomolecular mechanisms at the level of subnetworks.