2.13 Centrality

In the previous sections, we explained the global features of complex networks, such as the degree distribution and average shortest path length. However, it is also important to characterize local properties (i.e., the characteristics of each node in a complex network). For example, the clustering coefficient indicates the degree of clustering among the neighbors of a node, as explained in Section 2.6.1. In addition to the clustering coefficient, centrality is an important concept in network analysis because it helps in finding central (important) nodes in complex networks.

2.13.1 Definition

To date, several node centralities have been proposed, based on topological information. Well-used centralities are as follows.

Degree Centrality

The degree centrality [48] is the simplest centrality measure. Assuming a correlation between the centrality (or importance) of node i and the degree of node i (k_i), the degree centrality of node i is defined as

(2.49)

where N is the network size (i.e., the total number of nodes). Since this centrality is essentially similar to the node degree, this is widely used in network analysis.

Closeness Centrality

The closeness centrality [48] is based on the shortest path length between nodes i and j, d(i, j). When the average path length between a node and the other nodes is relatively short, the centrality of such a node may be high. On the basis of this interpretation, the centrality of node i is expressed as

(2.50)

However, we cannot appropriately calculate the closeness centrality when there are isolated components resulting from unreachable node pairs. We need to assume a connected network to obtain the closeness centrality.

Betweenness Centrality

As in the case of closeness centrality, the betweenness centrality [48] is based on the shortest path between nodes. However, the interpretation of centrality is a little different in these two cases.

The betweenness centrality focuses on the number of visits through the shortest paths. If a walker moves from one node to another node via the shortest path, then the nodes with a large number of visits by the walker may have high centrality. The betweenness centrality of node i is defined as

(2.51)

where σ_st(i) and σ_st are, respectively, the number of shortest paths between nodes s and t, on which node i is located, and the number of shortest paths between nodes s and t. For normalization, the betweenness centrality is finally divided by the maximum value.

The calculation of betweenness centrality assumes a connected component, as in closeness centrality, because the betweenness centrality is also based on the shortest paths.

Eigenvector Centrality

The eigenvector centrality is a higher version of degree centrality. The degree centrality is only based on the number of neighbors. However, the eigenvector centrality can consider the centralities of neighbors. Let C_E(i) be the centrality of node i; C_E(i) is proportional to the average of the centralities of the neighbors of node i,

(2.52)

where M_ij is an adjacency matrix. M_ij = 1 if node i connects to node j, and M_ij = 0 otherwise. λ is a constant. Suppose that x = (C_E(1), . . ., C_E(N)); this equation is rewritten as λ.x = M · x. The eigenvector centrality is defined as the eigenvector with the largest eigenvalue [49].

2.13.2 Comparison of Centrality Measures

As mentioned in the previous section, the interpretation of centrality is different in these different centrality measures. To explain the differences between the centrality measures, we show an application example (Fig. 2.14).

Figure 2.14 Comparison of centrality measures. The numerical values and lowercase letters located near nodes indicate centrality values and node identifiers, respectively. The size of a node is based on its centrality value normalized by the maximum centrality value.

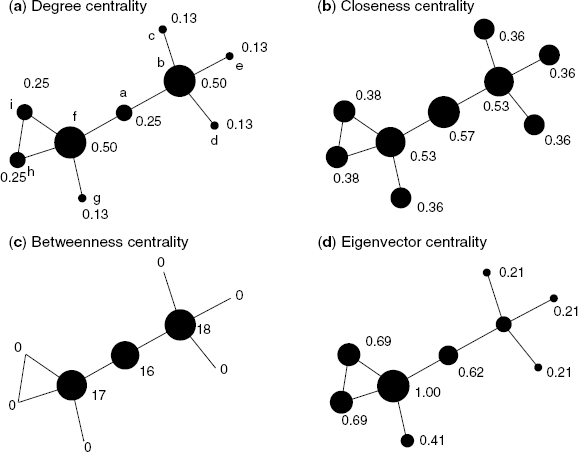
Since the degree centrality is based on the node degree, high-degree nodes (e.g., nodes b and f) show high centrality. By contrast, however, node a also has high centrality in the case of both closeness centrality and betweeness centrality, although its degree is low (k_a = 2). Node a plays the role of an intersection between two subnetworks whose node sets are {b, c, d, e} and {f, g, h, i}, respectively. Thus, node a may be interpreted as a central node with respect to the role of intersection. These centrality measures can find an important node because they are based on the shortest path analysis.

The results for eigenvector centrality are similar to those for degree centrality because eigenvector centrality is an extended degree centrality. In general, however, we observe high eigenvector centrality for nodes belonging to a dense subgraph (i.e., cliques) because the eigenvector centrality is determined by the centralities of its neighbors in addition to its own centrality. As shown in Figure 2.14d, the nodes belonging to the triangle consisting of nodes f, h, and i show high centralities.

In this manner, these centrality measures provide different interpretations of node centrality. In the light of these difference, we need to use centrality measures carefully.