3.3 Modeling Without Parameter Tuning: A Case Study of Metabolic Networks

In the previous section, we introduced a simple model for reproducing several structural properties observed in real-world biological networks. Furthermore, this model network shows good qualitative and quantitative agreement with real data.

For model fitting, we need to tune model parameters. The parameters may be estimated by minimizing the difference between the model and real data using statistical methods. However, the optimal solutions may require substantial calculation, after which multiple optimal solutions may be obtained. Furthermore, the possibility of trivial agreements (e.g., over-fittings) may remain if the model has several tunable parameters.

In order to avoid this problem, we need to eliminate parameter tunings and construct models in which parameters are determined from observable statistics obtained from real-network data, such as the number of nodes.

In this chapter, we focus on metabolic networks and introduce a network model without parameter tuning.

3.3.1 Network Model

Here, we consider metabolic networks in which nodes and edges represent metabolites and metabolic reactions (substrate–product relationships based on atomic tracing [26]) and propose a simple model that reproduces the structural properties of metabolic networks with two parameters, p and q. These parameters are determined from the statistics of real data (see Section 3.3.3 for details).

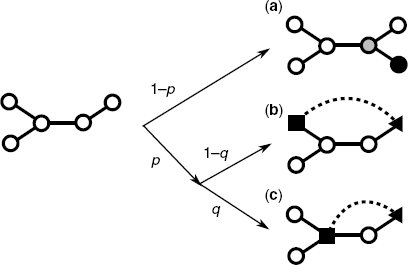
In general, it is believed that metabolic networks evolve by a reaction (enzyme) gain due to evolutionary events (see Ref. 27 for details). In this case, we can consider two situations: the case that a new reaction occurs between a new metabolite and an existing metabolite (Event I) and the case that a new reaction occurs between existing metabolites (Event II).

With the above consideration, the modeling is as follows.

Figure 3.9 Schematic diagram of the growth mechanisms of the model. (a) Event I. The black and gray nodes represent a new node and a randomly selected existing node, respectively. (b) and (c) Event II. The dashed lines correspond to new edges. The triangular nodes are randomly selected existing nodes. The quadrangular nodes are existing nodes, selected by a random walk from each red node. The new edge becomes a short-cut path between the triangular node and the quadrangular node.

3.3.2 Analytical Solution

Degree Distribution. First, we show the analytical solution for degree distribution of the model via mean-field-based analysis [12,22].

We consider the time evolution of k_i, which is the degree of node i. When Event I occurs, the degree of node i increases by one with the probability 1/N, where N is the total number of nodes. Further, when Event II occurs, two existing nodes are selected and their respective degrees increase. The degree of one node increases by one with the probability 1/N, because this node is randomly selected. The degree of another node increases by one with the probability k_i/∑ _jk_j, because this node is selected by a random walk from a randomly selected node. It is reported that the probability that a walker arrives at this node equals k_i/∑ _jk_j, irrespective of the number of steps in the random walk [28]. Note that this probability equals to that of the preferential attachment. Thus, the time evolution of k_i is

(3.17)

where N = (1 − p)t, because the number of nodes increases by one with the probability 1 − p, and ∑_jk_j = 2t because one edge is added each time. It should be noted that this equation is independent of the bypassed path length (the parameter q). The solution of the above equation with the initial condition k_i(t = s) = 1 is

(3.18)

where A(p) = 2/[p(1 − p)].

From the above equation, because s/t = P(≥ k) as shown in the previous section, the cumulative distribution P(≥ k) is

(3.19)

Since , we finally obtain the degree distribution

(3.20)

where the degree exponent γ is

(3.21)

As shown in Equation 3.20, the degree distribution follows a power law with a cutoff within a small degree.

Degree-Dependent Clustering Coefficient. Next, we show an analytical solution for the degree-dependent clustering coefficient of the model via mean-field-based analysis.

The clustering coefficient of node i is defined as C_i = 2M_i/[k_i(k_i − 1]), where M_i is the number of edges among the neighbors of node i. We consider the time evolution of M_i. The number of edges of M_i increases with the probability pq, because M_i increases when Event II occurs and a path of length 2 is bypassed (a triangle is generated). In other words, we do not need to consider a bypassed path with length greater than or equal to 3. Next, the M_i of each node, which belongs to the triangle, approximately increases by one. The M_i of one node increases by one with the probability 1/N, because this node is selected at random. The M_is of the other two nodes increase by one with the probability k_i/∑ _jk_j, because these nodes are selected by a random walk. Therefore, the time evolution of M_i is

(3.22)

where N = (1 − p)t and ∑_jk_j = 2t. Moreover, k_i = [A(p) + 1](t/s)^p/2 − A(p), as shown in Equation 3.18.

The solution of the above equation with the initial condition M_i(t = s) = 0 is

(3.23)

where A(p) = 2/[p(1 − p)]. From Equation 3.18, since k_i = [A(p) + 1](t/s)^p/2 − A(p), this equation is rewritten as

(3.24)

Substituting this equation into the definition of clustering coefficient described above, we finally obtain the degree-dependent clustering coefficient

(3.25)

Average Clustering Coefficient. Finally, we show an analytical solution for the average clustering coefficient of the model.

The average clustering coefficient is expressed as the summation of the product of the degree distribution and the degree-dependent clustering coefficient: , where K_m is the maximum degree. We approximate this summation by the integral equation:

(3.26)

The maximum degree indicates that the cumulative probability equals to 1/N; thus, P(≥ K_m) = 1/N. From Equation 3.19, K_m can be expressed as

(3.27)

Equation 3.26 is solved via numerical integration because it is analytically unsolvable.

3.3.3 Estimation of the Parameters

As explained in Section 3.3.1, this model has two parameters p and q. In order to reproduce the structural properties of metabolic networks, we need to estimate these parameters in real-world networks. In this section, we discuss the approach for estimating these parameters.

3.3.4 Comparison with Real Data

Here, we compare structural properties of this model with those of real metabolic networks.

First, we obtain the parameters p and q from the metabolic network of each organism using Equations 3.28 and 3.31, respectively. Substituting the parameters into the equations, shown in Section 3.3.2, we obtain the structural properties predicted from this model.

Figure 3.10 shows a comparison between the degree distribution of our model and that of real metabolic networks. We provide the P(k) values of two well-known organisms.

Figure 3.10 Comparison between the degree distribution of our model and that of real metabolic networks of E. coli (a) and Bacillus subtilis (b). The symbols represent the data for real networks. The lines are obtained from Equation 3.20.

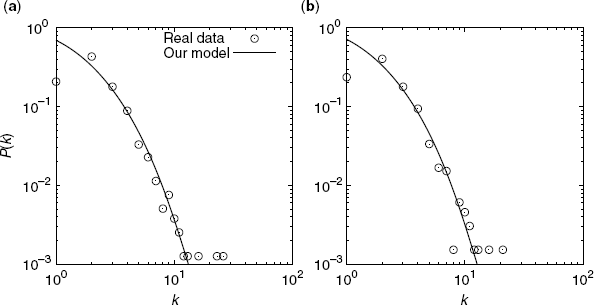
Figure 3.11 shows a comparison between the degree exponent of our model and that of real metabolic networks. For comparison, the degree exponents are obtained by the maximum likelihood method, considering a cutoff, represented by A(p), as follows:

(3.32)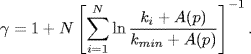

This value is different from that obtained by the original maximum likelihood method [29].

Figure 3.11 Comparison between the degree exponent γ of our model (theoretical) and that of real metabolic networks (real). The dashed line represents γ_real = γ_theory.

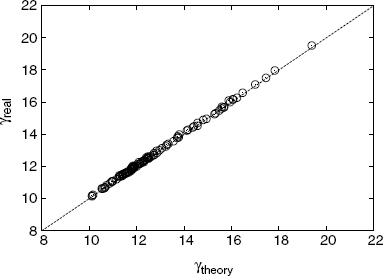
Figure 3.12 shows a comparison between the degree-dependent clustering coefficient of our model and that of real metabolic networks. We show C(k) for the same two organisms.

Figure 3.12 Comparison of the degree-dependent clustering coefficient between our model and the real metabolic networks of (a) E. coli and (b) B. subtilis. The symbols indicate the data for real networks. The lines are obtained from Equation 3.25.

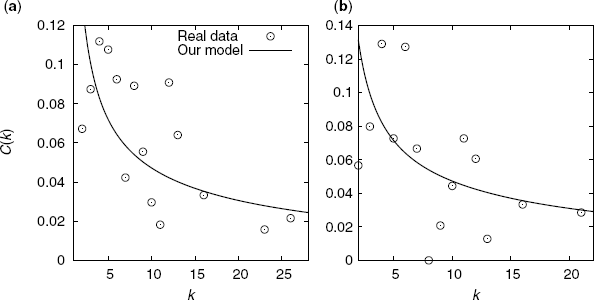
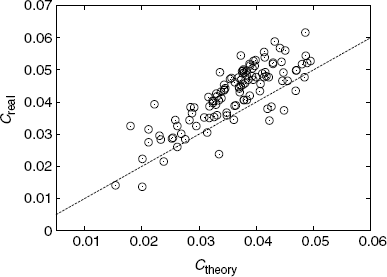
Figure 3.13 shows a comparison between the average clustering coefficient of our model and that of real metabolic networks. The predicted average clustering coefficients are obtained with Equation 3.26 via numerical integration.

Figure 3.13 Comparison between the average clustering coefficient C of our model (theoretical) and that of real metabolic networks (real). The dashed line shows C_real = C_theory.

As shown in Figures 3.10–3.13, the theoretical predictions are in good agreement with the real data, indicating that this model can reproduce the structural properties of real metabolic networks.

As mentioned above, this model has a few parameters, which can be estimated very easily. Furthermore, the model parameters relate to the frequency of evolutionary events such as horizontal gene transfers and gene duplications, through which the metabolic networks expand (e.g., see Refs. [30,31]). This model may be useful for the estimation of missing pathways and the evolutionary origin of metabolic reactions.