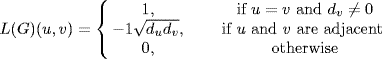6.2 Weighted Spectral Distribution

We now derive our metric, the weighted spectral distribution, relating it to another common structural metric, the clustering coefficient, before showing how it characterizes networks with different mixing properties.

Denote an undirected graph as G = (V, E) where V is the set of vertices (nodes) and E is the set of edges (links). The adjacency matrix of G, A(G), has an entry of one if two nodes, u and , are connected and zero otherwise

(6.1)

Let be the degree of node and D = diag(sum(A)) be the diagonal matrix having the sum of degrees for each node (column of matrix) along its main diagonal. Denoting by I the identity matrix (I)_i,j = 1 if i = j, 0 otherwise, the normalized Laplacian L associated with graph G is constructed from A by normalizing the entries of A by the node degrees of A as

(6.2)

or equivalently

(6.3)

As L is a real symmetric matrix there is an orthonormal basis of real eigenvectors e₀, . . ., e_n−1 (i.e., , and ) with associated eigenvalues λ₀, . . ., λ_n−1. It is convenient to label these so that λ₀ ≤ . . . ≤ λ_n−1. The set of pairs (eigenvectors and eigenvalues of L) is called the spectrum of the graph. It can be seen that

(6.4)

The eigenvalues λ₀, . . ., λ_n−1 represent the strength of projection of the matrix onto the basis elements. This may be viewed from a statistical point of view [3] where each may be used to approximate A(G) with approximation error inversely proportional to 1 − λ_i. However, for a graph, those nodes which are best approximated by in fact form a cluster of nodes. This is the basis for spectral clustering, a technique which uses the eigenvectors of L to perform clustering of a dataset or graph [4]. The first (smallest) nonzero eigenvalue and associated eigenvector are associated with the main clusters of data. Subsequent eigenvalues and eigenvectors can be associated with cluster splitting and also identification of smaller clusters [5]. Typically, there exists what is called a spectral gap in which for some k and j, λ_k λ_k+1 ≈ 1 ≈ λ_j−1 λ_j. That is, eigenvalues λ_k+1, . . ., λ_j−1¹ are approximately equal to one and are likely to represent links in a graph which do not belong to any particular cluster. It is then usual to reduce the dimensionality of the data using an approximation based on the spectral decomposition. However, in this chapter we are interested in representing the global structure of a graph (e.g., we are interested in the presence or absence of many small clusters), which is essentially the spread of clustering across the graph. This information is contained in all the eigenvalues of the spectral decomposition.

Let x = (x₀, . . ., x_n−1) be a vector. From Equation (6.3) we see that

(6.5)

Now, the eigenvalues cannot be large because from Equation (6.5) we obtain

(6.6)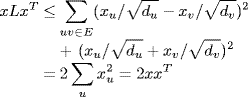

and so . What is more, the mean of the eigenvalues is 1 because

(6.7)

by Equation (6.3), where tr(L) is the trace of L.

To summarize, the eigenvalues of L lie in the range 0–2 (the smallest being 0), that is, 0 = λ₀ ≤ . . . ≤ λ_n−1 ≤ 2, and their mean is 1.

The distribution of the n numbers λ₀, . . ., λ_n−1 contains useful information about the network, as will be seen. In turn, information about this distribution is given by its moments in the statistical sense, where the N th moment is 1/n ∑ _i(1 − λ_i)^N. These moments have a direct physical interpretation in terms of the network, as follows. Writing B for the matrix D^−1/2AD^−1/2, so that L = I − B, then by Equation (6.3) the entries of B are given by

(6.8)

Now the numbers 1 − λ_i are the eigenvalues of B = I − L, and so ∑_i(1 − λ_i)^N is just tr(B^N). Writing b_i,j for the (i, j)th entry of B, the (i, j)th entry of B^N is the sum of all products where i₀ = i and i_N = j. But b_i,j, as given by Equation (6.8), is zero unless nodes i and j are adjacent. So we define an N-cycle in G to be a sequence of vertices u₁u₂ . . . u_N with u_i adjacent to u_i+1 for i = 1, . . ., N − 1 and with u_N adjacent to u₁. (Thus, for example, a triangle in G with vertices set {a, b, c} gives rise to six 3-cycles abc, acb, bca, bac, cab, and cba. Note that, in general, an N-cycle might have repeated vertices.) We now have

(6.9)

the sum being over all N-cycles C = u₁u₂ . . . u_N in G. Therefore, ∑_i(1 − λ_i)^N counts the number of N-cycles, normalized by the degree of each node in the cycle.

The number of N-cycles is related to various graph properties. The number of 2-cycles is just (twice) the number of edges and the number of 3-cycles is (six times) the number of triangles. Hence, ∑_i(1 − λ)³ is related to the clustering coefficient, as discussed below. An important graph property is the number of 4-cycles. A graph which has the minimum number of 4-cycles, for a graph of its density, is quasirandom, that is, it shares many of the properties of random graphs, including, typically, high connectivity, low diameter, having edges distributed uniformly through the graph, and so on. This statement is made precise in Refs. [6] and [7]. For regular graphs Equation (6.7) shows that the sum ∑_i(1 − λ)⁴ is directly related to the number of 4-cycles. In general, the sum counts the 4-cycles with weights, for the relationship between the sum and the quasirandomness of the graph in the nonregular case, see the more detailed discussion in Ref. [8], Chapter 5]. The right-hand side of Equa-tion (6.9) can also be seen in terms of random walks. A random walk starting at a vertex with degree d_u will choose an edge with probability 1/d_u and at the next vertex, say , choose an edge with probability , and so on. Thus, the probability of starting and ending randomly at a vertex after N steps is the sum of the probabilities of all N-cycles that start and end at that vertex. In other words exactly the right-hand side of Equation (6.9). As pointed out in Ref. [9], random walks are an integral part of the Internet AS structure.

The left-hand side of Equation (6.9) provides an interesting insight into graph structure. The right-hand side is the sum of normalized N-cycles whereas the left-hand side involves the spectral decomposition. We note in particular that the spectral gap is diminished because eigenvalues close to one are given a very low weighting compared to eigenvalues far from one. This is important as the eigenvalues in the spectral gap typically represent links in the network that do not belong to any specific cluster and are not therefore important parts of the larger structure of the network.

Next, we consider the well-known clustering coefficient. It should be noted that there is little connection between the clustering coefficient, and cluster identification, referred to above. The clustering coefficient, γ(G), is defined as the average number of triangles divided by the total number of possible triangles

(6.10)

where T_i is the number of triangles for node i and d_i is the degree of node i. Now consider a specific triangle between nodes a, b, and c. For the clustering coefficient, noting that the triangle will be considered three times, once from each node, the contribution to the average is

(6.11)

However, for the weighted spectrum (with N = 3), this particular triangle gives rise to six 3-cycles and contributes

(6.12)

So, it can be seen that the clustering coefficient normalizes each triangle according to the total number of possible triangles while the weighted spectrum (with N = 3) instead normalizes using a product of the degrees. Thus, the two metrics can be considered to be similar but not equal. Indeed, it should be noted that the clustering coefficient is in fact not a metric in the strict sense. While two networks can have the same clustering coefficient they may differ significantly in structure. In contrast, the elements of ∑_i(1 − λ)³ will only agree if two networks are isomorphic.

We now formally define the weighted spectrum as the normalized sum of N-cycles as

(6.13)

However, calculating the eigenvalues of a large (even sparse) matrix is computationally expensive. In addition, the aim here is to represent the global structure of a graph and so precise estimates of all the eigenvalue values are not required. Thus, the distribution² of eigenvalues is sufficient. In this chapter, the distribution of eigenvalues f(λ = k) is estimated using pivoting and Sylvester's Law of Inertia to compute the number of eigenvalues that fall in a given interval. To estimate the distribution, we use K equally spaced bins.³ A measure of the graph can then be constructed by considering the distribution of the eigenvalues as

(6.14)

where the elements of ω(G, N) form the weighted spectral distribution

(6.15)

In addition, a metric can then be constructed from ω(G) for comparing two graphs, G₁ and G₂, as

(6.16)

where f₁ and f₂ are the eigenvalue distributions of G₁ and G₂ and the distribution of eigenvalues is estimated in the set K of bins [0, 2]. Equation (6.16) satisfies all the properties of a metric [10].

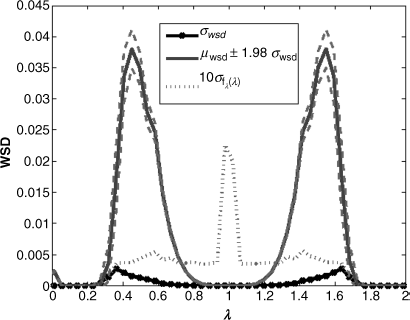
We next wish to test if the WSD for graphs generated by the same underlying process vary significantly (to show that the WSD is stable). To do this, we generate a set of graphs that have very similar structure and test to see if their WSDs are also similar. The results of an empirical test are shown in Figure 6.1. This plot was created by generating 50 topologies using the AB [11] generator with the (fixed) optimum parameters determined in Section 6.6, but with different initial conditions.⁴ For each run the spectral and weighted spectral distributions are recorded yielding 50 × 50 bin values which are then used to estimate standard deviations. As the underlying model (i.e., the AB generator) is the same for each run, the structure might be expected to remain the same and so a “structural metric” should be insensitive to random initial conditions. As can be seen the standard deviation⁵ of the (unweighted) spectrum, , is significantly higher at the center of the spectrum. However, for the WSD, the standard deviation, σ_wsd, peaks at the same point as the WSD; the noise in the spectral gap has been suppressed. The evidence suggests that the WSD successfully filters out the noise around 1 in the middle region and highlights the important parts of the signal.

Figure 6.1 Mean and standard deviations for WSD and (unweighted) spectrum for the AB model over 50 simulations.