8.11 Summary and Conclusions

Graph kernels allow the utilization of graph theory in a formal framework suitable for kernel-based machine learning. They have the advantage that they can potentially exploit information not available to vector-based representations alone. In many application domains, graphs are a natural representation of input data, for example, the molecular structure graph in cheminformatics. On the downside, most graph kernels are computationally demanding, with cubic or higher degree runtimes. This prevents them from being used with large graphs. They are not always interpretable, although this depends highly on the kernel.

What makes a good graph kernel? Borgwardt and Kriegel [33] have argued that a graph kernel “should be (i) a good measure of graph similarity, (ii) computable in polynomial time, (iii) positive definite, and (iv) applicable to all graphs, not just a small subset of graphs.” While (i), (ii), (iii) are reasonable requirements, with (i) being somewhat vague, I disagree with (iv). From basic considerations (Section 8.1.3), a graph kernel is a trade-off between completeness (expressivity) and complexity (runtime). A kernel that exploits characteristics of specific graph classes (e.g., graphs with bounded vertex degrees, such as molecular structure graphs) can take advantage of these characteristics to achieve a better trade-off on this graph class. Restriction to a specific graph class is a way to introduce domain knowledge; it is also related to the principle stated by Vapnik [104] that “when solving a problem of interest, do not solve a more general problem as an intermediate step.”

Many graph kernels count particular types of subgraphs (the features), such as walks, paths, trees, cyclic patterns, or fixed-size subgraphs. Only counting subgraphs ignores their relative position in the graph, information that can be crucial in some application domains.

Some graph kernels, for example, random walk kernels and substructure-based kernels, rely on comparing all possible subgraphs, for example, all random walks, or all subtrees of a certain type. It has been argued [46] that this might negatively affect performance due to the combinatorial growth of the number of such subgraphs, most of which will not be related with the target property. Proposed solutions include downweighting of the contribution of larger subgraphs, prior knowledge-based selection of relevant subgraphs, or, considering contextual information for limited-size subgraphs [45].

Graph kernels often use other kernels to compare vertex or edge labels, such as the Dirac kernel (also Kronecker kernel, k(x, x ') = 1 if x = x ', and 0 otherwise). This simple approach works surprisingly well, but might reduce expressivity, and more sophisticated label comparisons might prove beneficial, depending on the application.

Certain graph kernels support only edge labels. An edge kernel can be extended to include information from a vertex kernel via

(8.26)

Many theoretical properties of graph kernels have not been sufficiently investigated, for example, completeness (Section 8.1.3). It has been shown [58] that even approximating a complete graph kernel is NP-hard. This result, however, is for general graphs; it is not clear whether it holds for specialized graph classes. The related graph isomorphism problem, for example, is in P for bounded degree graphs [105].

Graph kernels have some interesting connections to other topics, for example, random walk kernels are a special case of rational kernels on weighted transducers [64], and shortest path kernels are a generalization of the Wiener index [1,106].

Further guidance is necessary with regard to the conditions under which it is advantageous to use a graph kernel, and as to which graph kernel to use. Intuitively, one should consider graph kernels when there is a natural representation of inputs as graphs. If several graph kernels match all application requirements such as the use of vertex or edge labels, one should choose the kernel that most closely matches the specialized graph class of the application. Besides that, it is suggested to try different graph kernels, possibly in combination with vector-based representations, for example, via multiple kernel learning [107].

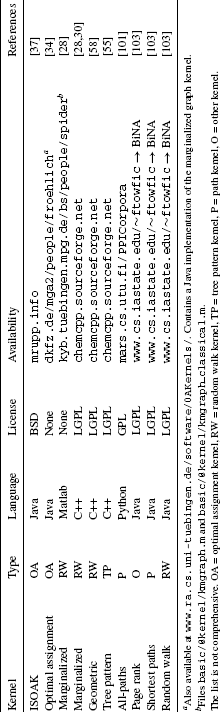
Table 8.4 lists several available implementations of graph kernels. It is intended to provide a starting point for scientists who want to apply graph kernels in their own research. Compared to the available machine learning software (see, e.g., www.mloss.org), the number of readily available graph kernel implementations is rather limited.

Table 8.4 Implementations of Graph Kernels.

Graph kernels constitute a promising and relatively new approach in kernel-based machine learning and its applications. A growing number of retrospective validation studies attests to their potential usefulness, often reaching or surpassing state-of-the-art performance, but application studies are still lacking. In my opinion, research in the following directions would be most useful to exploit graph kernels further: (i) the conduction of prospective application studies, (ii) the development of graph kernels (or the adaptation of existing ones) that take advantage of domain-specific graph characteristics, such as the bounded vertex degree of molecular structure graphs, (iii) investigations of theoretical graph kernel properties. In addition, an increase in available graph kernel implementations would be of great practical benefit.