Abstract

An infinite series expansion is given for the bivariate normal cumulative distribution function. This expansion converges as a series of powers of , where ρ is the correlation coefficient, and thus represents a good alternative to the tetrachoric series when ρ is large in absolute value.

Introduction

The cumulative normal distribution function

with

appears frequently in modern finance: Essentially all explicit equations of options pricing, starting with the Black-Scholes formula, involve this function in one form or another. Increasingly, however, there is also a need for the bivariate cumulative normal distribution function

1

where the bivariate normal density is given by

2

This need arises in at least the following areas:

1. Pricing exotic options. Options with payout depending on the prices of two lognormally distributed assets, or two normally distributed factors, involve the bivariate normal distribution function in the pricing formula. Examples include the so-called rainbow options (such as calls on maximum or minimum of two assets), extendible options, and spread and cross-country swaps.
2. Correlations of derivatives. While the instantaneous correlation of two derivatives is the same as the correlation of the underlying assets, calculation of the correlation over noninfinitesimal intervals often requires the bivariate normal function.
3. Loan loss correlations. If a loan default occurs when the borrower's assets fall below a certain point, the covariance of defaults on two loans is given by a bivariate normal formula. This covariance is needed when evaluating the variance of loan portfolio losses.

A standard procedure for calculating the bivariate normal distribution function is the tetrachoric series,

3

where

are the Hermite polynomials. For a comprehensive review of the literature, see Gupta (1963).

The tetrachoric series (3) converges only slightly faster than a geometric series with quotient ρ, and it is therefore not very practical to use when ρ is large in absolute value. In this note, we give an alternative series that converges approximately as a geometric series with quotient .

The Expansion

The starting point of this chapter is the formula

4

which is proven in the Appendix.

Because of the identity

for , we can limit ourselves to calculation of . Suppose first that . Then by integrating Equation (4) with from ρ to 1 we get

5

where

To evaluate the integral, substitute

to obtain

6

Using the expansion

we get

7

Because

8

for and , the series in Equation (7) converges uniformly in the interval and can be integrated term by term. It can be easily established that

for . Substitution into (7) then gives

9

where

10

Equations (5), (9), and (10) give an infinite series expansion for with . When , integration of Equation (4) from –1 to ρ yields

11

with Q still given by (9) and (10).

A convenient procedure for computing the terms in the expansion (9) is using the recursive relationships

with

To determine the speed of convergence of (9), integrate the first half of inequality (8) from 0 to . This results in the bound

for , and therefore the series (9) converges approximately as . As the tetrachoric series for ,

12

converges approximately as , a reasonable method for calculating is to use the tetrachoric series (12) when and expressions (5) and (11) with the series (9) when .

The error in the calculation of resulting from using m terms in the expansion (9) is bound in absolute value by

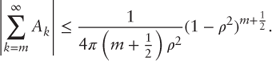
Numerical Results

A comparison of the convergence of the tetrachoric series (12) and the alternative calculations (5) or (11) with the series (9) in calculating for high values of the correlation coefficient is given in Tables 33.1 and 2.

Number of Terms	Tetrachoric	Alternative	Tetrachoric	Alternative
1	.171033	.158632	.174894	.158655
2	.171033	.158631	.174894	.158655
3	.167298	.158631	.170304	.158655
5	.161764	.158631	.162651	.158655
10	.157961	.158631	.156068	.158655
20	.158466	.158631	.158068	.158655
30	.158660	.158631	.159374	.158655
50	.158632	.158631	. 158599	.158655
100	.158631	.158631	.158711	.158655
200	.158631	.158631	.158657	.158655
300	.158631	.158631	.158654	.158655
Exact	.158631		.158655

	ρ = .8	ρ = .9	ρ = .95	ρ = .99
Tetrachoric series
	8	16	30	121
	7	14	22	75
	6	11	18	42
Alternative series
	4	3	2	1
	3	1	1	1
	1	1	1	1

Appendix

We prove equation (4) by stating a slightly more general result. Let

and

be the p-variate normal density function and cumulative distribution function, respectively, where is a vector and is a symmetric positive-definite matrix. We now prove the following lemma:

Lemma. Let . Then for

Here is the vector of is the vector of the remaining components of x, and are the , and decompositions of Σ into the i-th and j-th row and column and the remaining rows and columns.

Proof. We have

Define by and put . Since for

where E_ij is the matrix having unity for the (i,j)-th element and zeros elsewhere, we get on substitution

On the other hand,

and

and therefore

Integrating with respect to and exchanging the order of integration and differentiation yields the first equality of the lemma. The second equality follows from the factorization

References

1. Gupta, S.S. (1963). “Probability Integrals of Multivariate Normal and Multivariate t.” Annals of Mathematical Statistics, 34, 792–828.
2. Johnson, N.L., and S. Kotz. (1972). Distributions in Statistics: Continuous Multivariate Distributions. New York: John Wiley & Sons.
3. Vasicek, O.A. (1997). “The Loan Loss Distribution.” Working paper, KMV Corporation.