11
Financial Applications
In this chapter, we discuss several financial applications of GARCH models. In connecting these models with those frequently used in mathematical finance, one is faced with the problem that the latter are generally written in continuous time. We start by studying the relation between GARCH and continuous‐time processes. We present sufficient conditions for a sequence of stochastic difference equations to converge in distribution to a stochastic differential equation (SDE) as the length of the discrete time intervals between observations goes to zero. We then apply these results to GARCH(1,1)‐type models. The second part of this chapter is devoted to the pricing of derivatives. We introduce the notion of stochastic discount factor (SDF) and show how it can be used in the GARCH framework. The final part of the chapter is devoted to risk measurement.
11.1 Relation Between GARCH and Continuous‐Time Models
Continuous‐time models are central to mathematical finance. Most theoretical results on derivative pricing rely on continuous‐time processes, obtained as solutions of diffusion equations. However, discrete‐time models are the most widely used in applications. The literature on discrete‐time models and that on continuous‐time models was developed independently, but it is possible to establish connections between the two approaches.
11.1.1 Some Properties of Stochastic Differential Equations
This first section reviews the basic material from diffusion processes, which will be known to many readers. In some probability space ![]() , a
d
‐dimensional process {W
t
; 0 ≤ t < ∞} is called standard Brownian motion if
W
0 = 0 almost surely, for
s ≤ t
, the increment
W
t
− W
s
is independent of
σ{W
u
; u ≤ s} and is
, a
d
‐dimensional process {W
t
; 0 ≤ t < ∞} is called standard Brownian motion if
W
0 = 0 almost surely, for
s ≤ t
, the increment
W
t
− W
s
is independent of
σ{W
u
; u ≤ s} and is ![]() distributed, where
I
d
is the
d × d
identity matrix. Brownian motion is a Gaussian process and admits a version with continuous paths.
distributed, where
I
d
is the
d × d
identity matrix. Brownian motion is a Gaussian process and admits a version with continuous paths.
A SDE in ℝ p is an equation of the form
where x 0 ∈ ℝ p , μ and σ are measurable functions, defined on ℝ p and, respectively, taking values in ℝ p and ℳ p × d , the space of p × d matrices. Here, we only consider time‐homogeneous SDEs, in which the functions μ and σ do not depend on t . A process (X t ) t ∈ [0, T] is a solution of this equation, and is called a diffusion process, if it satisfies
Existence and uniqueness of a solution require additional conditions on the functions μ and σ . The simplest conditions require Lipschitz and sublinearity properties:

where t ∈ [0, + ∞ [, x, y ∈ ℝ p , and K is a positive constant. In these inequalities, ‖ · ‖ denotes a norm on either ℝ p or ℳ p × d . These hypotheses also ensure the ‘non‐explosion’ of the solution on every time interval of the form [0, T ] with T > 0 (see Karatzas and Shreve 1988, Theorem 5.2.9). They can be considerably weakened, in particular when p = d = 1. The term μ(X t ) is called the drift of the diffusion, and the term σ(X t ) is called the volatility. They have the following interpretation:
These relations can be generalised using the second‐order differential operator defined, in the case p = d = 1, by
Indeed, for a class of twice continuously differentiable functions f , we have
Moreover, the following property holds: if φ is a twice continuously differentiable function with compact support, then the process
is a martingale with respect to the filtration (F t ), where F t is the σ ‐field generated by {W s , s ≤ t}. This result admits a reciprocal which provides a useful characterisation of diffusions. Indeed, it can be shown that if, for a process (X t ), the process (Y t ) just defined is a F t ‐martingale, for a class of sufficiently smooth functions φ , then (X t ) is a diffusion and solves Eq. (11.1).
Stationary Distribution
In certain cases, the solution of an SDE admits a stationary distribution, but in general, this distribution is not available in explicit form. Wong (1964) showed that, for model ( 11.1) in the univariate case ( p = d = 1) with σ(·) ≥ 0, if there exists a function f that solves the equation
and belongs to the Pearson family of distributions, that is, of the form
where a < − 1 and b < 0, then Eq. ( 11.1) admits a stationary solution with density f .
11.1.2 Convergence of Markov Chains to Diffusions
Consider a Markov chain ![]() with values in ℝ
d
, indexed by the time unit
τ > 0. We transform
Z
(τ)
into a continuous‐time process,
with values in ℝ
d
, indexed by the time unit
τ > 0. We transform
Z
(τ)
into a continuous‐time process, ![]() , by means of the time interpolation
, by means of the time interpolation
Under conditions given in the next theorem, the process ![]() converges in distribution to a diffusion. Denote by ‖·‖ the Euclidean norm on ℝ
d
.
converges in distribution to a diffusion. Denote by ‖·‖ the Euclidean norm on ℝ
d
.
Euler Discretisation of a Diffusion
Diffusion processes do not admit an exact discretisation in general. An exception is the geometric Brownian motion, defined as a solution of the real SDE
where μ and σ are constants. It can be shown that if the initial value x 0 is strictly positive, then X t ∈ (0, ∞) for any t > 0. By Itô's lemma, 2 we obtain
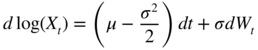
and then, by integration of this equation between times kτ and (k + 1)τ , we get the discretised version of model (11.12),

For general diffusions, an explicit discretised model does not exist, but a natural approximation, called the Euler discretisation, is obtained by replacing the differential elements by increments. The Euler discretisation of the SDE ( 11.1) is then given, for the time unit τ , by
The Euler discretisation of a diffusion converges in distribution to this diffusion (Exercise 11.2).
Convergence of GARCH‐M Processes to Diffusions
It is natural to assume that the return of a financial asset increases with risk. Economic agents who are risk‐averse must receive compensation when they own risky assets. ARMA‐GARCH type time series models do not take this requirement into account because the conditional mean and variance are modelled separately. A simple way to model the dependence between the average return and risk is to specify the conditional mean of the returns in the form
where
ξ
and
λ
are parameters. By doing so we obtain, when ![]() is specified as an ARCH, a particular case of the ARCH in mean (ARCH‐M) model, introduced by Engle, Lilien, and Robins (1987). The parameter
λ
can be interpreted as the price of risk and can thus be assumed to be positive. Other specifications of the conditional mean are obviously possible. In this section, we focus on a GARCH(1, 1)‐M model of the form
is specified as an ARCH, a particular case of the ARCH in mean (ARCH‐M) model, introduced by Engle, Lilien, and Robins (1987). The parameter
λ
can be interpreted as the price of risk and can thus be assumed to be positive. Other specifications of the conditional mean are obviously possible. In this section, we focus on a GARCH(1, 1)‐M model of the form
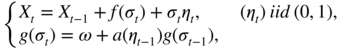
where ω > 0, f is a continuous function from ℝ+ to ℝ, g is a continuous one‐to‐one map from ℝ+ to itself and a is a positive function. The previous interpretation implies that f is increasing, but at this point, it is not necessary to make this assumption. When g(x) = x 2 and a(x) = αx 2 + β with α ≥ 0, β ≥ 0, we get the classical GARCH(1, 1) model. Asymmetric effects can be introduced, for instance by taking g(x) = x and a(x) = α + x + − α − x − + β , with x + = max(x, 0), x − = min(x, 0), α + ≥ 0, α − ≥ 0, β ≥ 0.
Observe that the constraint for the existence of a strictly stationary and non‐anticipative solution (Y t ), with Y t = X t − X t − 1 , is written as
by the techniques studied in Chapter 2.
Now, in view of the Euler discretisation (11.15), we introduce the sequence of models indexed by the time unit τ , defined by

for
k > 0, with initial values ![]() ,
, ![]() and assuming
and assuming ![]() The introduction of a delay
k
in the second equation is due to the fact that
σ
(k + 1)τ
belongs to the
σ
‐field generated by
η
kτ
and its past values.
The introduction of a delay
k
in the second equation is due to the fact that
σ
(k + 1)τ
belongs to the
σ
‐field generated by
η
kτ
and its past values.
Noting that the pair Z kτ = (X (k − 1)τ , g(σ kτ )) defines a Markov chain, we obtain its limiting distribution by application of Theorem 11.1. We have, for z = (x, g(σ)),
This latter quantity converges if
where ω and δ are constants.
Similarly,
which converges if and only if
where ζ is a positive constant. Finally,

converges if and only if
where ρ is a constant such that ρ 2 ≤ ζ .
Under these conditions, we thus have

Moreover, we have

We are now in a position to state our next result.
11.2 Option Pricing
Classical option pricing models rely on independent Gaussian returns processes. These assumptions are incompatible with the empirical properties of prices, as we saw, in particular, in Chapter 1. It is thus natural to consider pricing models founded on more realistic, GARCH‐type, or stochastic volatility, price dynamics.
We start by briefly recalling the terminology and basic concepts related to the Black–Scholes model. Appropriate financial references are provided at the end of this chapter.
11.2.1 Derivatives and Options
The need to hedge against several types of risks gave rise to a number of financial assets called derivatives. A derivative (derivative security or contingent claim) is a financial asset whose payoff depends on the price process of an underlying asset: action, portfolio, stock index, currency, etc. The definition of this payoff is settled in a contract.
There are two basic types of option. A call option (put option) or more simply a call (put) is a derivative giving to the holder the right, but not the obligation, to buy (sell) an agreed quantity of the underlying asset S , from the seller of the option on (or before) the expiration date T , for a specified price K , the strike price or exercise price. The seller (or ‘writer’) of a call is obliged to sell the underlying asset should the buyer so decide. The buyer pays a fee, called a premium, for this right. The most common options, since their introduction in 1973, are the European options, which can be exercised only at the option expiry date, and the American options, which can be exercised at any time during the life of the option. For a European call option, the buyer receives, at the expiry date, the amount max(S T − K, 0) = (S T − K)+ since the option will not be exercised unless it is ‘in the money’. Similarly, for a put, the payoff at time T is (K − S T )+ . Asset pricing involves determining the option price at time t . In what follows, we shall only consider European options.
11.2.2 The Black–Scholes Approach
Consider a market with two assets, an underlying asset, and a risk‐free asset. The Black and Scholes (1973) model assumes that the price of the underlying asset is driven by a geometric Brownian motion
where μ and σ are constants and (W t ) is a standard Brownian motion. The risk‐free interest rate r is assumed to be constant. By Itô's lemma, we obtain

showing that the logarithm of the price follows a generalised Brownian motion, with drift μ − σ 2/2 and constant volatility. Integrating the two sides of Equality (11.32) between times t − 1 and t yields the discretised version

The assumption of constant volatility is obviously unrealistic. However, this model allows for explicit formulas for option prices, or more generally for any derivative based on the underlying asset S , with payoff g(S T ) at the expiry date T . The price of this product at time t is unique under certain regularity conditions 3 and is denoted by C(S, t) for simplicity. The set of conditions ensuring the uniqueness of the derivative price is referred to as the complete market hypothesis. In particular, these conditions imply the absence of arbitrage opportunities, that is, that there is no ‘free lunch’. It can be shown 4 that the derivative price is
where the expectation is computed under the probability π corresponding to the equation
where ![]() denotes a standard Brownian motion. The probability
π
is called the risk‐neutral probability, because under
π
the expected return of the underlying asset is the risk‐free interest rate
r
. It is important to distinguish this from the historic probability, that is, the law under which the data are generated (here defined by model (11.31)). Under the risk‐neutral probability, the price process is still a geometric Brownian motion, with the same volatility
σ
but with drift
r
. Note that the initial drift term,
μ
, does not play a role in the pricing formula (11.34). Moreover, the actualised price
X
t
= e
−rt
S
t
satisfies
denotes a standard Brownian motion. The probability
π
is called the risk‐neutral probability, because under
π
the expected return of the underlying asset is the risk‐free interest rate
r
. It is important to distinguish this from the historic probability, that is, the law under which the data are generated (here defined by model (11.31)). Under the risk‐neutral probability, the price process is still a geometric Brownian motion, with the same volatility
σ
but with drift
r
. Note that the initial drift term,
μ
, does not play a role in the pricing formula (11.34). Moreover, the actualised price
X
t
= e
−rt
S
t
satisfies ![]() . This implies that the actualised price is a martingale for the risk‐neutral probability:
e
−r(T − t)
E
π
[S
T
∣ S
t
] = S
t
. Note that this formula is obvious in view of Relation ( 11.34), by considering the underlying asset as a product with payoff
S
T
at time
T
.
. This implies that the actualised price is a martingale for the risk‐neutral probability:
e
−r(T − t)
E
π
[S
T
∣ S
t
] = S
t
. Note that this formula is obvious in view of Relation ( 11.34), by considering the underlying asset as a product with payoff
S
T
at time
T
.
The Black–Scholes formula is an explicit version of ( 11.34) when the derivative is a call, that is, when g(S T ) = (K − S T )+ , given by
where Φ is the conditional distribution function (cdf) of the ![]() distribution and
distribution and

In particular, it can be seen that if
S
t
is large compared to
K
, we have ![]() , and the call price is approximately given by
S
t
− e
−rτ
K
, that is, the current underlying price minus the actualised exercise price. The price of a put
P(S, t) follows from the put–call parity relationship (Exercise 11.4):
C(S, t) = P(S, t) + S
t
− e
−rτ
K
.
, and the call price is approximately given by
S
t
− e
−rτ
K
, that is, the current underlying price minus the actualised exercise price. The price of a put
P(S, t) follows from the put–call parity relationship (Exercise 11.4):
C(S, t) = P(S, t) + S
t
− e
−rτ
K
.
A simple computation (Exercise 11.5) shows that the European call option price is an increasing function of S t , which is intuitive. The derivative of C(S, t) with respect to S t , called delta, is used in the construction of a riskless hedge, a portfolio obtained from the risk‐free and risky assets allowing the seller of a call to cover the risk of a loss when the option is exercised. The construction of a riskless hedge is often referred to as delta hedging.
The previous approach can be extended to other price processes, in particular if (S t ) is solution of a SDE of the form
under regularity assumptions on μ and σ . When the geometric Brownian motion for S t is replaced by another dynamics, the complete market property is generally lost. 5
11.2.3 Historic Volatility and Implied Volatilities
Note that, from a statistical point of view, the sole unknown parameter in the Black–Scholes pricing formula (11.36) is the volatility of the underlying asset. Assuming that the prices follow a geometric Brownian motion, application of this formula thus requires estimating
σ
. Any estimate of
σ
based on a history of prices
S
0, …, S
n
is referred to as historic volatility. For geometric Brownian motion, the log‐returns log(S
t
/S
t − 1) are, by ( 11.32), iid ![]() distributed variables. Several estimation methods for
σ
can be considered, such as the method of moments and the maximum likelihood method (Exercise 11.7). An estimator of
C(S, t) is then obtained by replacing
σ
by its estimate.
distributed variables. Several estimation methods for
σ
can be considered, such as the method of moments and the maximum likelihood method (Exercise 11.7). An estimator of
C(S, t) is then obtained by replacing
σ
by its estimate.
Another approach involves using option prices. In practice, traders usually work with the so‐called implied volatilities. These are the volatilities implied by option prices observed in the market. Consider a European call option whose price at time
t
is ![]() . If
. If ![]() denotes the price of the underlying asset at time
t
, an implied volatility
denotes the price of the underlying asset at time
t
, an implied volatility ![]() is defined by solving the equation
is defined by solving the equation

This equation cannot be solved analytically, and numerical procedures are called for. Note that the solution is unique because the call price is an increasing function of σ (Exercise 11.8).
If the assumptions of the Black–Scholes model, that is, the geometric Brownian motion, are satisfied, implied volatilities calculated from options with different characteristics, but the same underlying asset should coincide with the theoretical volatility σ . In practice, implied volatilities calculated with different strikes or expiration dates are very unstable, which is not surprising since we know that the geometric Brownian motion is a misspecified model.
11.2.4 Option Pricing when the Underlying Process is a GARCH
In discrete time, with time unit δ , the binomial model (in which, given S t , S t + δ can only take two values) allows us to define a unique risk‐neutral probability, under which the actualised price is a martingale. This model is used, in the Cox, Ross, and Rubinstein (1979) approach, as an analog in discrete time of the geometric Brownian motion. Intuitively, the assumption of a complete market is satisfied (in the binomial model as well as in the Black–Scholes model) because the number of assets, two, coincides with the number of states of the world at each date. Apart from this simple situation, the complete market property is generally lost in discrete time. It follows that a multiplicity of probability measures may exist, under which the prices are martingales, and consequently, a multiplicity of pricing formulas such as ( 11.34). Roughly speaking, there is too much variability in prices between consecutive dates.
To determine options prices in incomplete markets, additional assumptions can be made on the risk premium and/or the preferences of the agents. A modern alternative relies on the concept of SDF, which allows pricing formulas in discrete time similar to those in continuous time to be obtained.
Stochastic Discount Factor
We start by considering a general setting. Suppose that we observe a vector process Z = (Z t ) and let I t denote the information available at time t , that is, the σ ‐field generated by {Z s , s ≤ t}. We are interested in the pricing of a derivative whose payoff is g = g(Z T ) at time T . Suppose that there exists, at time t < T , a price C t (Z, g, T) for this asset. It can be shown that, under mild assumptions on the function g ↦ C t (Z, g, T), 6 we have the representation
The variable M t, T is called the SDF for the period [t, T]. The SDF introduced in representation (11.37) is not unique and can be parameterised. The formula applies, in particular, to the zero‐coupon bond of expiry date T , defined as the asset with payoff 1 at time T . Its price at t is the conditional expectation of the SDF,
It follows that Relation ( 11.37) can be written as

Forward Risk‐Neutral Probability
Observe that the ratio
M
t, T
/B(t, T) is positive and that its mean, conditional on
I
t
, is 1. Consequently, a probability change removing this factor in formula (11.38) can be done.
7
Denoting by
π
t, T
, the new probability and by ![]() the expectation under this probability, we obtain the pricing formula
the expectation under this probability, we obtain the pricing formula
The probability law π t, T is called forward risk‐neutral probability. Note the analogy between this formula and Relation ( 11.34), the latter corresponding to a particular form of B(t, T). To make this formula operational, it remains to specify the SDF.
Risk‐Neutral Probability
As mentioned earlier, the SDF is not unique in incomplete markets. A natural restriction, referred to as a temporal coherence restriction, is given by
On the other hand, the one‐step SDFs are constrained by
where S t ∈ I t is the price of an underlying asset (or a vector of assets). We have

Noting that

we can make a change of probability such that the SDF vanishes. Under a probability law ![]() , called risk‐neutral probability, we thus have
, called risk‐neutral probability, we thus have

The risk‐neutral probability satisfies the temporal coherence property: ![]() is related to
is related to ![]() through the factor
M
T, T + 1/B(T, T + 1). Without the restriction (11.40), the risk‐neutral forward probability does not satisfy this property.
through the factor
M
T, T + 1/B(T, T + 1). Without the restriction (11.40), the risk‐neutral forward probability does not satisfy this property.
Pricing Formulas
One approach to deriving pricing formulas is to specify, parametrically, the dynamics of Z t and of M t, t + 1 , taking the constraint (11.41) into account.
Now consider a general GARCH‐type model of the form

where μ t and σ t belong to the σ ‐field generated by the past of Z t , with σ t > 0. Suppose that the σ ‐fields generated by the past of ε t , Z t , and η t are the same, and denote this σ ‐field by I t − 1 . Suppose again that B(t, t + 1) = e −r . Consider for the SDF an affine exponential specification with random coefficients, given by
where a t , b t ∈ I t . The constraints ( 11.41) are written as

that is, after simplification,
As before, these equations provide a unique solution (a t , b t ). The risk‐neutral probability π t, t + 1 is defined through the characteristic function

The last two equalities are obtained by taking into account the constraints on a t and b t . Thus, under the probability π t, t + 1 , the law of the process (Z t ) is given by the model

The independence of the ![]() follows from the independence between
follows from the independence between ![]() and
I
t
(because
and
I
t
(because ![]() has a fixed distribution conditional on
I
t
) and from the fact that
has a fixed distribution conditional on
I
t
) and from the fact that ![]()
The model under the risk‐neutral probability is then a GARCH‐type model if the variable ![]() is a measurable function of the past of
is a measurable function of the past of ![]() . This generally does not hold because the relation
. This generally does not hold because the relation
entails that the past of ![]() is included in the past of ε
t
, but not the reverse.
is included in the past of ε
t
, but not the reverse.
If the relation (11.48) is invertible, in the sense that there exists a measurable function
f
such that ![]() , model (11.47) is of the GARCH type, but the volatility
, model (11.47) is of the GARCH type, but the volatility ![]() can take a very complicated form as a function of the
can take a very complicated form as a function of the ![]() . Specifically, if the volatility under the historic probability is that of a classical GARCH(1, 1), we have
. Specifically, if the volatility under the historic probability is that of a classical GARCH(1, 1), we have

Finally, using π t, T , the forward risk‐neutral probability for the expiry date T , the price of a derivative is given by the formula
or, under the historic probability, in view of the temporal coherence restriction ( 11.40),
It is important to note that, with the affine exponential specification of the SDF, the volatilities coincide with the two probability measures. This will not be the case for other SDFs (Exercise 11.11).
Numerical Pricing of Option Prices
Explicit computation of the expectation involved in Formula (11.49) is not possible, but the expectation can be evaluated by simulation. Note that, under π t, T , S T , and S t are linked by the formula

where ![]() . At time
t
, suppose that an estimate
. At time
t
, suppose that an estimate ![]() of the coefficients of model (11.51) is available, obtained from observations
S
1, …, S
t
of the underlying asset. Simulated values
of the coefficients of model (11.51) is available, obtained from observations
S
1, …, S
t
of the underlying asset. Simulated values ![]() of
S
T
, and thus simulated values
of
S
T
, and thus simulated values ![]() of
Z
T
, for
i = 1, …, N
, are obtained by simulating, at step
i
,
T − t
independent realisations
of
Z
T
, for
i = 1, …, N
, are obtained by simulating, at step
i
,
T − t
independent realisations ![]() of the
of the ![]() and by setting
and by setting

where the ![]() , are recursively computed from
, are recursively computed from
taking, for instance, as initial value ![]() , the volatility estimated from the initial GARCH model (this volatility being computed recursively, and the effect of the initialisation being negligible for
t
large enough under stationarity assumptions). This choice can be justified by noting that for SDFs of the form (11.45), the volatilities coincide under the historic and risk‐neutral probabilities. Finally, a simulation of the derivative price is obtained by taking
, the volatility estimated from the initial GARCH model (this volatility being computed recursively, and the effect of the initialisation being negligible for
t
large enough under stationarity assumptions). This choice can be justified by noting that for SDFs of the form (11.45), the volatilities coincide under the historic and risk‐neutral probabilities. Finally, a simulation of the derivative price is obtained by taking

The previous approach can obviously be extended to more general GARCH models, with larger orders and/or different volatility specifications. It can also be extended to other SDFs.
Empirical studies show that, comparing the computed prices with actual prices observed on the market, GARCH option pricing provides much better results than the classical Black–Scholes approach (see, for instance, Sabbatini and Linton 1998; Härdle and Hafner 2000).
To conclude this section, we observe that the formula providing the theoretical option prices can also be used to estimate the parameters of the underlying process, using observed options (see, for instance, Hsieh and Ritchken 2005).
11.3 Value at Risk and Other Risk Measures
Risk measurement is becoming more and more important in the financial risk management of banks and other institutions involved in financial markets. The need to quantify risk typically arises when a financial institution has to determine the amount of capital to hold as a protection against unexpected losses. In fact, risk measurement is concerned with all types of risks encountered in finance. Market risk, the best‐known type of risk, is the risk of change in the value of a financial position. Credit risk, also a very important type of risk, is the risk of not receiving repayments on outstanding loans, as a result of borrower's default. Operational risk, which has received more and more attention in recent years, is the risk of losses resulting from failed internal processes, people, and systems, or external events. Liquidity risk occurs when, due to a lack of marketability, an investment cannot be bought or sold quickly enough to prevent a loss. Model risk can be defined as the risk due to the use of a misspecified model for the risk measurement.
The need for risk measurement has increased dramatically, in the last two decades, due to the introduction of new regulation procedures. In 1996, the Basel Committee on Banking Supervision (a committee established by the central bank governors in 1974) prescribed a so‐called standardised model for market risk. At the same time, the Committee allowed the larger financial institutions to develop their own internal model. The second Basel Accord (Basel II), initiated in 2001, considers operational risk as a new risk class and prescribes the use of finer approaches to assess the risk of credit portfolios. By using sophisticated approaches, the banks may reduce the amount of regulatory capital (the capital required to support the risk), but in the event of frequent losses, a larger amount may be imposed by the regulator. Parallel developments took place in the insurance sector, giving rise to the Solvency projects. In response to the financial crisis of 2008, the third Basel accord, whose first measures started in 2013, strengthened the regulation and risk managment of banks, in particular by introducing a liquidity coverage ratio.
A risk measure that is used for specifying capital requirements can be thought of as the amount of capital that must be added to a position to make its risk acceptable to regulators. Value at risk (VaR) is arguably the most widely used risk measure in financial institutions. In 1993, the business bank JP Morgan publicised its estimation method, RiskMetrics, for the VaR of a portfolio. VaR is now an indispensable tool for banks, regulators, and portfolio managers. We start by defining VaR and discussing its properties.
11.3.1 Value at Risk
Definition
VaR is concerned with the possible loss of a portfolio in a given time horizon. A natural risk measure is the maximum possible loss. However, in most models, the support of the loss distribution is unbounded so that the maximum loss is infinite. The concept of VaR replaces the maximum loss by a maximum loss which is not exceeded with a given (high) probability.
VaR should be computed using the predictive distribution of future losses, that is the conditional distribution of future losses using the current information. However, for horizons h > 1, this conditional distribution may be hard to obtain.
To be more specific, consider a portfolio whose value at time t is a random variable denoted V t . At horizon h , the loss is denoted
The distribution of L t, t + h is called the loss distribution (conditional or not). This distribution is used to compute the regulatory capital which allows certain risks to be covered, but not all of them. In general, V t is specified as a function of d unobservable risk factors.
The distribution of −L t,t + h conditional on the available information at time t is called the profit and loss (P&L) distribution.
The determination of reserves depends on
- the portfolio,
- the available information at time t and the horizon h , 8
- a level α ∈ (0, 1) characterising the acceptable risk. 9
Denote by R t, h (α) the level of the reserves. Including these reserves, which are not subject to remuneration, the value of the portfolio at time t + h becomes V t + h + R t, h (α). The capital used to support risk, the VaR, also includes the current portfolio value,
and satisfies
where P t is the probability conditional on the information available at time t . 10 VaR can thus be interpreted as the capital exposed to risk in the event of bankruptcy. Equivalently,
In probabilistic terms, VaR t, h (α) is thus simply the (1 − α)‐quantile of the conditional loss distribution. If, for instance, for a confidence level 99% and a horizon of 10 days, the VaR of a portfolio is €5000, this means that, if the composition of the portfolio does not change, there is a probability of 1% that the potential loss over 10 days will be larger than €5000.
In particular, it is obvious that VaR t, h (α) is a decreasing function of α .
From Definition (11.53), computing a VaR simply reduces to determining a quantile of the conditional loss distribution. Figure 11.1 compares the VaR of three distributions, with the same variance but different tail thicknesses. The thickest tail, proportional to 1/x
4
, is that of the Student
t
distribution with 3 degrees of freedom, here denoted as ![]() ; the thinnest tail, proportional to
; the thinnest tail, proportional to ![]() , is that of the Gaussian
, is that of the Gaussian ![]() ; and the double exponential ℰ possesses a tail of intermediate size, proportional to
; and the double exponential ℰ possesses a tail of intermediate size, proportional to ![]() . For some very small level
α
, the VaRs are ranked in the order suggested by the thickness of the tails:
. For some very small level
α
, the VaRs are ranked in the order suggested by the thickness of the tails: ![]() . However, Figure 11.1b shows that this ranking does not hold for the standard levels
α = 1% or 5%.
. However, Figure 11.1b shows that this ranking does not hold for the standard levels
α = 1% or 5%.

Figure 11.1
(a) VaR is the (1 − α)‐quantile of the conditional loss distribution. (b) VaR as a function of
α ∈ [1% , 5%] for a Gaussian distribution  (solid line), a Student
t
distribution with 3 degrees of freedom
(solid line), a Student
t
distribution with 3 degrees of freedom  (dashed line) and a double exponential distribution ℰ (thin dotted line). The three laws are standardised so as to have unit variances. For
α = 1%, we have
(dashed line) and a double exponential distribution ℰ (thin dotted line). The three laws are standardised so as to have unit variances. For
α = 1%, we have  , whereas for
α = 5%, we have
, whereas for
α = 5%, we have  .
.
VaR and Conditional Moments
Let us introduce the first two moments of L t, t + h conditional on the information available at time t :
Suppose that
where ![]() is a random variable with cumulative distribution function
F
h
. Denote by
is a random variable with cumulative distribution function
F
h
. Denote by ![]() the quantile function of the variable
the quantile function of the variable ![]() , defined as the generalised inverse of
F
h
:
, defined as the generalised inverse of
F
h
:
If
F
h
is continuous and strictly increasing, we simply have ![]() , where
, where ![]() is the ordinary inverse of
F
h
. In view of the relations ( 11.53) and (11.54), it follows that
is the ordinary inverse of
F
h
. In view of the relations ( 11.53) and (11.54), it follows that

Consequently,
VaR can thus be decomposed into an ‘expected loss’ m t, t + h , the conditional mean of the loss, and an ‘unexpected loss’ σ t, t + h F ←(1 − α), also called economic capital.
The apparent simplicity of formula (11.55) masks difficulties in (i) deriving the first conditional moments for a given model, and (ii) determining the law F h , supposedly independent of t , of the standardised loss at horizon h .
Consider the price of a portfolio, defined as a combination of the prices of d assets, p t = a ′ P t , where a, P t ∈ ℝ d . Introducing the price variations ΔP t = P t − P t − 1 , we have

The term structure of the VaR, that is its evolution as a function of the horizon, can be analysed in different cases.
It is often more convenient to work with the log‐returns r t = Δ1 log p t , assumed to be stationary, than with the price variations. Letting q t (h, α) be the α ‐quantile of the conditional distribution of the future returns r t + 1 + … + r t + h , we obtain (Exercise 11.15)
Non Subadditivity of VaR
VaR is often criticised for not satisfying, for any distribution of the price variations, the ‘subadditivity’ property. Subadditivity means that the VaR for two portfolios after they have been merged should be no greater than the sum of their VaRs before they were merged. However, this property does not hold: if L 1 and L 2 are two loss variables, we do not necessarily have, in obvious notation,
The lack of subadditivity of the VaR is often interpreted negatively as this does not encourage diversification. Note however that, as underlined by the previous example, the distribution of an average of non integrable iid variables can be more dispersed than the common distribution of the individual variables. In such an extreme situation, diversification does not reduce risk, and any good risk measure should be overadditive, as it is the case for the VaR.
11.3.2 Other Risk Measures
Even if VaR is the most widely used risk measure, the choice of an adequate risk measure is an open issue. As already seen, the convexity property, with respect to the portfolio composition, is not satisfied for VaR with some distributions of the loss variable. In what follows, we present several alternatives to VaR, together with a conceptualisation of the ‘expected’ properties of risks measures.
Volatility and Moments
In the Markowitz (1952) portfolio theory, the variance is used as a risk measure. It might then seem natural, in a dynamic framework, to use the volatility as a risk measure. However, volatility does not take into account the signs of the differences from the conditional mean. More importantly, this measure does not satisfy some ‘coherency’ properties, as will be seen later (translation invariance, subadditivity).
Expected Shortfall
The expected shortfall (ES), or anticipated loss, is the standard risk measure used in insurance since Solvency II. This risk measure is closely related to VaR, but avoids certain of its conceptual difficulties. It is more sensitive than VaR to the shape of the conditional loss distribution in the tail of the distribution. In contrast to VaR, it is informative about the expected loss when a big loss occurs.
Let
L
t, t + h
be such that ![]() . In this section, the conditional distribution of
L
t, t + h
is assumed to have a continuous and strictly increasing cdf. The ES at level
α
, also referred to as Tailvar, is defined as the conditional expectation of the loss given that the loss exceeds the VaR:
. In this section, the conditional distribution of
L
t, t + h
is assumed to have a continuous and strictly increasing cdf. The ES at level
α
, also referred to as Tailvar, is defined as the conditional expectation of the loss given that the loss exceeds the VaR:
We have
Now P t [L t, t + h > VaR t, h (α)] = 1 − P t [L t, t + h ≤ VaR t, h (α)] = 1 − (1 − α) = α , where the last but one equality follows from the continuity of the cdf at VaR t, h (α). Thus
The following characterisation also holds (Exercise 11.16):
ES thus can be interpreted, for a given level α , as the mean of the VaR over all levels u ≤ α. Obviously, ES t, h (α) ≥ VaR t, h (α).
Note that the integral representation makes ES t, h (α) a continuous function of α , whatever the distribution (continuous or not) of the loss variable. VaR does not satisfy this property (for loss variables which have a zero mass over certain intervals).
More generally, we have under assumption ( 11.54), in view of Expressions (11.64) and ( 11.55),
Distortion Risk Measures
Continue to assume that the cdf F of the loss distribution is continuous and strictly increasing. For notational simplicity, we omit the indices t and h . From Definition ( 11.64), the ES is written as

where the term ![]() can be interpreted as the density of the uniform distribution over [0, α]. More generally, a
distortion risk measure
(DRM) is defined as a number
can be interpreted as the density of the uniform distribution over [0, α]. More generally, a
distortion risk measure
(DRM) is defined as a number

where G is a cdf on [0,1], called distortion function, and F is the loss distribution. The introduction of a probability distribution on the confidence levels is often interpreted in terms of optimism or pessimism. If G admits a density g which is increasing on [0,1], that is, if G is convex, the weight of the quantile F −1(1 − u) increases with u : large risks receive small weights with this choice of G . Conversely, if g decreases, those large risks receive the bigger weights.
VaR at level α is a DRM, obtained by taking for G the Dirac mass at α . As we have seen, the ES corresponds to the constant density g on [0, α]: it is simply an average over all levels below α.
A family of DRMs is obtained by parameterising the distortion measure as

where the parameter p reflects the confidence level, that is the degree of optimism in the face of risk.
Coherent Risk Measures
In response to criticisms of VaR, several notions of coherent risk measures have been introduced. One of the proposed definitions is the following.
This definition has the following immediate consequences:
- ρ(0) = 0, using the homogeneity property with L = 0. More generally, ρ(c) = c for all constants c (if a loss of amount c is certain, a cash amount c should be added to the portfolio).
- If L ≥ 0, then ρ(L) ≥ 0. If a loss is certain, an amount of capital must be added to the position.
- ρ(L − ρ(L)) = 0, that is the deterministic amount ρ(L) cancels the risk of L .
These requirements, which are controversial (see Example 11.10), are not satisfied for most risk measures used in finance. The variance, or more generally any risk measure based on the centred moments of the loss distribution, does not satisfy the monotonicity property, for instance. The expectation can be seen as a coherent, but uninteresting, risk measure. VaR satisfies all conditions except subadditivity: we have seen that this property holds for (dependent or independent) Gaussian variables, but not for general variables. ES is a coherent risk measure in the sense of Definition 11.2 (Exercise 11.17). It can be shown (see Wang and Dhaene 1998) that DRMs with G concave satisfy the subadditivity requirement. Note that, because finite expectation is required, ES and DRMs do not apply to fat tailed distributions such as the Pareto distributions of Example 11.10, for which overaddidivity is desirable.
11.3.3 Estimation Methods
Unconditional VaR
The simplest estimation method is based on the
K
last returns at horizon
h
, that is,
r
t + h − i
(h) =log(p
t + h − i
/p
t − i
), for
i = h…, h + K − 1. These
K
returns are viewed as scenarios for future returns. The non‐parametric historical VaR is simply obtained by replacing
q
t
(h, α) in Relation (11.60) by the empirical
α
‐quantile of the last
K
returns. Typical values are
K = 250 and
α = 1%, which means that the third worst return is used as the empirical quantile. A parametric version is obtained by fitting a particular distribution to the returns, for example a Gaussian ![]() which amounts to replacing
q
t
(h, α) by
which amounts to replacing
q
t
(h, α) by ![]() , where
, where ![]() and
and ![]() are the estimated mean and standard deviation. Apart from the (somewhat unrealistic) case where the returns are iid, these methods have little theoretical justification.
are the estimated mean and standard deviation. Apart from the (somewhat unrealistic) case where the returns are iid, these methods have little theoretical justification.
RiskMetrics Model
A popular estimation method for the conditional VaR relies on the RiskMetrics model. This model is defined by the equations

where
λ ∈ ]0, 1[ is a smoothing parameter, for which, according to RiskMetrics (Longerstaey 1996), a reasonable choice is
λ = 0.94 for daily series. Thus, ![]() is simply the prediction of
is simply the prediction of ![]() obtained by simple exponential smoothing. This model can also be viewed as an IGARCH(1, 1) without intercept. It is worth noting that no non‐degenerate solution (r
t
)
t ∈ ℤ
to Model (11.66) exists (Exercise 11.18). Thus Model (11.66) is not a realistic data generating process for any usual financial series. This model can, however, be used as a simple tool for VaR computation. From Relation ( 11.60), we get
obtained by simple exponential smoothing. This model can also be viewed as an IGARCH(1, 1) without intercept. It is worth noting that no non‐degenerate solution (r
t
)
t ∈ ℤ
to Model (11.66) exists (Exercise 11.18). Thus Model (11.66) is not a realistic data generating process for any usual financial series. This model can, however, be used as a simple tool for VaR computation. From Relation ( 11.60), we get
Let Ω
t
denote the information generated by ε
t
, ε
t − 1, …, ε1
. Choosing an arbitrary initial value to ![]() , we obtain
, we obtain ![]() and
and
for
i ≥ 2. It follows that ![]() . Note however that the conditional distribution of
r
t + 1 + ⋯ + r
t + h
is not exactly
. Note however that the conditional distribution of
r
t + 1 + ⋯ + r
t + h
is not exactly ![]() (Exercise 11.19). Many practitioners, however, systematically use the erroneous formula
(Exercise 11.19). Many practitioners, however, systematically use the erroneous formula
GARCH‐Based Estimation
Of course, one can use more sophisticated GARCH‐type models, rather than the degenerate version of RiskMetrics. To estimate VaR
t
(1, α), it suffices to use Relation ( 11.60) and to estimate
q
t
(1, α) by ![]() , where
, where ![]() is the conditional variance estimated by a GARCH‐type model (for instance, an EGARCH or TGARCH to account for the leverage effect; see Chapter 4), and
is the conditional variance estimated by a GARCH‐type model (for instance, an EGARCH or TGARCH to account for the leverage effect; see Chapter 4), and ![]() is an estimate of the distribution of the normalised residuals. It is, however, important to note that, even for a simple Gaussian GARCH(1, 1), there is no explicit available formula for computing
q
t
(h, α) when
h > 1. Apart from the case
h = 1, simulations are required to evaluate this quantile (but, as can be seen from Exercise 11.19, this should also be the case with the RiskMetrics method). The following procedure may then be suggested:
is an estimate of the distribution of the normalised residuals. It is, however, important to note that, even for a simple Gaussian GARCH(1, 1), there is no explicit available formula for computing
q
t
(h, α) when
h > 1. Apart from the case
h = 1, simulations are required to evaluate this quantile (but, as can be seen from Exercise 11.19, this should also be the case with the RiskMetrics method). The following procedure may then be suggested:
- Fit a model, for instance a GARCH(1, 1), on the observed returns
r
t
= ε
t
,
t = 1, …, n
, and deduce the estimated volatility
 for
t = 1, …, n + 1.
for
t = 1, …, n + 1. - Simulate a large number
N
of scenarios for ε
n + 1, …, ε
n + h
by iterating, independently for
i = 1, …, N
, the following three steps:
- (b1) simulate the values
 iid with the distribution
iid with the distribution  ;
; - (b2) set
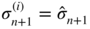 and
and  ;
; - (b3) for
k = 2, …, h
, set
 and
and 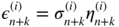 .
.
- (b1) simulate the values
- Determine the empirical quantile of simulations
 ,
i = 1, …, N
.
,
i = 1, …, N
.
The distribution ![]() can be obtained parametrically or non‐parametrically. A simple non‐parametric method involves taking for
can be obtained parametrically or non‐parametrically. A simple non‐parametric method involves taking for ![]() the empirical distribution of the standardised residuals
the empirical distribution of the standardised residuals ![]() , which amounts to taking, in step (b1), a bootstrap sample of the standardised residuals.
, which amounts to taking, in step (b1), a bootstrap sample of the standardised residuals.
Assessment of the Estimated VaR (Backtesting)
The Basel accords allow financial institutions to develop their own internal procedures to evaluate their techniques for risk measurement. The term ‘backtesting’ refers to procedures comparing, on a test (out‐of‐sample) period, the observed violations of the VaR (or any other risk measure), the latter being computed from a model estimated on an earlier period (in‐sample).
To fix ideas, define the variables corresponding to the violations of VaR (‘hit variables’)
Ideally, we should have

that is, a correct proportion of effective losses which violate the estimated VaRs, with a minimal average cost.
Numerical Illustration
Consider a portfolio constituted solely by the CAC 40 index, over the period from 1 March 1990 to 23 April 2007. We use the first 2202 daily returns, corresponding to the period from 2 March 1990 to 30 December 1998, to estimate the volatility using different methods. To fix ideas, suppose that on 30 December 1998, the value of the portfolio was, in French Francs, the equivalent of €1 million. For the second period, from 4 January 1999 to 23 April 2007 (2120 values), we estimated VaR at horizon h = 1 and level α = 1% using four methods.
The first method (historical) is based on the empirical quantiles of the last 250 returns. The second method is RiskMetrics. The initial value for ![]() was chosen equal to the average of the squared last 250 returns of the period from 2 March 1990 to 30 December 1998, and we took
λ = 0.94. The third method (GARCH‐
was chosen equal to the average of the squared last 250 returns of the period from 2 March 1990 to 30 December 1998, and we took
λ = 0.94. The third method (GARCH‐![]() ) relies on a GARCH(1, 1) model with Gaussian
) relies on a GARCH(1, 1) model with Gaussian ![]() innovations. With this method we set
innovations. With this method we set ![]() , the 1% quantile of the
, the 1% quantile of the ![]() distribution. The last method (GARCH‐NP) estimates volatility using a GARCH(1, 1) model, and approximates
distribution. The last method (GARCH‐NP) estimates volatility using a GARCH(1, 1) model, and approximates ![]() by the empirical 1% quantile of the standardised residuals. For the last two methods, we estimated a GARCH(1, 1) on the first period, and kept this GARCH model for all VaR estimations of the second period. The estimated VaR and the effective losses were compared for the 2120 data of the second period.
by the empirical 1% quantile of the standardised residuals. For the last two methods, we estimated a GARCH(1, 1) on the first period, and kept this GARCH model for all VaR estimations of the second period. The estimated VaR and the effective losses were compared for the 2120 data of the second period.
Table 11.1 and Figure 11.2 do not allow us to draw definitive conclusions, but the historical method appears to be outperformed by the NP‐GARCH method. On this example, the only method which adequately controls the level 1% is the NP‐GARCH, which is not surprising since the empirical distribution of the standardised residuals is very far from Gaussian.
Table 11.1 Comparison of the four VaR estimation methods for the CAC 40.
| Historic | Risk metrics |
GARCH‐ |
GARCH‐NP | |
| Average estimated VaR (€) | 38 323 | 32 235 | 31 950 | 35 059 |
| Number of losses > VaR | 29 | 37 | 37 | 21 |
On the 2120 values, the VaR at the 1% level should only be violated 2120 × 1% = 21.2 times on average.

Figure 11.2
Effective losses of the CAC 40 (solid lines) and estimated VaRs (dotted lines) in thousands of euros for the historical method (a), RiskMetrics (b), GARCH‐ (c), and GARCH‐NP (d).
(c), and GARCH‐NP (d).
11.4 Bibliographical Notes
A detailed presentation of the financial concepts introduced in this chapter is provided in the books by Gouriéroux and Jasiak (2001) and Franke, Härdle, and Hafner (2004). A classical reference on the stochastic calculus is the book by Karatzas and Shreve (1988).
The relation between continuous‐time processes and GARCH processes was established by Nelson (1990b) (see also Nelson 1992; Nelson and Foster 1994, 1995). The results obtained by Nelson rely on concepts presented in the monograph by Stroock and Varadhan (1979). A synthesis of these results is presented in Elie (1994). An application of these techniques to the TARCH model with contemporaneous asymmetry is developed in El Babsiri and Zakoïan (1990).
When applied to high‐frequency (intraday) data, diffusion processes obtained as GARCH limits when the time unit tends to zero are often found inadequate, in particular because they do not allow for daily periodicity. There is a vast literature on the so‐called realised volatility, which is a daily measure of daily return variability. See Barndorff‐Nielsen and Shephard (2002), Andersen et al. (2003) and Andersen et al. (2011) for econometric approaches to realised volatility. In Andersen et al. (2003), it is argued that ‘standard volatility models used for forecasting at the daily level cannot readily accommodate the information in intraday data, and models specified directly for the intraday data generally fail to capture the longer interdaily volatility movements sufficiently well’. Another point of view is defended in the thesis by Visser (2009) in which it is shown that intraday price movements can be incorporated into daily GARCH models.
Concerning the pricing of derivatives, we have purposely limited our presentation to the elementary definitions. Specialised monographs on this topic are those of Dana and Jeanblanc‐Picqué (1994) and Duffie (1994). Many continuous‐time models have been proposed to extend the Black and Scholes (1973) formula to the case of a non‐constant volatility. The Hull and White (1987) approach introduces a SDE for the volatility but is not compatible with the assumption of a complete market. To overcome this difficulty, Hobson and Rogers (1998) developed a stochastic volatility model in which no additional Brownian motion is introduced. A discrete‐time version of this model was proposed and studied by Jeantheau (2004).
The characterisation of the risk‐neutral measure in the GARCH case is due to Duan (1995). Numerical methods for computing option prices were developed by Engle and Mustafa (1992) and Heston and Nandi (2000), among many others. Problems of option hedging with pricing models based on GARCH or stochastic volatility are discussed in Garcia, Ghysels, and Renault (1998). The empirical performance of pricing models in the GARCH framework is studied by Härdle and Hafner (2000), Christoffersen and Jacobs (2004) and the references therein. Valuation of American options in the GARCH framework is studied in Duan and Simonato (2001) and Stentoft (2005). The use of the realised volatility, based on high‐frequency data is considered in Stentoft (2008). Statistical properties of the realised volatility in stochastic volatility models are studied by Barndorff‐Nielsen and Shephard (2002).
Introduced by Engle, Lilien, and Robins (1987), ARCH‐M models are characterised by a linear relationship between the conditional mean and variance of the returns. These models were used to test the validity of the intertemporal capital asset pricing model of Merton (1973) which postulates such a relationship (see, for instance, Lanne and Saikkonen 2006). The asymptotic properties of the quasi‐maximum likelihood estimator (QMLE) of GARCH‐in‐Mean models have been studied by Conrad and Mammen (2016).
The concept of the SDF was developed by Hansen and Richard (1987) and, more recently, by Cochrane (2001). Our presentation follows that of Gouriéroux and Tiomo (2007). This method is used in Bertholon, Monfort, and Pegoraro (2008).
The concept of coherent risk measures (Definition 11.2) was introduced by Artzner et al. (1999), initially on a finite probability space, and extended by Delbaen (2002). In the latter article it is shown that, for the existence of coherent risk measures, the set ℒ cannot be too large, for instance the set of all absolutely continuous random variables. Alternative axioms were introduced by Wang, Young, and Panjer (1997), initially for risk analysis in insurance. Dynamic VaR models were proposed by Koenker and Xiao (2006) (quantile autoregressive models), Engle and Manganelli (2004) (conditional autoregressive VaR), Gouriéroux and Jasiak (2008) (dynamic additive quantile). The issue of assessing risk measures was considered by Christoffersen (1998), Christoffersen and Pelletier (2004), Engle and Manganelli (2004) and Hurlin and Tokpavi (2006), among others. The article by Escanciano and Olmo (2010) considers the impact of parameter estimation in risk measure assessment. Evaluation of VaR at horizons longer than 1, under GARCH dynamics, is discussed by Ardia (2008).
11.5 Exercises
11.1 (Linear SDE)
Consider the linear SDE ( 11.6). Letting ![]() denote the solution obtained for
ω = 0, what is the equation satisfied by
denote the solution obtained for
ω = 0, what is the equation satisfied by ![]() ?
?
Hint: the following result, which is a consequence of the multidimensional Itô formula, can be used. If ![]() is a two‐dimensional process such that, for a real Brownian motion (W
t
),
is a two‐dimensional process such that, for a real Brownian motion (W
t
),

under standard assumptions, then
Deduce the solution of Eq. ( 11.6) and verify that if ω ≥ 0, x 0 ≥ 0 and (ω, x 0) ≠ (0, 0), then this solution will remain strictly positive.
- 11.2 (Convergence of the Euler discretisation) Show that the Euler discretisation ( 11.15), with μ and σ continuous, converges in distribution to the solution of the SDE ( 11.1), assuming that this equation admits a unique (in distribution) solution.
-
11.3 (Another limiting process for the GARCH(1, 1) (Corradi 2000)) Instead of the rates of convergence of Example 11.2 for the parameters of a GARCH(1, 1), consider

Give an example of the sequence (ω τ , α τ , β τ ) compatible with these conditions. Determine the limiting process of
 when
τ → 0. Show that, in this model, the volatility
when
τ → 0. Show that, in this model, the volatility  has a non‐stochastic limit when
t → ∞ .
has a non‐stochastic limit when
t → ∞ .
- 11.4 (Put–call parity) Using the martingale property for the actualised price under the risk‐neutral probability, deduce the European put option price from the European call option price.
- 11.5 (Delta of a European call) Compute the derivative with respect to S t of the European call option price and check that it is positive.
-
11.6 (Volatility of an option price) Show that the European call option price
C
t
= C(S, t) is solution of an SDE of the form

with

- 11.7 (Estimation of the drift and volatility) Compute the maximum likelihood estimators of μ and σ 2 based on observations S 1, …, S n of the geometric Brownian motion.
- 11.8 (Vega of a European call) A measure of the sensitivity of an option to the volatility of the underlying asset is the so‐called vega coefficient defined by ∂C t /∂σ . Compute this coefficient for a European call and verify that it is positive. Is this intuitive?
- 11.9 (Martingale property under the risk‐neutral probability) Verify that under the measure π defined in Model ( 11.52), the actualised price e −rt S t is a martingale.
-
11.10 (Risk‐neutral probability for a non‐linear GARCH model) Duan (1995) considered the model

where ω > 0, α, β ≥ 0, and
 . Establish the strict and second‐order stationarity conditions for the process (ε
t
). Determine the risk‐neutral probability using SDFs, chosen to be affine exponential with time‐dependent coefficients.
. Establish the strict and second‐order stationarity conditions for the process (ε
t
). Determine the risk‐neutral probability using SDFs, chosen to be affine exponential with time‐dependent coefficients. -
11.11 (A non‐affine exponential SDF) Consider an SDF of the form

Show that, by an appropriate choice of the coefficients a t , b t , and c t , with c t ≠ 0, a risk‐neutral probability can be obtained for model ( 11.51). Derive the risk‐neutral version of the model and verify that the volatility differs from that of the initial model.
- 11.12 (An erroneous computation of the VaR at horizon h) The aim of this exercise is to show that Relation (11.57) may be wrong if the price variations are iid but non‐Gaussian. Suppose that (a ′ΔP t ) is iid, with a double exponential density with parameter λ , given by f(x) = 0.5λ exp {−λ ∣ x∣}. Calculate VaR t, 1(α). What is the density of L t, t + 2 ? Deduce the equation for VaR at horizon 2. Show, for instance for λ = 0.1, that VaR is overevaluated if Relation ( 11.57) is applied with α = 0.01, but is underevaluated with α = 0.05.
- 11.13 (VaR for AR(1) prices variations) Check that formula ( 11.58) is satisfied.
- 11.14 (VaR for ARCH(1) prices variations) Suppose that the price variations follow an ARCH(1) model (11.59). Show that the distribution of ΔP t + 2 conditional on the information at time t is not Gaussian if α 1 > 0. Deduce that VaR at horizon 2 is not easily computable.
- 11.15 (VaR and conditional quantile) Derive formula ( 11.60), giving the relationship between VaR and the returns conditional quantile.
- 11.16 (Integral formula for the ES) Using the fact that L t, t + h and F −1(U) have the same distribution, where U denotes a variable uniformly distributed on [0,1] and F the cdf of L t, t + h , derive formula ( 11.64).
-
11.17 (Coherence of the ES) Prove that the ES is a coherent risk measure.
Hint for proving subadditivity: For L i such that
 ,
i = 1, 2, 3, denote the VaR at level
α
by VaR
i
(α) and the ES by
,
i = 1, 2, 3, denote the VaR at level
α
by VaR
i
(α) and the ES by  . For
L
3 = L
1 + L
2
, compute
α{ES1(α) + ES2(α) − ES3(α)} using expectations and observe that
. For
L
3 = L
1 + L
2
, compute
α{ES1(α) + ES2(α) − ES3(α)} using expectations and observe that
-
11.18 (RiskMetrics is a prediction method, not really a model) For any initial value
 let (ε
t
)
t ≥ 1
be a sequence of random variables satisfying the Risk Metrics model ( 11.66) for any
t ≥ 1. Show that ε
t
→ 0 almost surely as
t → ∞.
let (ε
t
)
t ≥ 1
be a sequence of random variables satisfying the Risk Metrics model ( 11.66) for any
t ≥ 1. Show that ε
t
→ 0 almost surely as
t → ∞. - 11.19 (At horizon h > 1 the conditional distribution of the future returns is not Gaussian with RiskMetrics) Prove that in the RiskMetrics model, the conditional distribution of the returns at horizon 2, r t + 1 + r t + 2 , is not Gaussian. Conclude that formula (11.67) is incorrect.
