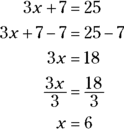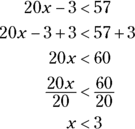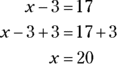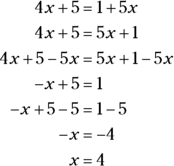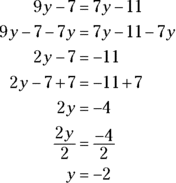Chapter 9
Knowing Your Math
IN THIS CHAPTER
![]() Understanding math-talk and basic concepts
Understanding math-talk and basic concepts
![]() Finagling fractions and decimals
Finagling fractions and decimals
![]() Brushing up on positive and negative numbers
Brushing up on positive and negative numbers
![]() Getting into roots, exponents, and quadratics
Getting into roots, exponents, and quadratics
![]() Digging into algebra and geometry
Digging into algebra and geometry
Lazarus Long, a fictional character created by Robert A. Heinlein, once said, “Anyone who cannot cope with mathematics isn’t fully human. At best, he is a tolerable subhuman who has learned to wear shoes, bathe, and not make messes in the house.”
Perhaps Mr. Long’s observation is a little harsh. Some people seem to be born mathematicians, while others struggle with many of its concepts. The fact remains, however, that the military seems to agree with Mr. Long. You can’t join the military without proving that you know the fundamentals of math. Fully 50 percent of your AFQT score is based on your ability to solve math problems. And as I indicate in Chapter 2, your AFQT score determines whether you can join the military.
The good news is that although the military wants you well-grounded in math, it’s not looking for rocket scientists. That’s NASA’s job. The two math subtests of the AFQT test your math ability only at the high school level, so you don’t have to break out any advanced calculus or plot the orbit of subatomic particles.
While I was deciding what to cover in this chapter, I quickly realized that I can’t give you an entire high school math education in one chapter. Heck, I couldn’t do that in one whole book. Then I realized that I don’t have to try to cram all the math you learned in 13 years of school into one chapter. If you’re reading this book, you’re obviously interested in joining the military. And to join the military, you must be either a high school graduate or have a high school equivalency certificate, or you must have at least 15 college credits. That means you’ve already learned this stuff. All I need to do is provide you a bit of a refresher to remind you of all those math rules you may have forgotten or stashed away in the back of your mind. And that’s what you find here: a refresher course, designed to draw out all the math you should already know!
So look at it this way: You already know what you need to know in order to ace the AFQT. Your job is just to remind yourself of what you know. In this chapter, I help you do exactly that.
Making the Most of Math Terminology
Some people are intimidated by math in part because it has its own language. In Chapter 11, I explain how to use keywords in math word problems to translate English into mathematical equations. But that’s not enough. You need to know basic math terminology to solve many of the problems you see on the two math subtests that make up the AFQT.
I just looked in my handy-dandy pocket math dictionary. There are more than 700 mathematical terms listed there. Wait a minute! Sit back down. You don’t need to memorize 700 terms. You won’t see the math term brachistochrone on any of the subtests, for example.
Although you don’t need to know 700 math terms, you should memorize the most common terms because you’re likely to see them used in one way or another on the Mathematics Knowledge subtest or the Arithmetic Reasoning subtest. Here’s some of what you need to know:
- Average: The average usually refers to the arithmetic mean or just the mean average. To find the mean of a set of n numbers, add the numbers in the set and divide the sum by n. For example, the average (or arithmetic mean) of 3, 7, 10, and 12 is
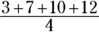 , or 8.
, or 8. - Coefficient: The coefficient is a number multiplied by a variable or by a product of variables or by powers of variables in a term. For example, 123 is the coefficient in the term
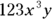 .
. - Evaluate: Evaluate means to figure out or calculate. If you’re asked to evaluate
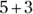 , that means to simplify the expression to 8.
, that means to simplify the expression to 8. - Integer: An integer is a whole number that can be expressed without a decimal or fraction component. Examples of integers include 1, 70, and –583.
- Pi: In math equations and terms, pi is usually expressed by its Greek letter,
 . Pi represents the ratio of the circumference of a circle to its diameter, and it’s used in several formulas, especially formulas involving geometry. Pi’s value is 3.141592653589793… (on and on forever), but using the value 3.14 or
. Pi represents the ratio of the circumference of a circle to its diameter, and it’s used in several formulas, especially formulas involving geometry. Pi’s value is 3.141592653589793… (on and on forever), but using the value 3.14 or 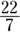 is traditional in common math problems.
is traditional in common math problems. -
Prime/composite numbers: A prime number is a positive integer that can be divided evenly only by itself and 1. For example, 2, 3, 5, 7, 11, 13 are the first six primes. One afternoon, all the famous mathematicians got together over a beer and agreed among themselves that 1 isn’t a prime number.
Positive numbers that have factors other than themselves and 1 as factors are called composite numbers. Again, by convention, 1 isn’t considered a composite number.
- Product: The product is the result of multiplication. The product of 2 and 9 is 18.
-
Quotient/remainder: The quotient is the result of division. 40 divided by 5 has a quotient of 8.
But what if one number doesn’t divide evenly into the other? The remainder is what’s left over in that scenario. 43 divided by 5 has a quotient of 8 and a remainder of 3.
- Reciprocal: A reciprocal is a fraction flipped upside down. The reciprocal of x is
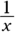 . The reciprocal of
. The reciprocal of 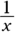 is x, and
is x, and  .
. - Sum: The sum is the result of addition. The sum of 3 and 6 is 9.
You’re not done with math vocabulary yet. You still need to know many more math words and terms. I explain them throughout the rest of the chapter.
The Heart of Math: Exploring Expressions and Equations
Math without expressions and equations is like a fire hydrant without a dog; they just go together. So what’s the difference between a mathematical expression and an equation?
- An expression is any mathematical calculation or formula combining numbers and/or variables. Expressions don’t include equal signs (=). For example,
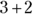 is an expression, and so is
is an expression, and so is 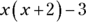 .
. - An equation, on the other hand, is a mathematical sentence built from expressions connected by an equal sign (=). For example,
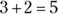 is an equation, and
is an equation, and  is also an equation.
is also an equation.
This section gives you the lowdown on keeping equations balanced and simplifying expressions.
Keeping equations balanced
One of the coolest things about equations is that you can do almost anything you want to them as long as you remember to do the exact same thing to both sides of the equation. This rule is called keeping the equation balanced. For example, if you have the equation ![]() , you can add 3 to both sides of the equation, and it still balances out:
, you can add 3 to both sides of the equation, and it still balances out: ![]() . You can divide both sides by 3, and it still balances:
. You can divide both sides by 3, and it still balances: ![]() .
.
Obeying the order of operations
In math, you must solve equations by following steps in a proper order. If you don’t, you won’t get the right answer. Many of the most frequent math errors occur when people don’t follow the order of operations when solving mathematical problems.
-
Start with any calculations in brackets or parentheses.
When you have nested parentheses or brackets (parentheses or brackets inside other parentheses or brackets), do the inner ones first and work your way outward.
Groupings where parentheses are implied, such as numerators or denominators (like
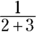 ) or the numbers under a radical (like
) or the numbers under a radical (like 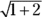 ), are performed first, just as they would be if there were official parentheses around them.
), are performed first, just as they would be if there were official parentheses around them. - Do any terms with exponents and roots.
- Complete any multiplication and division, in order from left to right.
- Do any addition and subtraction, in order from left to right.
Take the following expression out for a ride.
 Solve:
Solve: ![]() .
.
Do the calculations in the parentheses first:
Next, simplify the exponents:
Do multiplication and division from left to right:
Finally, perform addition and subtraction from left to right:
Mental math: Mixing it up with the commutative, associative, and distributive properties
The commutative and associative properties: Moving numbers in your head
The commutative and associative properties let you break the rules about adding or multiplying from left to right. The commutative property of addition says you can rearrange the numbers you’re adding without changing the result:

Similarly, the associative property of addition lets you decide how to group the numbers you’re adding:
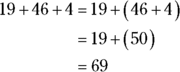
Together, these properties let you add a string of numbers in whatever order you like. For example, you can make calculations easier by pairing up numbers whose ones digits add up to 10 before adding other numbers in the list.
Because subtracting is essentially the same thing as adding a negative number, you can extend these addition properties to subtraction problems, too — just be careful to keep track of the negative signs (see the later section “Playing with Positive and Negative Numbers” for details). The following example shows how smart groupings can let you add and subtract figures faster. Notice which calculations are easier to do in your head.
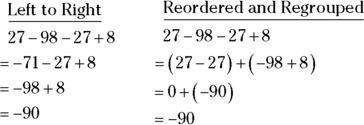
Similarly, the commutative and associative properties of multiplication let you multiply numbers in any order you like. Check out how switching the numbers around can make mental math easier:

You can even use these multiplication properties with division, as long as you remember that division is the same thing as multiplying by a fraction (see the later section “Multiplying fractions”):
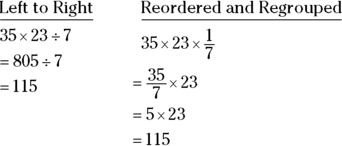
The distributive property: Breaking up large numbers
Have you ever envied those people who can perform calculations on large numbers in their heads? What if I told you that you can be one of those people? That’s right. All you have to do is practice the distributive property of math.
The distributive property, often referred to as the distributive law of math, lets you separate or break larger numbers into parts for simpler arithmetic. It basically says that ![]() is the same as
is the same as ![]() .
.
Suppose you want to mentally multiply 4 by 53; ![]() is the same as
is the same as ![]() . Four times 50 is easy; it’s 200. Four times 3 is also easy. It’s 12. Two hundred plus 12 is 212.
. Four times 50 is easy; it’s 200. Four times 3 is also easy. It’s 12. Two hundred plus 12 is 212.
Try another one with a bit of a twist.
 Mentally perform the calculation
Mentally perform the calculation ![]() .
.
![]() is equivalent to
is equivalent to ![]() .
.
You can quickly mentally calculate that 12 times 20 is 240 and that 12 times 1 is 12. Subtract 12 from 240, and you have 228.
Figure 9-1 illustrates how this process works.
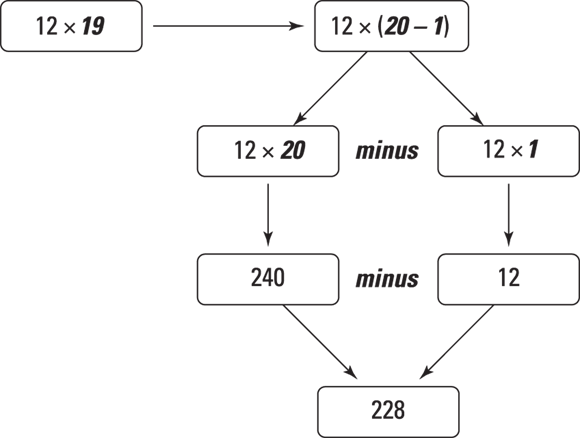
© John Wiley & Sons, Inc.
FIGURE 9-1: Using mental math to multiply large numbers.
If ![]() is still too large for mental calculation, you can break it down as
is still too large for mental calculation, you can break it down as ![]() , or
, or ![]() .
.
You can also use the distributive property for division, although that takes a bit more practice: ![]() is the same as
is the same as ![]() . You can quickly calculate that 340 divided by 2 is 170, and 170 divided by 2 is 85.
. You can quickly calculate that 340 divided by 2 is 170, and 170 divided by 2 is 85.
Or you can express ![]() as
as ![]() . You can mentally calculate 100 divided by 4 as 25. Forty divided by 4 is also easy — it’s 10. So
. You can mentally calculate 100 divided by 4 as 25. Forty divided by 4 is also easy — it’s 10. So ![]() . Keep practicing, and you’ll be known as the neighborhood lightning calculator.
. Keep practicing, and you’ll be known as the neighborhood lightning calculator.
Having Fun with Factors
A factor is simply a number that is multiplied to get a product. Factoring a number means taking the number apart. It’s kind of like multiplying in reverse. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because all these numbers can be divided evenly into 12.
Here are some other factors:
- 2: 1, 2
- 3: 1, 3
- 4: 1, 2, 4
- 5: 1, 5
- 6: 1, 2, 3, 6
- 16: 1, 2, 4, 8, 16
- 20: 1, 2, 4, 5, 10, 20
- 45: 1, 3, 5, 9, 15, 45
Understanding types of factors
A factor can be either a prime number or a composite number (except 1 and 0 are neither prime nor composite). As I mention in the section “Making the Most of Math Terminology” earlier in this chapter, prime numbers have only themselves and 1 as factors, while composite numbers can be divided evenly by other numbers.
Finding prime factors
Any composite number can be written as a product of prime factors. Mathematicians call this process prime factorization. To find the prime factors of a number, you divide the number by the smallest possible prime number and work up the list of prime numbers until the result is itself a prime number.
Say you want to find the prime factors of 240. Because 240 is even, start by dividing it by the smallest prime number, which is 2: ![]() . The number 120 is also even, so it can be divided by 2:
. The number 120 is also even, so it can be divided by 2: ![]() . Then
. Then ![]() and
and ![]() . Now, 15 isn’t even, so check to see whether you can divide it by 3 (the next highest prime number);
. Now, 15 isn’t even, so check to see whether you can divide it by 3 (the next highest prime number); ![]() , which itself is a prime number, so 240 is now fully factored.
, which itself is a prime number, so 240 is now fully factored.
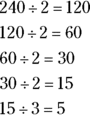
Now, simply list what you divided by to write the prime factors of 240. The prime factors of 240 are ![]() .
.
Looking at Least Common Multiples
A common multiple is a number that is a multiple of two or more numbers. For example, 20, 30, and 40 are common multiples of the numbers 5 and 10. The least common multiple (LCM) of two or more numbers is the smallest number (not zero) that’s a multiple of both or all the numbers. The LCM is useful in solving many math problems — especially those involving fractions (check out the following section for info on working with fractions).
One way to find the LCM is to list the multiples of each number, one at a time, until you find the smallest multiple that’s common to all the numbers.
 Find the LCM of 45 and 50.
Find the LCM of 45 and 50.
- Multiples of 45: 45, 90, 135, 180, 225, 270, 315, 360, 405, 450
- Multiples of 50: 50, 100, 150, 200, 250, 300, 350, 400, 450
The LCM of 45 and 50 is 450.
- The prime factors for 45 are
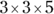 .
. - The prime factors for 50 are
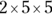 .
.
Then multiply each factor the greatest number of times it occurs in either number. If the same factor occurs more than once in both numbers, you multiply the factor the greatest number of times it occurs. For example, 5 occurs as a prime factor of both 45 (where it occurs once) and 50 (where it occurs twice); the two occurrences in the factorization of 50 beat the single occurrence in the factorization of 45. The number 3 occurs two times, 5 occurs two times, and 2 occurs once, so you have ![]() .
.
Now that you’re getting the hang of it, try another one:
 What is the least common multiple of 5, 27, and 30?
What is the least common multiple of 5, 27, and 30?
List the prime factors of each number:
- Prime factors of 5: 5
- Prime factors of 27:
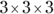
- Prime factors of 30:
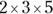
The number 3 occurs a maximum of three times, 5 occurs a maximum of one time, and 2 occurs a maximum of one time: ![]() . Check your answer by seeing whether 5, 27, and 30 can all divide evenly into 270.
. Check your answer by seeing whether 5, 27, and 30 can all divide evenly into 270.
Conquering the Fear of Fractions
I don’t know why, but most people I’ve talked to don’t like to do math with fractions. Maybe it’s because teachers always used pies as examples, and that just makes people hungry. The pies were all imaginary, too, so you didn’t even get a piece after all the figuring was done. I’m going to break convention and use squares of cardboard instead. Sure, they’re harder to cut than pies, but they don’t smell as enticing.
A fraction is nothing more than part of a whole. Take a look at Figure 9-2.
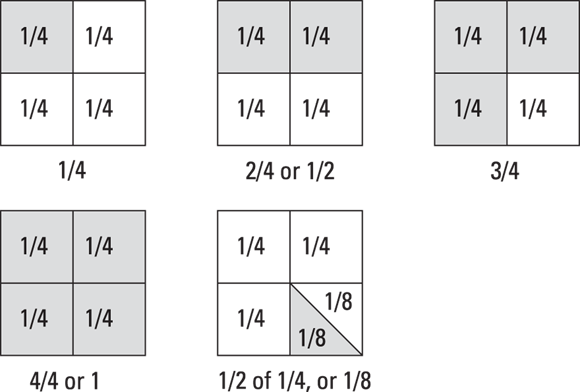
© John Wiley & Sons, Inc.
FIGURE 9-2: Fractions are part of a whole.
Each shaded area represents part of a whole, or a fraction of the whole. It doesn’t have to be fourths. If I had divided the cardboard into two equal pieces, each shaded area would represent one-half. If the cardboard were cut into three equal pieces, each piece would be one-third of the whole.
Fractions aren’t difficult to work into your mathematical skills as long as you remember a few rules and techniques.
Defining parts and types of fractions
The top number of a fraction is called the numerator. The bottom number is known as the denominator. For example, in the fraction ![]() , 7 is the numerator and 16 is the denominator.
, 7 is the numerator and 16 is the denominator.
If the numerator is smaller than the denominator, the fraction is less than a whole (smaller than 1). This kind of fraction is called a proper fraction. The fraction ![]() is a proper fraction, as is
is a proper fraction, as is ![]() .
.
If the numerator is larger than the denominator, the fraction is larger than a whole (larger than 1), and the fraction is called an improper fraction. The fraction ![]() is an improper fraction.
is an improper fraction.
Simplifying fractions
Simplifying (or reducing) fractions means to make the fraction as simple as possible. You’re usually required to simplify fractions on the ASVAB math subtests before you can select the correct answer. For example, if you worked out a problem and the answer was ![]() , the correct answer choice on the math subtest would probably be
, the correct answer choice on the math subtest would probably be ![]() , which is the simplest equivalent to
, which is the simplest equivalent to ![]() .
.
Many methods of simplifying fractions are available. In this section, I give you the two that I think are the easiest; you can decide which is best for you.
Method 1: Dividing by the lowest prime numbers
Try dividing the numerator and denominator by the lowest prime numbers until you can’t go any further. (The earlier section “Understanding types of factors” has details on this process.)
 Simplify
Simplify ![]() .
.
Both the numerator and denominator are even numbers, so they can be divided by the lowest prime number, which is 2. Then ![]() , and
, and ![]() . The result is
. The result is ![]() .
.
The numerator and denominator are both still even numbers, so divide by 2 again: ![]() , and
, and ![]() . The result is
. The result is ![]() .
.
This time the denominator is an odd number, so you know it isn’t divisible by 2. Try the next highest prime number, which is 3: ![]() , and
, and ![]() . The result is
. The result is ![]() .
.
Because no common prime numbers divide evenly into both 2 and 9, the fraction is fully simplified.
Method 2: Listing prime factors
This method of simplification is my favorite. Simply list the prime factors of both the numerator and the denominator as explained in the earlier section “Finding prime factors” and then see whether any cancel out (are the same).
 Simplify
Simplify ![]() .
.
The prime factors of 24 are ![]() .
.
The prime factors of 108 are ![]() .
.
You can now write the fraction as ![]() .
.
Two of the 2s and one of the 3s cancel out, so you can remove them from both the numerator and the denominator. What’s left is ![]() , or
, or ![]() .
.
Multiplying fractions
Multiplying fractions is very easy. All you have to do is multiply the numerators by each other, multiply the denominators by each other, and then simplify the result, as shown in the following equation:
The fraction ![]() can be simplified to
can be simplified to ![]() (see the earlier section “Simplifying fractions”).
(see the earlier section “Simplifying fractions”).
If you can cross-cancel before you multiply, multiplying fractions is even easier. Here’s the same problem. The 3 in the numerator and the 15 in the denominator have a common factor: They’re both divisible by 3. If you divide both by 3 before multiplying, you don’t have to reduce the fraction at the end:
The end result is ![]() .
.
Dividing fractions
Dividing fractions is almost the same as multiplying, with one important difference: You have to convert the second fraction (the divisor) to the reciprocal and then multiply. As I explain in the earlier “Making the Most of Math Terminology” section, the reciprocal is simply a fraction flipped over.
 Solve:
Solve: ![]() .
.
Take the reciprocal of the second fraction and multiply it by the other fraction:
The fraction ![]() is an improper fraction, which you can convert to
is an improper fraction, which you can convert to ![]() (see the earlier section “Defining parts and types of fractions”). Then you can simplify
(see the earlier section “Defining parts and types of fractions”). Then you can simplify ![]() to
to ![]() (see the earlier section “Simplifying fractions”).
(see the earlier section “Simplifying fractions”).
Adding and subtracting fractions
Adding and subtracting fractions can be as simple as multiplying and dividing them, or it can be more difficult. As the following sections show, it all depends on whether the fractions have the same denominator.
Adding and subtracting fractions with like denominators
To add or subtract two fractions with the same denominator, add (or subtract) the numerators and place that sum (or difference) over the common denominator:
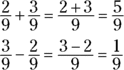
Adding and subtracting fractions with different denominators
You can’t add or subtract fractions with different denominators. You have to convert the fractions so they all have the same denominator, and then you perform addition or subtraction as I explain in the preceding section.
Converting fractions so they share the same denominator involves finding a common denominator. A common denominator is nothing more than a common multiple of all the denominators, as I describe in the earlier section “Looking at Least Common Multiples.”
 Find a common denominator for the fractions
Find a common denominator for the fractions ![]() and
and ![]() .
.
The multiples of 5 are 5, 10, 15, 20, 25, 30, 35, and 40.
The multiples of 8 are 8, 16, 24, 32, and 40.
A common denominator for the fractions ![]() and
and ![]() is 40.
is 40.
The next step in the addition/subtraction process is to convert the fractions so they share the common denominator. To do this, divide the original denominator into the new common denominator and then multiply the result by the original numerator.
Start with ![]() . Divide the original denominator (5) into the new common denominator (40):
. Divide the original denominator (5) into the new common denominator (40): ![]() . Next, multiply the result (8) by the original numerator (3):
. Next, multiply the result (8) by the original numerator (3): ![]() . The equivalent fraction is
. The equivalent fraction is ![]() .
.
Perform the same operation with the second fraction, ![]() . Divide the original denominator (8) into the new common denominator (40):
. Divide the original denominator (8) into the new common denominator (40): ![]() . Next, multiply this (5) by the original numerator (1):
. Next, multiply this (5) by the original numerator (1): ![]() . The equivalent fraction is
. The equivalent fraction is ![]() .
.
Now that the fractions have the same denominator, you can add or subtract them as shown in the preceding section:
Performing multiple operations
Sometimes you have to work through more than one operation on a set of fractions. Give this one a try:

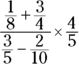
On the surface, this problem looks complicated. But if you remember the order of operations (see the earlier section “Obeying the order of operations”) and take the problem one step at a time, it’s really easy.
Under the order of operations, you do the work in the implied sets of parentheses (the top and bottom of the big fraction) first:
If you write the big fraction bar as a division sign, the problem now reads ![]() .
.
Continue by performing the next operation in the parentheses:
The problem is now much simpler: ![]() .
.
Converting fractions to decimals
Some math problems require you to perform operations on both decimal numbers (see the later section “Dealing with Decimals”) and fractions. To properly perform such calculations, you must either convert the fraction to a decimal number or convert the decimal to a fraction.
Converting a fraction to a decimal number is easy. You simply divide the numerator by the denominator. For example ![]() is
is
Try the following:
 Solve:
Solve: ![]() .
.
Convert the fraction to a decimal by dividing the numerator by the denominator:
Now you can easily perform the operation: ![]() .
.
Comparing fractions
The two math subtests of the ASVAB often ask you to compare fractions to determine which one is the largest or smallest. If the fractions all have the same denominator, it’s easy. The fraction with the largest numerator is the largest, and the one with the smallest numerator is the smallest.
But how do you compare fractions that have different denominators? I’ll leave it up to you to determine which of the following proven methods you like the best.
Method 1: Finding a common denominator
The first method is to convert the fractions so they all have a common denominator (see the earlier section “Adding and subtracting fractions with different denominators”). After conversion, the fraction with the largest numerator is the largest fraction, and the one with the smallest numerator is the smallest. This method is what you probably learned in school.
 Which of the following fractions is the largest:
Which of the following fractions is the largest: ![]() ,
, ![]() ,
, ![]() , or
, or ![]() ?
?
First, find a common multiple for the denominators:
- The multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156, 168, 180, 192, 204, 216, 228, 240.
- The multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 100, 104, 108, 112, 116, 122, … , 240.
- The multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240.
- The multiples of 16: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240.
The lowest common denominator for all four fractions is 240.
Next, convert all the fractions so they have a denominator of 240 by dividing the new common denominator by the original denominator of the fraction and then multiplying the result by the original numerator:
The largest fraction is the one with the largest numerator: ![]() , or
, or ![]() .
.
Method 2: The cross-product method
You may find Method 1 to be a bit time-consuming. If so, I think you’ll enjoy this method. I certainly wish my teachers had heard of it when I was in high school. Maybe they explained it and I was sleeping that day.
The second method is called the cross-product method. To use it, you compare the cross-products of two fractions. The first cross-product is the product of the first numerator and the second denominator. The second cross-product is the product of the second numerator and the first denominator. If the cross-products are equal, the fractions are equivalent. If the first cross-product is larger, the first fraction is larger. If the second cross-product is larger, the second fraction is larger.
 Which of the following fractions is the largest:
Which of the following fractions is the largest: ![]() ,
, ![]() ,
, ![]() , or
, or ![]() ?
?
Compare the first two fractions, ![]() and
and ![]() :
: ![]() and
and ![]() . The second fraction is larger.
. The second fraction is larger.
Compare the larger fraction, ![]() , with the third fraction,
, with the third fraction, ![]() :
: ![]() and
and ![]() , so
, so ![]() is still the largest fraction.
is still the largest fraction.
Now compare ![]() to the final fraction,
to the final fraction, ![]() :
: ![]() and
and ![]() .
.
The final fraction, ![]() , is the largest.
, is the largest.
Getting rational about ratios
Ratios represent how one quantity is related to another quantity. A ratio may be written as A:B or ![]() or using the phrase “A to B.”
or using the phrase “A to B.”
A ratio of 1:3 says that the second quantity is three times as large as the first. A ratio of 2:3 means that the second quantity is three times as large as one-half of the first quantity. A ratio of 5:4 means the second quantity is four times as large as one-fifth of the first quantity.
A ratio is actually a fraction. For example, the fraction ![]() is also a ratio of 3 to 4. Solve problems including ratios the same way you solve problems that include fractions.
is also a ratio of 3 to 4. Solve problems including ratios the same way you solve problems that include fractions.
Dealing with Decimals
Decimals are a method of writing fractional numbers without using a numerator and denominator. You can write the fraction ![]() as the decimal 0.7; you pronounce it “seven-tenths” or “zero point seven.” The period or decimal point indicates that the number is a decimal.
as the decimal 0.7; you pronounce it “seven-tenths” or “zero point seven.” The period or decimal point indicates that the number is a decimal.
Other decimals exist, such as hundredths or thousandths. They’re all based on the number ten:
- 0.7: Seven-tenths
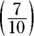
- 0.07: Seven-hundredths
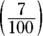
- 0.007: Seven-thousandths
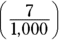
- 0.0007: Seven-ten-thousandths
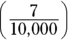
- 0.00007: Seven-hundred-thousandths
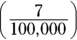 .
.
If a decimal is less than 1, it’s traditional in mathematics to place a zero before the decimal point. Write “0.7,” not “.7.”
A decimal may be greater than 1. The decimal 3.7 would be pronounced as “three and seven-tenths” ![]() .
.
Converting decimals to fractions
To convert a decimal to a fraction, write all the digits following the decimal point in the numerator. If you see zeros before any nonzero digits, you can ignore them.
The denominator is always a one followed by zeros. The number of zeros in the denominator is determined by the total number of digits to the right of the decimal point (including the leading zeros):
- One digit: Denominator = 10. Example:

- Two digits: Denominator = 100. Example:
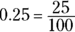
- Three digits: Denominator = 1,000. Example:
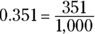
- Four digits: Denominator = 10,000. Example:
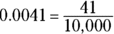
If necessary, reduce the fraction (see the earlier section “Simplifying fractions”).
Of course, you can also convert fractions to decimals (see the “Converting fractions to decimals” section earlier in this chapter).
Adding and subtracting decimals
You add and subtract decimals just as you do regular numbers (integers), except that before you perform your operation, you arrange the numbers in a column with the decimal points lined up one over the other.
 Add the numbers 3.147, 148.392, and 0.074.
Add the numbers 3.147, 148.392, and 0.074.
Put the numbers in an addition column with the decimal points lined up and perform the addition:

Multiplying decimals
Multiplying decimals requires three steps:
- Convert the decimals to whole numbers by moving the decimal points to the right, remembering to count how many spaces you move each decimal point.
- Multiply the whole numbers just as you’d perform any other multiplication.
- Place the decimal point in the product by moving the decimal point to the left the same number of total spaces you moved the decimal points to the right at the beginning.
 Multiply:
Multiply: ![]() .
.
First, convert the decimals to whole numbers by moving the decimal points to the right (remember to count).
- 3.724 becomes 3,724 (decimal moved three spaces).
- 0.0004 becomes 4 (decimal moved four spaces).
- 9.42 becomes 942 (decimal moved two spaces).
Next, perform the multiplication on the whole numbers:
Finally, put the decimal point in the correct position by moving it to the left the same number of places you moved the points to the right. You moved the decimal points a total of nine spaces to the right at the beginning, so now place the decimal point nine spaces to the left:
 If you run out of numbers before you’re finished counting spaces to the left, add zeros (as shown in the example) until you’ve finished counting.
If you run out of numbers before you’re finished counting spaces to the left, add zeros (as shown in the example) until you’ve finished counting.
Dividing decimals
Dividing decimals can be a challenge. You have to use both subtraction and multiplication. You also need to be pretty good at rounding (see the later “Rounding” section) and estimating numbers.
You can divide decimals in two ways: long division and conversion.
Method 1: Long division
To do long division with decimals, follow these steps:
- If the divisor isn’t a whole number, move the decimal point in the divisor all the way to the right (to make it a whole number), and move the decimal point in the dividend the same number of places to the right.
- Position the decimal point in the result directly above the decimal point in the dividend.
-
Divide as usual.
If the divisor doesn’t go into the dividend evenly, add zeros to the right of the last digit in the dividend and keep dividing until it comes out evenly or a repeating pattern shows up.
Try the following division problem:

![]()
Write the problem on your scratch paper in long-division form:
Now move the decimal point one place to the right, which makes the divisor a whole number. Also move the decimal point in the dividend one place to the right:
Position the decimal point in the result directly above the decimal point in the dividend:
Divide as usual. Seven goes into 70 ten times with 4 left over; then drop the 2 down:
Seven goes into 42 six times:
Method 2: Conversion
Try the problem from the preceding section, using the conversion method.

![]()
First, convert the decimals to fractions:
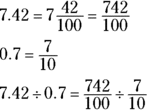
Take the reciprocal of the divisor (flip the second fraction upside down) and then multiply:
The fraction ![]() can be simplified (see “Simplifying fractions”) to
can be simplified (see “Simplifying fractions”) to ![]() . Convert
. Convert ![]() to a decimal (see “Converting fractions to decimals”), and the answer is 10.6.
to a decimal (see “Converting fractions to decimals”), and the answer is 10.6.
Rounding
Rounding a number means limiting a number to a few (or no) decimal places. For example, if you have a $1.97 in change in your pocket, you may say, “I have about $2.” The rounding process simplifies mathematical operations.
To round a number, you first determine what place you’re rounding to. For example, the math subtests that make up the AFQT may ask you to round to the nearest tenth. Then look at the number immediately to the right of that place. If the number is 5 or greater, round the digit to the left up; for any number under 5, round the digit to the left down. Thus, you’d round 1.55 up to 1.6 and 1.34 down to 1.3.
Perusing percents
Percent literally means “part of 100.” That means, for example, that 25 percent (25%) is equal to ![]() , which is equal to 0.25.
, which is equal to 0.25.
If a problem asks you to find 25 percent of 250, it’s asking you to multiply 250 by 0.25.
Playing with Positive and Negative Numbers
Numbers can be positive or negative. A positive number is any number greater than zero. So 4; 3.2; 793; ![]() ;
; ![]() ; and 430,932,843,784 are all positive numbers.
; and 430,932,843,784 are all positive numbers.
Numbers smaller than zero are negative numbers. Every positive number has a negative number equivalent. You express negative numbers by putting a negative (minus) sign (–) in front of the number: –7, –18, ![]() , and –743.42 are all negative numbers.
, and –743.42 are all negative numbers.
In the math subtests of the ASVAB, you’ll often be asked to perform mathematical operations on positive and negative numbers. Just remember the following rules:
- Adding two positive numbers always results in a positive number:
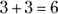
- Adding two negative numbers always results in a negative number:
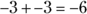
- Adding a negative number is the same as subtracting a positive number:

- Subtracting a negative number is the same as adding a positive number:

- Multiplying or dividing two positive numbers always results in a positive number:

- Multiplying or dividing two negative numbers always results in a positive number:
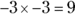
- Multiplying or dividing a negative number by a positive number always results in a negative number:
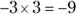
As you’ll recall from your math in school, any number multiplied by zero is zero.
Rooting for Roots and Powers
Many of the problems you see on the ASVAB math subtests require you to perform calculations involving roots, such as square roots and cube roots, and numbers raised to exponents. If that sounds confusing, don’t worry; it’s really not. Read on.
Advice about exponents
Exponents are an easy way to show that a number is to be multiplied by itself a certain number of times. For example, ![]() is the same as
is the same as ![]() , and
, and ![]() is the same as
is the same as ![]() . The number or variable that is to be multiplied by itself is called the base, and the number or variable showing how many times it’s to be multiplied by itself is called the exponent.
. The number or variable that is to be multiplied by itself is called the base, and the number or variable showing how many times it’s to be multiplied by itself is called the exponent.
Here are important rules when working with exponents:
- Any base raised to the power of 1 equals itself. For example,
 .
. -
Any base raised to the zero power (except 0) equals 1. For example,
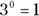 .
. In case you were wondering, according to most calculus textbooks,
In case you were wondering, according to most calculus textbooks, 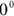 is an “indeterminate form.” What mathematicians mean by “indeterminate form” is that in some cases it has one value, and in other cases it has another. This stuff is advanced calculus, however, and you don’t have to worry about it on the ASVAB math subtests.
is an “indeterminate form.” What mathematicians mean by “indeterminate form” is that in some cases it has one value, and in other cases it has another. This stuff is advanced calculus, however, and you don’t have to worry about it on the ASVAB math subtests. - To multiply terms with the same base, you add the exponents. For example,
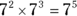 .
. - To divide terms with the same base, you subtract the exponents. For example,
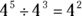 .
. - If a base has a negative exponent, it’s equal to its reciprocal with a positive exponent. For example,
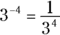 .
. - When a product has an exponent, each factor is raised to that power. For example,
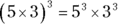 .
.
Roots
A root is the opposite of a power or an exponent. There are infinite kinds of roots. You have the square root, which means “undoing” a base to the second power; the cube root, which means “undoing” a base raised to the third power; a fourth root, for numbers raised to the fourth power; and so on. However, on the ASVAB math subtests, the only questions you’re likely to see will involve square roots and possibly a couple of cube roots.
Square roots
A math operation requiring you to find a square root is designated by the radical symbol ![]() . The number underneath the radical line is called the radicand. For example, in the operation
. The number underneath the radical line is called the radicand. For example, in the operation ![]() , the number 36 is the radicand.
, the number 36 is the radicand.
A square root is a number that, when multiplied by itself, produces the radicand. Take the square root of 36 ![]() , for example. If you multiply 6 by itself
, for example. If you multiply 6 by itself ![]() , you come up with 36, so 6 is the square root of 36.
, you come up with 36, so 6 is the square root of 36.
However, as I mention in the earlier section “Playing with Positive and Negative Numbers,” when you multiply two negative numbers together, you get a positive number. For example, ![]() also equals 36, so –6 is also the square root of 36.
also equals 36, so –6 is also the square root of 36.
That brings me to an important rule: When you take a square root, the results include two square roots — one positive and one negative.
There are two types of square roots:
- Perfect squares: Only some numbers, called perfect squares, have exact square roots.
- Irrational numbers: All the rest of the numbers have square roots that include decimals that go on forever and have no pattern that repeats (non-repeating, non-terminating decimals), so they’re called irrational numbers.
PERFECT SQUARES
Finding a square root can be difficult without a calculator, but because you can’t use a calculator during the test, you’re going to have to use your mind and some guessing methods. To find the square root of a number without a calculator, make an educated guess and then verify your results.
The radical symbol indicates that you’re to find the principal square root of the number under the radical. The principal square root is a positive number. But if you’re solving an equation such as ![]() , then you give both the positive and negative roots: 6 and –6.
, then you give both the positive and negative roots: 6 and –6.
To use the educated-guess method, you have to know the square roots of a few perfect squares. One good way to do so is to study the squares of the numbers 1 through 12:
- 1 and –1 are both square roots of 1.
- 2 and –2 are both square roots of 4.
- 3 and –3 are both square roots of 9.
- 4 and –4 are both square roots of 16.
- 5 and –5 are both square roots of 25.
- 6 and –6 are both square roots of 36.
- 7 and –7 are both square roots of 49.
- 8 and –8 are both square roots of 64.
- 9 and –9 are both square roots of 81.
- 10 and –10 are both square roots of 100.
- 11 and –11 are both square roots of 121.
- 12 and –12 are both square roots of 144.
IRRATIONAL NUMBERS
When the ASVAB asks you to figure square roots of numbers that don’t have perfect squares, the task gets a bit more difficult. If you have to find the square root of a number that isn’t a perfect square, the ASVAB usually asks you to find the square root to the nearest tenth.
Suppose you run across this problem:

![]()
Think about what you know:
- The square root of 49 is 7, and 54 is slightly greater than 49. You also know that the square root of 64 is 8, and 54 is slightly less than 64. (If you didn’t know that, check out the preceding section.)
- If the number 54 is somewhere between 49 and 64, the square root of 54 is somewhere between 7 and 8.
- Because 54 is closer to 49 than to 64, the square root will be closer to 7 than to 8, so you can try 7.3 as the square root of 54:
-
Multiply 7.3 by itself.
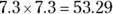 , which is very close to 54.
, which is very close to 54. -
Try multiplying 7.4 by itself to see whether it’s any closer to 54.
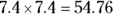 , which isn’t as close to 54 as 53.29.
, which isn’t as close to 54 as 53.29. - 7.3 is the square root of 54 to the nearest tenth.
-
Cube roots
A cube root is a number that when multiplied by itself three times equals the number under the radical. For example, the cube root of 27 is 3 because ![]() . A cube root is expressed by the radical sign with a 3 written on the left of the radical. For example, the cube root of 27 would be expressed as
. A cube root is expressed by the radical sign with a 3 written on the left of the radical. For example, the cube root of 27 would be expressed as ![]() .
.
Each number has only one cube root (unlike square roots). If the radicand is positive, the cube root will be a positive number.
Also, unlike with square roots, finding the cube root of a negative number without involving advanced mathematics is possible. If the radicand is negative, the cube root will also be negative. For example, ![]() .
.
Just like square roots, you should memorize a few common cube roots:
- 1 is the cube root of 1, and –1 is the cube root of –1.
- 2 is the cube root of 8, and –2 is the cube root of –8.
- 3 is the cube root of 27, and –3 is the cube root of –27.
- 4 is the cube root of 64, and –4 is the cube root of –64.
- 5 is the cube root of 125, and –5 is the cube root of –125.
- 6 is the cube root of 216, and –6 is the cube root of –216.
- 7 is the cube root of 343, and –7 is the cube root of –343.
- 8 is the cube root of 512, and –8 is the cube root of –512.
- 9 is the cube root of 729, and –9 is the cube root of –729.
- 10 is the cube root of 1,000, and –10 is the cube root of –1,000.
Scientific notation
Scientific notation is a compact format for writing very large or very small numbers. Although it’s most often used in scientific fields, you may find a question or two on the Mathematics Knowledge subtest of the ASVAB asking you to convert a number to scientific notation, or vice versa.
Scientific notation separates a number into two parts: a characteristic, which is always greater than or equal to 1 and less than 10, and a power of ten. Thus, ![]() means 1.25 times 10 to the fourth power, or 12,500;
means 1.25 times 10 to the fourth power, or 12,500; ![]() means 5.79 times 10 to the negative eighth power. (Remember that a negative exponent is equal to its reciprocal with a positive exponent, so
means 5.79 times 10 to the negative eighth power. (Remember that a negative exponent is equal to its reciprocal with a positive exponent, so ![]() means
means ![]() ). In this case, the scientific notation comes out to 0.0000000579.
). In this case, the scientific notation comes out to 0.0000000579.
Alphabet Soup: Tackling Algebra Review
Algebra problems are equations, which means that the quantities on both sides of the equal sign are equal — they’re the same: ![]() ,
, ![]() , and
, and ![]() . In all these cases, the quantities are the same on both sides of the equal sign. So, if
. In all these cases, the quantities are the same on both sides of the equal sign. So, if ![]() , then x is 2 because the equal sign says so.
, then x is 2 because the equal sign says so.
Visiting variables
Most algebraic equations involve using one or more variables. A variable is a symbol that represents a number. Usually, algebra problems use letters such as n, t, or x for variables. In most algebra problems, your goal is to find the value of the variable. For example, in the equation ![]() , you’d try to find the value of x by using the rules of algebra.
, you’d try to find the value of x by using the rules of algebra.
Following the rules of algebra
Algebra has several rules or properties that — when combined — allow you to simplify equations. Some (but not all) equations can be simplified to a complete solution:
- You may combine like terms. This rule means adding or subtracting terms with variables of the same kind. The expression
 simplifies to 8x.
simplifies to 8x. 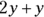 is equal to 3y. The expression
is equal to 3y. The expression 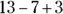 simplifies to 9.
simplifies to 9. - You may use the distributive property to remove parentheses around unlike terms (see “The distributive property: Breaking up large numbers” earlier in this chapter).
- You may add or subtract any value as long as you do it to both sides of the equation.
- You may multiply or divide by any number (except 0) as long as you do it to both sides of the equation.
Combining like terms
One of the most common ways to simplify an expression is to combine like terms. Numeric terms may be combined, and any terms with the same variable part may be combined.
Take, for instance, the expression ![]() .
.
5x and 3x are like terms. So are –6y and 7y. 3 and 4 are also like terms because they’re numbers without variables. By combining the like terms, you get

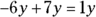 (or just y)
(or just y)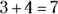
By combining the like terms, the expression ![]() simplifies to
simplifies to ![]() .
.
Using the distributive property
I know what you’re thinking: Combining like terms is pretty cool, but what if you have unlike terms contained within parentheses? Doesn’t the order of operations require you to deal with terms in parentheses first? Indeed, it does, and that’s where the distributive property comes in.
As I explain earlier in the chapter, ![]() . For example,
. For example, ![]() is mathematically the same as
is mathematically the same as ![]() .
.
Applying the same principle to algebra, the distributive property can be very useful in getting rid of those pesky parentheses:
Using addition and subtraction
You can use addition and subtraction to get all the terms with variables on one side of an equation and all the numeric terms on the other. That’s an important step in finding the value of the variable.
The equation ![]() has only the variable term on one side and only a number on the other. The equation
has only the variable term on one side and only a number on the other. The equation ![]() doesn’t.
doesn’t.
The equation simplifies to ![]() .
.
Using multiplication and division
The rules of algebra also allow you to multiply and divide both sides of an equation by any number except zero. Say you have an equation that reads ![]() , or 3 times x equals 21. You want to find the value of x, not three times x.
, or 3 times x equals 21. You want to find the value of x, not three times x.
What happens if you divide a number by itself? The result is 1. Therefore, to change 3x to 1x (or x), divide both sides of the equation by 3:
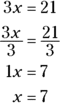
But what if the equation were ![]() ? What would you do then?
? What would you do then?
I’ll give you a hint: If you multiply any fraction by its reciprocal, the result is 1. Remember, a reciprocal is a fraction flipped upside down.

Remember to multiply both sides of the equation by ![]() .
.
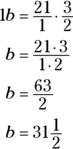
All Is Not Equal: Examining Inequalities
Earlier in the chapter, I say that all equations include equal signs (=), and I stand by that statement. After all, I wouldn’t lie to you. However, some math problems look very much like equations, but they use signs other than the equal sign.
These problems are called inequalities. An equation states that each side of the equation separated by the equal sign is equal to the other. An inequality, on the other hand, says that the two sides separated by an inequality sign are not equal to each other.
Just as with equations, the solution to an inequality is all the values that make the inequality true. For the most part, you solve inequalities the same as you’d solve a normal equation. You need to keep some facts of inequality life in mind, however. Short and sweet, here they are:
- Negative numbers are less than zero and less than positive numbers.
- Zero is less than positive numbers but greater than negative numbers.
- Positive numbers are greater than negative numbers and greater than zero.
Although there’s only one equal sign (=), several signs are associated with inequalities:
 means does not equal in the way that 3 does not equal 4, or
means does not equal in the way that 3 does not equal 4, or 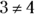 .
.- > means greater than in the way that 4 is greater than 3, or
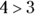 .
. - < means less than in the way the 3 is less than 4, or
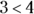 .
. 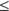 means less than or equal to in the way that x may be less than or equal to 4, or
means less than or equal to in the way that x may be less than or equal to 4, or 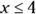 .
.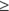 means greater than or equal to in the way that x may be greater than or equal to 3, or
means greater than or equal to in the way that x may be greater than or equal to 3, or 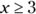 .
.
You solve inequalities by using the same principles of algebra used to solve equations, with the exception of multiplying or dividing each side by a negative number (check out the earlier “Following the rules of algebra” section). Take the following example:
 Solve:
Solve: ![]() .
.
The inequality says that 3x plus 4 is less than 25. You solve it in the same way as you would the equation ![]() :
:
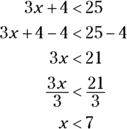
- In algebra, if
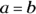 , then
, then 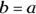 . In other words, you can swap the data on each side of the equal sign, and the equation means the same thing. So
. In other words, you can swap the data on each side of the equal sign, and the equation means the same thing. So  and
and 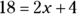 are the same thing. This interchangeability doesn’t work with inequalities. In other words,
are the same thing. This interchangeability doesn’t work with inequalities. In other words, 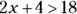 isn’t the same as
isn’t the same as 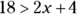 . When you swap the data in an inequality, you have to change the inequality sign to balance the inequality (keep the inequity true). So
. When you swap the data in an inequality, you have to change the inequality sign to balance the inequality (keep the inequity true). So 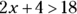 is the same as
is the same as 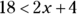 .
. - When you multiply or divide both sides of the inequality by a negative number, the inequality sign is reversed. That means if you multiply both sides of the inequality
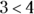 by –4, your answer is
by –4, your answer is 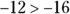 .
.
Solving Quadratics
A quadratic equation is an algebraic equation in which the unknown is raised to an exponent of 2 (and no higher), as in ![]() . Quadratic equations can be very simple or very complex (or several degrees of difficulty in between). Here are some examples:
. Quadratic equations can be very simple or very complex (or several degrees of difficulty in between). Here are some examples:
You can solve quadratics in three primary ways: the square-root method, factoring, or the quadratic formula. Which method you choose depends on the difficulty of the equation.
Method 1: The square-root method
Simple quadratic equations (those that consist of just one squared term and a number) can be solved by using the square-root rule:
If
, then
, as long as k isn’t a negative number.
Remember to include the ![]() sign, which indicates that the answer is a positive or negative number. Take the following simple quadratic equation:
sign, which indicates that the answer is a positive or negative number. Take the following simple quadratic equation:
 Solve:
Solve: ![]() .
.
-
First, isolate the variable by subtracting 4 from each side.
The result is
 .
. -
Next, get rid of the 3 by dividing both sides of the equation by 3.
The result is
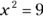 .
. -
You can now solve by using the square root rule.
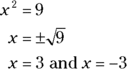
Method 2: The factoring method
Most quadratic equations you encounter on the ASVAB math subtests can be solved by putting the equation into the quadratic form and then factoring.
The quadratic form is ![]() , where a, b, and c are just numbers. All quadratic equations can be expressed in this form. Want to see some examples?
, where a, b, and c are just numbers. All quadratic equations can be expressed in this form. Want to see some examples?
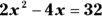 : This equation can be expressed in the quadratic form as
: This equation can be expressed in the quadratic form as  . In this case,
. In this case, 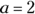 ,
, 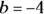 , and
, and 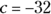 .
.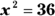 : You can express this equation as
: You can express this equation as 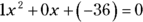 . So
. So 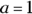 ,
, 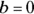 , and
, and 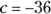 .
.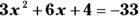 : Expressed in quadratic form, this equation reads
: Expressed in quadratic form, this equation reads 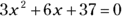 . So
. So 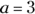 ,
,  , and
, and 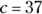 .
.
Ready to factor? How about trying the following equation?
 Solve:
Solve: ![]() .
.
Because I like you, I’ve already expressed the equation in quadratic form (the expression on the left is equal to zero), saving you a little time.
 You can use the factoring method for most quadratic equations where
You can use the factoring method for most quadratic equations where ![]() and c is a positive number.
and c is a positive number.
The first step in factoring a quadratic equation is to draw two sets of parentheses on your scratch paper, and then place an x at the front of each, leaving some extra space after it. As with the original quadratic, the equation should equal zero:
The next step is to find two numbers that equal c when multiplied together and equal b when added together. In the example equation, ![]() and
and ![]() , so you need to hunt for two numbers that multiply to 6 and add up to 5. For example,
, so you need to hunt for two numbers that multiply to 6 and add up to 5. For example, ![]() and
and ![]() . In this case, the two numbers you’re seeking are positive 2 and positive 3.
. In this case, the two numbers you’re seeking are positive 2 and positive 3.
Finally, put these two numbers into your set of parentheses:
Any number multiplied by zero equals zero, which means that ![]() and/or
and/or ![]() . The solution to this quadratic equation is
. The solution to this quadratic equation is ![]() and/or
and/or ![]() .
.
- If c is positive, then the factors you’re looking for are either both positive or both negative:
- If b is positive, then the factors are positive.
- If b is negative, then the factors are negative.
- b is the sum of the two factors that give you c.
- If c is negative, then the factors you’re looking for are of alternating signs; that is, one is negative and one is positive:
- If b is positive, then the larger factor is positive.
- If b is negative, then the larger factor is negative.
- b is the difference between the two factors that gives you c.
Try another one, just for giggles:
 Solve:
Solve: ![]() .
.
Start by writing your parentheses:
In this equation, ![]() and
and ![]() . Because b is negative and c is positive, both factors will be negative.
. Because b is negative and c is positive, both factors will be negative.
You’re looking for two negative numbers that multiply to 6 and add to –7. Those numbers are –1 and –6. Plugging the numbers into your parentheses, you get ![]() . That means
. That means ![]() and/or
and/or ![]() .
.
Method 3: The quadratic formula
The square-root method can be used for simple quadratics, and the factoring method can easily be used for many other quadratics, as long as ![]() . (See the two preceding sections.) But what if a doesn’t equal 1, or you can’t easily find two numbers that multiply to c and add up to b?
. (See the two preceding sections.) But what if a doesn’t equal 1, or you can’t easily find two numbers that multiply to c and add up to b?
You can use the quadratic formula to solve any quadratic equation. So why not just use the quadratic formula and forget about the square-root and factoring methods? Because the quadratic formula is kind of complex:
The quadratic formula uses the a, b, and c from ![]() , just like the factoring method.
, just like the factoring method.
Armed with this knowledge, you can apply your skills to a complex quadratic equation:
 Solve:
Solve: ![]() .
.
In this equation, ![]() ,
, ![]() , and
, and ![]() . Plug the known values into the quadratic formula and simplify:
. Plug the known values into the quadratic formula and simplify:
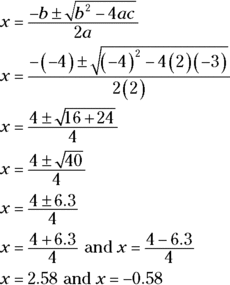
Rounded to the nearest tenth, ![]() and
and ![]() .
.
Knowing All the Angles: Geometry Review
According to my handy pocket dictionary, geometry is “the branch of mathematics that deals with the deduction of the properties, measurement, and relationships of points, lines, angles, and figures in space from their defining conditions by means of certain assumed properties of space.” Sounds interesting!
Really, geometry is simply the branch of mathematics that’s concerned with shapes, lines, and angles. From the perspective of the ASVAB math subtests, you should be able to identify basic geometric shapes and know certain properties about them so you can determine their angles and measurements. You see a lot of geometry-related questions on both the Mathematics Knowledge and the Arithmetic Reasoning subtests of the ASVAB.
Knowing all the angles
Angles are formed when two lines intersect at a point. Many geometric shapes are formed by intersecting lines, which form angles. Angles can be measured in degrees. The greater the number of degrees, the wider the angle is:
- A straight line is exactly 180°.
- A right angle is exactly 90°.
- An acute angle is more than 0° and less than 90°.
- An obtuse angle is more than 90° but less than 180°.
- Complementary angles are two angles that equal 90° when added together.
- Supplementary angles are two angles that equal 180° when added together.
Take a look at the different types of angles in Figure 9-3.
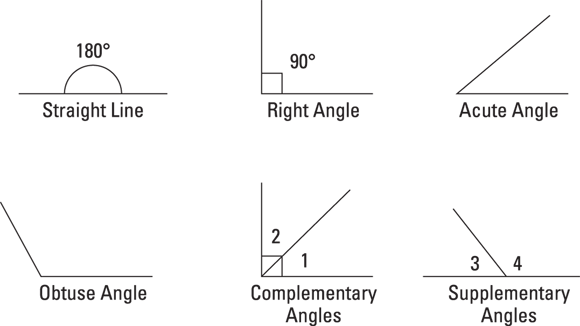
© John Wiley & Sons, Inc.
FIGURE 9-3: Types of angles.
Common geometric shapes
I’m not going to explain all the possible geometric shapes for two reasons: Doing so would take this entire book, and you don’t need to know them all to solve the math problems you find on the ASVAB. However, you should recognize the most common shapes associated with geometry.
Getting square with quadrilaterals
A quadrilateral is a geometric shape with four sides. All quadrilaterals contain interior angles totaling 360°. Here are the five most common types of quadrilaterals:
- Squares have four sides of equal length, and all the angles are right angles.
- Rectangles have all right angles.
- Rhombuses have four sides of equal length, but the angles don’t have to be right angles.
- Trapezoids have at least two sides that are parallel.
- Parallelograms have opposite sides that are parallel, and their opposite sides and angles are equal.
Figure 9-4 gives you an idea of what these five quadrilaterals look like.

© John Wiley & Sons, Inc.
FIGURE 9-4: Common quadrilaterals.
Trying out triangles
A triangle consists of three straight lines whose three interior angles always add up to 180°. The sides of a triangle are called legs. Triangles can be classified according to the relationship among their angles, the relationship among their sides, or some combination of these relationships. You should know the three most common types of triangles:
- Isosceles triangle: Has two equal sides, and the angles opposite the equal sides are also equal.
- Equilateral triangle: Has three equal sides, and all the angles measure 60°.
- Right triangle: Has one right angle (90°); therefore, the remaining two angles are complementary (add up to 90°). The side opposite the right angle is called the hypotenuse, which is the longest side of a right triangle.
Check out Figure 9-5 to see what these triangles look like.
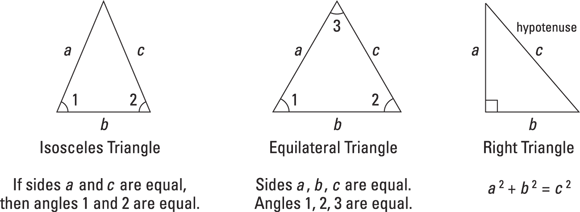
© John Wiley & Sons, Inc.
FIGURE 9-5: The three most common types of triangles.
Settling on circles
A circle is formed when the points of a closed line are all located equal distances from a point called the center of the circle. A circle always has 360°. The closed line of a circle is called its circumference. The radius of a circle is the measurement from the center of the circle to any point on the circumference of the circle. The diameter of the circle is measured as a line passing through the center of the circle, from a point on one side of the circle to a point on the other side of the circle. The diameter of a circle is always twice as long as the radius. Figure 9-6 shows these relationships.
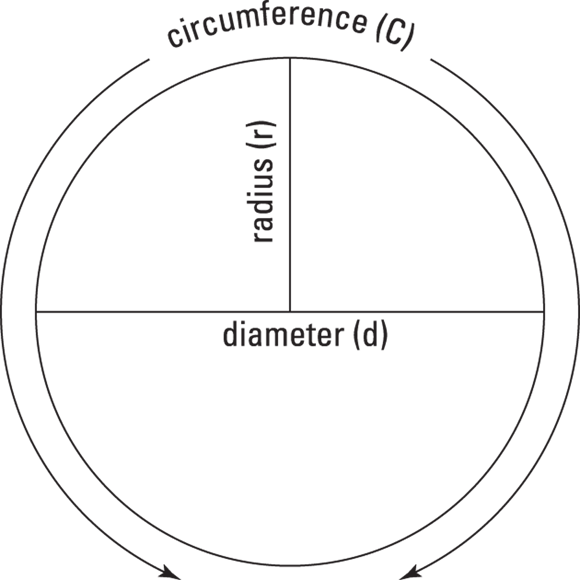
© John Wiley & Sons, Inc.
FIGURE 9-6: The parts of a circle.
Famous geometry formulas
The math subtests of the ASVAB often ask you to use basic geometry formulas to calculate geometric measurements. You should commit these simple formulas to memory.
Quadrilateral formulas you should know
You may be asked to calculate the perimeter (distance around), the area, or the diagonal of a square or rectangle. Use the following formulas:
- Perimeter of a square:
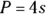 , where
, where 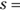 one side of the square
one side of the square - Area of a square:
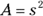
- Diagonal of a square:
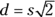
- Perimeter of a rectangle:
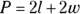 , where
, where 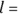 the length and
the length and 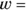 the width of the rectangle; you can also write this formula as
the width of the rectangle; you can also write this formula as 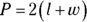
- Area of a rectangle:
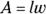
- Diagonal of a rectangle:
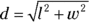
Good-to-know triangle formulas
Some math problems on the ASVAB may ask you to calculate the perimeter or area of a triangle. The following formulas are used for these two purposes:
- Perimeter of a triangle:
 , where
, where 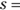 the length of each side of the triangle
the length of each side of the triangle - Area of a triangle:
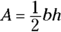 , where
, where  the length of the triangle’s base (bottom) and
the length of the triangle’s base (bottom) and 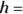 the height of the triangle
the height of the triangle
Circle formulas
Circles are a bit more complex than squares, rectangles, and triangles and often involve invoking the value of ![]() . In the “Making the Most of Math Terminology” section earlier in this chapter, I tell you that
. In the “Making the Most of Math Terminology” section earlier in this chapter, I tell you that ![]() is approximately equal to 3.14.
is approximately equal to 3.14.
- Radius of a circle:
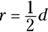 , where
, where 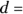 the diameter of the circle
the diameter of the circle - Diameter of a circle:
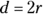
- Circumference of a circle:
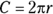
- Area of a circle:

Handy formulas for three-dimensional shapes
Sometimes the math subtests require you to calculate measurements for solid (three-dimensional) shapes. These types of questions generally come in two flavors: calculating volume or calculating surface area.
Volume is the space a shape takes up. You can think of volume as how much a shape would hold if you poured water into it. Surface area is the area of the outside of the shape — for example, the amount of area you’d have to cover if you were to paint the outside of the solid shape.
- Volume of a cube:
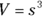 , where
, where 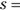 the length of one side of the cube
the length of one side of the cube - Volume of a box (also called a rectangular prism):
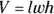 , where
, where  the length,
the length, 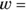 the width, and
the width, and 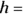 the height of the box
the height of the box - Volume of a cylinder:
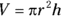 , where
, where 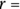 the radius of the cylinder and
the radius of the cylinder and 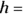 the height of the cylinder
the height of the cylinder - Surface area of a cube:
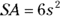
- Surface area of a box (rectangular prism):
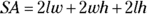
You Got a Problem? Math Knowledge Exercises
The best way to get better at math is to practice, and I couldn’t let you leave this chapter without giving you a few run-throughs on the material you just read. These exercises are designed to help you flex your math muscles. You’ll practice terminology (I promise not to quiz you on the word brachistochrone), run around with Dear Aunt Sally, and convert fractions. You’ll also keep equations balanced and identify which formulas you should use to solve problems on the ASVAB.
Math terminology practice
Remember when your mother said, “It’s not what you say; it’s how you say it”? She wasn’t talking about math. In mathematics, it’s exactly what you say that matters. Use Activity 1 to match the signal words to the correct mathematical operations (addition, subtraction, multiplication, or division), and then check the “Answers and Explanations” section at the end of this chapter to make sure you’re right.
ACTIVITY 1 Math Terminology
Signal Word |
Operation (addition, subtraction, multiplication, or division) |
1. Increase |
|
2. Deduct |
|
3. Product |
|
4. Quotient |
|
5. Sum |
|
6. Of |
|
7. Difference |
|
8. Total |
|
9. Less |
|
10. By |
Order of operations practice
Math is a lot like the military: There are right ways and wrong ways to do everything. In mathematics, it’s all about the order of operations. Remember that Aunt Sally — although we always have to apologize for her (Please Excuse My Dear Aunt Sally) — can show you how to solve any math problem in the right order (refer back to “Obeying the order of operations,” earlier in this chapter). In Activity 2, look at the problem and determine which operations you’ll do first, then which you’ll do second. You don’t need to perform the calculations. When you’re done, see whether you’re right in the “Answers and Explanations” section at the end of this chapter. When you’re only simplifying things, it’s often okay to switch the first and second operations you perform.
ACTIVITY 2 Order of Operations
Problem |
First |
Second |
Example: |
|
Add 5, 6, and the product of 17 and 2 |
1. |
||
2. |
||
3. |
||
4. |
||
5. |
||
6. |
||
7. |
||
8. |
||
9. |
||
10. |
Converting fractions and decimals
When you run into an ASVAB question that contains fractions and decimals, you’ll most likely need to convert one or the other to solve the problem (see “Dealing with Decimals” earlier in this chapter). Use Activity 3 to practice switching between fractions and decimals, and then check the “Answers and Explanations” section at the end of this chapter to see how well you did.
ACTIVITY 3 Fractions and Decimals
Problem |
Your Conversion |
1. 0.17 |
|
2. |
|
3. |
|
4. 4.75 |
|
5. 18.925 |
|
6. |
|
7. |
|
8. 9.217 |
|
9. –37.2 |
|
10. |
Solving equations and inequalities
When you take the ASVAB, you’ll do plenty of mental math — but you’ll also use some of the unlimited supply of scratch paper the test proctor gives you to write equations. Simple errors in an equation can throw off your entire game, though, so use Activity 4 to practice solving each equation or inequality. When you’re finished, check your work in the “Answers and Explanations” section at the end of this chapter. (If you need to brush up on balancing equations, see the “Following the rules of algebra” section earlier in this chapter.)
ACTIVITY 4 Solving Equations and Inequalities
Problem |
Your Work |
1. |
|
2. |
|
3. |
|
4. |
|
5. |
Identifying formulas
Many of the algebra and geometry questions on the ASVAB require you to plumb the depths of your memory for a specific mathematical formula. If you can’t remember it, you’re going to have a tough time coming up with the right answer. Use Activity 5 to match each type of problem with the appropriate formula to solve it. (Note: Not all of these formulas appear in this chapter.) Make sure you connected the right pairs by checking your answers in the “Answers and Explanations” section at the end of this chapter.
ACTIVITY 5 Identifying Formulas
Answer |
Formula Type |
Formula |
1. |
1. Quadratic equation |
A. |
2. |
2. Pythagorean theorem |
B. |
3. |
3. Area of a triangle |
C. |
4. |
4. Area of a rectangle |
D. |
5. |
5. Circumference of a circle |
E. |
6. |
6. Slope-intercept form |
F. |
7. |
7. Distance traveled |
G. |
8. |
8. Simple interest |
H. |
9. |
9. Area of a circle |
I. |
10. |
10. Volume of a rectangular prism |
J. |
Answers and Explanations
Check your answers for each of the exercises here, and take some time to review the explanations if you’re not sure where you went wrong.
Activity 1: Math Terminology
- Increase: addition
- Deduct: subtraction
- Product: multiplication
- Quotient: division
- Sum: addition
- Of: multiplication
- Difference: subtraction
- Total: addition
- Less: subtraction
- By: multiplication
Activity 2: Order of Operations
Problem |
First |
Second |
1. |
|
|
2. |
|
|
3. |
|
add 27 |
4. |
|
multiply 182 by x |
5. |
|
divide by 4 |
6. |
|
add 12 |
7. |
|
add the remaining numbers |
8. |
|
divide by 2 |
9. |
|
add 17 |
10. |
|
divide by 2 |
Activity 3: Fractions and Decimals
Problem |
Your Conversion |
1. 0.17 |
|
2. |
0.4 |
3. |
1.3 |
4. 4.75 |
|
5. 18.925 |
|
6. |
2.625 |
7. |
11.2 |
8. 9.217 |
|
9. –37.2 |
|
10. |
18.125 |
Activity 4: Solving Equations and Inequalities
Activity 5: Identifying Formulas
- D. The quadratic equation is
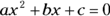 .
. - G. The Pythagorean theorem is
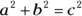 .
. - F. The formula to find the area of a triangle is
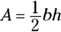 , where A represents area, b represents the length of the base, and h represents the triangle’s height.
, where A represents area, b represents the length of the base, and h represents the triangle’s height. - A. The formula to find the area of a rectangle is
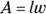 , where A represents area, l represents the rectangle’s length, and w represents the rectangle’s width.
, where A represents area, l represents the rectangle’s length, and w represents the rectangle’s width. - E. The formula to find the circumference (the distance around) a circle is
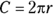 , where C represents circumference and r represents the circle’s radius (the distance from the center of the circle to its outer edge).
, where C represents circumference and r represents the circle’s radius (the distance from the center of the circle to its outer edge). - J. The formula for slope-intercept form of a line is
 , where m is the slope and b is the y-intercept. In this formula, x and y represent coordinate points.
, where m is the slope and b is the y-intercept. In this formula, x and y represent coordinate points. - B. The formula to find distance traveled is
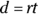 , where d represents distance, r represents rate (speed), and t represents time.
, where d represents distance, r represents rate (speed), and t represents time. - I. The formula to figure out simple interest is
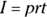 , where I represents interest, p represents principal, r represents the rate of interest per year expressed as a decimal, and t represents the time periods involved.
, where I represents interest, p represents principal, r represents the rate of interest per year expressed as a decimal, and t represents the time periods involved. - C. The formula to find the area of a circle is
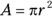 , where A represents area and r represents the circle’s radius (the distance, in a straight line, from the circle’s center to its outer edge).
, where A represents area and r represents the circle’s radius (the distance, in a straight line, from the circle’s center to its outer edge). - H. The formula to find the volume of a rectangular prism is
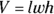 , where V represents volume, l represents length, w represents width, and h represents height.
, where V represents volume, l represents length, w represents width, and h represents height.