14
Construction of Empirical Models
14.1 The Empirical Distribution
The material presented here has traditionally been presented under the heading of “survival models,” with the accompanying notion that the techniques are useful only when studying lifetime distributions. Standard texts on the subject, such as Klein and Moeschberger [70] and Lawless [77], contain examples that are exclusively oriented in that direction. However, the same problems that occur when modeling lifetime occur when modeling payment amounts. The examples we present are of both types. However, the latter sections focus on special considerations when constructing decrement models. Only a handful of references are presented, most of the results being well developed in the survival models literature. If you want more detail and proofs, consult a text dedicated to the subject, such as the ones just mentioned.
In Chapter 4, models were divided into two types – data-dependent and parametric. The definitions are repeated here.
This chapter will focus on data-dependent distributions as models, making few, if any, assumptions about the underlying distribution. To fix the most important concepts, we begin by assuming that we have a sample of n observations that are an independent and identically distributed sample from the same (unspecified) continuous distribution. This is referred to as a complete data situation. In that context, we have the following definition.
When observations are collected from a probability distribution, the ideal situation is to have the (essentially) exact1 value of each observation. This case is referred to as complete, individual data and applies to Data Set B, introduced in Chapter 10 and reproduced here as Table 14.1. There are two reasons why exact data may not be available. One is grouping, in which all that is recorded is the range of values in which the observation belongs. Grouping applies to Data Set C and to Data Set A for those with five or more accidents. There data sets were introduced in Chapter 10 and are reproduced here as Tables 14.2 and 14.3, respectively.
Table 14.1 Data Set B.
| 27 | 82 | 115 | 126 | 155 | 161 | 243 | 294 | 340 | 384 |
| 457 | 680 | 855 | 877 | 974 | 1,193 | 1,340 | 1,884 | 2,558 | 15,743 |
Table 14.2 Data Set C.
| Payment range | Number of payments |
| 0–7,500 | 99 |
| 7,500–17,500 | 42 |
| 17,500–32,500 | 29 |
| 32,500–67,500 | 28 |
| 67,500–125,000 | 17 |
| 125,000–300,000 | 9 |
| Over 300,000 | 3 |
Table 14.3 Data Set A.
| Number of accidents | Number of drivers |
| 0 | 81,714 |
| 1 | 11,306 |
| 2 | 1,618 |
| 3 | 250 |
| 4 | 40 |
| 5 or more | 7 |
A second reason that exact values may not be available is the presence of censoring or truncation. When data are censored from below, observations below a given value are known to be below that value but the exact value is unknown. When data are censored from above, observations above a given value are known to be above that value but the exact value is unknown. Note that censoring effectively creates grouped data. When the data are grouped in the first place, censoring has no effect. For example, the data in Data Set C may have been censored from above at 300,000, but we cannot know for sure from the data set and that knowledge has no effect on how we treat the data. In contrast, were Data Set B to be censored at 1,000, we would have 15 individual observations and then five grouped observations in the interval from 1,000 to infinity.
In insurance settings, censoring from above is fairly common. For example, if a policy pays no more than 100,000 for an accident, any time the loss is above 100,000 the actual amount will be unknown, but we will know that it happened. Note that Data Set A has been censored from above at 5. This is more common language than saying that Data Set A has some individual data and some grouped data. When studying mortality or other decrements, the study period may end with some individuals still alive. They are censored from above in that we know the death will occur sometime after their age when the study ends.
When data are truncated from below, observations below a given value are not recorded. Truncation from above implies that observations above a given value are not recorded. In insurance settings, truncation from below is fairly common. If an automobile physical damage policy has a per-claim deductible of 250, any losses below 250 will not come to the attention of the insurance company and so will not appear in any data sets. Data sets may have truncation forced on them. For example, if Data Set B were to be truncated from below at 250, the first seven observations would disappear and the remaining 13 would be unchanged. In decrement studies it is unusual to observe individuals from birth. If someone is first observed at, say, age 20, that person is from a population where anyone who died before age 20 would not have been observed and thus is truncated from below.
As noted in Definition 14.3, the empirical distribution assigns probability 1/n to each data point. That definition works well when the value of each data point is recorded. An alternative definition follows.
![]()
In the following example, not all values are distinct.
![]()
To assess the quality of the estimate, we examine statistical properties, in particular, the mean and variance. Working with the empirical estimate of the distribution function is straightforward. To see that with complete data the empirical estimator of the survival function is unbiased and consistent, recall that the empirical estimate of ![]() is
is ![]() , where Y is the number of observations in the sample that are less than or equal to x. Then Y must have a binomial distribution with parameters n and
, where Y is the number of observations in the sample that are less than or equal to x. Then Y must have a binomial distribution with parameters n and ![]() and
and
demonstrating that the estimator is unbiased. The variance is
which has a limit of zero, thus verifying consistency.
To make use of the result, the best we can do for the variance is estimate it. It is unlikely that we will know the value of ![]() , because that is the quantity we are trying to estimate. The estimated variance is given by
, because that is the quantity we are trying to estimate. The estimated variance is given by
The same results hold for empirically estimated probabilities. Let ![]() . The empirical estimate of p is
. The empirical estimate of p is ![]() . Arguments similar to those used for
. Arguments similar to those used for ![]() verify that
verify that ![]() is unbiased and consistent, with
is unbiased and consistent, with ![]() .
.
![]()
14.2 Empirical Distributions for Grouped Data
For grouped data as in Data Set C, construction of the empirical distribution as defined previously is not possible. However, it is possible to approximate the empirical distribution. The strategy is to obtain values of the empirical distribution function wherever possible and then connect those values in some reasonable way. For grouped data, the distribution function is usually approximated by connecting the points with straight lines. For notation, let the group boundaries be ![]() , where often
, where often ![]() and
and ![]() . The number of observations falling between
. The number of observations falling between ![]() and
and ![]() is denoted
is denoted ![]() , with
, with ![]() . For such data, we are able to determine the empirical distribution at each group boundary. That is,
. For such data, we are able to determine the empirical distribution at each group boundary. That is, ![]() . Note that no rule is proposed for observations that fall on a group boundary. There is no correct approach, but whatever approach is used, consistency in assignment of observations to groups should be used. Note that in Data Set C it is not possible to tell how the assignments were made. If we had that knowledge, it would not affect any subsequent calculations.2
. Note that no rule is proposed for observations that fall on a group boundary. There is no correct approach, but whatever approach is used, consistency in assignment of observations to groups should be used. Note that in Data Set C it is not possible to tell how the assignments were made. If we had that knowledge, it would not affect any subsequent calculations.2
This function is differentiable at all values except group boundaries. Therefore the density function can be obtained. To completely specify the density function, it is arbitrarily made right continuous.
Many computer programs that produce histograms actually create a bar chart with bar heights proportional to ![]() . A bar chart is acceptable if the groups have equal width, but if not, then the preceding formula is needed. The advantage of this approach is that the histogram is indeed a density function and, among other things, areas under the histogram can be used to obtain empirical probabilities.
. A bar chart is acceptable if the groups have equal width, but if not, then the preceding formula is needed. The advantage of this approach is that the histogram is indeed a density function and, among other things, areas under the histogram can be used to obtain empirical probabilities.
![]()
14.2.1 Exercises
- 14.1 Construct the ogive and histogram for the data in Table 14.4.
Table 14.4 The data for Exercise 14.1.
Payment range Number of payments 0–25 6 25–50 24 50–75 30 75–100 31 100–150 57 150–250 80 250–500 85 500–1,000 54 1,000–2,000 15 2,000–4,000 10 Over 4,000 0 - 14.2 (*) The following 20 windstorm losses (in millions of dollars) were recorded in one year:

- Construct an ogive based on using class boundaries at 0.5, 2.5, 8.5, 15.5, and 29.5.
- Construct a histogram using the same boundaries as in part (a).
- 14.3 The data in Table 14.5 are from Herzog and Laverty [53]. A certain class of 15-year mortgages was followed from issue until December 31, 1993. The issues were split into those that were refinances of existing mortgages and those that were original issues. Each entry in the table provides the number of issues and the percentage of them that were still in effect after the indicated number of years. Draw as much of the two ogives (on the same graph) as is possible from the data. Does it appear from the ogives that the lifetime variable (the time to mortgage termination) has a different distribution for refinanced versus original issues?
Table 14.5 The data for Exercise 14.3.
Refinances Original Years Number issued Survived Number issued Survived 1.5 42,300 99.97 12,813 99.88 2.5 9,756 99.82 18,787 99.43 3.5 1,550 99.03 22,513 98.81 4.5 1,256 98.41 21,420 98.26 5.5 1,619 97.78 26,790 97.45 - 14.4 (*) The data in Table 14.6 were collected (the units are millions of dollars). Construct the histogram.
Table 14.6 The data for Exercise 14.4.
Loss Number of observations 0–2 25 2–10 10 10–100 10 100–1,000 5 - 14.5 (*) Forty losses have been observed. Sixteen losses are between 1 and
 (in millions), and the sum of the 16 losses is 20. Ten losses are between
(in millions), and the sum of the 16 losses is 20. Ten losses are between  and 2, with a total of 15. Ten more are between 2 and 4, with a total of 35. The remaining four losses are greater than 4. Using the empirical model based on these observations, determine
and 2, with a total of 15. Ten more are between 2 and 4, with a total of 35. The remaining four losses are greater than 4. Using the empirical model based on these observations, determine 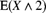 .
. - 14.6 (*) A sample of size 2,000 contains 1,700 observations that are no greater than 6,000, 30 that are greater than 6,000 but no greater than 7,000, and 270 that are greater than 7,000. The total amount of the 30 observations that are between 6,000 and 7,000 is 200,000. The value of
 for the empirical distribution associated with these observations is 1,810. Determine
for the empirical distribution associated with these observations is 1,810. Determine  for the empirical distribution.
for the empirical distribution. - 14.7 (*) A random sample of unknown size produced 36 observations between 0 and 50; x between 50 and 150; y between 150 and 250; 84 between 250 and 500; 80 between 500 and 1,000; and none above 1,000. Two values of the ogive constructed from these observations are
 and
and 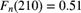 . Determine the value of x.
. Determine the value of x. - 14.8 The data in Table 14.7 are from Hogg and Klugman [55, p. 128]. They represent the total damage done by 35 hurricanes between the years 1949 and 1980. The losses have been adjusted for inflation (using the Residential Construction Index) to be in 1981 dollars. The entries represent all hurricanes for which the trended loss was in excess of 5,000,000.
The federal government is considering funding a program that would provide 100% payment for all damages for any hurricane causing damage in excess of 5,000,000. You have been asked to make some preliminary estimates.
- Estimate the mean, standard deviation, coefficient of variation, and skewness for the population of hurricane losses.
- Estimate the first and second limited moments at 500,000,000.
Table 14.7 Trended hurricane losses.
Year Loss (103) Year Loss (103) Year Loss (103) 1964 6,766 1964 40,596 1975 192,013 1968 7,123 1949 41,409 1972 198,446 1971 10,562 1959 47,905 1964 227,338 1956 14,474 1950 49,397 1960 329,511 1961 15,351 1954 52,600 1961 361,200 1966 16,983 1973 59,917 1969 421,680 1955 18,383 1980 63,123 1954 513,586 1958 19,030 1964 77,809 1954 545,778 1974 25,304 1955 102,942 1970 750,389 1959 29,112 1967 103,217 1979 863,881 1971 30,146 1957 123,680 1965 1,638,000 1976 33,727 1979 140,136 - 14.9 (*) There have been 30 claims recorded in a random sampling of claims. There were 2 claims for 2,000, 6 for 4,000, 12 for 6,000, and 10 for 8,000. Determine the empirical skewness coefficient.
14.3 Empirical Estimation with Right Censored Data
In this section, we generalize the empirical approach of the previous section to situations in which the data are not complete. In particular, we assume that individual observations may be right censored. We have the following definition.
In insurance claims data, the presence of a policy limit may give rise to right censored observations. When the amount of the loss equals or exceeds the limit u, benefits beyond that value are not paid, and so the exact value is typically not recorded. However, it is known that a loss of at least u has occurred.
When carrying out a study of the mortality of humans, if a person is alive when the study ends, right censoring has occurred. The person's age at death is not known, but it is known that it is at least as large as the age when the study ended. Right censoring also affects those who exit the study prior to its end due to surrender or lapse. Note that this discussion could have been about other decrements, such as disability, policy surrender, or retirement.
For this section and the next two, we assume that the underlying random variable has a continuous distribution. While data from discrete random variables can also be right censored (Data Set A is an example), the use of empirical estimators is rare and thus the development of analogous formulas is unlikely to be worth the effort.
We now make specific assumptions regarding how the data are collected and recorded. It is assumed that we have a random sample for which some (but not all) of the data are right censored. For the uncensored (i.e. completely known) observations, we will denote their k unique values by ![]() . We let
. We let ![]() denote the number of times that
denote the number of times that ![]() appears in the sample. We also set
appears in the sample. We also set ![]() as the minimum possible value for an observation and assume that
as the minimum possible value for an observation and assume that ![]() . Often,
. Often, ![]() . Similarly, set
. Similarly, set ![]() as the largest observation in the data, censored or uncensored. Hence,
as the largest observation in the data, censored or uncensored. Hence, ![]() . Our goal is to create an empirical (data-dependent) distribution that places probability at the values
. Our goal is to create an empirical (data-dependent) distribution that places probability at the values ![]() .
.
We often possess the specific value at which an observation was censored. However, for both the derivation of the estimator and its implementation, it is only necessary to know between which y-values it occurred. Thus, the only input needed is ![]() , the number of right censored observations in the interval
, the number of right censored observations in the interval ![]() for
for ![]() . We make the assumption that if an observation is censored at
. We make the assumption that if an observation is censored at ![]() , then the observation is censored at
, then the observation is censored at ![]() (i.e. in the lifetime situation, immediately after the death). It is possible to have censored observations at values between
(i.e. in the lifetime situation, immediately after the death). It is possible to have censored observations at values between ![]() and
and ![]() . However, because we are placing probability only at the uncensored values, these observations provide no information about those probabilities and so can be dropped. When referring to the sample size, n will denote the number of observations after these have been dropped. Observations censored at
. However, because we are placing probability only at the uncensored values, these observations provide no information about those probabilities and so can be dropped. When referring to the sample size, n will denote the number of observations after these have been dropped. Observations censored at ![]() or above cannot be ignored. Let
or above cannot be ignored. Let ![]() be the number of observations right censored at
be the number of observations right censored at ![]() or later. Note that if
or later. Note that if ![]() , then
, then ![]() .
.
The final important quantity is ![]() , referred to as the number “at risk” at
, referred to as the number “at risk” at ![]() . When thinking in terms of a mortality study, the risk set comprises the individuals who are under observation at that age. Included are all who die at that age or later and all who are censored at that age or later. Formally, we have the following definition.
. When thinking in terms of a mortality study, the risk set comprises the individuals who are under observation at that age. Included are all who die at that age or later and all who are censored at that age or later. Formally, we have the following definition.
This formula reflects the fact that the number at risk at ![]() is that at
is that at ![]() less the
less the ![]() exact observations at
exact observations at ![]() and the
and the ![]() censored observations in
censored observations in ![]() . Note that
. Note that ![]() and hence
and hence ![]() .
.
The following numerical example illustrates these ideas.
![]()
It should be noted that if there is no censoring, so that ![]() for all i, then the data are complete and the techniques of Section 14.1 may be used. As such, the approach of this section may be viewed as a generalization.
for all i, then the data are complete and the techniques of Section 14.1 may be used. As such, the approach of this section may be viewed as a generalization.
We shall now present a heuristic derivation of a well-known generalization of the empirical distribution function. This estimator is referred to as either the Kaplan–Meier or the product limit estimator.
To proceed, we first present some basic facts regarding the distribution of a discrete random variable Y, say, with support on the points ![]() . Let
. Let ![]() , and then the survival function is (where
, and then the survival function is (where ![]() means to take the sum or product over all values of i where
means to take the sum or product over all values of i where ![]() )
)
Setting ![]() for
for ![]() , we have
, we have

and ![]() . We also have
. We also have ![]() from the definition of
from the definition of ![]() .
.
Thus,
implying that ![]() . Hence,
. Hence,
Also, ![]() , and for
, and for ![]() ,
,
The heuristic derivation proceeds by viewing ![]() for
for ![]() as unknown parameters, and estimating them by a nonparametric “maximum likelihood” bsed argument.3 For a more detailed discussion, see Lawless [77]. For the present data, the
as unknown parameters, and estimating them by a nonparametric “maximum likelihood” bsed argument.3 For a more detailed discussion, see Lawless [77]. For the present data, the ![]() uncensored observations at
uncensored observations at ![]() each contribute
each contribute ![]() to the likelihood where
to the likelihood where ![]() and
and
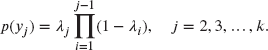
Each of the ![]() censored observations contributes
censored observations contributes
to the likelihood (recall that ![]() for
for ![]() ), and the
), and the ![]() censored observations at or above
censored observations at or above ![]() each contribute
each contribute ![]() .
.
The likelihood is formed by taking products over all contributions (assuming independence of all data points), namely

which, in terms of the ![]() , becomes
, becomes

where the last line follows by interchanging the order of multiplication in each of the two double products. Thus,
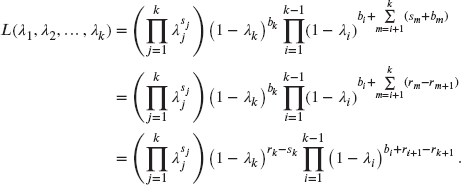
Observe that ![]() and
and ![]() . Hence,
. Hence,

This likelihood has the appearance of a product of binomial likelihoods. That is, this is the same likelihood as if ![]() were realizations of k independent binomial observations with parameters
were realizations of k independent binomial observations with parameters ![]() and
and ![]() . The “maximum likelihood estimate”
. The “maximum likelihood estimate” ![]() of
of ![]() is obtained by taking logarithms, namely
is obtained by taking logarithms, namely

implying that
Equating this latter expression to zero yields ![]() .
.
For ![]() , the Kaplan–Meier [66] estimate
, the Kaplan–Meier [66] estimate ![]() of
of ![]() is obtained by replacing
is obtained by replacing ![]() by
by ![]() wherever it appears. Noting that
wherever it appears. Noting that ![]() for
for ![]() , it follows that
, it follows that

This may be written more succinctly as ![]() for
for ![]() . When
. When ![]() , you should interpret
, you should interpret ![]() as
as ![]() .
.
![]()
We now discuss estimation for ![]() . First, note that if
. First, note that if ![]() (no censored observations at
(no censored observations at ![]() ), then
), then ![]() and
and ![]() for
for ![]() is clearly the (only) obvious choice. However, if
is clearly the (only) obvious choice. However, if ![]() , as in the previous example, there are no empirical data to estimate
, as in the previous example, there are no empirical data to estimate ![]() for
for ![]() , and tail estimates for
, and tail estimates for ![]() (often called tail corrections) are needed. There are three popular extrapolations:
(often called tail corrections) are needed. There are three popular extrapolations:
- Efron's tail correction [31] assumes that
 for
for  .
. - Klein and Moeschberger [70, p. 118] assume that
 for
for  and
and  for
for  , where
, where  is a plausible upper limit for the underlying random variable. For example, in a study of human mortality, the limit might be 120 years.
is a plausible upper limit for the underlying random variable. For example, in a study of human mortality, the limit might be 120 years. - Brown, Hollander, and Korwar's exponential tail correction [18] assumes that
 and that
and that  for
for  . With
. With  ,
,  , and thus
, and thus

![]()
Note that if there is no censoring (![]() for all i), then
for all i), then ![]() , and for
, and for ![]()
In this case, ![]() is the number of observations exceeding y and
is the number of observations exceeding y and ![]() . Thus, with no censoring, the Kaplan–Meier estimate reduces to the empirical estimate of the previous section.
. Thus, with no censoring, the Kaplan–Meier estimate reduces to the empirical estimate of the previous section.
An alternative to the Kaplan–Meier estimator, called the Nelson–Åalen estimator [1], [93], is sometimes used. To motivate the estimator, note that if ![]() is the survival function of a continuous distribution with failure rate
is the survival function of a continuous distribution with failure rate ![]() , then
, then ![]() is called the cumulative hazard rate function. The discrete analog is, in the present context, given by
is called the cumulative hazard rate function. The discrete analog is, in the present context, given by ![]() , which can intuitively be estimated by replacing
, which can intuitively be estimated by replacing ![]() by its estimate
by its estimate ![]() . The Nelson–Åalen estimator of
. The Nelson–Åalen estimator of ![]() is thus defined for
is thus defined for ![]() to be
to be

That is, ![]() for
for ![]() , and the Nelson–Åalen estimator of the survival function is
, and the Nelson–Åalen estimator of the survival function is ![]() . The notation under the summation sign indicates that values of
. The notation under the summation sign indicates that values of ![]() should be included only if
should be included only if ![]() . For
. For ![]() , the situation is similar to that involving the Kaplan–Meier estimate in the sense that a tail correction of the type discussed earlier needs to be employed. Note that, unlike the Kaplan–Meier estimate,
, the situation is similar to that involving the Kaplan–Meier estimate in the sense that a tail correction of the type discussed earlier needs to be employed. Note that, unlike the Kaplan–Meier estimate, ![]() , so that a tail correction is always needed.
, so that a tail correction is always needed.
![]()
To assess the quality of the two estimators, we will now consider estimation of the variance. Recall that for ![]() , the Kaplan–Meier estimator may be expressed as
, the Kaplan–Meier estimator may be expressed as
which is a function of the ![]() . Thus, to estimate the variance of
. Thus, to estimate the variance of ![]() , we first need the covariance matrix of
, we first need the covariance matrix of ![]() . We estimate this from the “likelihood,” using standard likelihood methods. Recall that
. We estimate this from the “likelihood,” using standard likelihood methods. Recall that

and thus ![]() satisfies
satisfies

Thus,
and
which, with ![]() replaced by
replaced by ![]() , becomes
, becomes

For ![]() ,
,
The observed information, evaluated at the maximum likelihood estimate, is thus a diagonal matrix, which when inverted yields the estimates
and
These results also follow directly from the binomial form of the likelihood.
Returning to the problem at hand, the delta method4 gives the approximate variance of ![]() as
as ![]() , for an estimator
, for an estimator ![]() .
.
To proceed, note that
and since the ![]() are assumed to be approximately uncorrelated,
are assumed to be approximately uncorrelated,
The choice ![]() yields
yields
implying that
Because ![]() , the delta method with
, the delta method with ![]() yields
yields
This yields the final version of the estimate,
Equation (14.2) holds for ![]() in all cases. However, if
in all cases. However, if ![]() (that is, there are no censored observations after the last uncensored observation), then it holds for
(that is, there are no censored observations after the last uncensored observation), then it holds for ![]() . Hence the formula always holds for
. Hence the formula always holds for ![]() .
.
Formula (14.2) is known as Greenwood's approximation to the variance of ![]() , and is known to often understate the true variance.
, and is known to often understate the true variance.
If there is no censoring, and we take ![]() , then Greenwood's approximation yields
, then Greenwood's approximation yields
which may be expressed (using ![]() due to no censoring) as
due to no censoring) as

Because ![]() , this sum telescopes to give
, this sum telescopes to give
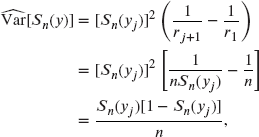
which is the same estimate as obtained in Section 14.1, but derived without use of the delta method.
We remark that in the case with ![]() (i.e.
(i.e. ![]() ), Greenwood's approximation cannot be used to estimate the variance of
), Greenwood's approximation cannot be used to estimate the variance of ![]() . In this case,
. In this case, ![]() is often replaced by
is often replaced by ![]() in the denominator.
in the denominator.
Turning now to the Nelson–Åalen estimator, we note that
and the same reasoning used for Kaplan–Meier implies that ![]() , yielding the estimate
, yielding the estimate
which is referred to as Klein's estimate. A commonly used alternative estimate due to Åalen is obtained by replacing ![]() with
with ![]() in the numerator.
in the numerator.
We are typically more interested in ![]() than
than ![]() . Because
. Because ![]() , the delta method with
, the delta method with ![]() yields Klein's survival function estimate
yields Klein's survival function estimate
that is, the estimated variance is
![]()
Variance estimates for ![]() depend on the tail correction used. Efron's method gives an estimate of 0, which is not of interest in the present context. For the exponential tail correction in the Kaplan–Meier case, we have for
depend on the tail correction used. Efron's method gives an estimate of 0, which is not of interest in the present context. For the exponential tail correction in the Kaplan–Meier case, we have for ![]() ,
, ![]() , and the delta method with
, and the delta method with ![]() yields
yields

Likelihood methods typically result in approximate asymptotic normality of the estimates, and this is true for Kaplan–Meier and Nelson–Åalen estimates as well. Using the results of Example 14.9, an approximate 95% confidence interval for ![]() is given by
is given by
For ![]() , the Nelson–Åalen estimate gives a confidence interval of
, the Nelson–Åalen estimate gives a confidence interval of
whereas that based on the Kaplan–Meier estimate is
Clearly, both confidence intervals for ![]() are unsatisfactory, both including values greater than 1.
are unsatisfactory, both including values greater than 1.
An alternative approach can be constructed as follows, using the Kaplan–Meier estimate as an example.
Let ![]() . Using the delta method, the variance of Y can be approximated as follows. The function of interest is
. Using the delta method, the variance of Y can be approximated as follows. The function of interest is ![]() . Its derivative is
. Its derivative is
According to the delta method,
Then, an approximate 95% confidence interval for ![]() is
is

Because ![]() , evaluating each endpoint of this formula provides a confidence interval for
, evaluating each endpoint of this formula provides a confidence interval for ![]() . For the upper limit, we have (where
. For the upper limit, we have (where ![]() )
)

Similarly, the lower limit is ![]() . This interval will always be inside the range 0–1 and is referred to as a log-transformed confidence interval.
. This interval will always be inside the range 0–1 and is referred to as a log-transformed confidence interval.
![]()
For the Nelson–Åalen estimator, a similar log-transformed confidence interval for ![]() has endpoints
has endpoints ![]() , where
, where ![]() . Exponentiation of the negative of these endpoints yields a corresponding interval for
. Exponentiation of the negative of these endpoints yields a corresponding interval for ![]() .
.
![]()
14.3.1 Exercises
- 14.10 (*) You are given the following times of first claim for five randomly selected automobile insurance policies: 1, 2, 3, 4, and 5. You are later told that one of the five times given is actually the time of policy lapse, but you are not told which one. The smallest product-limit estimate of
 , the probability that the first claim occurs after time 4, would result if which of the given times arose from the lapsed policy?
, the probability that the first claim occurs after time 4, would result if which of the given times arose from the lapsed policy? - 14.11 (*) For a mortality study with right censored data, you are given the information in Table 14.12. Calculate the estimate of the survival function at time 12 using the Nelson–Åalen estimate.
Table 14.12 The data for Exercise 14.11.
Time Number of deaths Number at risk 


5 2 15 7 1 12 10 1 10 12 2 6 - 14.12 (*) Let n be the number of lives observed from birth. None were censored and no two lives died at the same age. At the time of the ninth death, the Nelson–Åalen estimate of the cumulative hazard rate is 0.511, and at the time of the tenth death it is 0.588. Estimate the value of the survival function at the time of the third death.
- 14.13 (*) All members of a study joined at birth; however, some may exit the study by means other than death. At the time of the third death, there was one death (i.e.
 ); at the time of the fourth death, there were two deaths; and at the time of the fifth death, there was one death. The following product-limit estimates were obtained:
); at the time of the fourth death, there were two deaths; and at the time of the fifth death, there was one death. The following product-limit estimates were obtained:  ,
,  , and
, and  . Determine the number of censored observations between times
. Determine the number of censored observations between times  and
and  . Assume that no observations were censored at the death times.
. Assume that no observations were censored at the death times. - 14.14 (*) A mortality study has right censored data and no left truncated data. Uncensored observations occurred at ages 3, 5, 6, and 10. The risk sets at these ages were 50, 49, k, and 21, respectively, while the number of deaths observed at these ages were 1, 3, 5, and 7, respectively. The Nelson–Åalen estimate of the survival function at time 10 is 0.575. Determine k.
- 14.15 (*) Consider the observations 2,500, 2,500, 2,500, 3,617, 3,662, 4,517, 5,000, 5,000, 6,010, 6,932, 7,500, and 7,500. No truncation is possible. First, determine the Nelson–Åalen estimate of the cumulative hazard rate function at 7,000, assuming that all the observations are uncensored. Second, determine the same estimate, assuming that the observations at 2,500, 5,000, and 7,500 were right censored.
- 14.16 (*) No observations in a data set are truncated. Some are right censored. You are given
 ,
,  , and the Kaplan–Meier estimates
, and the Kaplan–Meier estimates  ,
,  , and
, and  . Also, between the observations
. Also, between the observations  and
and  there are six right censored observations and no observations were right censored at the same value as an uncensored observation. Determine
there are six right censored observations and no observations were right censored at the same value as an uncensored observation. Determine  .
. - 14.17 For Data Set A, determine the empirical estimate of the probability of having two or more accidents and estimate its variance.
- 14.18 (*) Ten individuals were observed from birth. All were observed until death. Table 14.13 gives the death ages. Let
 denote the estimated conditional variance of
denote the estimated conditional variance of  if calculated without any distribution assumption. Let
if calculated without any distribution assumption. Let  denote the conditional variance of
denote the conditional variance of  if calculated knowing that the survival function is
if calculated knowing that the survival function is  . Determine
. Determine  .
.
Table 14.13 The data for Exercise 14.18.
Age Number of deaths 2 1 3 1 5 1 7 2 10 1 12 2 13 1 14 1 - 14.19 (*) Observations can be censored, but there is no truncation. Let
 and
and  be consecutive death ages. A 95% linear confidence interval for
be consecutive death ages. A 95% linear confidence interval for  using the Klein estimator is
using the Klein estimator is  , while a similar interval for
, while a similar interval for  is
is  . Determine
. Determine  .
. - 14.20 (*) A mortality study is conducted on 50 lives, all observed from age 0. At age 15 there were two deaths; at age 17 there were three censored observations; at age 25 there were four deaths; at age 30 there were c censored observations; at age 32 there were eight deaths; and at age 40 there were two deaths. Let S be the product-limit estimate of
 and let V be the Greenwood approximation of this estimator's variance. You are given
and let V be the Greenwood approximation of this estimator's variance. You are given  . Determine the value of c.
. Determine the value of c. - 14.21 (*) Fifteen cancer patients were observed from the time of diagnosis until the earlier of death or 36 months from diagnosis. Deaths occurred as follows: at 15 months there were two deaths; at 20 months there were three deaths; at 24 months there were two deaths; at 30 months there were d deaths; at 34 months there were two deaths; and at 36 months there was one death. The Nelson–Åalen estimate of
 is 1.5641. Determine Klein's estimate of the variance of this estimator.
is 1.5641. Determine Klein's estimate of the variance of this estimator. - 14.22 (*) Ten payments were recorded as follows: 4, 4, 5, 5, 5, 8, 10, 10, 12, and 15, with the italicized values representing payments at a policy limit. There were no deductibles. Determine the product-limit estimate of
 and Greenwood's approximation of its variance.
and Greenwood's approximation of its variance. - 14.23 (*) All observations begin on day 0. Eight observations were 4, 8, 8, 12, 12, 12, 22, and 36, with the italicized values representing right censored observations. Determine the Nelson–Åalen estimate of
 and then determine a 90% linear confidence interval for the true value using Klein's variance estimate.
and then determine a 90% linear confidence interval for the true value using Klein's variance estimate. - 14.24 You are given the data in Table 14.14, based on 40 observations. Dashes indicate missing observations that must be deduced.
- Compute the Kaplan–Meier estimate
 for
for  .
. - Compute the Nelson–Åalen estimate
 for
for  .
. - Compute
 using the method of Brown, Hollander, and Korwar.
using the method of Brown, Hollander, and Korwar. - Compute Greenwood's approximation,
 .
. - Compute a 95% linear confidence interval for
 using the Kaplan–Meier estimate.
using the Kaplan–Meier estimate. - Compute a 95% log-transformed confidence interval for
 using the Kaplan–Meier estimate.
using the Kaplan–Meier estimate.
Table 14.14 The data for Exercise 14.24.
i 



1 4 3 — 40 2 6 — 3 31 3 9 6 4 23 4 13 4 — — 5 15 2 4 6 - Compute the Kaplan–Meier estimate
- 14.25 You are given the data in Table 14.15, based on 50 observations.
- Compute the Kaplan–Meier estimate
 for
for  .
. - Compute the Nelson–Åalen estimate
 for
for  .
. - Compute
 using Efron's tail correction, and also using the exponential tail correction of Brown, Hollander, and Korwar.
using Efron's tail correction, and also using the exponential tail correction of Brown, Hollander, and Korwar. - Compute Klein's survival function estimate of the variance of
 .
. - Compute a 95% log-transformed confidence interval for
 based on the Nelson–Åalen estimate.
based on the Nelson–Åalen estimate. - Using the exponential tail correction method of Brown, Hollander, and Korwar, estimate the variance of
 .
.
Table 14.15 The data for Exercise 14.25.
i 



1 3 3 6 50 2 5 7 4 41 3 7 5 2 30 4 11 5 3 23 5 16 6 4 15 6 20 2 3 5 - Compute the Kaplan–Meier estimate
- 14.26 Consider the estimator

where
 is differentiable.
is differentiable.- Show that
 becomes the Kaplan–Meier estimator
becomes the Kaplan–Meier estimator  when
when  , and
, and  becomes the Nelson–Åalen estimator
becomes the Nelson–Åalen estimator  when
when  .
. - Derive the variance estimate

- Consider

Prove that
 if
if 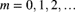 , and
, and  if
if  , and thus that
, and thus that  in particular.
in particular.Hint: Prove by induction on m the identity
 for
for  and
and  .
.
- Show that
14.4 Empirical Estimation of Moments
In the previous section, we focused on estimation of the survival function ![]() or, equivalently, the cumulative distribution function
or, equivalently, the cumulative distribution function ![]() , of a random variable Y. In many actuarial applications, other quantities such as raw moments are of interest. Of central importance in this context is the mean, particularly for premium calculation in a loss modelling context.
, of a random variable Y. In many actuarial applications, other quantities such as raw moments are of interest. Of central importance in this context is the mean, particularly for premium calculation in a loss modelling context.
For estimation of the mean with complete data ![]() , an obvious (unbiased) estimation is
, an obvious (unbiased) estimation is ![]() , but for incomplete data such as that of the previous section involving right censoring, other methods are needed. We continue to assume that we have the setting described in the previous section, and we will capitalize on the results obtained for
, but for incomplete data such as that of the previous section involving right censoring, other methods are needed. We continue to assume that we have the setting described in the previous section, and we will capitalize on the results obtained for ![]() there. To do so, we recall that, for random variables that take on only nonnegative values, the mean satisfies
there. To do so, we recall that, for random variables that take on only nonnegative values, the mean satisfies
and empirical estimation of ![]() may be done by replacing
may be done by replacing ![]() with an estimator such as the Kaplan–Meier estimator
with an estimator such as the Kaplan–Meier estimator ![]() or the Nelson–Åalen estimator
or the Nelson–Åalen estimator ![]() . To unify the approach, we will assume that
. To unify the approach, we will assume that ![]() is estimated for
is estimated for ![]() by the estimator given in Exercise 14.26 of Section 14.3, namely
by the estimator given in Exercise 14.26 of Section 14.3, namely
where ![]() for the Kaplan–Meier estimator and
for the Kaplan–Meier estimator and ![]() for the Nelson–Åalen estimator. The mean is obtained by replacing
for the Nelson–Åalen estimator. The mean is obtained by replacing ![]() with
with ![]() in the integrand. This yields the estimator
in the integrand. This yields the estimator
It is convenient to write
where
and
Anticipating what follows, we wish to evaluate ![]() for
for ![]() . For
. For ![]() , we have that
, we have that ![]() for
for ![]() . Thus
. Thus
To evaluate ![]() for
for ![]() , recall that
, recall that ![]() for
for ![]() and for
and for ![]() ,
, ![]() . Thus,
. Thus,
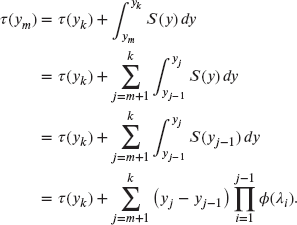
For evaluation of ![]() , note that
, note that
and also that for ![]() ,
,
a recursive formula, beginning with ![]() .
.
For the estimates themselves, ![]() , and the above formulas continue to hold when
, and the above formulas continue to hold when ![]() is replaced by
is replaced by ![]() ,
, ![]() by
by ![]() , and
, and ![]() by
by ![]() .
.
The estimate of the mean ![]() clearly depends on
clearly depends on ![]() , which in turn depends on the tail correction, that is, on
, which in turn depends on the tail correction, that is, on ![]() for
for ![]() . If
. If ![]() for
for ![]() (as, for example, under Efron's tail correction), then
(as, for example, under Efron's tail correction), then ![]() . Under Klein and Moeschberger's method, with
. Under Klein and Moeschberger's method, with ![]() for
for ![]() , and
, and ![]() for
for ![]() where
where ![]() ,
,
For the exponential tail correction of Brown, Hollander, and Korwar, ![]() for
for ![]() with
with ![]() . Thus
. Thus
The following example illustrates the calculation of ![]() , where all empirical quantities are obtained by substitution of estimates.
, where all empirical quantities are obtained by substitution of estimates.
![]()
To estimate the variance of ![]() , we note that
, we note that ![]() is a function of
is a function of ![]() , for which we have an estimate of the variance matrix from the previous section. In particular,
, for which we have an estimate of the variance matrix from the previous section. In particular, ![]() is a
is a ![]() diagonal matrix (i.e. all off-diagonal elements are 0). Thus, by the multivariate delta method, with the
diagonal matrix (i.e. all off-diagonal elements are 0). Thus, by the multivariate delta method, with the ![]() matrix A with jth entry
matrix A with jth entry ![]() , the estimated variance of
, the estimated variance of ![]() is
is

and it remains to identify ![]() for
for ![]() .
.
To begin, first note that ![]() depends on
depends on ![]() , which in turn depends on
, which in turn depends on ![]() but also on the tail correction employed. As such, we will express the formulas in terms of
but also on the tail correction employed. As such, we will express the formulas in terms of ![]() for
for ![]() for the moment. We first consider
for the moment. We first consider ![]() for
for ![]() . Then,
. Then,

In the above expression, ![]() does not appear in the first
does not appear in the first ![]() terms of the summation, that is, for
terms of the summation, that is, for ![]() . Thus,
. Thus,
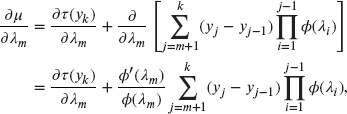
and in terms of ![]() , this may be expressed as
, this may be expressed as
It is also useful to note that ![]() does not involve
does not involve ![]() and thus
and thus ![]() . The general variance formula thus may be written as
. The general variance formula thus may be written as

But

and thus,
in turn implying that
The variance is estimated by replacing parameters with their estimates in the above formula. This yields

where we understand ![]() to mean
to mean ![]() with
with ![]() replaced by
replaced by ![]() and
and ![]() by
by ![]() .
.
If ![]() , then
, then

a formula that further simplifies, under the Kaplan–Meier assumption ![]() (recalling that
(recalling that ![]() ), to
), to
We note that ![]() if no tail correction is necessary, because
if no tail correction is necessary, because ![]() (in which case
(in which case ![]() as well and the upper limit of the summation is
as well and the upper limit of the summation is ![]() ), or under Efron's approximation.
), or under Efron's approximation.
For Klein and Moeschberger's method,
implying that
resulting in the same variance formula as under Efron's method [but ![]() is increased by
is increased by ![]() for this latter approximation].
for this latter approximation].
Turning now to the exponential tail correction with ![]() , recall that
, recall that ![]() and
and ![]() . Thus
. Thus

Therefore, under the exponential tail correction, the general variance estimate becomes

In the Nelson–Åalen case with ![]() , the term
, the term ![]() may obviously be omitted.
may obviously be omitted.
![]()
For higher moments, a similar approach may be used. We have, for the ![]() th moment,
th moment,
which may be estimated (using ![]() without loss of generality) by
without loss of generality) by

Again, the final integral on the right-hand side depends on the tail correction, and is 0 if ![]() or under Efron's tail correction. It is useful to note that under the exponential tail correction,
or under Efron's tail correction. It is useful to note that under the exponential tail correction, ![]() for
for ![]() with
with ![]() , and if
, and if ![]() ,
,

using the tail function representation of the gamma distribution. That is, under the exponential tail correction,

In particular, for the second moment ![]() ,
,
Variance estimation for ![]() may be done in a similar manner as for the mean, if desired.
may be done in a similar manner as for the mean, if desired.
14.4.1 Exercises
- 14.27 For the data of Exercise 14.24 and using the Kaplan–Meier estimate:
- Compute the mean survival time estimate assuming Efron's tail correction.
- Compute the mean survival time estimate using the exponential tail correction of Brown, Hollander, and Korwar.
- Estimate the variance of the estimate in (a).
- 14.28 For the data of Exercise 14.25, using the Nelson–Åalen estimate and the exponential tail correction of Brown, Hollander, and Korwar:
- Estimate the mean
 .
. - Estimate the variance of
 in (b).
in (b).
- Estimate the mean
- 14.29 For the data in Example 14.5 and subsequent examples, using the Nelson–Åalen estimate with the exponential tail correction of Brown, Hollander, and Korwar, estimate the variance of Y.
14.5 Empirical Estimation with Left Truncated Data
The results of Section 14.3 apply in situations in which the data are (right) censored. In this section, we discuss the situation in which the data may also be (left) truncated. We have the following definitions.
In insurance survival data and claim data, the most common occurrences are left truncation and right censoring. Left truncation occurs when an ordinary deductible of d is applied. When a policyholder has a loss below d, he or she realizes no benefits will be paid and so does not inform the insurer. When the loss is above d, the amount of the loss is assumed to be reported.5 A policy limit leads to an example of right censoring. When the amount of the loss equals or exceeds u, benefits beyond that value are not paid, and so the exact value is not recorded. However, it is known that a loss of at least u has occurred.
For decrement studies, such as of human mortality, it is impractical to follow people from birth to death. It is more common to follow a group of people of varying ages for a few years during the study period. When a person joins a study, he or she is alive at that time. This person's age at death must be at least as great as the age at entry to the study and thus has been left truncated. If the person is alive when the study ends, right censoring has occurred. The person's age at death is not known, but it is known that it is at least as large as the age when the study ended. Right censoring also affects those who exit the study prior to its end due to surrender. Note that this discussion could have been about other decrements, such as disability, policy surrender, or retirement.
Because left truncation and right censoring are the most common occurrences in actuarial work, they are the only cases that are covered in this section. To save words, truncated always means truncated from below and censored always means censored from above.
When trying to construct an empirical distribution from truncated or censored data, the first task is to create notation to represent the data. For individual (as opposed to grouped) data, the following facts are needed. The first is the truncation point for that observation. Let that value be ![]() for the jth observation. If there was no truncation,
for the jth observation. If there was no truncation, ![]() .6 Next, record the observation itself. The notation used depends on whether or not that observation was censored. If it was not censored, let its value be
.6 Next, record the observation itself. The notation used depends on whether or not that observation was censored. If it was not censored, let its value be ![]() . If it was censored, let its value be
. If it was censored, let its value be ![]() . When this subject is presented more formally, a distinction is made between the case where the censoring point is known in advance and where it is not. For example, a liability insurance policy with a policy limit usually has a censoring point that is known prior to the receipt of any claims. By comparison, in a mortality study of insured lives, those that surrender their policy do so at an age that was not known when the policy was sold. In this chapter, no distinction is made between the two cases.
. When this subject is presented more formally, a distinction is made between the case where the censoring point is known in advance and where it is not. For example, a liability insurance policy with a policy limit usually has a censoring point that is known prior to the receipt of any claims. By comparison, in a mortality study of insured lives, those that surrender their policy do so at an age that was not known when the policy was sold. In this chapter, no distinction is made between the two cases.
To construct the estimate, the raw data must be summarized in a useful manner. The most interesting values are the uncensored observations. As in Section 14.3, let ![]() be the k unique values of the
be the k unique values of the ![]() that appear in the sample, where k must be less than or equal to the number of uncensored observations. We also continue to let
that appear in the sample, where k must be less than or equal to the number of uncensored observations. We also continue to let ![]() be the number of times the uncensored observation
be the number of times the uncensored observation ![]() appears in the sample. Again, an important quantity is
appears in the sample. Again, an important quantity is ![]() , the number “at risk” at
, the number “at risk” at ![]() . In a decrement study,
. In a decrement study, ![]() represents the number under observation and subject to the decrement at that time. To be under observation at
represents the number under observation and subject to the decrement at that time. To be under observation at ![]() , an individual must (1) either be censored or have an observation that is on or after
, an individual must (1) either be censored or have an observation that is on or after ![]() and (2) not have a truncation value that is on or after
and (2) not have a truncation value that is on or after ![]() . That is,
. That is,
Alternatively, because the total number of ![]() is equal to the total number of
is equal to the total number of ![]() and
and ![]() , we also have
, we also have
This latter version is a bit easier to conceptualize because it includes all who have entered the study prior to the given age less those who have already left. The key point is that the number at risk is the number of people observed alive at age ![]() . If the data are loss amounts, the risk set is the number of policies with observed loss amounts (either the actual amount or the maximum amount due to a policy limit) greater than or equal to
. If the data are loss amounts, the risk set is the number of policies with observed loss amounts (either the actual amount or the maximum amount due to a policy limit) greater than or equal to ![]() less those with deductibles greater than or equal to
less those with deductibles greater than or equal to ![]() . These relationships lead to a recursive version of the formula,
. These relationships lead to a recursive version of the formula,
where between is interpreted to mean greater than or equal to ![]() and less than
and less than ![]() , and
, and ![]() is set equal to zero.
is set equal to zero.
A consequence of the above definitions is that if a censoring or truncation time equals that of a death, the death is assumed to have happened first. That is, the censored observation is considered to be at risk while the truncated observation is not.
The definition of ![]() presented here is consistent with that in Section 14.3. That is, if
presented here is consistent with that in Section 14.3. That is, if ![]() for all observations, the formulas presented here reduce match those presented earlier. The following example illustrates calculating the number at risk when there is truncation.
for all observations, the formulas presented here reduce match those presented earlier. The following example illustrates calculating the number at risk when there is truncation.
![]()
The approach to developing an empirical estimator of the survival function is to use the formulas developed in Section 14.3, but with this more general definition of ![]() . A theoretical treatment that incorporates left truncation is considerably more complex (for details, see Lawless [77]).
. A theoretical treatment that incorporates left truncation is considerably more complex (for details, see Lawless [77]).
The formula for the Kaplan–Meier estimate is the same as presented earlier, namely

The same tail corrections developed in Section 14.3 can be used for ![]() in cases where
in cases where ![]() .
.
![]()
In this example, a tail correction is not needed because an estimate of survival beyond the five-year term is of no value when analyzing these policyholders.
The same analogy holds for the Nelson–Åalen estimator, where the formula for the cumulative hazard function remains

As before, ![]() for
for ![]() and for
and for ![]() the same tail corrections can be used.
the same tail corrections can be used.
![]()
In this section, the results were not formally developed, as was done for the case with only right censored data. However, all the results, including formulas for moment estimates and estimates of the variance of the estimators, hold when left truncation is added. However, it is important to note that when the data are truncated, the resulting distribution function is the distribution function of observations given that they are above the smallest truncation point (i.e. the smallest d value). Empirically, there is no information about observations below that value, and thus there can be no information for that range. Finally, if it turns out that there was no censoring or truncation, use of the formulas in this section will lead to the same results as when using the empirical formulas in Section 14.1.
14.5.1 Exercises
- 14.30 Repeat Example 14.14, treating “surrender” as “death.” The easiest way to do this is to reverse the x and u labels. In this case, death produces censoring because those who die are lost to observation and thus their surrender time is never observed. Treat those who lasted the entire five years as surrenders at that time.
- 14.31 Determine the Kaplan–Meier estimate for the time to surrender for Data Set D. Treat those who lasted the entire five years as surrenders at that time.
- 14.32 Determine the Nelson–Åalen estimate of
 and
and  for Data Set D, where the variable is time to surrender.
for Data Set D, where the variable is time to surrender. - 14.33 Determine the Kaplan–Meier and Nelson–Åalen estimates of the distribution function of the amount of a workers compensation loss. First use the raw data from Data Set B. Then repeat the exercise, modifying the data by left truncation at 100 and right censoring at 1,000.
- 14.34 (*) Three hundred mice were observed at birth. An additional 20 mice were first observed at age 2 (days) and 30 more were first observed at age 4. There were 6 deaths at age 1, 10 at age 3, 10 at age 4, a at age 5, b at age 9, and 6 at age 12. In addition, 45 mice were lost to observation at age 7, 35 at age 10, and 15 at age 13. The following product-limit estimates were obtained:
 and
and  . Determine the values of a and b.
. Determine the values of a and b. - 14.35 Construct 95% confidence intervals for
 by both the linear and log-transformed formulas using all 40 observations in Data Set D, with surrender being the variable of interest.
by both the linear and log-transformed formulas using all 40 observations in Data Set D, with surrender being the variable of interest. - 14.36 (*) For the interval from zero to one year, the exposure (r) is 15 and the number of deaths (s) is 3. For the interval from one to two years, the exposure is 80 and the number of deaths is 24. For two to three years, the values are 25 and 5; for three to four years, they are 60 and 6; and for four to five years, they are 10 and 3. Determine Greenwood's approximation to the variance of
 .
. - 14.37 (*) You are given the values in Table 14.18. Determine the standard deviation of the Nelson–Åalen estimator of the cumulative hazard function at time 20.
Table 14.18 The data for Exercise 14.37.



1 100 15 8 65 20 17 40 13 25 31 31
14.6 Kernel Density Models
One problem with empirical distributions is that they are always discrete. If it is known that the true distribution is continuous, the empirical distribution may be viewed as a poor approximation. In this section, a method of obtaining a smooth, empirical-like distribution, called a kernel density distribution, is introduced. We have the following definition.
Note that the empirical distribution is a special type of kernel smoothed distribution in which the random variable assigns probability 1 to the data point. With regard to kernel smoothing, there are several distributions that could be used, three of which are introduced here.
While not necessary, it is customary that the continuous variable have a mean equal to the value of the point it replaces, ensuring that, overall, the kernel estimate has the same mean as the empirical estimate. One way to think about such a model is that it produces the final observed value in two steps. The first step is to draw a value at random from the empirical distribution. The second step is to draw a value at random from a continuous distribution whose mean is equal to the value drawn at the first step. The selected continuous distribution is called the kernel.
For notation, let ![]() be the probability assigned to the value
be the probability assigned to the value ![]()
![]() by the empirical distribution. Let
by the empirical distribution. Let ![]() be a distribution function for a continuous distribution such that its mean is y. Let
be a distribution function for a continuous distribution such that its mean is y. Let ![]() be the corresponding density function.
be the corresponding density function.
The function ![]() is called the kernel. Three kernels are now introduced: uniform, triangular, and gamma.
is called the kernel. Three kernels are now introduced: uniform, triangular, and gamma.
In each case, there is a parameter that relates to the spread of the kernel. In the first two cases, it is the value of ![]() , which is called the bandwidth. In the gamma case, the value of
, which is called the bandwidth. In the gamma case, the value of ![]() controls the spread, with a larger value indicating a smaller spread. There are other kernels that cover the range from zero to infinity.
controls the spread, with a larger value indicating a smaller spread. There are other kernels that cover the range from zero to infinity.
![]()
14.6.1 Exercises
- 14.38 Provide the formula for the Pareto kernel.
- 14.39 Construct a kernel density estimate for the time to surrender for Data Set D. Be aware of the fact that this is a mixed distribution (probability is continuous from 0 to 5 but is discrete at 5).
- 14.40 (*) You are given the data in Table 14.19 on time to death. Using the uniform kernel with a bandwidth of 60, determine
 .
.
Table 14.19 The data for Exercise 14.40.



10 1 20 34 1 19 47 1 18 75 1 17 156 1 16 171 1 15 - 14.41 (*) You are given the following ages at time of death for 10 individuals: 25, 30, 35, 35, 37, 39, 45, 47, 49, and 55. Using a uniform kernel with a bandwidth of
 , determine the kernel density estimate of the probability of survival to age 40.
, determine the kernel density estimate of the probability of survival to age 40. - 14.42 (*) Given the five observations 82, 126, 161, 294, and 384, determine each of the following estimates of
 :
:
- The empirical estimate.
- The kernel density estimate based on a uniform kernel with bandwidth
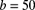 .
. - The kernel density estimate based on a triangular kernel with bandwidth
 .
.
14.7 Approximations for Large Data Sets
14.7.1 Introduction
The discussion in this section is motivated by the circumstances that accompany the determination of a model for the time to death (or other decrement) for use in pricing, reserving, or funding insurance programs. The particular circumstances are as follows:
- Values of the survival function are required only at discrete values, normally integral ages measured in years.
- A large volume of data has been collected over a fixed time period, with most observations truncated, censored, or both.
- No parametric distribution is available that provides an adequate model given the volume of available data.
These circumstances typically apply when an insurance company (or a group of insurance companies) conducts a mortality study based on the historical experience of a very large portfolio of life insurance policies. (For the remainder of this section, we shall refer only to mortality. The results apply equally to the study of other decrements such as disablement or surrender.)
The typical mortality table is essentially a distribution function or a survival function with values presented only at integral ages. While there are parametric models that do well over parts of the age range (such as the Makeham model at ages over about 30), there are too many changes in the pattern from age 0 to ages well over 100 to allow for a simple functional description of the survival function.
The typical mortality study is conducted over a short period of time, such as three to five years. For example, all persons who are covered by an insurance company's policies at some time from January 1, 2014 through December 31, 2016 might be included. Some of these persons may have purchased their policies prior to 2014 and were still covered when the study period started. During the study period some persons will die, some will cancel (surrender) their policy, some will have their policy expire due to policy provisions (such as with term insurance policies that expire during the study period), and some will still be insured when the study ends. It is assumed that if a policy is cancelled or expires, the eventual age at death will not be known to the insurance company. Some persons will purchase their life insurance policy during the study period and be covered for some of the remaining part of the study period. These policies will be subject to the same decrements (death, surrender, expiration) as other policies. With regard to the age at death, almost every policy in the study will be left truncated.8 If the policy was issued prior to 2014, the truncation point will be the age on January 1, 2014. For those who buy insurance during the study period, the truncation point is the age at which the contract begins. For any person who exits the study due to a cause other than death, their observation is right censored at the age of exit, because all that is known about them is that death will be at some unknown later age.
When no simple parametric distribution is appropriate and when large amounts of data are available, it is reasonable to use a nonparametric model because the large amount of data will ensure that key features of the survival function will be captured. Because there are both left truncation (due to the age at entry into the study) and right censoring (due to termination of the study at a fixed time), when there are large amounts of data, constructing the Kaplan–Meier estimate may require a very large amount of sorting and counting. Over the years, a variety of methods have been introduced and entire texts have been written about the problem of constructing mortality tables from this kind of data (e.g. [12, 81]). While the context for the examples presented here is the construction of mortality tables, the methods can apply any time the circumstances described previously apply.
We begin by examining the two ways in which data are usually collected. Estimators will be presented for both situations. The formulas will be presented in this section and their derivation and properties will be provided in Section 14.8. In all cases, a set of values (ages), ![]() has been established in advance and the goal is to estimate the survival function at these values and no others (with some sort of interpolation to be used to provide intermediate values as needed). All of the methods are designed to estimate the conditional one-period probability of death,
has been established in advance and the goal is to estimate the survival function at these values and no others (with some sort of interpolation to be used to provide intermediate values as needed). All of the methods are designed to estimate the conditional one-period probability of death, ![]() , where j may refer to the interval and not to a particular age. From those values,
, where j may refer to the interval and not to a particular age. From those values, ![]() can be evaluated as follows:
can be evaluated as follows:
14.7.2 Using Individual Data Points
In this setting, data are recorded for each person observed. This approach is sometimes referred to as a seriatim method, because the data points are analyzed as a series of individual observations. The estimator takes the form ![]() , where
, where ![]() is the number of observed deaths in the interval and
is the number of observed deaths in the interval and ![]() is a measure of exposure, representing the number of individuals who had a chance to be an observed death in that interval. Should a death occur at one of the boundary values between successive intervals, the death is counted in the preceding interval. When there are no entrants after age
is a measure of exposure, representing the number of individuals who had a chance to be an observed death in that interval. Should a death occur at one of the boundary values between successive intervals, the death is counted in the preceding interval. When there are no entrants after age ![]() into the interval and no exitants except for death during the interval (referred to as complete data),
into the interval and no exitants except for death during the interval (referred to as complete data), ![]() represents the number of persons alive at age
represents the number of persons alive at age ![]() and the number of deaths has a binomial distribution. With incomplete data, it is necessary to determine a suitable convenient approximation, preferably one that requires only a single pass through the data set. To illustrate this challenge, consider the following example.
and the number of deaths has a binomial distribution. With incomplete data, it is necessary to determine a suitable convenient approximation, preferably one that requires only a single pass through the data set. To illustrate this challenge, consider the following example.
![]()
The next step is to tally information for each age interval, building up totals for ![]() and
and ![]() . Counting deaths is straightforward. For exposures, there are two approaches that are commonly used.
. Counting deaths is straightforward. For exposures, there are two approaches that are commonly used.
Exact exposure method
Following this method, we set the exposure equal to the exact total time under observation within the age interval. When a death occurs, that person's exposure ends at the exact age of death. It will be shown in Section 14.8 that ![]() is the maximum likelihood estimator of the hazard rate, under the assumption that the hazard rate is constant over the interval
is the maximum likelihood estimator of the hazard rate, under the assumption that the hazard rate is constant over the interval ![]() . Further properties of this estimator will also be discussed in that section. The estimated hazard rate can then be converted into a conditional probability of death using the formula
. Further properties of this estimator will also be discussed in that section. The estimated hazard rate can then be converted into a conditional probability of death using the formula ![]() .
.
Actuarial exposure method
Under this method, the exposure period for deaths extends to the end of the age interval, rather than the exact age at death. This has the advantage of reproducing the empirical estimator for complete data, but has been shown to be an inconsistent estimator in other cases. In this case, the estimate of the conditional probability of death is obtained as ![]() .
.
When the conditional probability of death is small, with a large number of observations, the choice of method is unlikely to materially affect the results.
![]()
![]()
14.7.2.1 Insuring Ages
While the examples have been in a life insurance context, the methodology applies to any situation with left truncation and right censoring. However, there is a situation that is specific to life insurance studies. Consider a one-year term insurance policy. Suppose that an applicant was born on February 15, 1981 and applies for this insurance on October 15, 2016. Premiums are charged by whole-number ages. Some companies will use the age at the last birthday (35 in this case) and some will use the age at the nearest birthday (36 in this case). One company will base the premium on ![]() and one on
and one on ![]() when both should be using
when both should be using ![]() , the applicant's true age. Suppose that a company uses age last birthday. When estimating
, the applicant's true age. Suppose that a company uses age last birthday. When estimating ![]() , it is not interested in the probability that a person exactly age 35 dies in the next year (the usual interpretation) but, rather, the probability that a random person who is assigned age 35 at issue (who can be anywhere between 35 and 36 years old) dies in the next year. One solution is to obtain a table based on exact ages, assume that the average applicant is 35.5, and use an interpolated value when determining premiums. A second solution is to perform the mortality study using the ages assigned by the company rather than the policyholder's true age. In the example, the applicant is considered to be exactly age 35 on October 15, 2016 and is thus assigned a new birthday of October 15, 1981. When this is done, the study is said to use insuring ages and the resulting values can be used directly for insurance calculations.
, it is not interested in the probability that a person exactly age 35 dies in the next year (the usual interpretation) but, rather, the probability that a random person who is assigned age 35 at issue (who can be anywhere between 35 and 36 years old) dies in the next year. One solution is to obtain a table based on exact ages, assume that the average applicant is 35.5, and use an interpolated value when determining premiums. A second solution is to perform the mortality study using the ages assigned by the company rather than the policyholder's true age. In the example, the applicant is considered to be exactly age 35 on October 15, 2016 and is thus assigned a new birthday of October 15, 1981. When this is done, the study is said to use insuring ages and the resulting values can be used directly for insurance calculations.
![]()
Note that with insuring ages, those who enter observation after the study begins are first observed on their newly assigned birthday. Thus there are no approximation issues with regard to those numbers.
14.7.2.2 Anniversary-Based Mortality Studies
The mortality studies described so far in this section are often called calendar-based or date-to-date studies because the period of study runs from one calendar date to another calendar date. It is also common for mortality studies of insured persons to use a different setup.
Instead of having the observations run from one calendar date to another calendar date, observation for a particular policyholder begins on the first policy anniversary following the fixed start date of the study and ends on the last anniversary prior to the study's fixed end date. Such studies are often called anniversary-to-anniversary studies. We can illustrate this through a previous example.
Consider Example 14.18, with the study now running from anniversaries in 2014 to anniversaries in 2016. The first policy comes under observation on 8-2014 at insuring age 33-0 and exits the study on 8-2016 at insuring age 35-0. Policyholder 2 begins observation on 7-2014 at insuring age 33-0. Policyholder 5 surrendered after the 2016 anniversary, so observation ends on 3-2016 at age 34-0. All other ages remain the same. In this setting, all subjects begin observations at an integral age and all who are active policyholders at the end of the study do so at an integral age. Only the ages of death and surrender may be other than integers (and note that with the actuarial exposure method, in calculating the exposure, deaths are placed at the next integral age). There is a price to be paid for this convenience. In a three-year study such as the one in the example, no single policyholder can be observed for more than two years. In the date-to-date version, some policies will contribute three years of exposure.
All of the examples have used one-year time periods. If the length of an interval ![]() is not equal to 1, an adjustment is necessary. Exposures should be the fraction of the period under observation and not the length of time.
is not equal to 1, an adjustment is necessary. Exposures should be the fraction of the period under observation and not the length of time.
14.7.3 Interval-Based Methods
Instead of recording the exact age at which an event happens, all that is recorded is the age interval in which it took place and the nature of the event. As with the individual method, for a portfolio of insurance policies, only running totals need to be recorded, and the end result is just four to six9 numbers for each age interval:
- The number of persons at the beginning of the interval carried over from the previous interval.
- The number of additional persons entering at the beginning of the interval.
- The number of persons entering during the interval.
- The number of persons exiting by death during the interval.
- The number of persons exiting during the interval for reasons other than death.
- The number of persons exiting at the end of the interval by other than death.
![]()
The analysis of this situation is relatively simple. For the interval from age ![]() to age
to age ![]() , let
, let ![]() be the number of lives under observation at age
be the number of lives under observation at age ![]() . This number includes those carried over from the prior interval as well as those entering at age
. This number includes those carried over from the prior interval as well as those entering at age ![]() . Let
. Let ![]() ,
, ![]() , and
, and ![]() be the number entering, dying, and exiting during the interval. Note that, in general,
be the number entering, dying, and exiting during the interval. Note that, in general, ![]() , as the right-hand side must be adjusted by those who exit or enter at exact age
, as the right-hand side must be adjusted by those who exit or enter at exact age ![]() . Estimating the mortality probability depends on the method selected and an assumption about when the events that occur during the age interval take place.
. Estimating the mortality probability depends on the method selected and an assumption about when the events that occur during the age interval take place.
One approach is to assume a uniform distribution of the events during the interval. For the exact exposure method, the ![]() who start the interval have the potential to contribute a full unit of exposure and the
who start the interval have the potential to contribute a full unit of exposure and the ![]() entrants during the year add another half-year each (on average). Similarly, those who die or exit subtract one-half year on average. Thus the net exposure is
entrants during the year add another half-year each (on average). Similarly, those who die or exit subtract one-half year on average. Thus the net exposure is ![]() . For the actuarial exposure method, those who die do not reduce the exposure, and it becomes
. For the actuarial exposure method, those who die do not reduce the exposure, and it becomes ![]() .
.
Another approach is to adapt the Kaplan–Meier estimator to this situation. Suppose that the deaths all occur at midyear and all other decrements occur uniformly through the year. Then the risk set at midyear is ![]() and the estimator is the same as the actuarial estimator.
and the estimator is the same as the actuarial estimator.
![]()
The goal of all the estimation procedures in this book is to deduce the probability distribution for the random variable in the absence of truncation and censoring. For loss data, that would be the probabilities if there were no deductible or limit, that is, ground-up losses. For lifetime data, it would be the probability distribution of the age at death if we could follow the person from birth to death. These are often referred to as single-decrement probabilities and are typically denoted ![]() in life insurance mathematics. In the life insurance context, the censoring rates are often as important as the mortality rates. For example, in the context of Data Set D, both time to death and time to withdrawal may be of interest. In the former case, withdrawals cause observations to be censored. In the latter case, censoring is caused by death. A superscript identifies the decrement of interest. For example, suppose that the decrements were death (d) and withdrawal (w). Then
in life insurance mathematics. In the life insurance context, the censoring rates are often as important as the mortality rates. For example, in the context of Data Set D, both time to death and time to withdrawal may be of interest. In the former case, withdrawals cause observations to be censored. In the latter case, censoring is caused by death. A superscript identifies the decrement of interest. For example, suppose that the decrements were death (d) and withdrawal (w). Then ![]() is the actuarial notation for the probability that a person alive and insured at age
is the actuarial notation for the probability that a person alive and insured at age ![]() withdraws prior to age
withdraws prior to age ![]() in an environment where withdrawal is the only decrement, that is, that death is not possible. When the causes of censoring are other important decrements, an often-used assumption is that all the decrements are stochastically independent. That is, that they do not influence each other. For example, a person who withdraws at a particular age has the same probability of dying in the following month as a person who does not.
in an environment where withdrawal is the only decrement, that is, that death is not possible. When the causes of censoring are other important decrements, an often-used assumption is that all the decrements are stochastically independent. That is, that they do not influence each other. For example, a person who withdraws at a particular age has the same probability of dying in the following month as a person who does not.
![]()
Table 14.23 The single-decrement withdrawal probabilities for Example 14.24.
| j | |||||||
| 0 | 0 | 30 | 3 | 3 | 1 | 0 | |
| 1 | 29 | 0 | 1 | 2 | 0 | 0 | |
| 2 | 28 | 0 | 3 | 3 | 2 | 0 | |
| 3 | 26 | 0 | 3 | 3 | 3 | 0 | |
| 4 | 23 | 0 | 0 | 4 | 2 | 17 |
![]()
14.7.4 Exercises
- 14.43 Verify the calculations in Table 14.23.
- 14.44 For an anniversary-to-anniversary study, the values in Table 14.26 were obtained. Estimate
 and
and  using the exact Kaplan–Meier estimate, exact exposure, and actuarial exposure.
using the exact Kaplan–Meier estimate, exact exposure, and actuarial exposure.
Table 14.26 The data for Exercise 14.44.
d u x d u x 45 46.0 45 45.8 45 46.0 46 47.0 45 45.3 46 47.0 45 46.7 46 46.3 45 45.4 46 46.2 45 47.0 46 46.4 45 45.4 46 46.9 - 14.45 Twenty-two insurance payments are recorded in Table 14.27. Use the fewest reasonable number of intervals and an interval-based method with actuarial exposure to estimate the probability that a policy with a deductible of 500 will have a payment in excess of 5,000.
Table 14.27 The data for Exercise 14.45.
Deductible Paymenta Deductible Payment 250 2,221 500 3,660 250 2,500 500 215 250 207 500 1,302 250 3,735 500 10,000 250 5,000 1,000 1,643 250 517 1,000 3,395 250 5,743 1,000 3,981 500 2,500 1,000 3,836 500 525 1,000 5,000 500 4,393 1,000 1,850 500 5,000 1,000 6,722 aNumbers in italics indicate that the amount paid was at the policy limit. - 14.46 (*) Nineteen losses were observed. Six had a deductible of 250, six had a deductible of 500, and seven had a deductible of 1,000. Three losses were paid at a policy limit, those values being 1,000, 2,750, and 5,500. For the 16 losses not paid at the limit, one was in the interval (250,500), two in (500,1,000), four in (1,000,2,750), seven in (2 ,750,5,500), one in (5,500,6,000), and one in (6,000,10,000). Estimate the probability that a policy with a deductible of 500 will have a claim payment in excess of 5,500.
14.8 Maximum Likelihood Estimation of Decrement Probabilities
In Section 14.7, methods were introduced for estimating mortality probabilities with large data sets. One of the methods was a seriatim method using exact exposure. In this section, that estimator will be shown to be maximum likelihood under a particular assumption. To do this, we need to develop some notation. Suppose that we are interested in estimating the probability that an individual alive at age a dies prior to age b, where ![]() . This is denoted
. This is denoted ![]() . Let X be the random variable with survival function
. Let X be the random variable with survival function ![]() , the probability of surviving from birth to age x. Now let Y be the random variable X conditioned on
, the probability of surviving from birth to age x. Now let Y be the random variable X conditioned on ![]() . Its survival function is
. Its survival function is ![]() .
.
We now introduce a critical assumption about the shape of the survival function within the interval under consideration. Assume that ![]() for
for ![]() . This means that the survival function decreases exponentially within the interval. Equivalently, the hazard rate (called the force of mortality in life insurance mathematics) is assumed to be constant within the interval. Beyond b, a different hazard rate can be used. Our objective is to estimate the conditional probability q. Thus we can perform the estimation using only data from and a functional form for this interval. Values of the survival function beyond b will not be needed.
. This means that the survival function decreases exponentially within the interval. Equivalently, the hazard rate (called the force of mortality in life insurance mathematics) is assumed to be constant within the interval. Beyond b, a different hazard rate can be used. Our objective is to estimate the conditional probability q. Thus we can perform the estimation using only data from and a functional form for this interval. Values of the survival function beyond b will not be needed.
Now consider data collected on n individuals, all of whom were observed during the age interval ![]() . For individual j, let
. For individual j, let ![]() be the age at which the person was first observed within the interval and let
be the age at which the person was first observed within the interval and let ![]() be the age at which the person was last observed within the interval (thus
be the age at which the person was last observed within the interval (thus ![]() ). Let
). Let ![]() if the individual was alive when last observed and
if the individual was alive when last observed and ![]() if the individual was last observed due to death. For this analysis, we assume that each individual's censoring age (everyone who does not die in the interval will be censored, either by reaching age b or through some event that removes them from observation) is known in advance. Thus the only random quantities are
if the individual was last observed due to death. For this analysis, we assume that each individual's censoring age (everyone who does not die in the interval will be censored, either by reaching age b or through some event that removes them from observation) is known in advance. Thus the only random quantities are ![]() , and for individuals with
, and for individuals with ![]() , the age at death. The likelihood function is
, the age at death. The likelihood function is

where ![]() is the number of observed deaths and
is the number of observed deaths and ![]() is the total time the individuals were observed in the interval (which was called exact exposure in Section 14.7). Taking logarithms, differentiating, and solving produces
is the total time the individuals were observed in the interval (which was called exact exposure in Section 14.7). Taking logarithms, differentiating, and solving produces

Finally, the maximum likelihood estimate of the probability of death is ![]() .
.
Studies often involve random censoring, where individuals may exit for reasons other than death at times that were not known in advance. If all decrements (e.g. death, disability, and retirement) are stochastically independent (that is, the timing of one event does not influence any of the others), then the maximum likelihood estimator turns out to be identical to the one derived in this section. Although we do not derive the result, note that it follows from the fact that the likelihood function can be decomposed into separate factors for each decrement.
The variance of this estimator can be approximated using the observed information approach. The second derivative of the loglikelihood function is
Substitution of the estimator produces
and so ![]() . Using the delta method,
. Using the delta method,

Recall from Section 14.7 that there is an alternative called actuarial exposure, with ![]() with e calculated in a different manner. When analyzing results from this approach, it is common to assume that d is the result of a binomial experiment with sample size
with e calculated in a different manner. When analyzing results from this approach, it is common to assume that d is the result of a binomial experiment with sample size ![]() . Then,
. Then,
If the ![]() terms are dropped (and they are often close to 1), the two variance formulas are identical (noting that the values of e will be slightly different).
terms are dropped (and they are often close to 1), the two variance formulas are identical (noting that the values of e will be slightly different).
![]()
14.8.1 Exercise
- 14.47 In Exercise 14.44, mortality estimates for q45 and q46 were obtained by Kaplan–Meier, exact exposure, and actuarial exposure. Approximate the variances of these estimates (using Greenwood's formula in the Kaplan–Meier case).
14.9 Estimation of Transition Intensities
The discussion to this point has concerned estimating the probability of a decrement in the absence of other decrements. An unstated assumption was that the environment in which the observations are made is one where once any decrement occurs, the individual is no longer observed.
A common, and more complex, situation is one in which after a decrement occurs, the individual remains under observation, with the possibility of further decrements. A simple example is a disability income policy. A healthy individual can die, become disabled, or surrender their policy. Those who become disabled continue to be observed, with possible decrements being recovery or death. Scenarios such as this are referred to as multistate models. Such models are discussed in detail in Dickson et al. [28]. In this section, we cover estimation of the transition intensities associated with such models. The results presented are based on Waters [129].
For notation, let the possible states be ![]() and let
and let ![]() be the force of transition to state j for an individual who is currently between ages x and
be the force of transition to state j for an individual who is currently between ages x and ![]() and is in state i. This notation is based on an assumption that the force of transition is constant over an integral age. This is similar to the earlier assumption that the force of decrement is constant over a given age.
and is in state i. This notation is based on an assumption that the force of transition is constant over an integral age. This is similar to the earlier assumption that the force of decrement is constant over a given age.
![]()
While not shown here, maximum likelihood estimates turn out to be based on exact exposure for the time spent in each state. For those between ages x and ![]() (which can be generalized for periods of other than one year), let
(which can be generalized for periods of other than one year), let ![]() be the total time policyholders are observed in state i and
be the total time policyholders are observed in state i and ![]() be the number of observed transitions from state i to state j. Then,
be the number of observed transitions from state i to state j. Then, ![]() . Similarly,
. Similarly, ![]() .
.
![]()
The construction of interval-based methods is more difficult because it is unclear when to place the transitions. Those who make one transition in the year may be reasonably placed at mid-age. However, those who make two transitions would more reasonably be placed at the one-third and two-thirds points. This would require careful data-keeping and the counting of many different cases.

