1.1
Sentential Logic
1.1.1 Introduction
So what is mathematics? The word itself is derived from the Greek word mathēmatikē, meaning “knowledge” or “learning.” To both the practitioners of mathematics as well as the general public, the definition of the Queen of the Sciences varies widely.
- One of the greatest mathematician of Greek antiquity, Aristotle (384–322 BCE) defined mathematics as follows:
Mathematics is the science of quantity.
- Later, the Italian physicist Galileo (1564–1642), who was more interested in how it was applied, wrote:
“Mathematics is the language of the Universe and its characters are triangles, circles, and other geometric figures, without which it is impossible to understand a single word of it.”
- A more generic definition is given by the encyclopedia Britannica, which defines mathematics as follows:
Mathematics is the science of numbers and shapes and the relations between them.
- Then there is the beauty in mathematics as observed by the physicist Albert Einstein, who wrote
Pure mathematics is, in its way, the poetry of logical ideas.
- Iranian mathematician Maryam Mirzakhani once shared her thoughts about mathematics.
There are times when I feel like I'm in a big forest and don't know where I'm going, but then I come to the top of a hill and can see everything more clearly.
1.1.2 Getting into Sentential Logic
Although mathematics uses symbolic notation, its logical arguments are formulated in natural languages and so it becomes necessary to examine the truth value of natural language sentences. We begin by introducing the logical system behind reasoning called sentential (or propositional) logic, which is the most basic formal system of logic1 and uses symbols and rules of inference such as
if P is true and P implies Q, then Q is true2
Sentential logic is generally the first topic introduced in a formal study of logic, followed by more involved systems of logic, like predicate logic and modal logic.
English, as do all natural languages, contains various types of sentences, such as declarative, interrogative, exclamatory, and so on, which allow for the effective communication of thoughts and ideas. Some sentences are short and to the point, whereas others are long and rambling.
Some sentences can be classified as being either true or false, such as the sentence, “It will rain tomorrow.” Although we may not know if it will rain or not rain, the sentence is nevertheless either true or false.
Other sentences, like the interrogatory sentence, “Why doesn't Burger King sell hotdogs?” or the exclamatory sentence, “Don't go there!” express thoughts, but have no truth or false value. Although statements like these are useful for effective communication, they are no concern in our study of logic. The sentences we study in this book are declarative and are intended to convey information. In formal logic, the word “sentence” is used in a technical sense as described in the following definition.
1.1.3 Compound Sentences (“AND,” “OR,” and “NOT”)
In arithmetic, we combine numbers with operations +, × , −, and so on. In logic, we combine sentences with logical expressions. The sentences discussed thus far are examples of simple (or atomic) sentences since they are made up of a single thought or idea. It is possible to combine these sentences to form compound sentences using logical connectives.3
Table 1.1 Logical AND.
| P | Q | P ∧ Q | |
| T | T | T | P ∧ Q is true if both P and Q are true, otherwise false. |
| T | F | F | |
| F | T | F | |
| F | F | F |
Table 1.2 Logical OR.
| P | Q | P ∨ Q | |
| T | T | T | P ∨ Q is false if both P and Q are false, otherwise true |
| T | F | T | |
| F | T | T | |
| F | F | F |
Sometimes, in normal English discourse, the word “or” is used in an exclusive sense. For example, when someone says “for dessert I will have pie or cake,” it is normally understood to mean the person will have one of the two desserts, but not both. In this case, we would say “or” is an exclusive OR. In sentential logic, unless otherwise stated, “or” means the inclusive OR as defined in Table 1.2.
Table 1.3 Negation.
| P | ∼P | |
| T | F | ∼P is true when P is false, and ∼P is false when P is true. |
| F | T |
1.1.4 Compound Sentences
We can also combine sentences to form more complex sentences as illustrated in Table 1.4.
Table 1.4 Forming new sentences.
| P ∧ ∼ Q | Jack went up the hill but Jill did not. |
| ∼(P ∨ Q) | Neither Jack nor Jill went up the hill. |
| ∼(P ∧ Q) | It is not true both Jack and Jill went up the hill. |
| ∼P ∨ Q | Either Jack did not go up the hill or Jill did. |
The truth values of ∼P ∨ Q can be analyzed using the values in Table 1.5. The numbers above the columns give the order in which the truth values in the columns were filled.
Table 1.5 Truth table for ∼P ∨ Q.
| (1) | (2) | ||
| P | Q | ∼P | ∼P ∨ Q |
| T | T | F | T |
| T | F | F | F |
| F | T | T | T |
| F | F | T | T |
Note that ∼P ∨ Q is false only when P is true and Q is false, otherwise it is true.
The compound sentence (P ∨ Q) ∧ ∼ R contains three sentences P, Q, and R, and its truth value is determined by enumerating all 23 = 8 possible truth values for P, R, and R, followed by finding the truth values of the component parts of the sentence until arriving at the truth values of (P ∨ Q) ∧ ∼ R. These computations are shown in the truth table in Table 1.6.
Table 1.6 Truth table for (P ∨ Q) ∧ ∼ R.
| (1) | (2) | (3) | |||
| P | Q | R | P ∨ Q | ∼R | (P ∨ Q) ∧ ∼ R |
| T | T | T | T | F | F |
| T | T | F | T | T | T |
| T | F | T | T | F | F |
| T | F | F | T | T | T |
| F | T | T | T | F | F |
| F | T | F | T | T | T |
| F | F | T | F | F | F |
| F | F | F | F | T | F |
An example of a sentence containing four component sentences is (P ∧ Q) ∨ (R ∧ ∼ S), which depends on P, Q, R, and S. The truth value of this sentence is found by examining a truth table with 24 = 16 rows listing the 16 possible truth values of the four components. Table 1.7 shows how this truth table is computed.
Table 1.7 Truth table for (P ∧ Q) ∨ (R ∧ ∼ S).
| (1) | (2) | (3) | (4) | ||||
| P | Q | R | S | ∼S | P ∧ Q | R ∧ ∼ S | (P ∧ Q) ∨ (R ∧ ∼ S) |
| T | T | T | T | F | T | F | T |
| T | T | T | F | T | T | T | T |
| T | T | F | T | F | T | F | T |
| T | T | F | F | T | T | F | T |
| T | F | T | T | F | F | F | F |
| T | F | T | F | T | F | T | T |
| T | F | F | T | F | F | F | F |
| T | F | F | F | T | F | F | F |
| F | T | T | T | F | F | F | F |
| F | T | T | F | T | F | T | T |
| F | T | F | T | F | F | F | F |
| F | T | F | F | T | F | F | F |
| F | F | T | T | F | F | F | F |
| F | F | T | F | T | F | T | T |
| F | F | F | T | F | F | F | F |
| F | F | F | F | T | F | F | F |
1.1.5 Equivalence, Tautology, and Contradiction
In mathematics and in particular logic, the statement “means the same thing” is often used and has a precise meaning, which brings us to the concept of logical equivalence.
For example the sentences 1 + 1 = 3 and 10 < 5 are logically equivalent, the reason being they have the same truth value. The fact they have nothing to do with each other is irrelevant from the point of view of sentential logic, although the logical statements we study will be more useful. The following De Morgan's Laws are an example of two useful logical equivalences.
1.1.6 De Morgan's Laws
Two useful logical equivalences are De Morgan's Laws5 stated in Table 1.8.
Table 1.8 De Morgan's laws.
| De Morgan's laws |
| ∼(P ∨ Q) ≡ ∼ P ∧ ∼ Q |
| ∼(P ∧ Q) ≡ ∼ P ∨ ∼ Q |
Can you speak these equivalences in the language of Jack and Jill?
We can verify De Morgan's laws by making truth tables for each side of the equivalences. The top De Morgan Law6 in Table 1.8 is valid since columns (2) and (5) in Table 1.9 have T and F values for all truth/false values of P and Q.
Table 1.9 Verification of De Morgan's law.
| (1) | (2) | (3) | (4) | (5) | ||
| P | Q | P ∨ Q | ∼(P ∨ Q) | ∼P | ∼Q | ∼P ∧ ∼ Q |
| T | T | T | F | F | F | F |
| T | F | T | F | F | T | F |
| F | T | T | F | T | F | F |
| F | F | F | T | T | T | T |
 |
||||||
1.1.7 Tautology
The sentence P ∨ ∼ P is called the Law of the Excluded Middle and is a tautology since it is always true, regardless of the truth of its component parts. This is shown by the truth table in Table 1.10.
Table 1.10 Verification of a tautology.
| P | ∼P | P ∨ ∼ P |
| T | F | T |
| F | T | T |
The Law of the Excluded Middle is a principle that says everything is either true or false and nothing else. This seems an obvious and trivial concept, but this principle is fundamental when we study proofs by contradiction.
Table 1.11 Verification of a tautology.
| P | Q | P ∧ Q | ∼P | ∼Q | ∼P ∨ ∼ Q | (P ∧ Q) ∨ (∼P ∨ ∼ Q ) |
| T | T | T | F | F | F | T |
| T | F | F | F | T | T | T |
| F | T | F | T | F | T | T |
| F | F | F | T | T | T | T |
The opposite of a tautology is a contradiction.
An example of a contradiction is P ∧ ∼ P, as in “It is raining and it is not raining.” Regardless of the truth value of P, the truth value of P ∧ ∼ P is false. Many contradictions are obvious, while others are not so obvious. For example is the sentence (P ∧ ∼ Q) ∧ (Q ∧ R) always false regardless of the truth values of P, Q, and R? The answer is yes, and you might try to convince yourself of this fact without resorting to Table 1.12.
Table 1.12 Verification of a contradiction.
| (1) | (2) | (3) | (4) | |||
| P | Q | R | ∼Q | P ∧ ∼ Q | Q ∧ R | (P ∧ ∼ Q) ∧ (Q ∧ R) |
| T | T | T | F | F | T | F |
| T | T | F | F | F | F | F |
| T | F | T | T | T | F | F |
| T | F | F | T | T | F | F |
| F | T | T | F | F | T | F |
| F | T | F | F | F | F | F |
| F | F | T | T | F | F | F |
| F | F | F | T | F | F | F |
1.1.8 Logical Sentences from Truth Tables: DNF and CNF
Until now, we have found truth tables associated with various compound sentences. We now go backwards and find the logical expression that creates a given truth table. For example, what is the compound sentence that yields the truth table in Table 1.13.
Table 1.13 Three variable truth table.
| P | Q | R | ? | Row |
| T | T | T | T | 1 |
| T | T | T | F | 2 |
| T | T | F | F | 3 |
| T | T | F | T | 4 |
| T | F | T | T | 5 |
| T | F | T | F | 6 |
| T | F | F | T | 7 |
| T | F | F | F | 8 |
1.1.9 Disjunctive and Conjunctive Normal Forms
To find a logical sentence that yields a given truth table, there are two equivalent logical expressions that can be found, one called the disjunctive normal form and the other called the conjunctive normal form. These forms are defined as follows:
Simple examples are the following:

To find the DNF for the truth table in Table 1.13, we look at rows where the value of the truth table is TRUE, which are rows 1, 4, 5, and 7, then write the create formulas that yield a T. Doing this, we get
- row 1 true as a result that P ∧ Q ∧ R is true
- row 4 true as a result that P ∧ Q ∧ ∼ R is true
- row 5 true as a result that P ∧ ∼ Q ∧ R is true
- row 7 true as a result that P ∧ ∼ Q ∧ ∼ R is true
Hence, the truth table yields a T when at least one of the above conjunctions is true, which leads to the disjunctive normal form (DNF) for the truth table in Table 1.13.
To find the conjunctive normal form, we look at the rows where the truth table is FALSE, which are rows 2, 3, 6, and 8, which happens when the following are satisfied:
- row 2 is false when ∼P ∨ ∼ Q ∨ ∼ R
- row 3 is false when ∼P ∨ ∼ Q ∨ R
- row 6 is false when ∼P ∨ Q ∨ ∼ R
- row 8 is false when ∼P ∨ Q ∨ R
Hence, we have the conjunctive normal form for the truth table in Table 1.13:
You can verify that both the above disjunctive and conjunctive forms create the truth table in Table 1.13 and are thus logically equivalent. Conjunctive and disjunctive normal forms are important in circuit design where designs of integrated circuits are based on Boolean functions involving on/off switches.
Problems
- Simple Sentences
Which of the following are sentences?
- WE TAKE YOUR BAGS AND SEND THEM IN ALL
DIRECTIONS (posted at an airline ticket counter)
- The Riemann hypothesis is still unsolved.
- The Battle of Hastings was fought in 1492.
- The constant π is an algebraic number.
- DROP YOUR TROUSERS HERE FOR THE BEST
RESULT. (sign posted at a dry cleaners)
- The constant π is a transcendental number.
- I am a monkey's uncle.
- Never again!
- ABSOLUTELY NO SWIMMING
- 2 + 5 = 1
- e is an irrational number
- It is not true that 1 + 1 = 2.
- This sentence is false.

- Digit 0 does not appear in π.
- We sit on the porch watching cows playing Scrabble.
- The Chicago Cubs will win the World Series this year
- To be or not to be, that is the question.
- A woman, without her man, is nothing.
- A woman, without her, man is nothing.
- I think, therefore I am.
- All generalizations are false, including this one.
- These pretzels are making me thirsty.
- The fifth order polynomial equation has not been solved.
- Who was Niels Abel?
- WE TAKE YOUR BAGS AND SEND THEM IN ALL
- Truth Tables
For simple sentences P, Q, R make the truth table for the following compound sentences.
- P ∨ ∼ P
- P ∧ ∼ P
- P ∨ ∼ Q
- ∼P ∨ ∼ Q
- ∼(P ∨ Q)
- (P ∨ Q) ∧ R
- P ∧ (Q ∨ R)
- P ∨ (Q ∧ R)
- (P ∨ Q) ∨ (∼P ∨ ∼ Q)
- (P ∨ Q) ∧ (Q ∨ R)
- (P ∨ Q) ∨ (Q ∧ R)
- True or False
Let
- P be the sentence “4 > 2,”
- Q be the sentence “1 + 2 = 3”
- R be the sentence “5 + 2 = 9”
What is the truth value of the following compound sentences?
- P ∧ ∼ Q
- ∼(P ∧ Q)
- ∼P ∧ ∼ Q
- ∼(P ∨ Q)
- P ∧ Q
- (∼ P ∧ Q) ∨ P
- (∼ P ∧ Q) ∨ R
- (∼ R ∧ Q) ∨ R
- (∼ P ∨ Q) ∧ (P ∧ R)
- Tautologies and Contradictions
Suppose P and Q are sentences. Tell whether the following compound sentences are tautologies, contradictions, or neither. Verify your conclusion.
- P ∧ Q
- P ∨ Q
- Q ∨ ∼ Q
- P ∧ ∼ P
- P ∧ (Q ∨ ∼ P)
- P ∨ (Q ∧ ∼ P)
- In Plain English
In English, fill in the blanks in Table 1.14.
Table 1.14 Fill in the blanks.
The sentence Is TRUE when Is FALSE when P ∼P P ∨ Q P ∧ Q - Denial of Sentences
State the negation of each of the following sentences.
- π is a rational number.
- 317 is a prime number.
- The function f(x) = x2 + 1 has exactly one minimum.
- It will be cold and rainy tomorrow.
- It will be either cold or rainy tomorrow.
- It is not true that I am shiftless and lazy.
- It is not true that I am either lazy or shiftless.
- 2 is the only even prime number.
- Exclusive OR
In natural language the word “or” requires a certain amount of care. In this lesson we defined the word “or” in the inclusive sense, meaning one or the other or both. The exclusive or is slightly different; it means one or the other but not both
- Make a truth table for the exclusive or (denote it by ⊕)
- Verify that P ⊕ Q ≡ (P ∨ Q) ∧ ∼ (P ∧ Q).
- Prove or Disprove
Prove or disprove the statement
P ⊕ Q ≡ (P ∧ ∼ Q) ∨ (Q ∧ ∼ P)
where P ⊕ Q denotes the exclusive or, meaning P or Q are true but not both.
- Alternate Forms for Truth Tables
Truth tables for logical disjunction, conjunction and negation are analogous to addition, multiplication and negation in Boolean algebra, where 1 is defined as truth, 0 is taken as false, and minus as negation. Verify the following Boolean algebra statements in Figure 1.1 and find their logical equivalents in the sentential calculus.
- 1 + (−1) = 1
- 1 × (−1) = 0
- −(1 + 0) = 0 × 1
- −(0 × 1) = 1 + 0
- 1 × (1 + 0) = (1 × 1) + (1 × 0)
- 1 + (1 × 0) = (1 + 1) × (1 + 0)

Figure 1.1 Numeric truth table.
- Logical AND for IP Addresses
An IP address is a numerical label assigned to each device connected to a computer network. A typical IP address is a four‐dotted string of eight binary numbers (0s and 1s), which in decimal and binary form might be
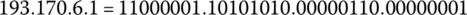
The network might consist of 10 computers connected to a router, where each computer in the network is assigned a subnet mask. If the subnet mask of one of the computers is

then the IP of this computer is the logical AND of the network IP and this subnet mask, which is the same as logical binary multiplication. What is the IP address of this computer using binary arithmetic 0 ⋅ 0 = 1, 0 ⋅ 1 = 0, 1 ⋅ 0 = 0, 1 ⋅ 1 = 1?
Show that this sentence is a tautology.
- Disjunctive and Conjunctive Normal Forms
Find disjunctive and conjunctive normal forms that create the following truth tables.
- Syllogisms
In Aristotelian logic,8 a syllogism is an argument in which two premises (which are assumed true) lead to a valid conclusion. The most general form being

An example would be

In the language of sentential logic, this syllogism takes the form
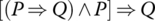
Show that this sentence is a tautology.
- Digital Logical Circuits I
Find the truth table for each of the following digital logical circuits in Figure 1.2 to prove they are equivalent. What logical law does the equivalence of these circuits represent? The individual electronic components are self‐explanatory.

Figure 1.2 Logical circuit.
- Digital Logical Circuits II
Find the truth table for each of the following digital logical circuits in Figure 1.3 to prove they are equivalent. What logical law does the equivalence of these circuits represent? The individual electronic components are self‐explanatory.

Figure 1.3 Logical circuit.
- Internet Research
There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward sentential logic, first‐order‐logic, liar paradox, de Morgan's laws, and disjunctive normal form.
Notes
- 1 There are other formal systems of logic other than sentential (or propositional) logic, such as predicate and modal logic. Because the rules of formal logic are precise, they can be programmed for a computer and are capable of analyzing mathematical proofs. Formal logical systems are important in artificial intelligence, where computers are programmed in the language of formal logic to carry out logical reasoning.
- 2 Greek logicians called this rule of inference modus ponens, meaning the way that affirms.
- 3 We can also combine compound sentences to form more complex sentences.
- 4 We are getting a little ahead of ourselves, but we will get to sets in Chapter 2.
- 5 Augustus De Morgan (1806–1871) was an Indian‐born British mathematician and logician who formulated what we call De Morgan's Laws. He was the first person to make the idea of mathematical induction rigorous.
- 6 This De Morgan law says the negation of a disjunction is the conjunction of its negatives.
- 7 In natural language, a tautology is often thought of as a sentence that says the same thing twice in a different way.
- 8 This form of a syllogism is but one of several devised by the Greek philosopher Aristotle (384 B.C. 322 BCE). Aristotle, along with Plato and Socrates, are three of the most important founding figures of Western philosophy and thought.
