2.5
Uncountable Sets
2.5.1 Introduction
Thus far, the only infinity considered has been countable infinity, which is the cardinality of the natural numbers or any set of many sets that can be written as a sequence. This begs the question are all infinite sets equivalent to the natural numbers? In 1874, the German mathematician Georg Cantor proved that there are in fact sets with even larger cardinalities than of the natural numbers, which led to the development of modern set theory.
At the time Cantor believed, as did all mathematicians, that infinity was infinity. Thinking along those lines, Cantor tried to prove that the real numbers have the same cardinality as the natural numbers, but failed and his failure was one of the greatest failures in the history of mathematics since in the process he proved that the real numbers have a larger cardinality than that of the natural numbers.
Table 2.13 Hypothesized one‐to‐one correspondence ℕ ↔ (0, 1).
| ℕ | (0, 1) | ||||||||||||||
| ↓ | ↓ | ||||||||||||||
| 1 | ↔ | 0 | . | 1 | 4 | 3 | 2 | 0 | 2 | 8 | 1 | 4 | … | ||
| 2 | ↔ | 0 | . | 3 | 5 | 5 | 4 | 4 | 4 | 6 | 2 | 6 | … | ||
| 3 | ↔ | 0 | . | 6 | 3 | 0 | 3 | 5 | 3 | 4 | 1 | 5 | … | ||
| 4 | ↔ | 0 | . | 8 | 7 | 8 | 7 | 3 | 5 | 5 | 3 | 3 | … | ||
| 5 | ↔ | 0 | . | 0 | 5 | 8 | 6 | 5 | 8 | 8 | 7 | 5 | … | ||
| 6 | ↔ | 0 | . | 4 | 9 | 6 | 5 | 8 | 7 | 7 | 5 | 4 | … | ||
| … | … | . | … | … | … | … | … | … | … | … | ⋱ | ||||
To show how Cantor creates a “rogue” real number 0. a1a2a3… not on the list in Table 2.13, Cantor picks the first digit a1different from the first digit of the real number corresponding to 1 (i.e. the number 0.143 202 814…). In other words, pick a1 anything other than 1, say a1 = 3. See Table 2.14. Now select the second digit a2 anything other than the second digit of the real number corresponding to the 2. So we select a2 different from 5, which we (randomly) pick a2 = 2.
Continuing this process, working down the diagonal of the table, the first six digits of our rogue number might be 0.327 245… and continuing this process indefinitely, we arrive at a real number that does not correspond to any natural number. Hence, the assumed one‐to‐one correspondence f : ℕ → (0, 1) described in Table 2.14 is not a one‐to‐one correspondence between ℕ and (0, 1) since we have found an element of (0, 1) that does not correspond to any natural number. Thus we conclude that the open interval (0, 1)has a larger cardinality than the natural numbers, or |ℕ| < |(0, 1)|.▌
Table 2.14 Cantor's diagonalization process.
| ℕ(0, 1) | |||||||||||||||
| ↓↓ | |||||||||||||||
| 1 | ↔ | 0 | . | [1] | 4 | 3 | 2 | 0 | 2 | 8 | 1 | 4 | … | ||
| 2 | ↔ | 0 | . | 3 | [5] | 5 | 4 | 4 | 4 | 6 | 2 | 6 | … | ||
| 3 | ↔ | 0 | . | 6 | 3 | [0] | 3 | 5 | 3 | 4 | 1 | 5 | … | ||
| 4 | ↔ | 0 | . | 8 | 7 | 8 | [7] | 3 | 5 | 5 | 3 | 3 | … | ||
| 5 | ↔ | 0 | . | 0 | 5 | 8 | 6 | [5] | 8 | 8 | 7 | 5 | … | ||
| 6 | ↔ | 0 | . | 4 | 9 | 6 | 5 | 8 | [7] | 7 | 5 | 4 | … | ||
| … | … | … | … | … | … | … | … | … | … | … | … | … | |||
| … | … | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | … | … | … | … | |||
| … | … | 0 | . | 3 | 2 | 7 | 2 | 4 | 5 | … | … | … | … | ||
You may now ask what other sets have the cardinality of the continuum. The answer will surprise you.
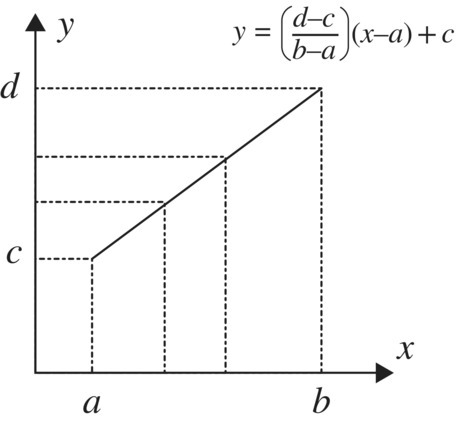
Figure 2.30 Equivalence of two intervals of real numbers.
2.5.2 Cantor's Surprise
Cantor had not finished surprising the mathematics world with his discovery of more than one kind of infinity. It completely destroyed previous thinking that “infinity was infinity.” Cantor's next project was to prove there are more points in the plane than there are real numbers, and again Cantor failed, and again his failure made another monumental discovery. Cantor worked tirelessly from 1871 to 1874 to prove the cardinality of the plane is greater than the cardinality of the real line, but to his amazement he proved they are the same. In a letter to his good friend Richard Dedekind, he said, “I see it, but I don't believe it.” Here is a summary of Cantor's proof.
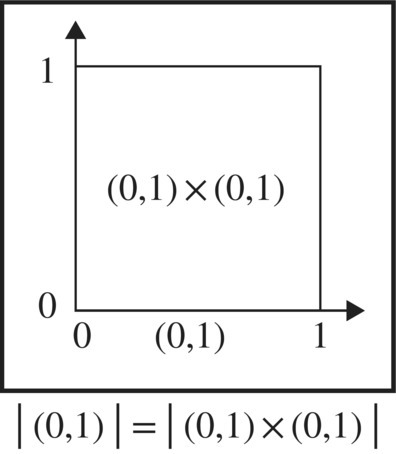
Figure 2.32 |(0, 1)| = |(0, 1) × (0, 1)|.
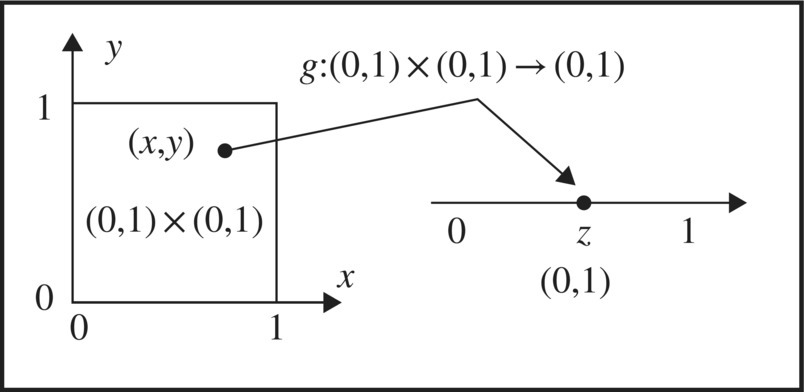
Figure 2.33 One‐to‐one map showing |(0, 1) × (0, 1)| ≤ |(0, 1)|.
2.5.2.1 Cardinality of the Irrational Numbers
The interval (0, 1) is the disjoint union of rational and irrational numbers. Since the interval (0, 1) has cardinality c and the rational numbers have cardinality ℵ0 and the union of two countably infinite sets is countably infinite, this implies that the irrational numbers have cardinality c. In other words, there are more irrational numbers than rational numbers.
2.5.2.2 Algebraic and Transcendental Numbers
A number x is called a real algebraic number if it is a real root of a polynomial 4 equation
where the coefficients ak ' s are integers. The irrational number ![]() is an example of an algebraic number being a root of x2 − 2 = 0. Numbers that are not algebraic are called transcendental. One would guess there are more algebraic numbers than transcendental numbers since the first transcendental number, called the Liouville constant after who had discovered it, was only discovered in 1851. It was later discovered that π and Euler's constant e are also transcendental. Later, Cantor shocked the mathematical world when he proved there are more transcendental numbers than algebraic ones.
is an example of an algebraic number being a root of x2 − 2 = 0. Numbers that are not algebraic are called transcendental. One would guess there are more algebraic numbers than transcendental numbers since the first transcendental number, called the Liouville constant after who had discovered it, was only discovered in 1851. It was later discovered that π and Euler's constant e are also transcendental. Later, Cantor shocked the mathematical world when he proved there are more transcendental numbers than algebraic ones.
Table 2.15 Polynomial equations of A10 and their roots.
| k | Polynomial equation Pk(x) = 0 | # Equations | # Roots |
| 1 | P1(x) = x + a0 = 0 | 2n + 1 = 21 | 1 ⋅ (2n + 1) = 21 |
| 2 | P2(x) = x2 + a1x + a0 = 0 | (2n + 1)2 = 212 | 2 ⋅ (2n + 1)2 = 2 ⋅ 212 |
| 3 | P3(x) = x3 + a2x2 + a1x + a0 = 0 | (2n + 1)3 = 213 | 3 ⋅ (2n + 1)3 = 3 ⋅ 213 |
| ⋯ | ⋯ | ⋯ | ⋯ |
| 10 | P10(x) = x10 + a9x9 + ⋯ + a1x + a0 = 0 | (2n + 1)10 = 2110 | n ⋅ (2n + 1)10 = 10 ⋅ 2110 |
The fact that the algebraic numbers are countable implies the transcendental numbers are uncountable since if the transcendental numbers were countable that would imply the real numbers would also be countable being the union of countable sets. But the real numbers are uncountable and so the transcendental numbers must be uncountable.
Problems
- Which of the following sets are finite, countable, or uncountable?
- [0, 1] ∩ ℕ
- {ℕ, ℤ, ℚ, ℝ, ℂ}
- {1/n : n ∈ ℕ − {0}}
- {x ∈ ℝ : x2 + 1 < 0}
- The set of all 2 by 2 matrices with natural numbers for elements.
- Cardinality of Functions
Show that the cardinality of the set of functions F = {f : ℕ → ℕ} is uncountable.
- Irrational Numbers
Show that the irrational numbers in the interval [0, 1] is uncountable.
- Algebraic Numbers
Show that the numbers
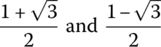
are algebraic numbers.
- Countable Plus Singleton
Prove that if we add a member to a countable set A, we still have a countable set.
- Proving Cardinality (ℝ ≈ ℝ3)
Show that the unit cube
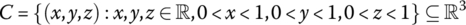
is equivalent to the unit interval (0, 1) ⊆ ℝ. Hint: Use the technique Cantor used to prove (0, 1) is equivalent to the unit square.
- Liouville Constant
Some famous transcendental numbers are π, e, eπ, πe, ln 2, ….The first provable transcendental number was found 1851 by the French mathematician Joseph Louiville (1809–1882), who constructed and proved the constant

is transcendental. Write out the first few decimal digits of this number. Google “Liouville's constant” and read more about it.
- Irrational Numbers
Prove or disprove. There exists a countably infinite subset of the irrational numbers.
- Internet Research
There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward uncountable set, Cantor's diagonization proof, and examples of uncountable sets.
