Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

3.2
Order Relations

3.2.1 Let There Be Order

The British philosopher Edmund Burke once said, “Order is the foundation of all that is good,” and although he probably was not referring to inequalities of numbers, nevertheless, order is as important in mathematics as it is anywhere else. The reader is familiar with the inequality relations ≤ and < that impose an ordering of real numbers, and the relation ⊆, which imposes an “order” on sets. Other objects can be “ordered” as well, such as functions, matrices, and points in the plane. Ordering objects according to given rules brings structure to an area that might otherwise be difficult to analyze. In computer science, order not only brings understanding, but efficiency. Imagine trying to find information on the Internet if search engines did not have clever “ordering” strategies for searching for information.

Definition Simple, Partial, and Strict Order

A partial order on a set A, denoted by ≤, is a binary relation on A such that for all x, y, z in A, the following RAT conditions hold.

When a partial order is defined on a set, the set is said to be partially ordered or a partially ordered set. When x ≤ y, we say x precedes y. The usual “less than or equals to” is a prime example of a partial order on the real numbers.
A strict order, denoted by <, is a binary relation on a set A such that for all x, y, z of A, the following IAT conditions hold.

When a strict order is defined on a set, the set is said to be strictly ordered or a strictly ordered set. The usual “less than” inequality (<) is a prime example of a strict order on the real numbers, and we would say the real numbers are strictly ordered by the less than order.

Both partially ordered and strictly ordered sets are said to be totally ordered if every two members of the set are comparable. The usual “less than or equal to” order (≤) is a total order on the real numbers since any two real numbers x, y satisfy x ≤ y or y ≤ x. On the other hand, the set inclusion relation (⊆) is a partial order on the power set P(A) of A = {a, b, c}, but does not totally order the power set since not all sets in the power set are comparable, an example being the sets {a, c} and {b}.

Image described by caption. — **Figure 3.10** Picturing partial orders (a) graphs, (b) arrow illustration, and (c) directed graph.

Example 3 Ordering by Division Property

Let “∣” denote the relation “divides” on the set of natural numbers ℕ. For example, 1 ∣ 7, 2 ∣ 8, 3 ∣ 9, 7 ∣ 21. If m does not divide n, we denote this by as in . Show that “∣” defines a partial order on the natural numbers.

Solution

We show that division is reflexive, antisymmetric, and transitive.

Reflexive [n ∣ n]: The relation is reflexive since natural numbers divide themselves.
Antisymmtric: We must show

Using what it means for one number to divide another, we write

so we have

which implies k₂k₁ = 1, and since k₁ and k₁ are positive integers, we have the relation k₁ = k₂ = 1, which implies m = n.
Transitive: We must prove

Using what it means for one number to divide another, we write

Hence,

which implies m ∣ p.

3.2.2 Total Order and Symmetric Relations

Although, we have seen that “≤” and “⊆” are partial orders on ℝ and P(A), respectively, there is an important difference. The partial order “≤” on the real numbers is also a total order, inasmuch as any two real numbers x and y are comparable as in x ≤ y or y ≤ x. On the other hand, “⊆” is not a total order on the power set of {a, b, c} since it is not true that

{a, c} ⊆ {a, b} or {a, c} ⊇ {a, b}.

3.2.3 Symmetric Relation

We say a relation R on a set A is symmetric if xRy ⇔ yRx for all x, y ∈ R. One might think offhand that antisymmetry is the negation of being symmetric, but this is not true. The equal relation “=” is both symmetric and antisymmetric. However, the relation “is married to” is a symmetric relation but is not antisymmetric, whereas the relation ≤ on the real line is antisymmetric but not symmetric.

3.2.4 Hasse Diagrams and Directed Graphs

Although a partially ordered set can contain an infinite number of elements, many important examples are finite. A useful way to represent finite partially ordered sets is a Hasse Diagram,¹ where each element of the ordered set is denoted by a dot (node) and a line segment that goes upward from node x to node y means that x ≤ y.

A Hasse diagram for a partial order on A = {a, b, c, d, e, f, g} is drawn in Figure 3.11, where a few orderings are e ≤ d, f ≤ d, g ≤ d. Also e ≤ c by transitivity since one can move upwards from e to c moving through the nodes d and b. On the other hand, and , so the order is not a total order since some elements are not comparable.

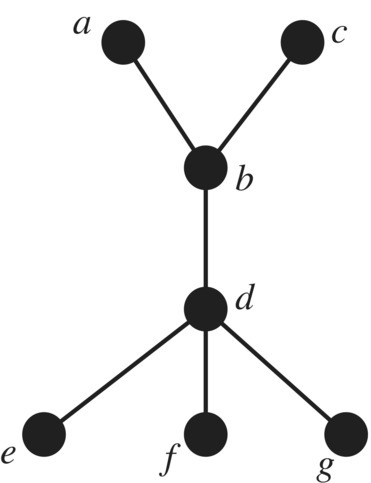
Hasse diagram displaying connected solid circles labeled a, b, c, d, e, f, and g. — **Figure 3.11** Hasse diagram.

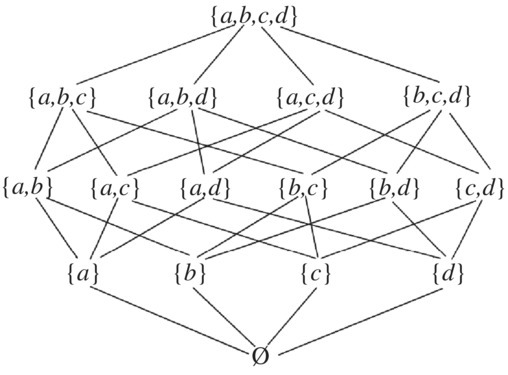
Hasse diagram for the power set of four elements from {a,b,c,d} with lines connecting to {a,b,c}, {a,b,d}, {a,c,d}, {b,c,d}, {a,b}, {a,c}, {a,d}, {b,c}, {b,d}, {c,d}, {a}, {b}, {c}, {d} leading to Ø. — **Figure 3.13** Hasse diagram for the power set of four elements.

3.2.5 Upper Bounds, Lower Bounds, glb, and lub

Definition

Let ≤ be a partial order on a set U and S ⊆ U a subset of U.

Upper Bound of S: An element u ∈ U is an upper bound of S if and only if (∀s ∈ S)(s ≤ u).
Least Upper Bound (lub) of S: An element lub(S) ∈ U is the least upper bound (or supremum) of S if lub(S) it is an upper bound for S and lub (S) ≤ u for every other upper bound u of S.
Lower Bound: An element l ∈ U is a lower bound of S if and only if (∀s ∈ S)(l ≤ s).
Greatest Lower Bound (glb): An element glb (S) ∈ U is the greatest lower bound (or infimum) of S if glb (S) is a lower bound for S and l ≤ glb (S) for every other lower bound l of S.
Maximum and Minimum: An element M ∈ S is the maximum element of S if and only if

An element m ∈ S is the minimum element of S if and only if
Maximal Element: An element M ∈ S is a maximal element of S if and only if

In other words, a maximal element is an element of the set that is not “smaller” than any other member of the set.
Minimal Element: An element m ∈ S is a minimal element of S if and only if

In other words, a minimal element is an element of the set such than no other member is “less” than the minimal member. See Figure 3.14.

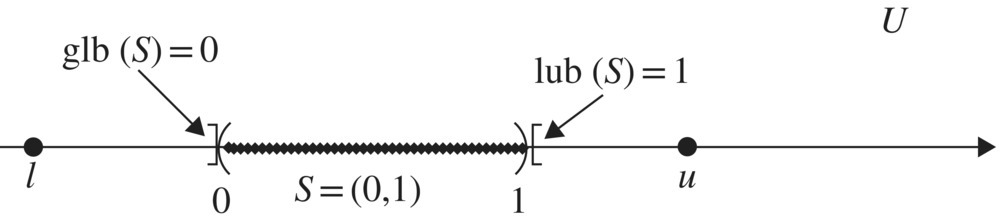
Diagram of ordering properties displaying right arrow with solid circle markers labeled l and u, left and right bracket labeled lub (S)=1 and glb (S)=0 respectively, and broad line labeled S=(0,1) enclosed by parenthesis. — **Figure 3.14** Ordering properties.

Hasse diagram partial order displaying solid circles labeled A, B, C, D, E, F, G, H, I, J, K, L, M, N, and O connected with solid lines. — **Figure 3.15** Hasse diagram partial order.

Table 3.2 lists some common relations and their properties. The set over which the relation is defined is given in parenthesis next to the relation.

Table 3.2 Properties of common relations.

	Reflexive	Antisymmetric	Transitive	Symmetric
Relations	xRx	xRy ∧ yRx ⇒ x = y	xRy ∧ yRz ⇒ xRz	xRy ⇒ xRx
≤ (ℝ)	Yes	Yes	Yes	No
< (ℝ)	No	No	Yes	No
≡ (mod n)	Yes	No	Yes	Yes
≈ (sets)	Yes	No	Yes	Yes
⊆ (sets)	Yes	Yes	Yes	No
⊥ (lines)	No	No	No	Yes
∥ (lines)	Yes	No	Yes	Yes
∣ on ℤ	Yes	No	Yes	No
∣ on ℕ	Yes	Yes	Yes	No
= (ℝ)	Yes	Yes	Yes	Yes

Problems

Testing for an Order Relation
Tell whether the following relations on A = {1, 2, 3} are reflexive, antisymmetric, and transitive. Plot the points of the relation in the Cartesian product A × A and denote the members of R ⊆ A × A. If the relation is an order relation, draw a Hasse diagram and directed graph for the relation.
1. R = {(1, 1), (2, 2), (3, 3)}
2. R = {(1, 1), (1, 2), (2, 1)}
3. R = {(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)}
4. R = {(1, 2), (2, 3), (1, 3)}
Finding Relations
Find a relation on A = {1, 2, 3, 4} with the following properties.
1. Reflexive, but not antisymmetric
2. antisymmetric and reflexive
3. not reflexive, but transitive
4. not reflexive, not antisymmetric, not transitive
Ordering of Functions
Let C[0, 1] be the set of continuous functions defined on [0, 1]. For f, g ∈ C[0, 1], define the ordering

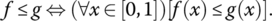
Show that “≤” defines a partial order on C[0, 1].
Upper and Lower Bounds
The Hasse diagram for the power set P(A) of A = {a, b, c, d} is drawn in Example 6 with order relation ⊆. Use the Hasse diagram to find an upper bound, a least upper bound, a lower bound, and the greatest lower bound of the following subsets of P(A)
1. B = {{a}, {a, b}}
2. B = {{a}, {b}}
3. B = {{a}, {a, b}{a, b, c}}
4. B = {{a}, {c}, {a, c}}
5. B = {Ø, {a, b, c}}
6. B = {{a}, {b}, {c}}
Sups and Infs
If they exist, find the sup, inf, max, and min of the following sets.
1. (− ∞ , 2)
2. (− ∞ , 2]
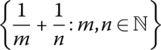
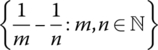
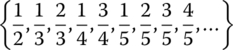6. (omit fractions not in reduced form)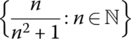
8. {y : y = x² + x − 2, x ∈ ℝ}

Hasse Diagram

Jane is getting a degree in mathematics and has several courses to take. Some of the courses have prerequisites as shown below.

Course needed	Prerequisites
Calculus I
Calculus II	Calculus I
Calculus III	Calculus II
Linear Algebra	Calculus III
Differential Equations	Calculus III
Intro to Pure Math	Linear Algebra, Calculus II
Abstract Algebra	Linear Algebra, pure math
Advanced Calculus	Calculus III, pure math

Draw a Hasse diagram that illustrates the order which Jane must take courses.

Hasse Diagram for Multiples
Let M be the order relation “a is a multiple of b” defined on the positive divisors of 15. Draw a Hasse diagram for M.
A Partial Order for Points in the Plane
There are various ways to construct new orders from existing orders. A partial order can be constructed on the Cartesian product of two partially ordered sets by defining
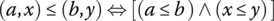
1. Construct a Hasse diagram that represents a partial order for
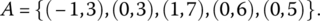
2. Draw a directed graph for the partial order.
Equivalent form of Antisymmetry
State the contrapositive form of the antisymmetry condition
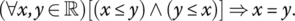
Ordering the Complex Numbers
Suppose we try to order the complex numbers z = a + bi according to magnitudes

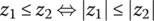
where 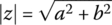is the magnitude of the complex number. Is this a partial order on the complex numbers?
Total Order of the Complex Numbers
The complex numbers can be totally ordered as follows. Given two complex numbers in polar form

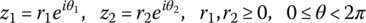
order the complex numbers by

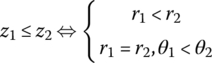
Compare the following complex numbers.
1. z₁ = i, z₂ = 1 + i
2. z₁ = i, z₂ = − 1
3. z₁ = 6i, z₂ = 2 + 3i
4. z₁ = 0, z₂ = 1
Counting Partial Orders
There are a total of three partial orders on A = {1, 2}. Can you find them?
Hasse Diagram
Given the subset S ⊆ U represented by “stars” in the Hasse diagram in Figure 3.17 which describes a partial ordering of the set:

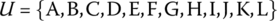
find the following quantities of S:
1. upper bound(s)
2. lower bound(s)
3. the least upper bound
4. greatest lower bound
5. maximal element(s)
6. minimal element(s)
7. maximum
8. minimum
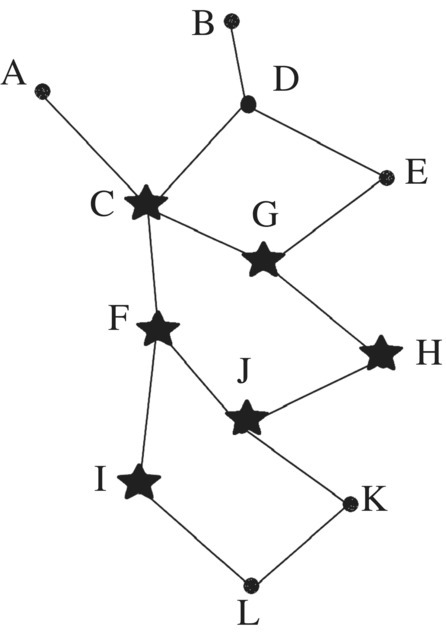
Figure 3.17 Hasse diagram.
Test Your Knowledge of Sups and Infs
A Hasse diagram representation of a partial order is shown in Figure 3.18. If they exist, find the sup and inf of the following sets. A partially ordered set is called a lattice if every pair of elements in the set has a sup and inf. Is the set under this partial order a lattice?
1. {2, 3}
2. {8, 9}
3. {1, 2}
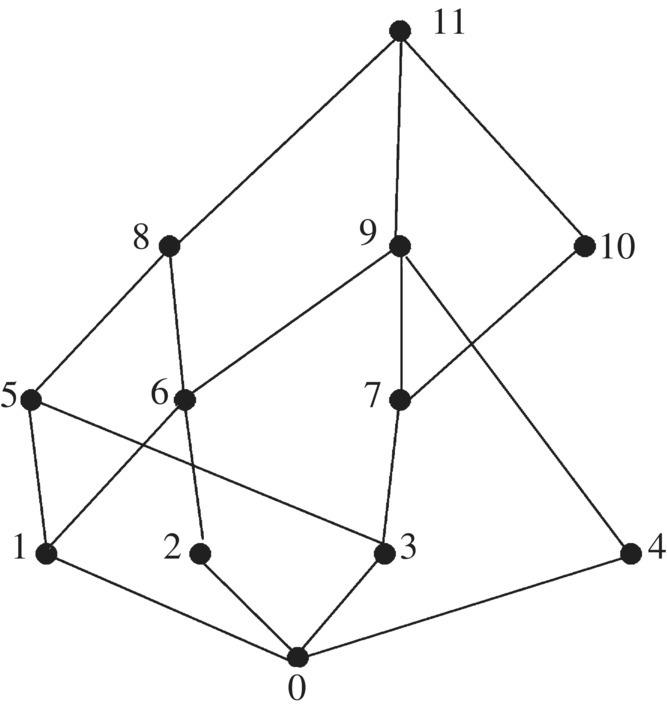
Figure 3.18 Sups and Infs.
SUP or MAX?
If it exists, find the maximum value of the set

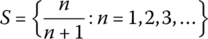
If it does not exist, find the least upper bound of S.
Lattices
A lattice L is a partially ordered set in which every two members a, b ∈ L has a supremum and infimum in L. The supremum is called the join of aand b and denoted by a ∨ b, and the infimum is called the meet of a and b, and denoted by a ∧ b. Determine which of the partially ordered sets in Figure 3.19 represented by Hasse diagrams, are lattices.

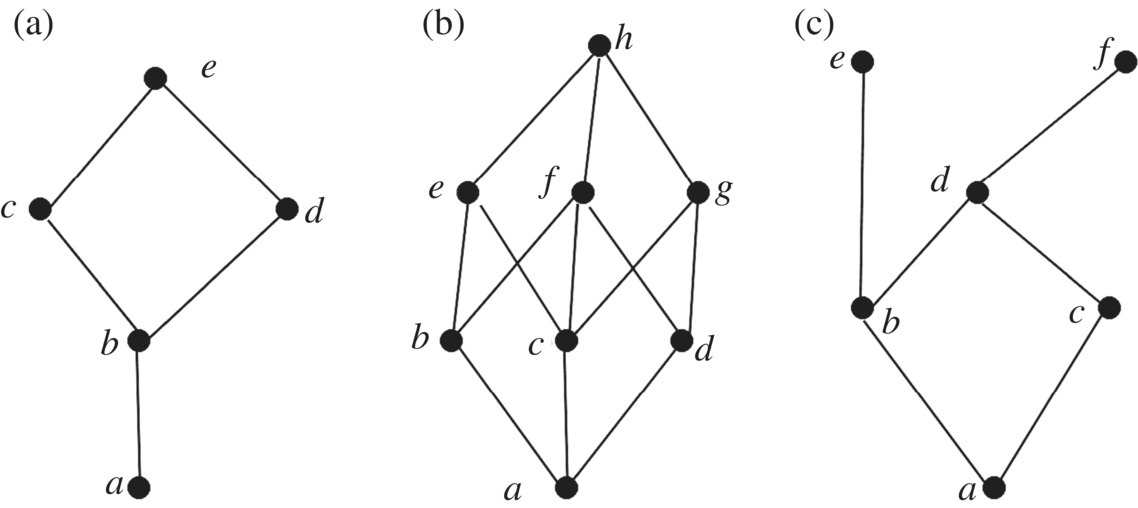
Figure 3.19 Lattice or non lattice.
Lattice of Partitions
A lattice is a partially ordered set in which every two elements has a unique least upper bound (called their join) and a unique greatest lower bound (called their meet.) Figure 3.20 shows a Hasse diagram for the set of all partitions of {1.2.3.4} into disjoint subsets, partially ordered by “increasing merging of sets.” The slashes between numbers represent different partitions. For instance 1/2/3/4 means the partition {1}, {2}, {3}, {4} and 14/23 denotes the partition {1, 4}, {2, 3}. Draw the lattice for the set of partitions of the set {a, b, c}.

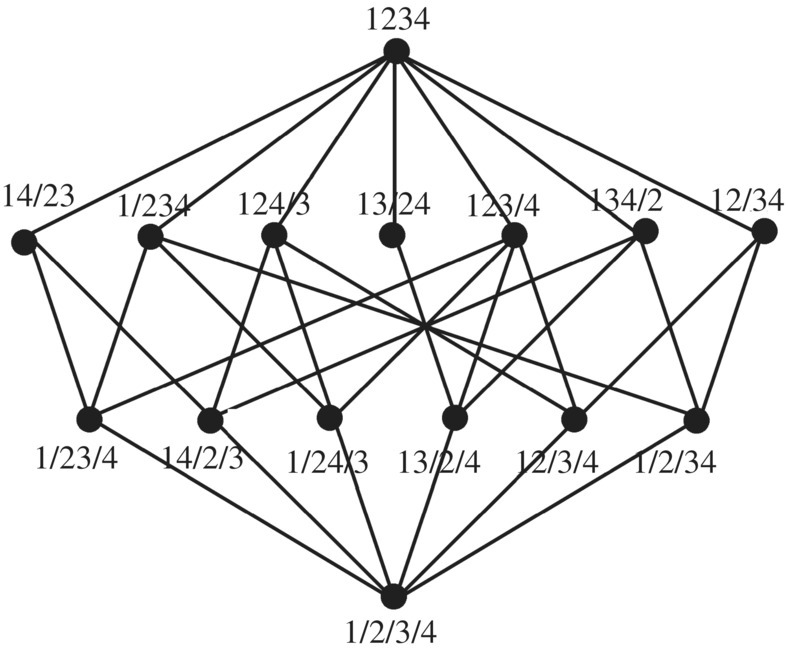
Figure 3.20 Lattice of partitions.
True or False
Assuming the usual partial ordering ≤ for the rational and real numbers, tell which of the following are true or false.
1. Every partially ordered set has a least upper bound.
2. Every set that is bounded above has a least upper bound.
3. Every set of rational numbers bounded above has a least upper bound.
4. Every set of real numbers that is bounded above has a least upper bound.
Dense Orders
A partial order R on a set A is said to be dense in A if

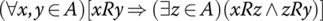
Which of the following partial orders are dense on the given set?
1. “less than or equal to” ≤ on the rational numbers.
2. “is a subset of” ⊆ on a power set P(A).
3. “less than” < on the real numbers ℝ.
4. “is younger than” on a collection of people.
Inverse of a Partial Order
If R is a partial order on a set A, then show the inverse R⁻¹ relation is a partial order on A.
An Upper Bounded Set with No Sup
Show that the set

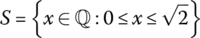
is bounded above but has no least upper bound.
Composition of Partial Orders
Let R be the usual “less than or equal to” ordering and S be the usual “greater than or equal to” ordering on the set A = {1, 2, 3}. Find the composition R ∘ S = ≤ ∘ ≥ of the two orders.
Partitions of a Natural Number²
A partition of a positive integer is a way of writing the number as a sum of positive integers where the order is not important and numbers can be repeated. The five partitions of the number 4 are shown in Figure 3.21.

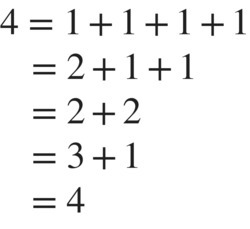
Figure 3.21 Partition of 4.

The function that gives the number of partitions of a natural number n is called the partition function p(n), and in this case p(4) = 5. A convenient way to organize the partitions on a number is a Ferrers diagram, where the number of rows in the diagram represent the number of terms in the partition and the number of squares in the row is the size of the term. The Ferrers diagram for the partitions of numbers 1–5 is shown in Figure 3.22. Find the partitions of 6 and draw the Ferrers diagram.

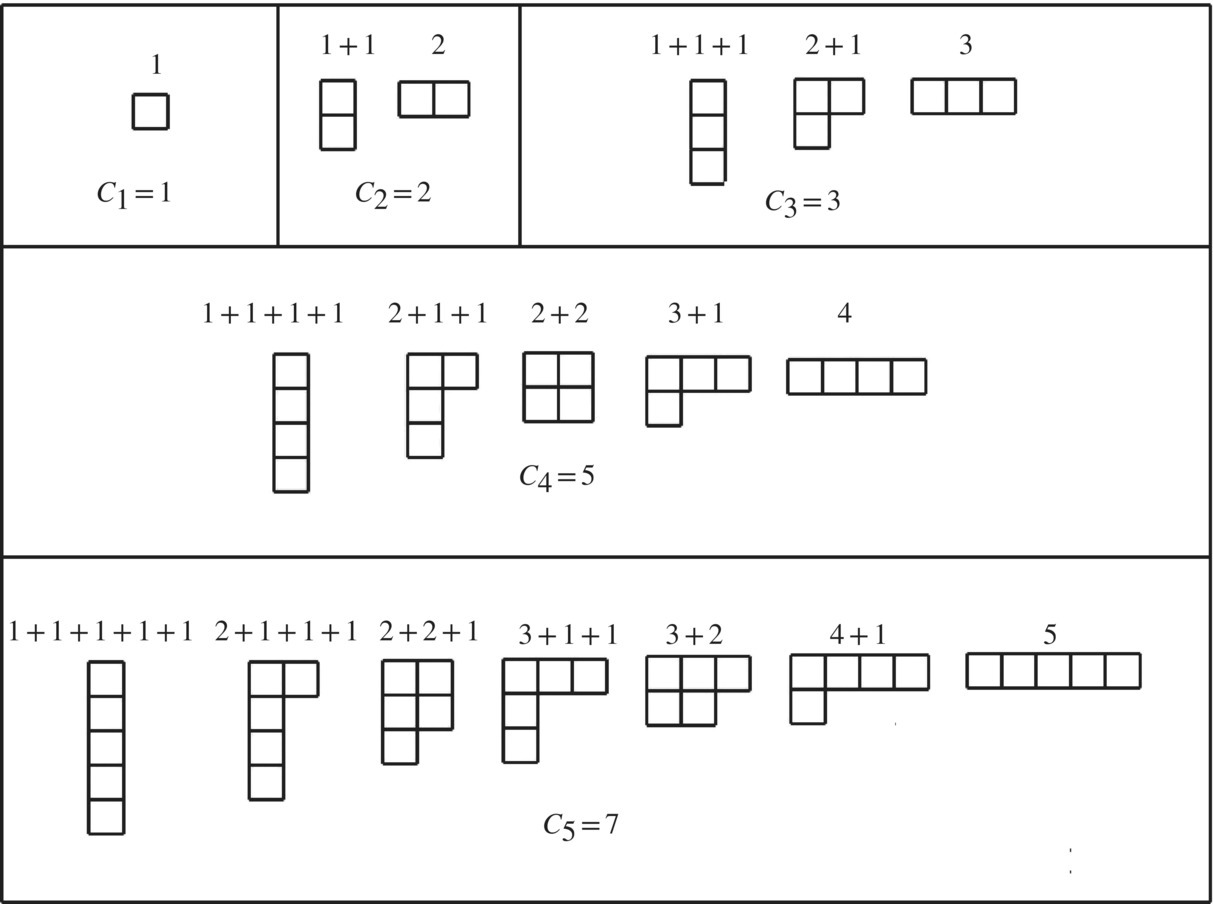
Figure 3.22 Ferrers diagram.

An asymptotic estimate for p(n) was found in 1918 by G.H. Hardy and Ramanujan to be

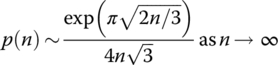
Use this formula to estimate p(100), p(200), p(1000).
Internet Research
There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward ordered structures in math, ordered sets.

Notes

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 3.2 Order Relations

Create new playlist

Sign In

Sign Up