5.3
Geometric Topology
5.3.1 Introduction
It is instructive to compare a geometer with a topologist. For a geometer, the pattern of ridges on your fingers and palms are too amorphous for serious analysis. There are no lines, circles, or other geometric shapes which geometers love. On the other hand, a topologist is not restricted to the rigid shapes of Euclidean geometry, but studies more general patterns and classifies them according to specific topological rules. See Figure 5.49.
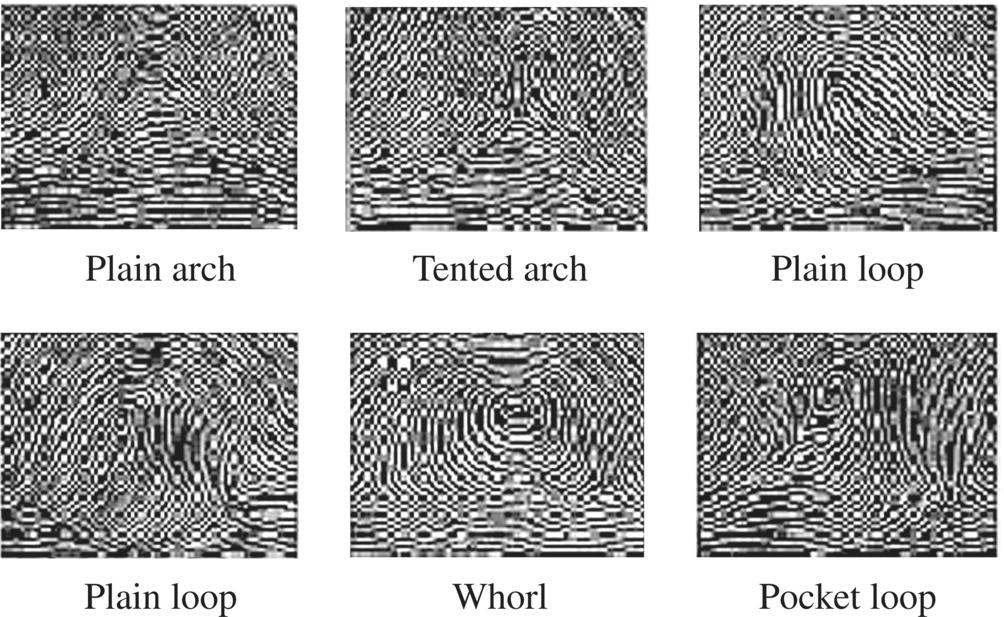
Figure 5.49 Topological fingerprints.
When a topologist looks at the ridges on your fingers and palms, the topologist sees nearly parallel curves, which is nature's way of preferring order and continuity, but when ridges collide things get complicated. Ridges come together in a variety of interesting, often unexpected ways, and it is the job of a topologist to classify the ways this can occur. You may not have had an interest in topology at this stage in your life, but the ridges on your fingers provide a lesson in basic topology.
The study of topology is not just about vertices and edges studied in the previous two sections on graphs, or even about one‐dimensional fingerprints, but extends to surfaces in higher dimensions 2, 3, 4, …, where the standard rules of Euclidean geometry are relaxed, yielding an exciting new geometry, what some call “rubber‐sheet” geometry.
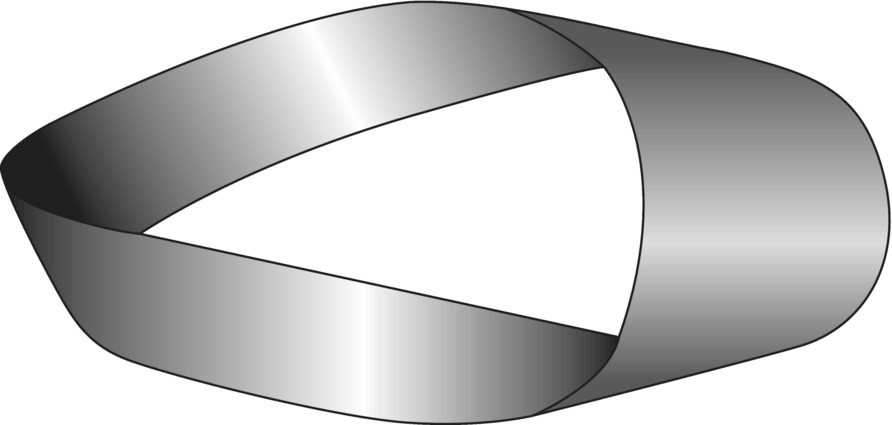
When we are told topology is concerned with properties of surfaces, curves, knots, and the intricacies of geometric objects, the first thing that comes to mind is what? Physical objects are so commonplace to our experience that it is hard to imagine anyone telling us something that is not familiar. That said, take a strip of paper and give one of the ends a half‐twist, then tape the ends together creating a loop. Now, take a second strip, but now give the ends a complete twist rather than a half‐twist. Now take a pencil and draw a line down the center of each of the two strips. Anyone not familiar with this simple experiment will be surprised with the result. The strip given a complete twist results in a simple loop as expected, but the strip given a half‐twist does not result in a loop at all, but a one‐sided surface called a ![]() strip. Now take a pair of scissors and cut the
strip. Now take a pair of scissors and cut the ![]() strip down the middle. Does your lifetime experiences with surfaces predict what happens? Are you left with two smaller
strip down the middle. Does your lifetime experiences with surfaces predict what happens? Are you left with two smaller ![]() strips? Or maybe you get one long two‐sided
strips? Or maybe you get one long two‐sided ![]() strip. Now try cutting the
strip. Now try cutting the ![]() strip, not down the middle of the strip, but one‐third the way from an edge. Do you know what happens now? Each time it is different. You can carry out your own experiments to find out if it is not intuitively clear.
strip, not down the middle of the strip, but one‐third the way from an edge. Do you know what happens now? Each time it is different. You can carry out your own experiments to find out if it is not intuitively clear.
While the ![]() strip is mesmerizing, probably its greatest impact has been to spur interest in topological concepts. Imagine if you can a surface made from rubber that can be stretched, bent, twisted, and deformed in any way one pleases, but just do not tear it. Although the shape can change in many ways, there are properties that remain unchanged. In plane geometry, one is concerned with distance, curvature, angle, and so on, but in topology one forgoes those more rigid geometric properties with the aim of discovering what one could argue are more fundamental properties of an object. Properties that remain unchanged under a continuous deformation are called topological properties, and we say two objects are topologically equivalent if each object can be stretched, bend or continuously deformed into the other. Like the iconic doughnut and coffee cup, they may not be geometrically equivalent in the sense of Euclid, but they are topologically equivalent in the sense of topology since with a little time and effort one can pull, stretch, kneed one into the other (see Figure 5.50).
strip is mesmerizing, probably its greatest impact has been to spur interest in topological concepts. Imagine if you can a surface made from rubber that can be stretched, bent, twisted, and deformed in any way one pleases, but just do not tear it. Although the shape can change in many ways, there are properties that remain unchanged. In plane geometry, one is concerned with distance, curvature, angle, and so on, but in topology one forgoes those more rigid geometric properties with the aim of discovering what one could argue are more fundamental properties of an object. Properties that remain unchanged under a continuous deformation are called topological properties, and we say two objects are topologically equivalent if each object can be stretched, bend or continuously deformed into the other. Like the iconic doughnut and coffee cup, they may not be geometrically equivalent in the sense of Euclid, but they are topologically equivalent in the sense of topology since with a little time and effort one can pull, stretch, kneed one into the other (see Figure 5.50).

Figure 5.50 The iconic doughnut and coffee cup equivalence.
We have often heard the story of the poor topologist who cannot distinguish a doughnut from a simple coffee cup, but the story is false and the joke is on everyone else. The topologist can tell the difference, it is just that the topologist does not care. Topology relaxes the rigid rules of geometry and seeks out new properties of objects remain invariant under more general transformations. The topologist discards the old geometric tools of ruler and protractor, replacing them with the new tool of continuity (see Figure 5.51).
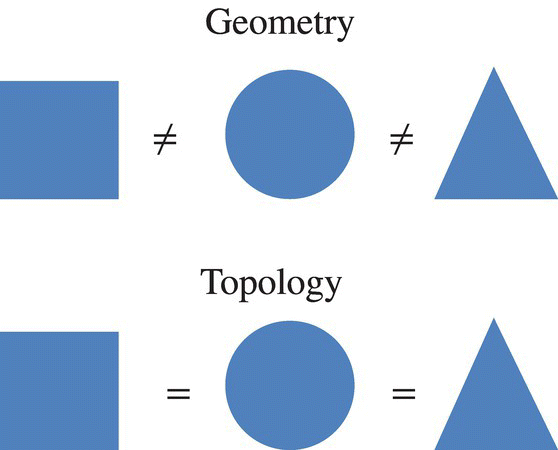
Figure 5.51 Topologically equivalent objects.
We go about our daily lives not giving much thought about many fundamental difference between objects. Look around you and think about some qualitative difference between objects. Figure 5.52 shows a few typical household objects with some fundamental differences between them that interest topologists.
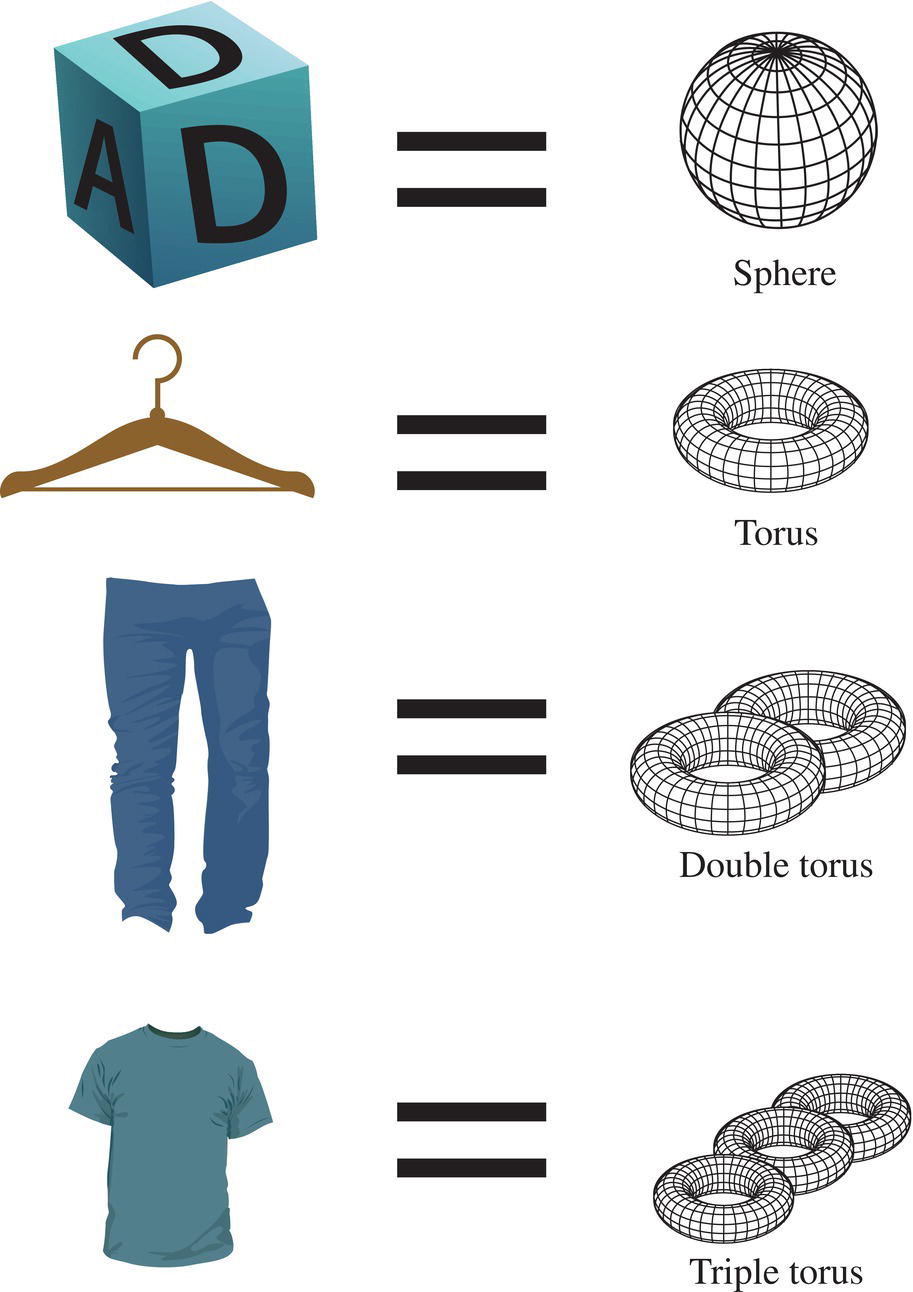
Figure 5.52 Household objects with topological similarities.
The previous discussion lead us to the formal definition of a homeomorphism and homeomorphic (or topologically equivalent) objects.
5.3.2 Topological Equivalent Objects
Table 5.2 Topologically homeomorphic letters.
| Topological invariants | Homeomorphic letters |
| no holes, no tails | {C, G, I, J, L, M, N, S, U, V, W, Z} |
| no holes, three tails | {E, F, T, Y} |
| no holes, four tails | {X} |
| one hole, no tails | {D,O} |
| one hole, one tail | {P,Q} |
| one hole, two tails | {A, R} |
| two holes, no tail | {B} |
| no holes, four tails | {H, K} |
Although many objects can be seen to be topologically equivalent visually, an analytic solution is preference if possible.
5.3.3 Homeomorphisms as Equivalence Relations
In Section 3.3, we saw that an equivalence relation partitions a set into equivalence classes, where the members of each equivalence class share a common property. We now show the relation of being homeomorphic between two sets is an equivalence relation, thus enabling one to partition surfaces, curves, and other objects into distinct equivalence classes whose members share a common property.
5.3.4 Topological Invariants
A major problem in geometric topology is to determine if two given objects are topologically equivalent. To show two objects are topologically equivalent it suffices to find just one homeomorphism between them. However, to prove that two objects are not homeomorphic, there is no special function that identifies nonhomeomorphic objects. To show that two objects are not homeomorphic, the strategy is to look at properties, called topological invariants, that are shared by homeomorphic objects. Thus, if two objects do not share a topological invariant, they are not homeomorphic.
One topological invariant of a surface is the property of being able to continuously shrink any simple closed curve on the surface to a single point on the surface. This is true for a sphere, but not true for a torus so we know the sphere is not topologically equivalent to a torus. (A string tied around the inside circle of a torus cannot be shrunk to a point.) (See Figure 5.53).

Figure 5.53 Topological test.
Other topological properties are the property of being connected (i.e. not the union of two disjoint pieces), the cardinality of a set, and the number of sides of a surface.
Table 5.3 lists a few topological properties for solid figures and surfaces. The reader may not be familiar with many of them, but should appreciate the fact that topologists have categorized dozens of such properties.
Table 5.3 A few topological properties.
| Topological properties of sets in the plane |
| Path‐wise connected |
| The number of path‐wise components |
| The number of cut points of similar types |
| Closed and bounded |
| Connectedness |
| Euler characteristic |
| Number of sides of a surface |
| A curve being simply connected |
5.3.5 Euler Characteristic for Graphs, Polyhedra, and Surfaces
We saw in Section 5.1 that a connected, planar graph with v vertices, e edges, and f faces satisfied the relation
called the Euler characteristic. It is not difficult to visualize that if the graph was drawn on a rubber sheet and no much you stretch or bend the rubber sheet, this number will always be two.
Although the Euler characteristic is valid for planar connected graphs in the plane, its importance is how it relates to polyhedra surfaces. A polyhedron is a solid whose surface consists of faces like squares, triangles, pentagons, and so on. Figure 5.44 shows the five famous polyhedra from Euclid's Elements, called the Platonic Solids. These solids, the tetrahedron, cube, octahedron, dodecahedron, and icosahedron, along with their planar graph representations, are drawn in Figure 5.54.

Figure 5.54 Platonic solids and their planar graph representations.
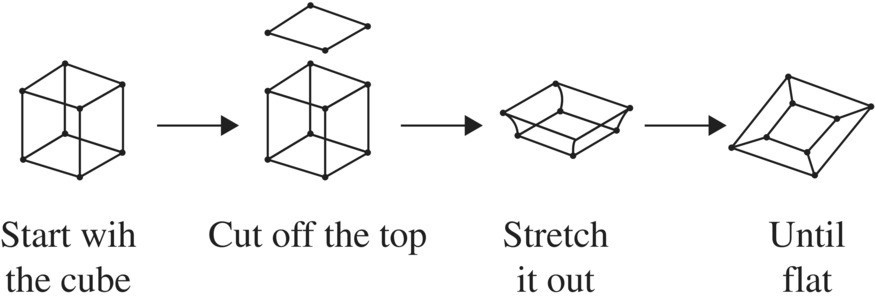
Figure 5.55 Converting a cube to its planar graph.
5.3.6 The Euler Characteristic of a Surface
The role of Euler's Characteristic in topology is that it helps determine if surfaces are topologically equivalent. If two surfaces do not have the same Euler characteristic, they are not topologically equivalent. For example the Euler characteristic of a sphere is two, while the Euler characteristic of a torus (doughnut) is zero, thus the sphere is not topologically equivalent to the torus. It is not hard to imagine that you cannot stretch and bend a sphere into the shape of a torus, or vice‐versa, no matter how hard you try.
Mathematicians find the Euler characteristic of a surface by a process of covering the surface with a net of polygons, often triangles consisting of vertices, edges, and faces. To explain how this is done, we demonstrate how a sphere can be “triangulated” with a series of vertices, edges, and faces in the form of a spherical tetrahedron.1 This surface tetrahedron suggests an inscribed tetrahedron as shown in Figure 5.56, and since the inscribed tetrahedron has Euler characteristic of two, and does not change as the tetrahedron is inflated to the shape of the sphere, we define the Euler characteristic of the sphere as that of the tetrahedron, which is two.

Figure 5.56 Finding the Euler characteristic of a sphere.
It is not necessary to use triangles for the net of polygons of the sphere. For example a net of squares leads to a topologically equivalent inscribed cube, which also having Euler characteristic of two and is unchanged as the cube is inflated to the shape of a sphere, thus defining the Euler characteristic of the sphere again as two (see Figure 5.57).
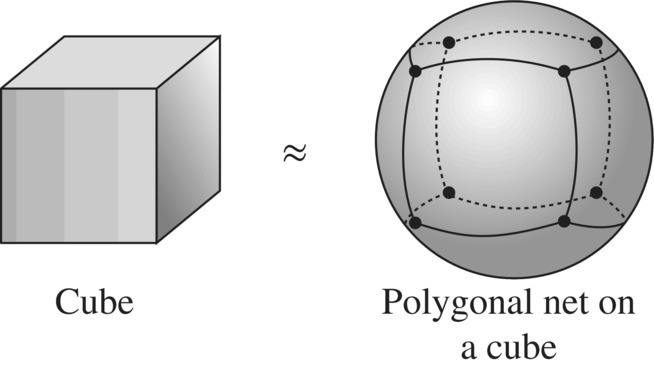
Figure 5.57 Finding the Euler characteristic of a sphere.
To find the Euler characteristic of the torus, we again construct a net of polygons that will inflate to that of the torus (see Figure 5.58).
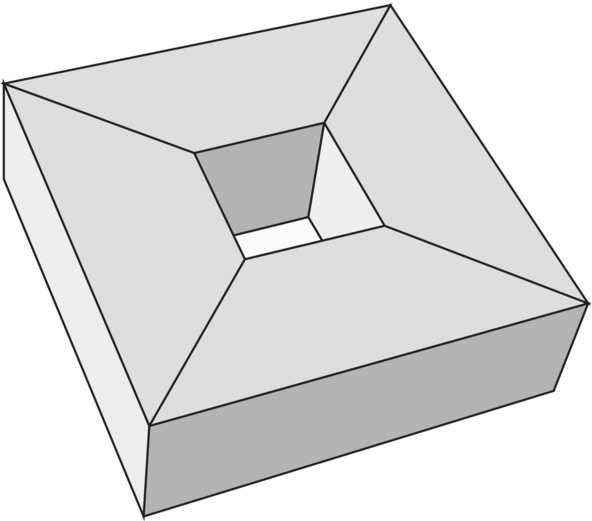
Figure 5.58 Polygon inscribed in a torus.
We now compute the Euler characteristic by carefully counting the vertices, edges, and faces of the (nonconvex) polygon in Figure 5.48. We cannot really see every side of the polygon in the drawing, but we can still imagine what is on the other side. Counting vertices, edges, and faces, we find the numbers given in Table 5.4:
Table 5.4 Euler characteristic of a torus.
| Top | Bottom | Vertical | Total | |
| Vertices | 8 | 8 | 0 | 16 |
| Edges | 12 | 12 | 8 | 32 |
| Faces | 4 | 4 | 8 | 16 |
Hence, we have the Euler characteristic of
Other types of surfaces like multihole tori containing multiple holes are not topologically equivalent to either the sphere or single‐hole torus. It turns out that each hole in a sphere decreases its Euler characteristic by two, thus a double‐hole torus has Euler characteristic of −2, a triple‐hole torus an Euler characteristic of −4, and so on.
Problems
- Experimenting with the Möbius Band
Take a piece of paper about a foot long and an inch wide. Bring the ends of the paper together and give the ends of the paper a half twist then tape the ends together. You have now created a Möbius strip drawn in Figure 5.59.2 You are now ready to carry out the following experiments.
- Take a red pencil and color one of the edges of the Möbius strip. Start anywhere on the strip and continue until you arrive back at the starting point. How many edges are there? Surprise, only one edge.
- Now let us color the sides of the strip. Draw a line down the middle of the strip until you arrive back at the starting point. How many sides are there to the strip? Double surprise.
- Things just get more curious with the Möbius strip. Now take a pair of scissors and cut the band lengthwise down the middle. What do you think will happen?
- Now create a second Möbius strip but this time instead of cutting the band down the middle, cut it about one‐third the way from one of the edges. The results now are even more surprising.
- The Doughnut and Coffee Cup
The doughnut and the coffee cup are two objects everyone knows are homeomorphic. Can you find other objects that are not homeomorphic to the doughnut or coffee cup? What are some topological properties of these objects that are different from those of the doughnut or coffee cut?
- Euler Characteristic Experiment
Start with a planar graph consisting of only one point and compute the Euler characteristic. Then start adding vertices and edges in any way you please. Note the Euler characteristic will always be 2.
- Euler Characteristic for Planar Polygons
Show that the Euler characteristic v − e + f of each of the polygons in the plane, square, polygon, hexagon, and octagon is one, although if you count the unbounded region outside the polygon as a face, then the Euler Characteristic is 2.
- Euler's Formula
Carry out the steps that Cauchy used to convert a polyhedron to a planar graph for a tetrahedron and an octahedron.
- Truncated Cube
A truncated solid is a polyhedra with its vertices clipped off drawn in Figure 5.60. Find the number of vertices, edges, and faces of the truncated cube and show that it has an Euler characteristic of two.
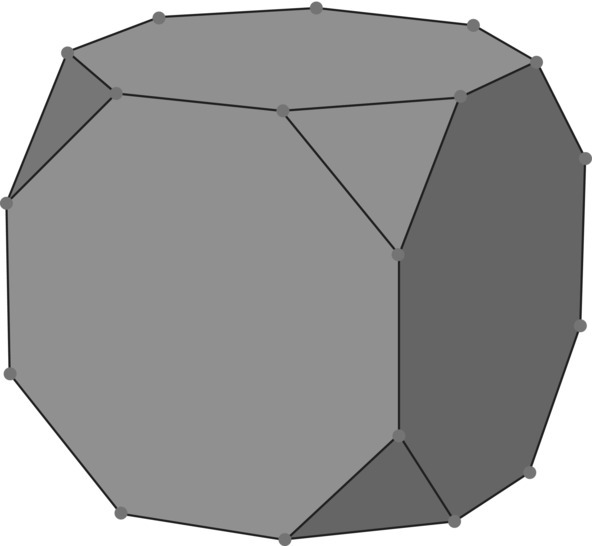
Figure 5.60 Truncated cube.
- Nonconvex Polyhedra
Euler's characteristic does not always have the value of two for nonconvex polyhedra. Show that the nonconvex polyhedra in Figure 5.61 has an Euler characteristic of 3.
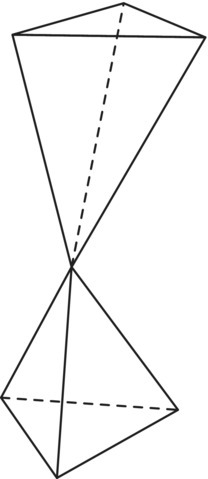
Figure 5.61 Nonconvex polyhedra.
- Toroidal Polyhedra
The (nonconvex) polyhedron drawn in Figure 5.62 called a toroidal polyhedra, which is topologically equivalent to the torus. Show that the Euler characteristic of this polyhedron is zero, thus defining the Euler characteristic for the torus.
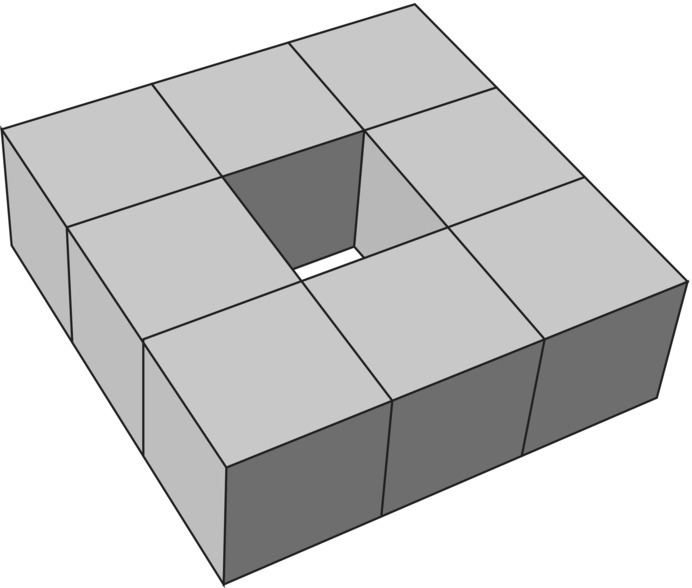
Figure 5.62 Toroidal polyhedra.
- Double Torus
The (nonconvex) polyhedra shown in Figure 5.63 is topologically equivalent to the double‐holed torus. Show that the Euler characteristic of this polyhedron is minus two, thus defining the Euler characteristic for the double‐holed torus.

Figure 5.63 Double‐holed torus.
- Triple‐Hole Torus
For each additional hole in the sphere, the Euler characteristic decreases by 2. Hence, the sphere has Euler characteristic 2, the single‐hole torus has Euler characteristic 0, the double‐hole torus −2, and the following triple‐hole torus −4. Show that the Euler characteristic of the triple‐hole torus drawn in Figure 5.64 is −4 Count carefully.

Figure 5.64 Triple‐hole torus.
- Internet Research
There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward Euler's characteristic of different surfaces, homeomorphisms, different topological properties, and visualizing topological equivalence.

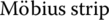 .
.