6.2
Introduction to the Algebraic Group
6.2.1 Basics of a Group
The idea of a symmetry is fundamental in science and its in‐depth study requires the mathematical machinery of the algebraic group. Group theory is one of the most useful mathematical tools for mathematicians and scientists alike, including particle physicists, where group theory is the language for understanding the structure of particle physics.
The most fundamental component of a group is its binary operation.
6.2.2 Binary Operations and the Group
A binary operation on a set A is a rule, which assigns to each pair of elements of A a unique element of A. Thus, a binary operation is a function f : A × A → A. Two common binary operations familiar to the reader are +, × which assign the sum a + b ∈ ℝ and product a × b ∈ ℝ to a pair (a, b) ∈ ℝ × ℝ of real numbers. We now give a formal definition of a group.
Often, it happens that a * b = b * a for all a, b ∈ G. When this happens, the group is called a commutative (or Abelian) group. We also denote the group operation a * b simply as ab, or maybe by ⊕ if the group operation is addition or resembles addition. A group is called finite if it contains a finite number of elements and the number of elements in the group is called the order of the group. If the order of a group G is n, we denote this by writing |G| = n. If the group is not of finite order, we say it is of infinite order.
Table 6.3 shows some binary operations of different sets.
Table 6.3 Properties of binary operations.
| Properties of binary operations | ||||
| Operation | Associative | Commutative | Identity | Inverse |
| ∪ on P(A) | Yes | Yes | Yes | No |
| ∩ on P(A) | Yes | Yes | Yes | No |
| gcd on ℕ | Yes | Yes | No | No |
| + on ℝ | Yes | Yes | Yes | Yes |
| − on ℝ | No | No | No | No |
| × on ℚ | Yes | Yes | Yes | Yes |
| min on ℝ | Yes | Yes | No | No |
6.2.3 Cayley Table
The binary operation of a finite group can sometimes be illustrated by means of a Cayley table as drawn in Figure 6.16, which shows the products gigj of two members gi and gj of the group. It is much like the addition or multiplication tables the reader studied as a child. A Cayley table is an example of a Latin square, meaning that every element of the group occurs once and exactly once in every row and column. We examine the Cayley table to learn about the inner workings of a group.

Figure 6.16 Cayley table for a group.

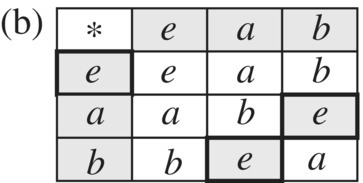
Figure 6.17 (a) Order 2. (b) Order 3.
The graphs demonstrated in Figure 2 are the only graphs of order 2 and 3, respectively. For order 4 however, there are two possible groups, one is the Klein four‐group and the other the cyclic group of order 4. The group in Example 3 is the cyclic group of order 4. The Klein four‐group will come later.

Figure 6.18 Order 4 group.
In general, there is no quick way to verify the associative property like there is for the commutative property. One must check all possible arrangements to verify the property. On the other hand, if one instance where the associative property fails, then the binary operation * is not associative.
Example 3 illustrates one of the two groups of order 4. We now present the other group of order 4, the Klein four‐group.
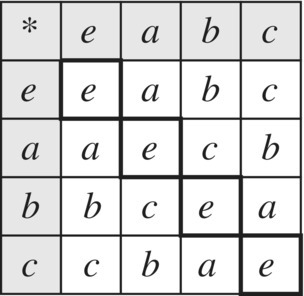
Figure 6.19 Klein four‐group.
Table 6.4 Common groups.
| Group | Elements | Operation | Identity | Inverse |
| ℤ | n ∈ ℤ | Addition | 0 | −n |
| ℚ + | Multiplication | 1 | n/m | |
| ℤn | k ∈ {0, 1, 2, … , n − 1} | Addition mod n | 0 | n − k |
| ℝ − {0} | x nonzero real number | Multiplication | 1 | 1/x |
| ℝ2 | (a, b) ∈ ℝ2 | Vector addition | (0, 0) | (−a, − b) |
6.2.4 Cyclic Groups: Modular Arithmetic
The most common and most simple of all groups are the cyclic groups, which are well‐known to every child who has learned to keep time.
For example, the three rotational symmetries {e, R120, R240} of an equilateral triangle form a cyclic group ℤ3 with generator g = R120 since ![]() .
.
Cyclic groups also describe modular (or clock) arithmetic, which is the arithmetic we perform when keeping time on 12‐hour clock. The 12‐hour clock leads us to the cyclic group Z12 with elements
and group operation
which is basically the arithmetic you do when keeping time. The “mod 12” simply refers to computing a ⊕ b by computing the ordinary sum (a + b), then taking its remainder after dividing by 12. We denote the group operation by ⊕ to remind us that the operation is addition, only reduced modulo 12. In clock arithmetic, the equation 2 = (9 + 5) mod 12, which can be interpreted as meaning five hours after 9 p.m. is 2 a.m.
The 12 hours of the clock, 0 through 11, along with the binary operation of addition modulo 12 is an Abelian group of order 12 called the cyclic group of order 12, denoted by (ℤ12, ⊕). The Cayley table for this group is shown in Figure 6.20.

Figure 6.20 Cayley table for the cyclic group of 12 elements.
Figure 6.21 shows various clocks that give rise to different cyclic groups.
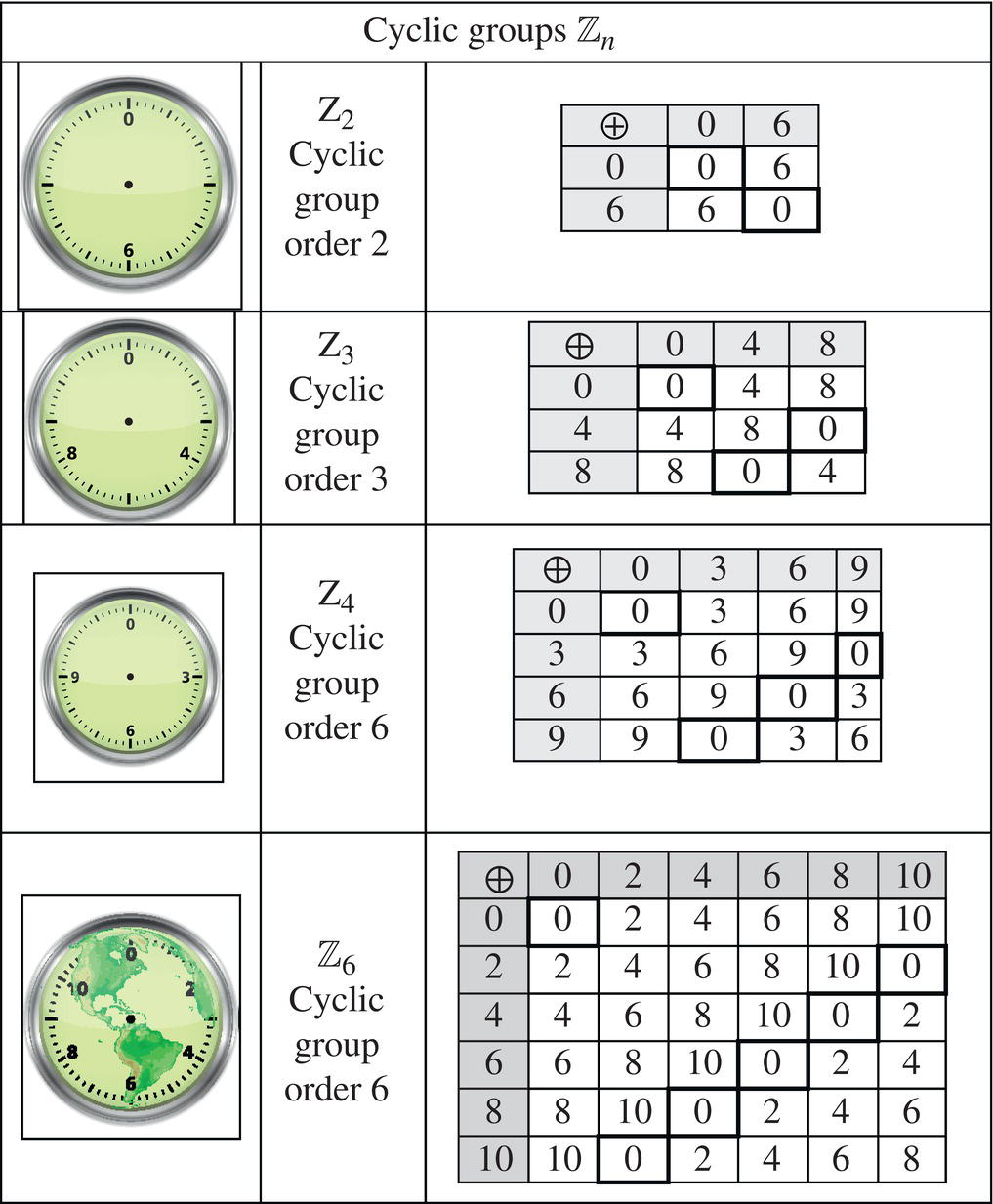
Figure 6.21 Finite cyclic groups.
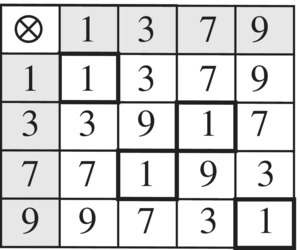
Figure 6.22 Cayley table for U(10).
Note that the group is Abelian and that 3−1 = 7, 7−1 = 3 since 3 × 7 = 1.
6.2.5 Isomorphic Groups: Groups that are the Same
Sometimes groups appear different when looking at their Cayley tables, but after relabeling their elements, one discovers they are the same group. For example, consider two groups illustrated in Figure 6.23.

Figure 6.23 Isomorphic groups.
The group at the left is the cyclic group ℤ4 = {0, 1, 2, 3} and the group at the right consists of the four numbers G = {1, i, − 1, − i} which lie on the unit circle in the complex plane, where the group operation is multiplication (see Figure 6.24).

Figure 6.24 Isomorphism.
Looking carefully at the two Cayley tables in Table 6.4, you will see that the numbers 0, 1, 2, 3 in the table for ℤ4 are arranged in the same order as the numbers 1, i, − 1, − i in the table for G. If we make the correspondences
we see that the groups ℤ4 and G are the same, they simply use different symbols. When two groups are the same, but only different in their symbols used in their description, the groups are called isomorphic. In this example, the described one‐to‐one correspondence is called an isomorphism between the groups. This motivates the following formal definition of an isomorphism.
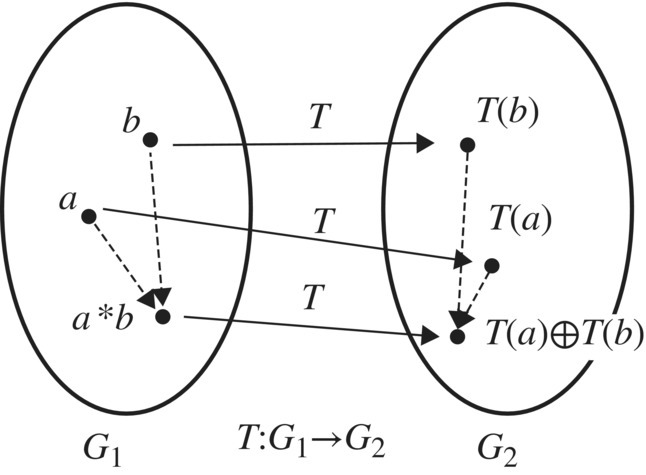
Figure 6.25 Isomorphism.
Roughly speaking, for isomorphic groups, the mapping and the group operations can be carried out in either order. You can operate then map T(a * b), or you can map and then operate, T(a) ⊕ T(b), the results are the same.
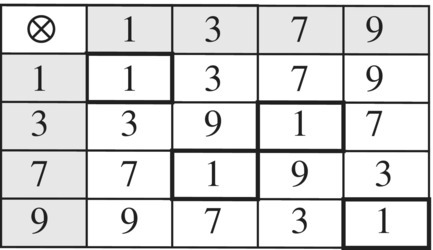
Figure 6.26 Relative prime group.
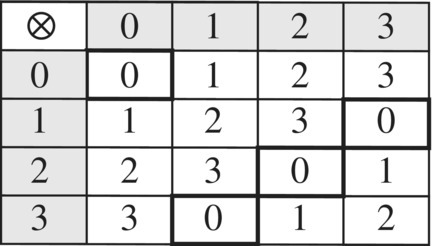
Figure 6.27 Cyclic group of order 4.
6.2.6 Dihedral Groups: Symmetries of Regular Polygons
In Section 6.1, we saw how the symmetries of a figure form an arithmetic system where one can “multiply” symmetries much like we multiply numbers. The set of symmetries of an object along with the arithmetic operation of composition of symmetries forms a group of symmetries for the figure. Every figure, no matter how “nonsymmetric,” has one symmetric group, the trivial symmetry, however, the more symmetric a figure, the larger its symmetry group. A rectangle has four symmetries, whereas the more “symmetrical” square has eight symmetries. Can you find them?
A polygon is called regular if all its sides have the same length and all its interior angles are equal. An equilateral triangle is a regular 3‐gon, a square is a regular 4‐gon, a pentagon a regular 5‐gon, and so on. The symmetry group of a regular n‐gon has n rotational symmetries and n flip symmetries for a total of 2n symmetries. This group is called the dihedral group of the n‐gon and denoted by Dn Can you find the 10 symmetries of the dihedral group D5 of the pentagon drawn in Figure 6.28?
Figure 6.28 Find the symmetric group D5.
6.2.7 Multiplying Groups
There are only two (nonisomorphic) groups of order 6, the dihedral group D3 and the cyclic group ℤ6. Sometimes groups can be factored into smaller groups somewhat like the number six that can be factored as 6 = 3 × 2. The cyclic group ℤ6 can be factored as the Cartesian product
of the two smaller cyclic groups ℤ3 and ℤ2 where if we define the group operation on the Cartesian product as
we arrive at the Cayley table in Figure 6.29.

Figure 6.29 ℤ3 × ℤ2.
Also, if we make the following identification
the multiplication table in Figure 6.29 is the multiplication table for the cyclic group ℤ6, as shown in Figure 6.30.

Figure 6.30 Multiplication table for ℤ6.
Problems
- Groups?
Do the following sets with given binary operations to form a group? If they do, find the identity element and the inverse of each element. If it does not form a group, explain why not.
- even integers, addition
- {−1, 1 }, multiplication
- nonzero complex numbers, multiplication
- nonzero rational numbers, multiplication
- positive rational numbers, multiplication
- complex numbers 1, − 1, i, − i, multiplication
- positive irrational numbers together with 1, multiplication
- integers, subtraction.
- Odd Integers Under Addition
Give reasons why the odd integers under addition do not form a group?
- Finish the Group
Complete the following Cayley table in Figure 6.31 for a group of order 3.
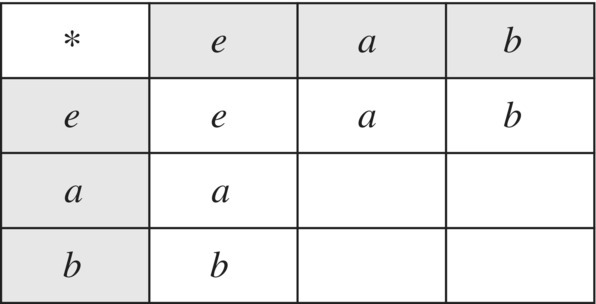
Figure 6.31 Order 3 Cayley table.
- Finish the Group
Complete the following Cayley table in Figure 6.32 for a group of order 4 without looking at the Cayley tables of the Klein four‐group or the cyclic group of order 4 in the text.
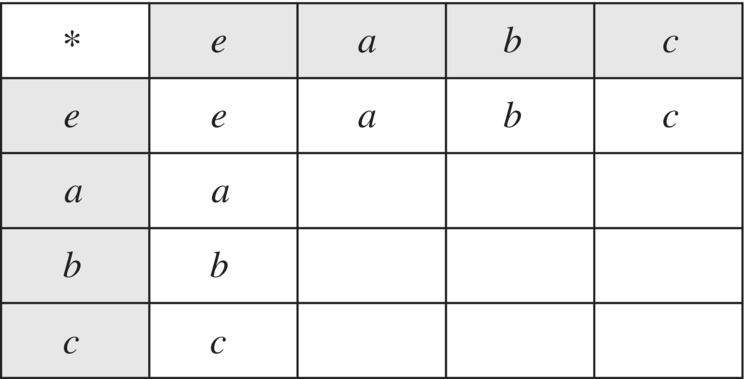
Figure 6.32 Klein four‐group.
- Verification of a Group
Do the nonzero integers with the operation of multiplication form a group?
- Group You are Well Familiar
Show {ℤ, +} is a group.
- Property of a Group
Verify that for all elements a, b in a group, the following identity holds.
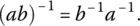
Hint: Show (ab)(b−1a−1) = e.
- Heisenberg Group
A group that plays an important role in quantum mechanics is the Heisenberg group which consists of all matrices of the form

where x, y, z are real numbers, and the group operation is matrix multiplication. Show that this is a group.
- Direct Product of Groups
Define a group (ℤ2 × ℤ2, ⊕) consisting of the Cartesian product
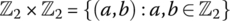
and binary operation

Find the Cayley table for this group.
- Modulo 5 Multiplication
Create the multiplication table for the integers 1, 2, 3, and 4, where multiplication is defined as mod(5) arithmetic.
- Modulo 4 Multiplication
Create the multiplication table for the integers 1, 2, and 3 for modular arithmetic mod(4) and show that this does not define a group. In other that the numbers 1, 2, … , n − 1 forms a group under mod(n) multiplication, it must be true that n is a prime number.
- Relative Prime Group U(10)
For each positive integer n, the set of positive integers 1, 2, …, n that are relatively prime6 with n is denoted by U(n). For example, U(10) = {1, 3, 7, 9}. The set U(n) is a group under multiplication modulo n.
- Draw the Cayley table for U(10).
- Is the group Abelian?
- What is the inverse of each element?
- Relative Prime Group U(8)
For each positive integer n, the set of positive integers 1, 2, …, n that are relatively prime with n is denoted by U(n). For example U(8) = {1, 3, 5, 7}. The set U(n) is a group under multiplication modulo n.
- Draw the Cayley table for U(8).
- Is the group Abelian?
- What is the inverse of each element?
- Isomorphic Groups
Show that the following Group C and Group D in Figure 6.33 are isomorphic by interchanging the third and fourth columns of C, and then the third and fourth rows to get the table for D.
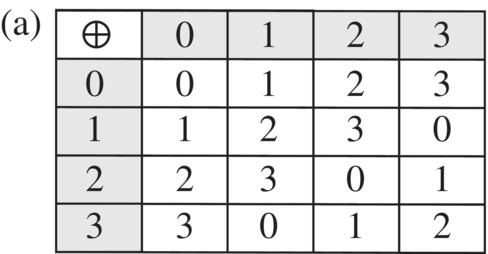

Figure 6.33 (a) Group C. (b) Group D.
- Infinite Group
Show that the set of all rational numbers x in the interval [0, 1) form an infinite group if the group operation is defined as
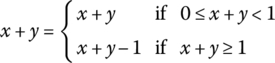
- Groups and Latin Squares
The Cayley table for a group forms what is called a Latin square. That is, every element of the group occurs exactly once in every row and exactly once in every column. The converse is not true, however, since there are Latin squares that do not form groups. Find a Latin square for the numbers {0, 1, 2} that does not form a group.
- Modular Fun
Compute the following sums and products in the given cyclic group ℤn = {0, 1, 2, … , n − 1}.
- ℤ4 : 1 + 7 and 3 × 7
- ℤ5 : 9 + 7 and 5 × 7
- ℤ6 : 10 + 7 and 2 × 7
- ℤ9 : 11 + 20 and 3 × 7
- ℤ10 : 100 + 7 and 30 × 10
- ℤ11 : 11 + 11 and 11 × 7
- ℤ11 : 12 + 7 and 10 × 10
- ℤ15 : 14 + 1 and 3 × 6
- Group

If a, b are rational numbers, not both zero, then show the set
 forms a group under multiplication
forms a group under multiplication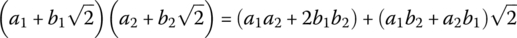
- Verification of a Group
Prove that the nonzero real numbers ℝ* = ℝ − {0} with binary operation * is a group, where
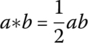
- Homomorphisms
The most important functions between two groups are homomorphisms, those that “preserve” the group operations. More precisely, a function f : G → H between two groups is a homomorphism when
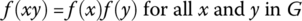
where xy denotes the group operation in G and f(x)f(y) denotes the group operation in H. The following identities describe homomorphisms between two groups, where group operations are understood. What are the groups G, H, and what is the homomorphism between the groups?
- c(x + y) = cx + cy
- |xy| = |x||y|
- (xy)2 = x2y2
- loga (xy) = logax + logay
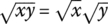
- Internet Research
There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward applications of group theory, history of group theory, and examples of groups of different sizes.
