6.3
Permutation Groups
6.3.1 Permutations and Their Products
In Section 2.3, we introduced the concept of a permutation (or arrangement) of a set of objects. We now return to the subject, but now our focus is different. Instead of thinking of a permutation as an arrangement of objects (which it is, of course), we think of a permutation as a one‐to‐one correspondence (bijection) from a set onto itself. For example, a permutation of elements of the set A = {1, 2, 3, … , n} can be thought of a one‐to‐one mapping of the set onto itself, represented by
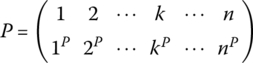
which gives the image kp of each element k ∈ A in the first row as the element directly below it in the second row.
For example, a typical permutation of the four elements A = {1, 2, 3, 4} is

A good way to think about this permutation is to think of a tomato, strawberry, lemon, and apple, arranged from left to right in positions we call 1, 2, 3, and 4. If we apply the permutation P mapping, we get the new arrangement shown in Figure 6.34.

Figure 6.34 Permutation mapping.
The tomato that was originally in position 1 has moved to position 2, the strawberry that was in position 2 has moved to position 3, and so on. The important thing to know is that although the individual items have moved, the positions 1, 2, 3, and 4 remain the same.
Another way to think of a permutation is with a directed graph, as drawn in Figure 6.35. Here, we see the movement of the fruits as everything is shifted to the right, and the apple at the end goes to the front of the line. Again, think of the fruits as moving, but the positions are fixed.
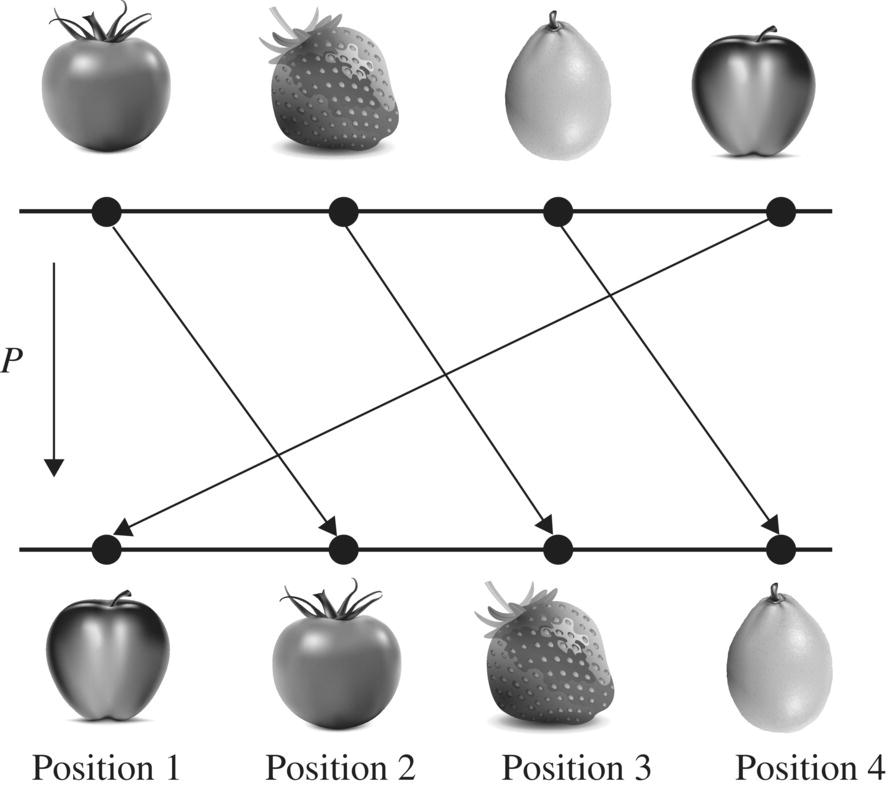
Figure 6.35 Visualization of a permutation.
6.3.1.1 Product of Permutations
Starting with the permutation:
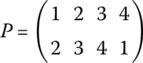
suppose we follow this permutation by a second permutation Q. In other words, the composition of the permutation P is followed by a second permutation Q, which gives rise to a “reshuffling of a reshuffling.” This leads us to the definition of the product of two permutations.
The product of the permutations P and Q is shown in Figure 6.36.

Figure 6.36 Permutation product.
Figure 6.37 illustrates the movement of the four fruits under the action of this product.
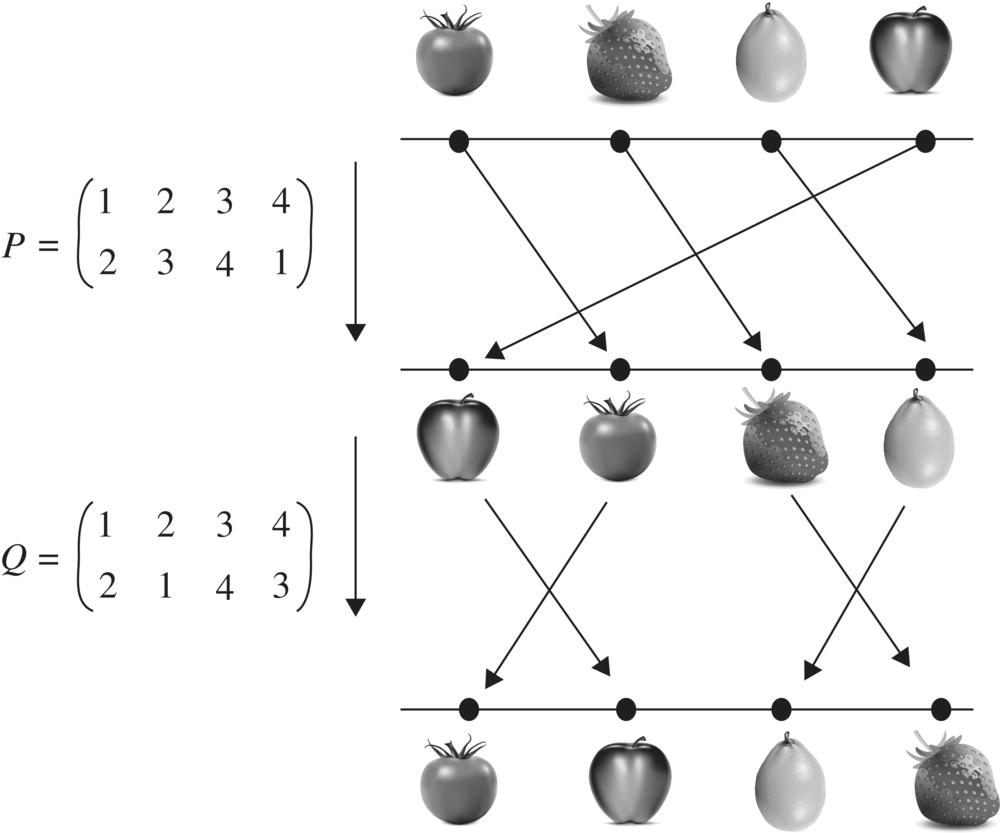
Figure 6.37 Product (composition) of two permutations.
A second visualization of this permutation product is shown in Figure 6.38. This time we use Greek symbols.
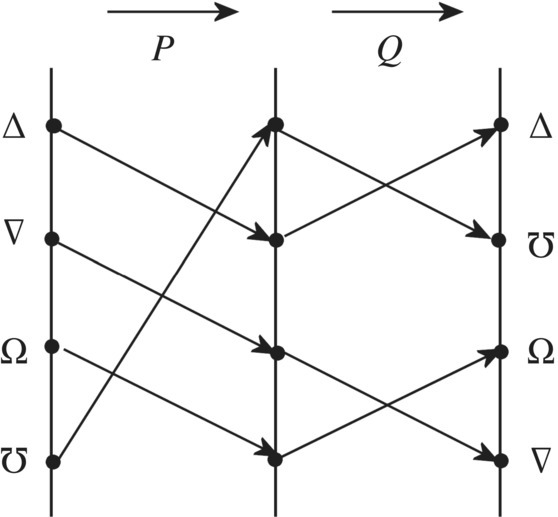
Figure 6.38 Another representation of the product of permutations.
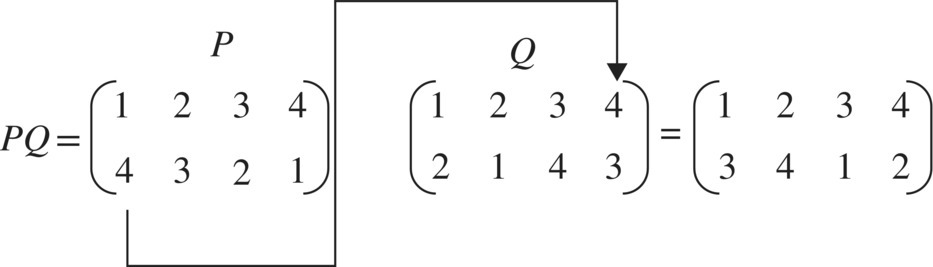
Figure 6.39 Product of permutations.
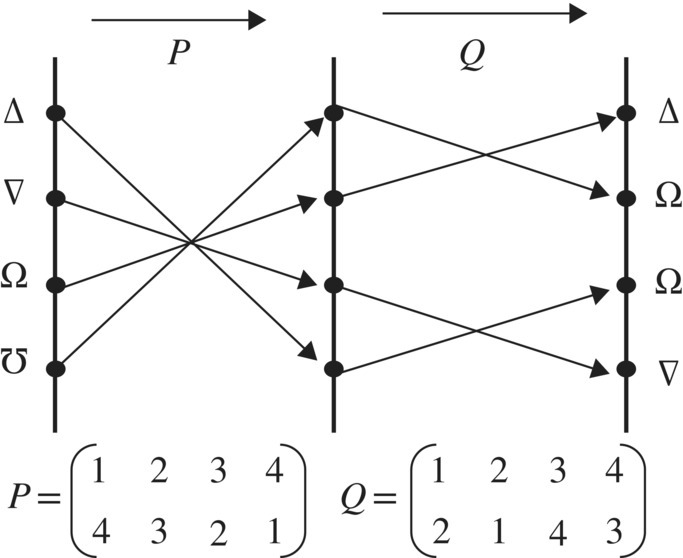
Figure 6.40 Composition of two permutations.
6.3.2 Inverses of Permutations
If a permutation P maps k to kP, then its inverse P−1 maps kP back onto k. In other words, the inverse of a permutation can be found by simply interchanging the top and bottom rows of the permutation P. For convenience in reading however, we reorder the top row 1, 2, n from left to right. For example
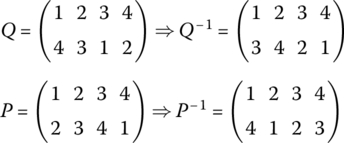
The reader can verify that
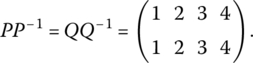
6.3.3 Cycle Notation for Permutations
A more streamlined way to display permutations is by the use of the Cauchy cycle (or cyclic) notation. To illustrate how this works, consider the permutation2

To write this permutation in cyclic notation, we start at the upper left‐hand corner with 1 and write (1 and then follow it with its image 1P = 3, that is (13. Next, note that P maps 3–5, so we write (135. Then P maps 5 back to the original 1, so we have our first cycle (135). We then continue on with 2 (next unused element in the first row) and observe that P maps 2 to itself, so we have a 1‐cycle (2). Finally, we see that P maps 4–6, so we write (46 and since 6 maps back to 4 we have our final cycle, the 2‐cycle (46). Hence, P is written in what is called the product of three cycles: a 3‐cycle, a 1‐cycle, and a 2‐cycle,
where we dropped the 1‐cycle (2) to streamline the notation.
6.3.4 Products of Permutations in Cycle Notation
When computing the product of permutations expressed in cycle notation, one reads from left to right and thinks of each cycle as a function and the entire product as the composition of functions.3 The process is best explained with an example. Consider the product of four cycles
Starting with 1 in the left‐most cycle, we see it maps to 4, whereupon we move to the second cycle that does not contain 4, so we move to the third cycle that maps 4–2, whereupon we move to the last cycle that does not contain a 2, so we conclude that the product 1 maps to 2, whereupon we start the product permutation as (12…). We then carry out the same process starting at the leftmost permutation to find the image of 2, whereupon the first cycle does not contain 2 so we move to the second cycle and see that 2 maps to 3, and since none of the remaining cycles contain 3, we conclude the product maps 2 maps to 3, so we write the product as (123…). Continuing this process, we obtain the final product of (1234).
Using the directed graph in Figure 6.41 as a guide, see if you are able to carry out the multiplication (1532)(35)(14) of these cycle permutations. Think of someone giving three commands one after the other to a group of five people standing in a row, then ask yourself where will each of the people end up. Think of following each person moving from position to position at each command. We see the person starting in location “1” moves to position “5” on the first command, then to position “3” on the second command, and stays at position “3”on the third command.

Figure 6.41 Product of cycles.
6.3.5 Transpositions
A permutation that interchanges just two elements of a set and leaves all others unchanged is called a transposition (or 2‐cycle). For example
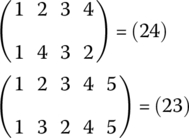
are transpositions. What may not be obvious is that any permutation can be written as the product of transpositions. In other words, any permutation of elements can be carried out by repeated interchanges of just two elements. For example Figure 6.42 shows four girls lined up from left to right waiting to get their picture taken. The photographer asks the three on the left to move one place to their right, and the end girl to move to the left position, which is a result of the following permutation.

Figure 6.42 Rotation permutation.
The question then arises, is it possible to carry out this maneuver by repeated interchanges of members, two at a time? The answer is yes, and the equation is
To see how this works, watch how they move in Figure 6.43.
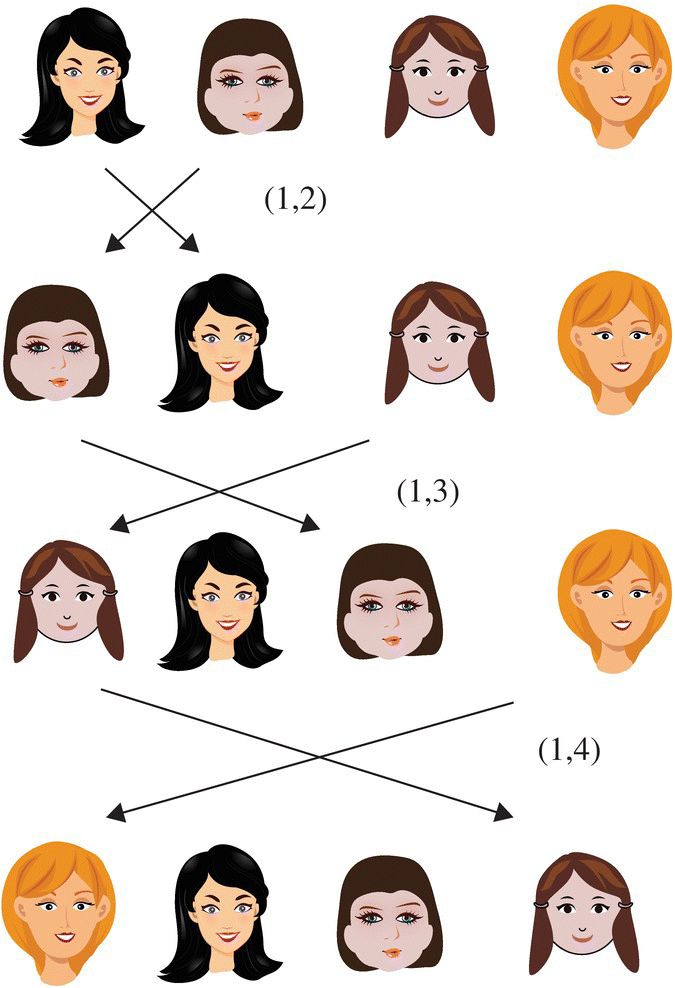
Figure 6.43 Permutation as a product of transpositions.
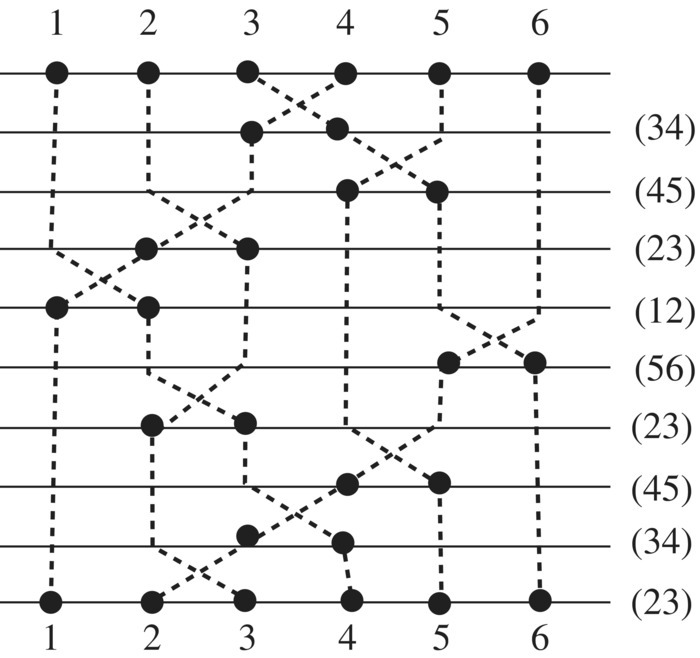
Figure 6.44 Permutation as the product of transpositions.
6.3.6 Symmetric Group Sn
We now show that the set of all permutations of a set forms a group.
6.3.7 Symmetric Group S3
In Section 6.2, we constructed the group of rotational and reflective symmetries of an equilateral triangle called the dihedral group D3. What we did not realize at the time was that this dihedral group of symmetries is the same as the symmetric group S3 of all permutations of the three vertices {1, 2, 3} of a triangle. Figure 6.45 illustrates this relationship.

Figure 6.45 Abstract equivalence of S3 and D3.
The Cayley table for the group symmetric group S3 is shown in Figure 6.46.
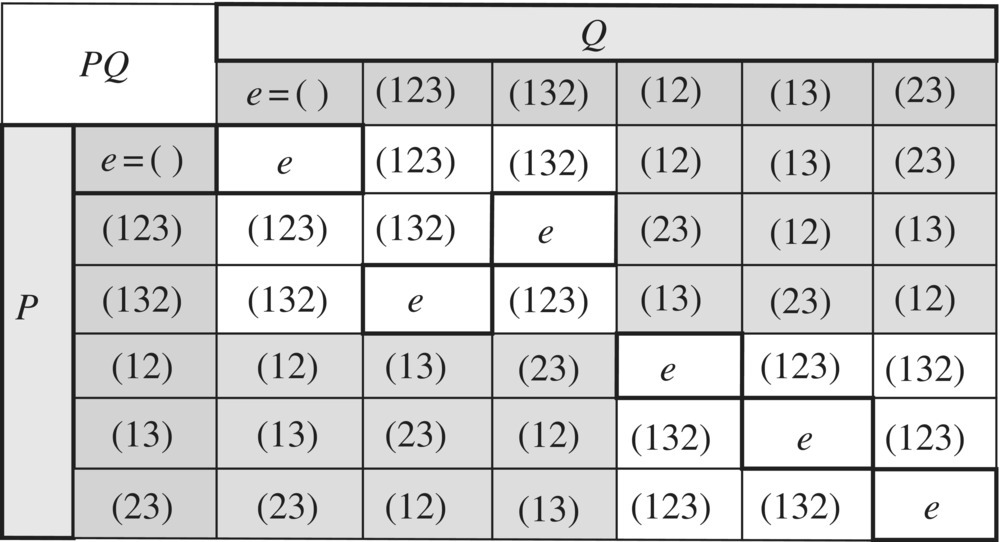
Figure 6.46 Symmetric group S3.
6.3.8 Alternating Group
From the Cayley table of S3 drawn in Figure 6.46, there is an obvious subgroup located at the upper left of the table in the unshaded region called the alternating group A3 with members
The property that characterizes this subgroup may not be obvious at first glance, but when its members are expressed in terms of fundamental transpositions, they all have an even number as seen by

whereas the other three permutations of S3, namely (12), (13), (23) have an odd number of transpositions (namely one). It is a general property of the symmetric group Sn that half the n! permutations have an even number of transpositions, called the even permutations, and half the permutations have an odd number of transpositions, called the odd permutations. The even permutations (which always contain the identity permutation) form an alternating subgroup An of order n !/2. Many of these alternating groups have interesting properties. The alternating group A4 of the 12 even permutations of S4 are the symmetries of the regular tetrahedron.
Problems
- Finding Permutations
Given the permutations
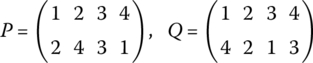
find:
- PQ
- P−1
- QP−1
- P2
- (PQ)−1
- Permutation Identity
For permutations

prove or disprove (PQ)−1 = Q−1P−1.
- Cycle Notation
Fill in the blanks in the permutation
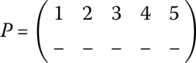
represented by the following cyclic products.
- (13)(24)
- (123)(45)
- (1432)
- (1)(2)(35)(4)
- (135)(42)
- Composition of Permutations
Given the permutations:
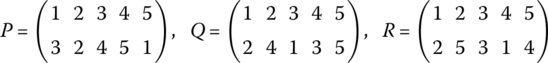
- Show that PQ ≠ QP
- Verify (PQ)R = P(QR)
- Verify (PQ)−1 = Q−1P−1
- Cycles as the Product of Two‐Cycles
A two‐cycle is an exchange of two elements of a set, such as the permutation (23) of interchanging 2 and 3, leaving the other elements of the set unchanged. Every permutation of a finite set can be written (not uniquely) as the product of two‐cycles. Write the permutation (12345) as the product or composition of two‐cycles. Take five different objects and put them in a row and verify that your answer is correct by shuffling them in both ways.
- Symmetric Group S2
Given the set A = {1, 2}.
- Construct the Cayley table for the group of permutations on A.
- What is the order of this group?
- Is the group Abelian?
- What is the inverse of each element of the group?
- Transpositions
Verify the following products.
- (1234 … n) = (12)(13)(14)⋯(1n)
- (214) = (21)(24) = (24)(41)
- (4321) = (43)(42)(41)
- (15324) = (15)(13)(12)(14)
- Do Transpositions Commute?
Do transpositions commute in general? For the set {1, 2, 3}, is it true that (12)(13) = (13)(12)?
- Decomposition into Transitions Is Not Unique
Show that the decomposition of the permutation (12345) can be written in any of the three forms:
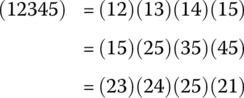
Cartesian (or Direct) Product of Groups
It is possible to piece together smaller groups to form larger groups. If H and G are groups, their Cartesian product4 is
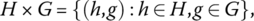
where the group operation * in H × G is
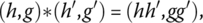
where hh′ is the group operation in group H, and gg′ is the group operation in group G. The following problems illustrate some Cartesian products of groups.
- Cartesian Product ℤ2 × ℤ2
Consider the cyclic groups ℤ2 = {0, 1},where the group operation is addition mod 2. Find the Cartesian product ℤ2 × ℤ2 and construct its multiplication table. Show the table is the same as the multiplication table for the Klein four group of symmetries of a rectangle. In other words, the Klein four group is isomorphic to ℤ2 × ℤ2.
- Cartesian Product Group ℤ2 × ℤ3
Find the elements of the Cartesian product ℤ2 × ℤ3. What is the order of the group? What is the Cayley table for the group? Hint: Keep in mind that the product (a, b)(c, d) = (e, f), where e = (a + c) mod 2, f = (b + d) mod 3.
- Permutation Matrices
The permutation

can be carried out with a 3 × 3 matrix.
- Find the matrix?
- Find the six matrices that represent the six permutations of S3.
- Internet Research
There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward permutations in cycle notation, symmetric group, permutation group, and puzzles with permutations.
