6.5
Rings and Fields
6.5.1 Introduction to Rings
Although the algebraic group has one binary operation, the algebraic system we studied in grade school has two binary operations: addition and multiplication. This leads us to the study of rings and fields. We begin with one of the most important abstract systems with two binary operations called a ring.1 A ring is one of the basic structures of abstract algebra, which generalizes the common arithmetic operations of the integers, polynomials, matrices, and so on. Ring theory is used today to understand basic physical laws, such as those underlying such things as symmetry phenomena in molecular chemistry.
You have seen examples of rings before. The integers ℤ with ordinary addition (+) and multiplication (×) are an example of an algebraic ring. In this regard, you might think of a ring as “generalized integers.” The study of rings was initiated (in part) by the German mathematician Richard Dedekind (1831–1916) in the late 1800s, and the axiomatic foundations were laid down in the 1920s, and most of them by the German mathematician Emmy Noether.
The first thing one notes about a ring is that practically no conditions are imposed on the multiplication, only that it is associative and obeys distributive laws. The action in a ring lies with the addition.
We denote the ring operation of addition by + and multiplication by ×, although they do not necessarily denote addition and multiplication of numbers. We often denote ring multiplication by ab for shorthand. We also call the additive identity in the ring, the zero (or additive identity) of the ring, and denote it by 0. A ring need not have a multiplicative identity, but when it does, we say the ring has a multiplicative identity (or unity) and is denoted by, you guessed it, 1.
6.5.2 Common Rings
- Example 1 The integers ℤ = {0, ± 1, ± 2, …} with usual addition and multiplication are a commutative ring with the multiplicative identity of 1.
- Example 2 The set ℤ[x] of all polynomials in x with integer coefficients and usual addition and multiplication is a commutative ring with multiplicative identity f(x) = 1.
- Example 3 The set 2ℤ = {0, ± 2, ± 4, …} of even integers with usual addition and multiplication is a commutative ring without a multiplicative identity.
- Example 4 The set ℤn = {0, 1, 2, … , n − 1} with addition and multiplication modulo n is a commutative ring with multiplicative identity 1. This ring is called the ring of integers modulo n.
- Example 5 The set M2(ℤ) of all 2 × 2 matrices with integer entries is a noncommutative ring with multiplicative identity

- Example 6 The sets ℤ, ℚ, ℝ with the usual addition and multiplication are all rings. The additive identity in each of these rings is 0 and the multiplicative identity is 1.
- Example 7 An important ring is the set of polynomials of the form
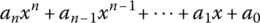
for a given natural number n and real coefficients with normal addition and multiplication of polynomials. Note that addition, subtraction, and multiplication are closed operations, but division is not.
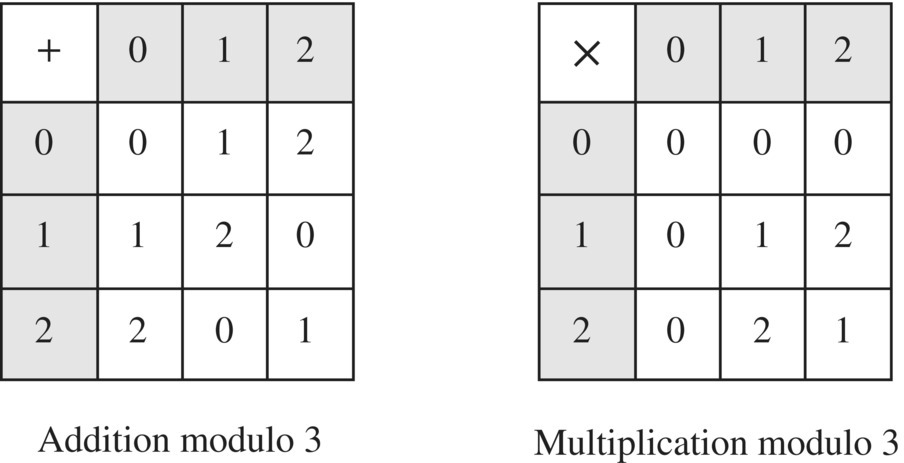
Figure 6.56 Special ring.
Note that the addition table forms a commutative group, and if we only look at the nonzero members {1, 2} of the multiplication table, they form a commutative group of order two. This is special kind of ring called a field. But not all rings have this much structure, as the following example illustrates.
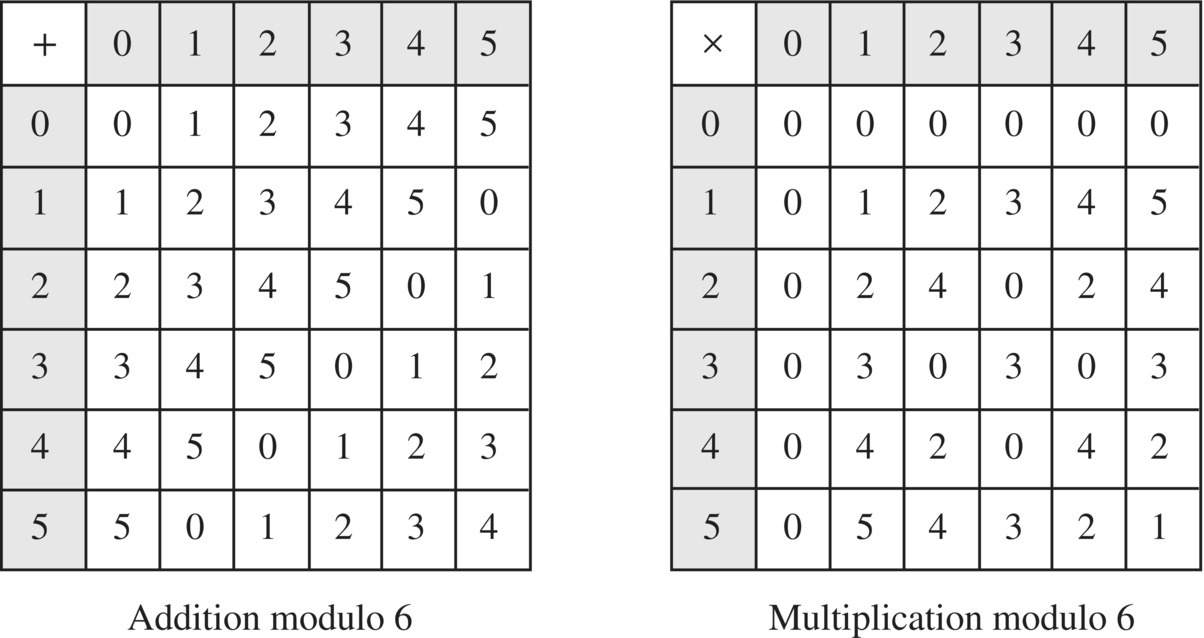
Figure 6.57 Cyclic ring.
Although the addition table for ℤ6 forms a commutative group with additive identity 0, the nonzero members of the multiplication table do not form a group for a variety of reasons. First off, the numbers 2, 3, and 4 do not have multiplicative inverses since there is no member of the ring that satisfies the equations 2 × a = 1, 3 × a = 1, 4 × a = 1.
Although rings are important algebraic structures in many areas of mathematics,2 they sometimes are too restrictive. For example, in the ring of integers ℤ under ordinary addition and multiplication, we cannot divide 3 by 5 to obtain a member of the ring. This leads us to the study of the algebraic field.3
6.5.3 Algebraic Fields
Rings allow for addition, subtraction, and multiplication, but not division. The equation 3x = 7 has no solution in the ring of integers but does have a solution in the field of rational numbers. An algebraic field is the domain for many areas of mathematics, including real and complex analysis. We saw in Section 4.2 that the real numbers were a complete ordered field.
When one thinks of a field, one thinks of a structure with two operations resembling addition and multiplication, where one can add, subtract, multiply, and divide. The reader is well aware of three common fields from analysis, the rational numbers ℚ, the real numbers ℝ, and the complex numbers ℂ. There are “hypercomplex” number systems past the complex numbers, like four‐dimensional quaternions and the eight‐dimensional octonians, neither of those number systems are fields, but more general abstract systems. Quaternion multiplication does not commute, and octonian multiplication not only does not commute but also is not even associative.
6.5.4 Finite Fields
Although we think of the rational numbers ℚ, the real numbers ℝ, and the complex numbers ℂ as the major infinite fields, there are many important finite fields, which contain only a finite number of elements. Finite fields play an important role in many areas of mathematics, including algebraic geometry and number theory, as well as applied areas like coding theory and cryptography.
An interesting property of finite fields is that they exist only for certain orders. For example there are finite fields of order 2, 3, 4, and 5, but none of order 6. There are finite fields of order 7, 8, 9, but none of order 10. To be specific, there are finite fields of order pn, n = 1, 2, … where p is a prime number, but no others. These finite fields are called Galois fields and denoted by GF(pn).4
There are two main classifications of finite fields. There are the finite fields GF(p) of prime order and then the more involved fields of order pn when n > 1. The prime order fields GF(p), when n = 1, are the field of permutations ℤp = {0, 1, 2, … , p − 1} of integers with addition and multiplication carried out modulo p. However, we saw in Example 8 that ℤ6 = {0, 1, 2, 3, 4, 5} is not a field since 6 is not a prime number.

Figure 6.58 Arithmetic operations for the field GF(7) = ℤ7.
Problems
- True or False
- A ring can be finite or infinite.
- In a ring {R, +, ×}, the set R with × is a group.
- In a ring {R, +, ×}, the set R with + is a group.
- The ring ℤ11 is also a field.
- The ring ℤ8 is also a field.
- There are fields where a × b = 0, but neither a, b are zero.
- Multiplicative Identity
For each of the following rings, tell if the ring is commutative and if there exists a multiplicative identity. If a multiplicative identity exists, what is it?
- The ring of integers ℤ with usual addition and multiplication.
- The ring of even integers 2ℤ with usual addition and multiplication.
- The ring C(ℝ) of real‐valued continuous functions with usual addition and multiplication.
- The ring consisting of the set
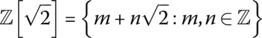
with usual addition and multiplication.
- The ring ℤ[x] of all polynomials in x whose coefficients are integer with ordinary addition and multiplication.
- The ring ℚ of rational numbers with ordinary addition and multiplication.
- The ring consisting of the set ℤ3 = {0, 1, 2} where addition and multiplication are defined modulo 3.
- Ring of Matrices
Show that the set of all 2 × 2 matrices
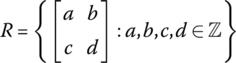
is a ring under matrix addition and matrix multiplication, but not a field.
- Rings that are not Fields
Why do the following rings fail to be fields?
- The ring of polynomials with real coefficients with the usual addition and multiplication.
- The ring of n × n matrices with the usual matrix addition and multiplication.
- The set ℤn = {0, 1, 2, … , n − 1}, where the operations of addition and multiplication are performed mod n, where n is a composite natural number.
- Modulo 3 Field
The addition and multiplication tables for ℤ3 are shown in Figure 6.59. What are the additive and multiplicative inverses for each member of the field?
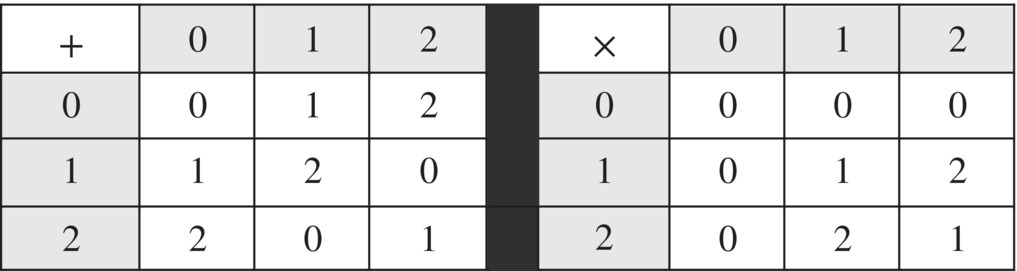
Figure 6.59 Modulo 3 field.
- Construct the addition and multiplication tables for ℤ5.
- Arithmetic in ℤ3
In the field GF(3) = ℤ3, compute the following.
- 1 + 2
- 1 − 2
- 2 × 2
- 1/2
- Modular Algebra
Find values of x that satisfies the following equations.
- 2x = 1(mod3), x ∈ ℤ3
- 3x = 2(mod5), x ∈ ℤ5
- 4x = 3(mod7), x ∈ ℤ7
- Multiplicative Inverse
The integers ℤ under usual addition and multiplication form a commutative ring with unity 1. Do any members of this ring have multiplicative inverses? If so, what are they?
- More Modular Algebra
Solve the equation 7x – 3 = 5 in ℤ24.
- Type of Ring
The set {0, a, b, c} with operations of addition and multiplication, defined by the tables in Figure 6.60, forms a ring. Is this group commutative and does it have a multiplicative identity?
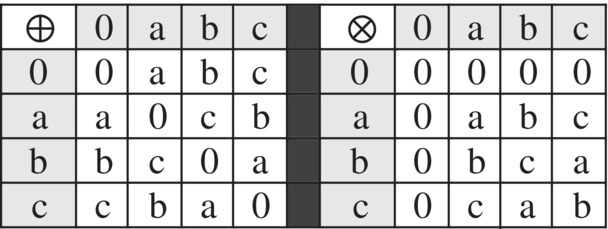
Figure 6.60 Special ring.
Zero Divisors
In some rings, things do not obey the arithmetic you learned in grade school. For example in the ring ℤ4 = {0, 1, 2, 3} modulo 4 arithmetic, we found 2 × 2 = 0. In this case, we say that 2 is a zero divisor for this ring. In general, an element a ∈ R in a ring is a zero divisor if there is a nonzero element b ∈ R in the ring such that ab = 0. Matrix rings also have zero divisors.
- Zero Divisors
Find a zero divisor in the ring of 3 × 3 matrices with integer entries using the usual operations of addition and multiplication?
- Internet Research
There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward importance of ring theory in mathematics, importance of field theory in mathematics, important rings and fields in mathematics, history of ring theory in mathematics, and history of field theory in mathematics.
