2.5 Context-Free Languages and Grammars

There is a limit on the expressivity of regular expressions and regular grammars. In other words, some languages cannot be defined by a regular expression or a regular grammar. As a result, there are also computational limits on the sentence-recognition capabilities of finite-state automata. Consider the language L of balanced parentheses, whose sentences are strings of nested parentheses with the same number of opening parentheses in the first half of the string as closing parentheses in the second half of the string: 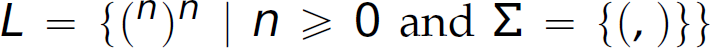. The strings 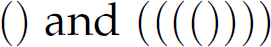are balanced and, therefore, sentences in this language; conversely, the strings 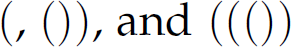are unbalanced and not in the language. In formal language theory, a language of strings of balanced parentheses is called a Dyck language. A Dyck language cannot be defined by a regular expression. Alternatively, consider the language L of binary palindromes—binary numbers that read the same forward as backward: 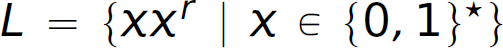, where means “a reversed copy of χ.” The strings 00, 11, 101, 010, 1111, and 001100 are in the language, but 01, 10, 1000, and 1101 are not. We cannot construct either a regular expression or a regular grammar to define these languages. In other words, neither a regular expression nor a regular grammar has the expressive capability to model these languages.

What capability is absent from regular expressions or regular grammars that renders them unusable for defining these languages? Consider how we might implement a computer program to recognize strings of balanced parentheses. We could use a stack data structure to match each opening parenthesis with a closing parenthesis. Whenever we encounter an open parenthesis, we push it onto the stack; whenever we see a closing parenthesis, we pop from the stack. If the stack is empty when all the characters in the string are consumed, then the parentheses in the string are balanced and the string is a sentence; otherwise, it is not. The utility of a stack (formally, a pushdown automata) for this purpose implies that we need some form of unbounded memory to the match parentheses in the candidate string (i.e., to keep track of the number of unclosed open parentheses unknown a priori). Recall that the F in FSA stands for finite.

While regular expressions can denote the lexemes (e.g., identifiers) of programming languages, they cannot model syntactic structures nested arbitrarily deep that involve balanced pairs of lexemes (e.g., matched curly braces or begin/end keyword pairs identifying blocks of code; or parentheses in mathematical expressions), which are ubiquitous in programming languages. In other words, a sequence of lexemes in a program must be arranged in a particular order, and that order cannot be captured by a regular expression or a regular grammar. Regular expressions are expressive enough to denote the lexemes of programming languages, but not the higher-order syntactic structures (e.g., expressions and statements) of programming languages. Therefore, we must turn our attention to formal grammars with greater expressive capabilities than regular grammars if we need to define more sophisticated formal languages, including, in particular, programming languages.

Level 2 of the Chomsky hierarchy defines a type of formal grammar, called a context-free grammar, which is most appropriate for defining (and, as we see later, implementing) programming languages. Like the production rules of a regular grammar, the productions of a context-free grammar must conform to a particular pattern, but that pattern is less restrictive than the pattern to which regular grammars must adhere. The productions of a context-free grammar may have only one non-terminal on the left-hand side. Formally, a grammar is a context-free grammar if and only if every production rule is in the following form:

X → γ

where 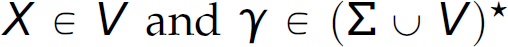, there is only one non-terminal on the left-hand side of any rule, and X can be replaced with γ anywhere. Notice that since this definition is less restrictive than that of a regular grammar, every regular grammar is also a context-free grammar, but the reverse is not true.

Context-free grammars define a class of formal languages called context-free languages. The concept of balanced pairs of syntactic entities—the essence of a Dyck language—is at the heart of context-free languages. This single syntactic feature (and its variations) distinguishes regular languages from context-free languages, and the capability of expressing balanced pairs is the essence of a context-free grammars.