CHAPTER V

THE COMPLEX QUADRIC

1. Outline

This chapter is devoted to the complex quadric which plays a central role in the rigidity problems. In 2 and 3, we describe the differential geometry of the quadric viewed as a complex hypersurface of the complex projective space . We show that is a Hermitian symmetric space and a homogeneous space of the group SO(n + 2). The involutions of the tangent spaces of which arise from the second fundamental form of the quadric, allow us to introduce various objects and vector bundles on In particular, we decompose the bundle of symmetric 2-forms on into irreducible SO(n+2)-invariant sub-bundles; one of these bundles L, which is of rank 2, was first introduced in [18]. In 4, we develop the local formalism of Kahler geometry on the complex quadric following [22]; we wish to point out that auspicious choices lead to remarkably simple formulas. The identification of the quadric with the Grassmannian of oriented 2-planes in given in 5 allows us to relate the geometries of these two manifolds and to define the objects introduced in 3 in an intrinsic manner. In the next section, we describe the tangent spaces of various families of totally geodesic submanifolds of and present results concerning the spaces of tensors of curvature type which vanish when restricted to some of these families. In 7, we determine explicitly the space of infinitesimal Einstein deformations of and, from the point of view of harmonic analysis on homogeneous spaces, we compute the multiplicities of a class of isotypic components of the SO(n+2)-module of complex symmetric 2-forms on and establish properties of these components. Finally, 8 is devoted to results concerning sections of the sub-bundle in 9, we prove that the complex quadric is isometric to the product of spheres S2 × S².

2. The complex quadric viewed as a symmetric space

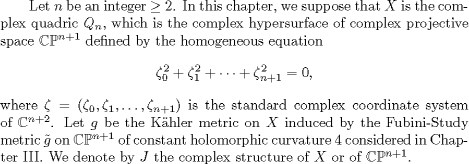
for If we identify Tb with by means of this isomorphism , since for the complex structure of Tb is the one determined by the multiplication by i on and the Kahler metric g at b is the one obtained from the standard Hermitian scalar product on given by (3.6). Moreover, by (5.1) we see that the action of the element

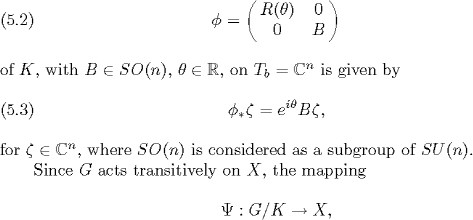
which sends the class , where , into the point is a diffeo-morphism compatible with the actions of G on G/K and X.

The element of K belongs to the center of K and is of order 4. The element of G determines an involution of G which sends G into . Then K is equal to the identity component of the set of fixed points of and (G,K) is a Riemannian symmetric pair. The Cartan decomposition of the Lie algebra of G corresponding to is

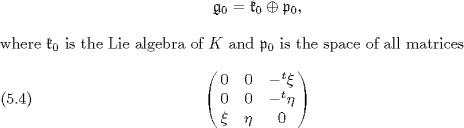
of , where are vectors of considered as column vectors. We identify with the tangent space of G/K at the coset of the identity element of G and also with the vector space in particular, the matrix (5.4) of p0 is identified with the vector )

If B is the Killing form of g0, the restriction to of the scalar product -B is invariant under the adjoint action of K and therefore induces a G-invariant Riemannian metric on the homogeneous space G/K. The restriction of Ad j to is a K-invariant complex structure on p0 and so gives rise to a G-invariant almost complex structure on G/K. According to Proposition 4.2 in Chapter VIII of [36], this almost complex structure is integrable and the manifold G/K, endowed with the corresponding complex structure and the metric, is a Hermitian symmetric space. The space G/K is of compact type and of rank 2; when n 3, it is irreducible.

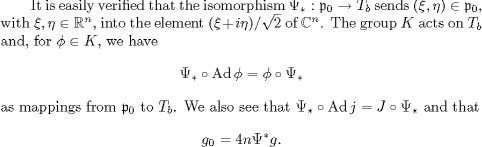
Thus is a holomorphic isometry from the Hermitian symmetric space G/K, endowed with the metric (1/4n) g0, to X; henceforth, we shall identify these two Kahler manifolds by means of this isometry. According to formula (1.65), it follows that X is an Einstein manifold and that its Ricci tensor Ric is given by

3. The complex quadric viewed as a complex hypersurface

We begin by recalling some results of Smyth [49] (see also [21]). The second fundamental form C of the complex hypersurface X of is a symmetric 2-form with values in the normal bundle of X in . We denote by S the bundle of unit vectors of this normal bundle.

from the last two equalities, we infer that the relation (5.21) also holds in this case. Thus we have shown that

The remainder of this section is devoted to results of [21] and [23]. We consider the sub-bundle L of introduced in [18], whose fiber at x X is equal to

C according to (5.9), if Sx, this fiber Lx is generated by the elements and and so the sub-bundle L of is of rank 2. We denote by the orthogonal complement of L in By (5.8), we see that L is stable under the endomorphism (1.68) of since the automorphism J of T is an isometry, the orthogonal complementof L in is also stable under this endomorphism. We denote by L, Land the eigenbundles corresponding to the eigenvalues +i and -i of the endomorphism of induced by the mapping (1.68). In fact, we have the equalities

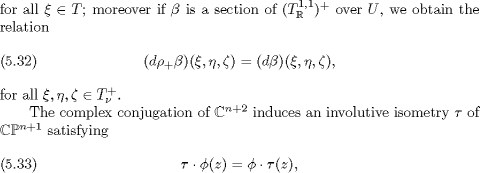
for all G and moreover preserves the submanifold X of The group of isometries of X generated by , which is of order 2, acts freely on X and we may therefore consider the Riemannian manifold with the metric gY induced by g, and the natural projection , which is a two-fold covering. By (5.33), we see that the action of the group G on X passes to the quotient Y ; in fact, the group G acts transitively on Y . If is the subgroup of O(n+2)

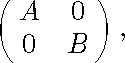
where it is easily verified that the isotropy group of the point is equal to the subgroup of G. We know that is a symmetric space of compact type of rank 2, which we may identify with Y by means of the isometry

sending into the point for G. Then by (5.33), we see that the projection is identified with the natural submersion of symmetric spaces.

Clearly, we have

4. Local Kähler geometry of the complex quadric

We now introduce the formalism of Kahler geometry on the complex quadric X = with n 2, developed in [22, 4].

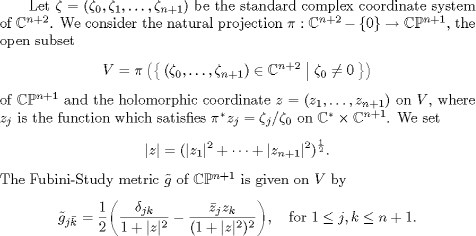
and for 1 j n. Thus since the group G = SO(n + 2) acts transitively on X, if x is a given point of X, from the preceding remark and (5.14) we infer that there exist a section of S over a neighborhood of x and an orthonormal frame for the vector bundle over satisfying for 1 j n.

If a is the point of S2n+3, then we note that (a) = a; moreover,

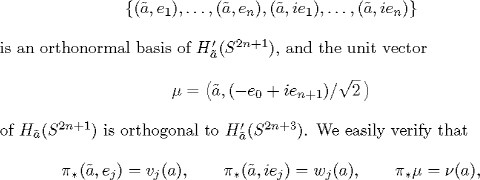
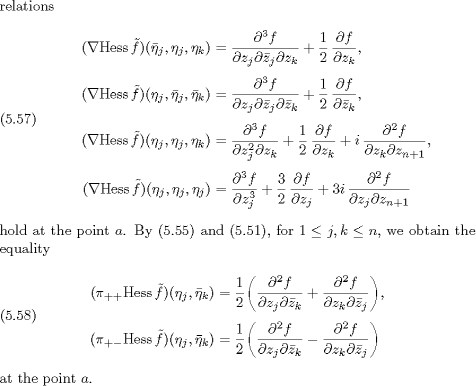
5. The complex quadric and the real Grassmannians

We also consider as the standard basis of . We consider the real Grassmannian of oriented 2-planes in which is a homogeneous space of G = SO(n + 2), endowed with the Riemannian metric defined in 1, Chapter IV and denoted there by g; we also consider the homogeneous vector bundles V and W over G

We define an almost complex structure J on as follows. If x and is a positively oriented orthonormal basis of the oriented 2-plane Vx, the endomorphism J of Vx, determined by

is independent of the choice of basis of Vx and we have J2 = -id. Clearly, the almost complex structure J of , which is equal to id on the tangent space ( of is invariant under the group G. Since ,n4.2 in Chapter VIII of [36], this almost complex structure J is integrable and the manifold endowed with the corresponding complex structure and the metric is a Hermitian symmetric space.

The sub-bundles and (S2T)+- of can be defined directly in terms of the intrinsic structure of the real Grassmannian without having recourse to the imbedding of X as a complex hypersurface of by

From the above inclusions, the relations (5.64) and (5.65), and the decompositions (4.6) and (5.26), we obtain the equalities

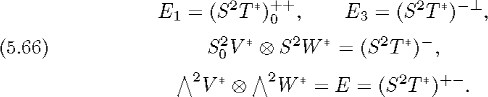
We now suppose that n is even. In 1, Chapter IV, we saw that the oriented 2-plane x X determines an orientation of the space Wx. Let x be a point of X and let be an element of Sx. We say that an orthonormal basis of is positively (resp. negatively) oriented if there is a positively oriented orthonormal basis {v1, v2} of Vx and a positively (resp. negatively) oriented orthonormal basis {w1, . . . ,wn} of Wx such that

for Since n is even, it is easily seen that the notions of positively and negatively oriented orthonormal bases of are well-defined. Also an arbitrary orthonormal basis of is either positively or negatively oriented.

We now consider the case when n = 4. The orientations of the spaces a, with a X, and the scalar product g2 give rise to a Hodge operator

By formulas (3.6) of [21] and (5.68), we easily verify that this auto-morphism of the vector bundle is equal to the involution of the vector bundle ( defined in [21, 3] in terms of an appropriate orientation of the real structures of X. Thus the eigenbundles F+ and F- of this involution of corresponding to the eigenvalues +1 and -1, which are considered in [21, 3], are equal to respectively. The decomposition + and

LEMMA 5.2. Let X be the quadric For all we have

6. Totally geodesic surfaces and the infinitesimal orbit of the curvature

We begin by giving an explicit representation of the infinitesimal orbit of the curvature of the complex quadric X = with n 3.

for all 2 From formulas (1.72) and (5.10), it follows that

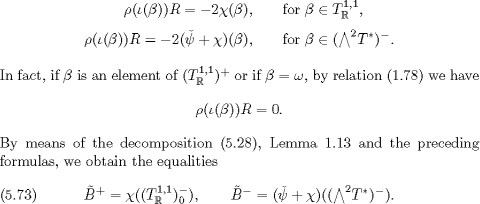
We now introduce various families of closed connected totally geodesic submanifolds of X. Let x be a point of X and be an element of Sx. If is an orthonormal set of vectors of , according to formula (5.10) we see that the set ExpxF is a closed connected totally geodesic surface of X, whenever F is the subspace of Tx generated by one of following families of vectors:

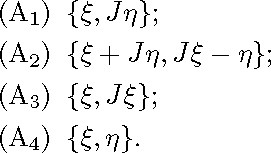
According to [10], if F is generated by the family (A2) (resp. the family (A3)) of vectors, where {, } is an orthonormal set of vectors of the surface ExpxF is isometric to the complex projective line with its metric of constant holomorphic curvature 4 (resp. curvature 2). Moreover, if F is generated by the family (A1), where is an orthonormal set of vectors of the surface ExpxF is isometric to a flat torus.

For 1 j 4, we denote by the set of all closed totally geodesic surfaces of X which can be written in the form ExpxF, where F is a subspace of Tx generated by a family of vectors of type (Aj ).

According to 5, there exists a unit vector v of Vx such that an arbitrary submanifold Z belonging to the family can be written in the form Expx where is a two-dimensional subspace of Wx. We consider the Riemannian metric on the Grassmannian defined in Chapter IV; by Lemma 4.6 and the relation (5.59), we see that the submani-fold Z is isometric to the Grassmannian endowed with the Riemannian metric Therefore such a submanifold Z is isometric to a sphere of constant curvature 2 (see also [10]); moreover, by Lemma 4.6 we also see that the image of Z under the mapping is a closed totally geodesic surface of Y isometric to the real projective plane endowed with its metric of constant curvature 2.

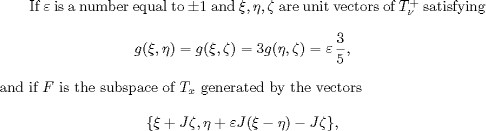
according to (5.10) we also see that the set ExpxF is a closed connected totally geodesic surface of X. Moreover, according to [10] this surface is isometric to a sphere of constant curvature 2/5. We denote by F5,the set of all such closed totally geodesic surfaces of X.

If is an orthonormal set of vectors of and if F is the subspace of Tx generated by the vectors

according to (5.10) we see that the set ExpxF is a closed connected totally geodesic surface of X. Moreover, according to [10] this surface is isometric to the real projective plane of constant curvature 1. Clearly such submanifolds of X only occur when n 4. We denote by the set of all such closed totally geodesic surfaces of X.

If is an orthonormal set of vectors of and if F is the subspace of Tx generated by the vectors

according to (5.10) we see that the set ExpxF is a closed connected totally geodesic submanifold of X. Moreover, this submanifold is isometric to the complex projective plane of constant holomorphic curvature 4. Clearly such submanifolds of X only occur when n 4. We denote by the set of all such closed totally geodesic submanifolds of X.

When n 4, clearly a surface belonging to the family F2,or to the family is contained in a closed totally geodesic submanifold of X belonging to the family F7,. In fact, the surfaces of the family F2,(resp. the family correspond to complex lines (resp. to linearly imbedded real projective planes) of the submanifolds of X belonging to the family viewed as complex projective planes.

Let Z be a surface belonging to the family with 1 j 6; we may write Z = ExpxF, where F is an appropriate subspace of Tx. Clearly, this space F is contained in a subspace of Tx which can be written in the form where F1 is a subspace of of dimension ; we may suppose that this integer k is given by

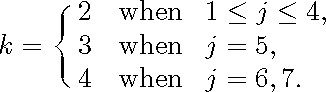
According to observations made in 5, the surface Z = ExpxF is contained in a closed totally geodesic submanifold of X isometric to the quadric where W1 is a subspace of Wx of dimension k.

Let F^x be the family of all closed connected totally geodesic submani-folds of X passing through x which can be written as where

xW1 is a subspace of Wx of dimension 3. We know that a submanifold of X belonging to F is isometric to the quadric of dimension 3.

of closed connected totally geodesic submanifolds of X isometric to Q3. We have seen that a surface belonging to the family with 1 j 5, is contained in a closed totally geodesic submanifold of X belonging to the family F.

Since the group G acts transitively on the set of all maximal flat totally geodesic tori of X and also on a torus belonging to and since a surface of is a flat 2-torus, we see that, if Z is an element of and if x is a point of Z, there exists an element Sx and an orthonormal set of vectors

It follows that the family F1 is equal to .

In [10], Dieng classified all closed connected totally geodesic surfaces of X and proved the following:

PROPOSITION 5.3. If n 3, then the family of all closed connected totally geodesic surfaces of X is equal to

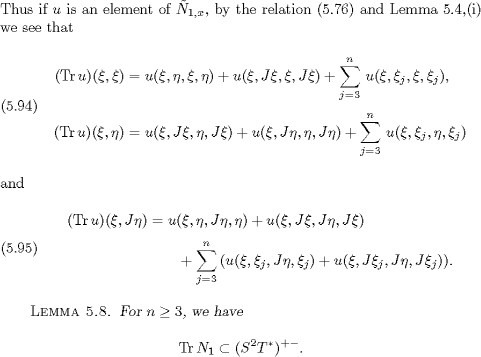
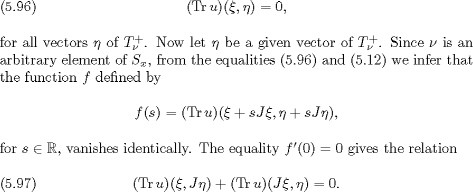
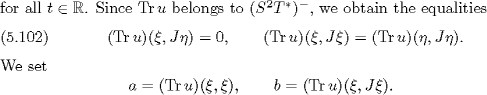
This inclusion and (5.84) give us the first relation of (5.98). Now suppose that u belongs to When n 5, by Lemma 5.7 we know that the relation (5.80) holds; then according to the first formula of (5.94) and Lemma 5.6,(iv), we see that the expression (Tr u) vanishes. When n = 4, according to the first formula of (5.94) and the equalities (5.87) of Lemma 5.5, we have

vanishes. Hence according to (5.95), the expression (Tr u) vanishes. Since Tr u belongs to we know that Thus we have proved assertion (ii).

The following two propositions are direct consequences of Proposition 5.9 and the second equality of (5.74), with j = 2. In fact, Proposition 5.11 is given by Proposition 5.1 of [21].

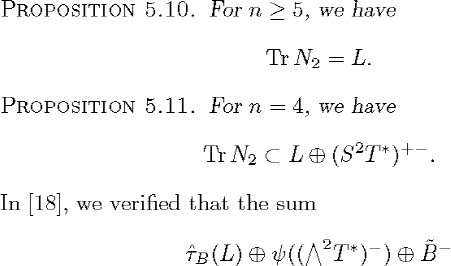
BB is direct; we also know that it is a sub-bundle of Using the relations 2 (1.79) and (5.73), in [18] we were able to determine the ranks of the vector bundles ⁺ an When n 5, by means of Lemmas 5.4–5.7 and other analogous results, in [21] we found explicit bounds for the ranks of the vector bundles and From these results, the relation (1.79), the second equality of (5.74) and the inclusion (5.75), with j = 2, we obtain the following proposition (see [18, 5]):

7. Multiplicities

In this section, we shall suppose that n 3. Let g and k denote the complexifications of the Lie algebras and k0 of G = SO(n + 2) and its subgroup K, respectively. Letand be the duals of the groups G and K, respectively.

We first suppose that n = 2m, with m 2. We set We choose Weyl chambers of and (k, t) for which the system of simple roots of g and k are equal to , and respectively. The highest weight of an irreducible G-module (resp. K-module) is a linear form

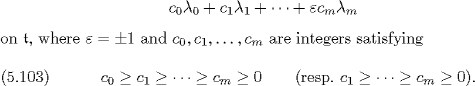
The equivalence class of such a G-module (resp. K-module) is determined by this weight. In this case, we identify (resp. with the set of all such linear forms on

which belong to and respectively. The complexification of admits the decomposition

where and are the eigenspaces of the endomorphism Ad j of p corresponding to the eigenvalues +i and -i, respectively. Since j belongs to the center of K, this decomposition of p is invariant under the action of K on p. We thus obtain the K-invariant decomposition

We consider the subgroup

of G, which we introduced in 3 and which contains the subgroup K. The decomposition (5.104) gives us the invariant decomposition

According to the equalities (5.108) and (5.109) and Proposition 2.40, since the symmetric space X is irreducible and is not equal to a simple Lie group, we see that E(X) vanishes when n 4, and that E(X) is isomorphic to the G-module when n = 4. By Lemma 5.15 and the Frobenius reciprocity theorem, we see that

if n 4, then Lemma 5.15 tells us that is an irreducible G-module.

When the vanishing of the space E(X) is also given by Theorem 1.22 (see Koiso [41] and [42]).

From the branching law for G = SO(n + 2) and K described in Theorems 1.1 and 1.2 of [54], using the computation of the highest weights of the irreducible K-modules given above we obtain the following two propo-sitions:

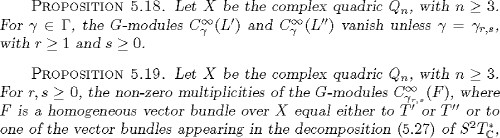
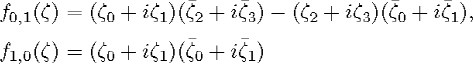
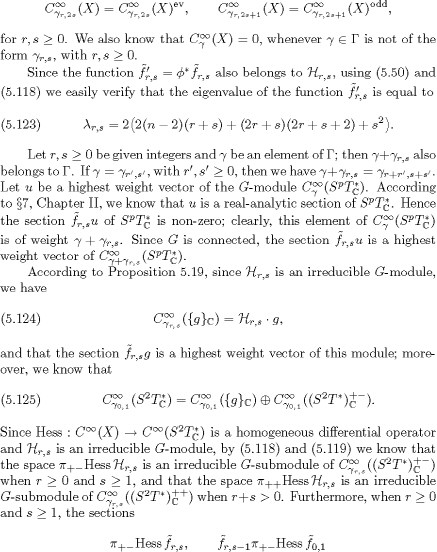
where b1, b2 are complex numbers which do not both vanish, and that there is a non-zero constant such that the relation (5.128) holds. From these remarks, we obtain the following equalities among irreducible G-modules

We no longer assume that n = 4 and return to the situation where n is an arbitrary integer 3. Since Hess is a

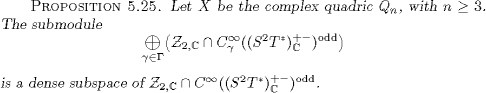
8. Vanishing results for symmetric forms

This section is mainly devoted to results concerning the sections of the vector bundle L and to the proofs of the following two results:

PROPOSITION 5.26. Let X be the complex quadric with n 3. A section h of L over X, which satisfies the relation div h = 0, vanishes identically.

Theorem 5.27. Let X be the complex quadric with n 3. An even section of L over X, which belongs to the space vanishes identically. Moreover, we have the equality

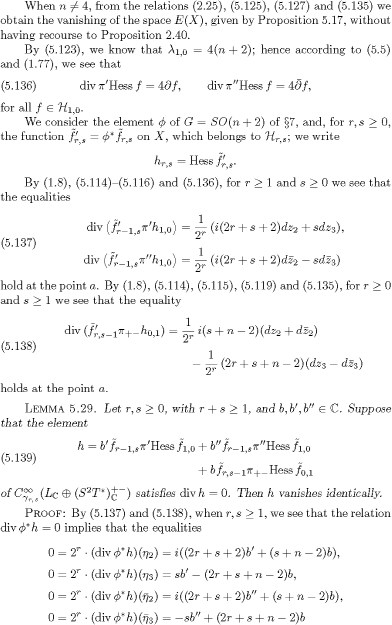
hold at a. Since the determinant of the matrix

is positive, when r, s 1 the coefficients band b vanish, and so in this case h vanishes. Since

when either r = 0 or s = 0, by (5.138) and (5.139) we see that the relation div = 0 implies that h vanishes.

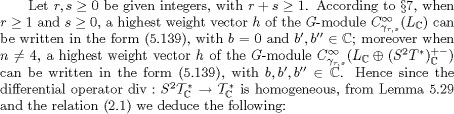
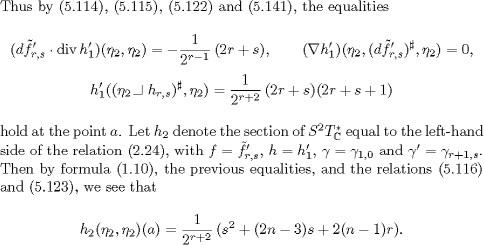
satisfies From Proposition 5.31, we therefore obtain the relation According to our hypothesis, hbelongs to the space and so the other assertion of the proposition is a consequence of Proposition 5.32.

Let 0 be given integers. According to Proposition 5.33 and the description of the highest weight vectors of the G-module given above, we see that the space

Since D0 is a homogeneous differential operator, by Proposition 5.18 and the relations (2.1) and (5.133), we see that Theorem 5.27 is a consequence of these results.

9. The complex quadric of dimension two

We endow the manifold with the Kahler metric which is the product of the metrics on each factor. It is well-known that the Segre imbedding

We consider the involutive isometry of defined in 4, Chapter III; according to the commutativity of diagram (3.26), it sends the point where is a non-zero vector of into the point where is a non-zero vector of orthogonal to u. We easily verify that the diagram

is commutative.

Now we consider the diffeomorphism defined in 5 and the involutive isometry of defined in 1, Chapter IV, which sends an oriented 2-plane of into its orthogonal complement endowed with the appropriate orientation. If is the involutive isometry equal to the composition the diagram

The commutativity of the diagram (5.143) is now a consequence of the relations