CHAPTER VI

THE RIGIDITY OF THE COMPLEX QUADRIC

1. Outline

2. Totally geodesic flat tori of the complex quadric

Throughout this chapter, we suppose that X is the complex quadric with n3, endowed with the Kähler metric g introduced in 2, Chapter V. We shall consider the objects and use the notations established in Chapter V.

If Z is a flat totally geodesic 2-torus of X, we denote by ^Z the LeviCivita connection of the Riemannian manifold Z endowed with the metric induced by g; if is a vector field on Z, we consider the complex vector fields on X defined along Z by

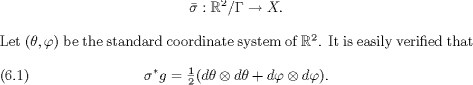
Therefore, if the quotient is endowed with the flat metric induced by the metric on R2, the mapping is a totally geodesic isometric imbedding. Throughout this chapter, we shall often identify a function f on satisfying

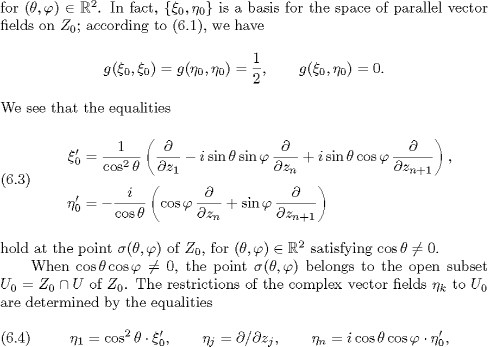
with 2 which hold at the point (, ) whenever

2 satisfies cos cos = 0. We consider the section of the bundle S over U given by (5.40) and the involutive endomorphism Kof defined by K(x) = K(x), for x U; from the relation (5.51), we obtain the equalities

on the open subset U0 of Z0. It follows that the restriction of this involution K to satisfies

As in Chapter II, we denote by the space of all maximal flat totally geodesic tori of X. Since the point a belongs to Z0, according to the description of given in 6, Chapter V, we see that

LEMMA 6.1. Let Z be a totally geodesic flat 2-torus of X and let x0 Z. Then there exist an open neighborhood of x0 in Z, an involution of T|Uwhich preserves the tangent bundle of Z and a section of S over such that for all Moreover, the restriction ofthis involution to TZ is an endomorphism of which is parallel with respect to the connection

PROOF: Since the group G acts transitively both on and on the torus without loss of generality by (5.14) we may assume that Z is the torus Z0 described above and that x0 is the point a of the subset U0 of Z0. Then if is the section of S over U given by (5.40), according to (6.6) we know that the involution Kof preserves the tangent bundle of Z0. Let , be tangent vectors to Z0 at x U0; if is the restriction of the involution Kto TZ0 , we know that

(^Z)= (K).

According to (5.22), the right-hand side of this equality belongs to since Z0 is a totally real submanifold of X, it vanishes. Thus we have = 0.

LEMMA 6.2. Let Z be a totally geodesic flat 2-torus of X. Then there exists a unique (up to a sign) involution of which preserves the tangent bundle of Z and which at every point x of Z is equal to a real structure Kì of X, where . Moreover, the restriction of this involution to TZ is an endomorphism of TZ which is parallel with respect to the connection

PROOF: Let x be a point of Z. According to 6, Chapter V, we may write

where ì is an appropriately chosen element of Sx and is an orthonor-mal set of elements of Clearly, preserves the tangent space to Z at x. According to (5.9), a real structure of the quadric X associated with another unit normal of Sx can be written in the form

where R. We see that preserves the tangent space to Z at x if and only if sin = 0, that is, if = ±Kì. From this observation and the orientability of Z, by Lemma 6.1 we obtain the desired endomorphism of T|Z; clearly, it is unique up to a sign and is parallel with respect to the connection

The involution , which Lemma 6.2 associates with a totally geodesic flat 2-torus Z contained in X, is called a real structure of the torus Z; it is uniquely determined up to a sign.

According to Lemma 6.2 and its proof, there exists a unique real structure 0 of the torus Z0 such that

and we know that the vector fields and on Z0 are parallel. Hence by (6.5), we see that

and that the restriction of 0 to U0 is equal to the involutive endomorphism Kof

| Let Z be a totally geodesic flat 2-torus contained in X; we choose a real structure of Z. Since the restriction of to TZ is parallel, the tangent bundle TZ admits an orthogonal decomposition

Z and are the eigenbundles of the restriction invariant under where of to TZ, corresponding to the eigenvalues +1 and -1. Clearly, this decomposition of TZ is independent of the choice of . It is easily seen that there exist unitary parallel sections of and of these two vector fields are unique up to a sign and is a basis for the space of parallel vector fields on Z.