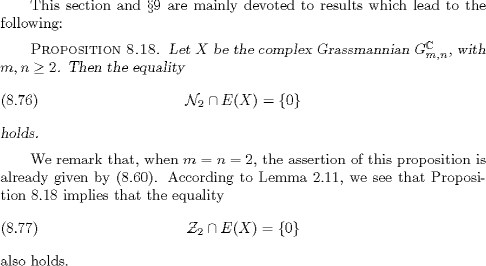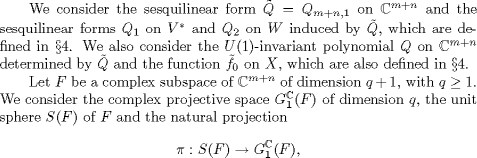CHAPTER VIII

THE COMPLEX GRASSMANNIANS

1. Outline

This chapter is devoted to the geometry of the complex Grassmanni-ans. In 2, we study the complex Grassmannian GC of complex m-planes m,n in Cm+n, with m, n 2, and show that it is a Hermitian symmetric space and a homogeneous space of the group SU(m + n); we also consider the Grassmannian GCn,n, which is the adjoint space of GC n,n. We introduce certain vector bundles over GC m,n and use them to decompose the bundle of symmetric 2-forms on GC m,n into irreducible SU(m + n)-invariant sub-bundles. We then determine the highest weights of the fibers of these vector bundles in 3. We define certain complex-valued functions on GC m,n by means of the corresponding Stiefel manifold; then these functions and specific symmetric 2-forms on GC m,n, arising from the complexification g of the Lie algebra of SU(m+n), allow us to describe explicitly and study the SU(m+n)-modules of functions and complex symmetric 2-forms on GC m,n isomorphic to g. In particular, we examine the case when m = n and determine explicitly the space of infinitesimal Einstein deformations of GC n,n. In 5, we define the natural isometry between the Grassmannian GC2 ,2 and the complex quadric Q4 and use it to relate their geometries; from the results of Chapter VI, it follows that this complex Grassmannian is infinitesimally rigid and that its quotient G

C2 ,2 is rigid in the sense of Guillemin. In the next section, we show that the Guillemin condition for forms on GC m,n, with m = n, is hereditary with respect to certain totally geodesic subman-ifolds. The remainder of this chapter is mainly devoted to the proof of the following result, which plays an essential role in our study of the rigidity of the complex Grassmannians presented in Chapter IX: an infinitesimal Einstein deformation of GC m,n satisfying the Guillemin condition vanishes. In order to prove this result in the case when m = n, we compute the integrals of some of the symmetric 2-forms considered in 4 over explicit closed geodesics. By means of these computations, in 8 we also establish relations among the symmetric 2-forms of 4. Finally, in 9 we study forms on the Grassmannian GC n,n and we introduce an averaging process which assigns to a p-form u on GCn +1,n+1 a class of p-forms on GC n,n that are obtained by integrating u over closed geodesics. We then consider a certain 1 on GC explicit complex symmetric 2-form h(n

) n,n and show that one of the 1 on GCn+1,n+1 is equal to the form h(n) averages of the 2-form h(n+1) 1 . From this last result, we deduce by induction on n that an Einstein deformation of the space GC n,n which satisfies the Guillemin condition vanishes.

2. The complex Grassmannians

Let X be a manifold and let E be a real vector bundle over X endowed with a complex structure J. The complexification EC of E admits the decomposition

the bundles S^p,qT*and ^p,qT*coincide with the bundles associated above with the vector bundle E = T.

Let m, n 0 be given integers and let F be a complex vector space of dimension m+n endowed with a positive definite Hermitian scalar product. We now suppose that X is the complex Grassmannian GC m(F) of all complex m-planes in F; then X is a complex manifold whose complex structure we denote by J. If either m = 0 or n = 0, the manifold GC m(F) is a point. When m = 1, the manifold GC1 (F) is the complex projective space of all complex lines of F.

Since the vector bundles V and W are complex sub-bundles of the trivial complex vector bundle over X whose fiber is F, a sesquilinear form on F induces by restriction sesquilinear forms on the vector bundles V and W. In particular, the Hermitian scalar product on F induces by restriction positive definite Hermitian scalar products g1 and g2 on the vector bundles V and W, respectively. We consider the mappings

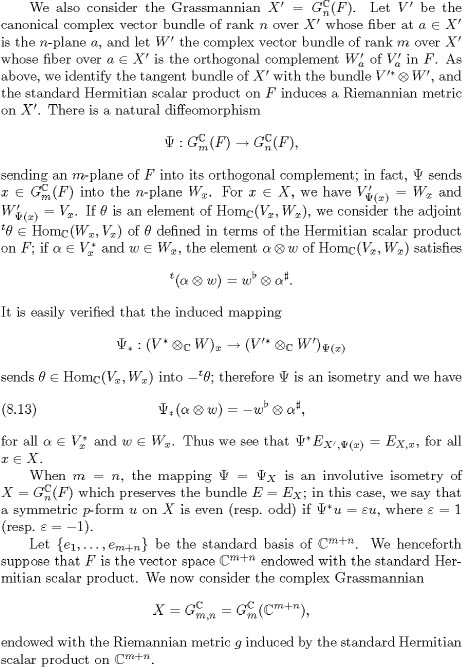
The action of the group G = SU(m + n) on Cm+n gives rise to an action of G on X. In fact, the group G acts transitively on the Rieman-nian manifold (X, g) by holomorphic isometries. The isotropy group of the point x0 of X equal to the m-plane Vx0 of Cm+n spanned by the vectors

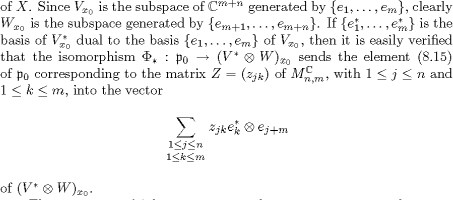
The restriction of Ad j to p0 is a complex structure on p0, and so gives rise to a G-invariant complex structure on G/K. If B is the Killing form of g0, the restriction to p0 of the scalar product -B is invariant under the adjoint action of K and therefore induces a G-invariant metric g0 on the homogeneous space G/K. Endowed with this complex structure and the metric g0, the manifold G/K is an irreducible Hermitian symmetric space of compact type of rank min(m, n) (see Proposition 4.2 in Chapter VIII of [36]). When m = n, we easily see that the group KS is equal to K; then according to 9 in Chapter VII of [36], it follows that G/K is equal to its adjoint space.

The vector bundles V and W are homogeneous G-sub-bundles of the trivial complex vector bundle over X whose fiber is Cm+n. Therefore the tensor product V C W is a homogeneous G-bundle and it is easily seen that (8.1) is an isomorphism of homogeneous G-bundles over X. All the vector bundles appearing in the decomposition (8.11) and the bundle E are homogeneous sub-bundles of S2TC; hence the fibers at x0 of these vector bundles are K-submodules of S2TC,x0 . Moreover under the action of the group K on Cm+n, the subspaces Vx0 and Wx0 of Cm+n are preserved; in fact, the fiber Vx0 is a U(m)-module, while the fiber Wx0 is a U(n)-module. The fibers at x0 X of the vector bundles

and the morphisms of vector bundles (8.3) and (8.4) are G-equivariant, and hence the restrictions of these morphisms of vector bundles to the fibers at x0 are morphisms of K-modules. When m, n 2, we know that these morphisms of K-modules are non-zero. From these remarks, we infer that the morphism (8.20) is an isomorphism of vector bundles and that the mor-phisms of vector bundles (8.3) and (8.4) are injective. Since the rank of the vector bundles (S2V )⁺0and (S2W)⁺0are equal to m2 - 1 and n2 - 1, respectively, from the decomposition (8.7) we now see that the vector bundle E3 and its sub-bundle (S2V )+0 (S2W)+0have the same rank; we thus obtain the equality (8.10). On the other hand, by a dimension-counting argument, from the decomposition (8.2) we now obtain the equalities (8.5) and see that the morphisms (8.3) and (8.4) are isomorphisms. In fact, we have

From Proposition 2.18, we obtain the following:

PROPOSITION 8.2. The symmetric space GCn,n is rigid in the sense of Guillemin if and only if every even symmetric 2-form on GC n,n satisfying the Guillemin condition is a Lie derivative of the metric.

The notion of even (resp. odd) symmetric p-form on CP1 defined in 4, Chapter III, coincides with the one introduced here on GC1 ,1. Hence from Lemma 8.1 and Propositions 2.20 and 3.29, we obtain the following result:

PROPOSITION 8.3. Let X be the symmetric space G

C1 ,1.

(i) The X-ray transform for functions on X is injective.

(ii) A differential form of degree 1 on X satisfies the zero-energy condition if and only if it is exact.

Since the space G

C1 ,1 has rank one, the first assertion of this proposition is also given by Theorem 2.24.

3. Highest weights of irreducible modules associated with the complex Grassmannians

Let m, n 2 be given integers. We pursue our study of the complex Grassmannian X = GC m,n. We consider the Lie algebras g0 and k0 of the compact Lie group G = SU(m + n) and its subgroup K. The complexi-fication g of g0 is equal to sl(m + n,C), and the complexification k of the Lie algebra k0 admits the decomposition

is the system of roots of g with respect to t; if we set

are G-equivariant isomorphisms of vector bundles. Therefore the fibers at x0 of the homogeneous sub-bundles of S2TC which appear in the right-hand side of (8.11) are irreducible K-modules, and the morphism

4. Functions and forms on the complex Grassmannians

Let m, n 2 be given integers. In this section, we describe explicit functions and symmetric 2-forms on the complex Grassmannian X = GC m,n, which we view as a homogeneous space of the group G = SU(m + n).

Let Sm,n be the space of all complex (m + n) × m matrices A satisfying tAA = Im. We view Sm,n as the Stiefel manifold of all orthonormal m-frames in Cm+n; the matrix A of Sm,n determines the m-frame consisting of the m column vectors of A. The unitary group U(m) acts on Sm,n by right multiplication and we consider the quotient space Sm,n/U(m). The mapping

sending the element A of Sm,n into the m-plane spanned by the m column vectors of A, induces by passage to the quotient a diffeomorphism

are non-zero.

Since is

5. The complex Grassmannians of rank two

According to (5.59), the quotient of the complex quadric Q4 by the action of the group of isometries of Q4 generated by is isometric to the real Grassmannian GR2 ,4 endowed with the Riemannian metric ¹2 g, where g is the metric on GR2 ,4 considered in 1, Chapter IV. Hence the commu-tativity of diagram (8.58) implies that the space G

C2 ,2 is isometric to the Grassmannian GR2 ,4 endowed with this metric ¹2 g; moreover, a symmetric p-form u on the quadric Z is even (resp. odd) with respect to the involution if and only if the symmetric p-form u on GC2 ,2 is even (resp. odd). From Proposition 4.14 and Theorems 6.47 and 6.71, with n = 4, we deduce the following three results, the first of which is also given by Theorem 2.24:

The commutativity of the diagram (8.58), the isomorphisms (8.61) and Theorem 6.52 give us the following:

Theorem 8.11. Let X be the complex Grassmannian An even section of EX over X, which satisfies the Guillemin condition, vanishes identically.

6. The Guillemin condition on the complex Grassmannians

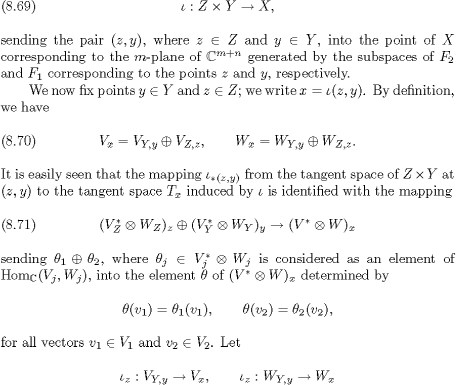
be the inclusion mappings corresponding to the decompositions (8.70). The first decomposition of (8.70) also determines an injective mapping

7. Integrals of forms on the complex Grassmannians