CHAPTER IX
THE RIGIDITY OF THE COMPLEX GRASSMANNIANS
1. The rigidity of the complex Grassmannians
By Lemmas 8.13 and 8.15, we know that a submanifold of X belonging to the family 
is isometric to the real Grassmannian 
and that a submanifold of X belonging to the family 
is isometric to the complex projective space 
of dimension n endowed with its Fubini-Study metric of constant holomorphic curvature 4.
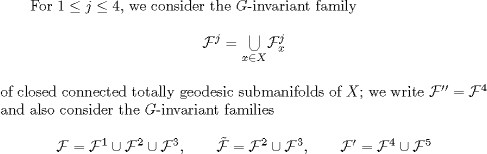
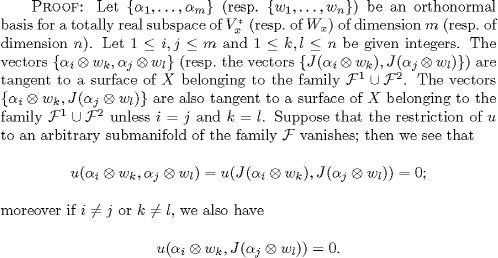
On the other hand, the vectors 
are tangent to a sub-manifold belonging to the family F3, and so we see that
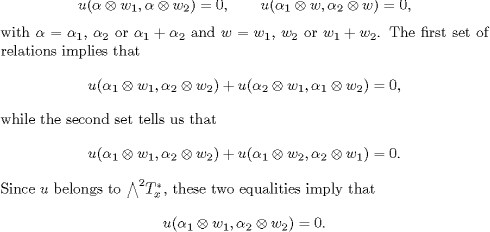
PROPOSITION 9.4. Let h be a section of E over the complex Grass-mannian X =
with m ≥ 2 and n≥ 3. If the restriction of h to an arbitrary submanifold Z of X belonging to the family 
is a Lie derivative of the metric of Z, then h vanishes.
2. On the rigidity of the complex Grassmannians 
and, when n 
3, that
Fh In the course of the previous discussion, we have proved the following proposition:
PROPOSITION 9.12. Let h be a symmetric 2-form and
be a 1-form on the complex Grassmannian 
with n
2.
holds.
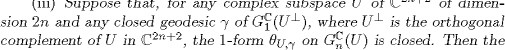
restriction of the 2-form dto an arbitrary submanifold of X belonging to the family 
vanishes.
3. The rigidity of the quaternionic Grassmannians
