INTRODUCTION

This monograph is motivated by a fundamental rigidity problem in Riemannian geometry: determine whether the metric of a given Rieman-nian symmetric space of compact type can be characterized by means of the spectrum of its Laplacian. An infinitesimal isospectral deformation of the metric of such a symmetric space belongs to the kernel of a certain Radon transform defined in terms of integration over the flat totally geodesic tori of dimension equal to the rank of the space. Here we study an infinitesimal version of this spectral rigidity problem: determine all the symmetric spaces of compact type for which this Radon transform is injective in an appropriate sense. We shall both give examples of spaces which are not infinitesimally rigid in this sense and prove that this Radon transform is injective in the case of most Grassmannians.

At present, it is only in the case of spaces of rank one that infinitesimal rigidity in this sense gives rise to a characterization of the metric by means of its spectrum. In the case of spaces of higher rank, there are no analogues of this phenomenon and the relationship between the two rigidity problems is not yet elucidated. However, the existence of infinitesimal deformations belonging to the kernel of the Radon transform might lead to non-trivial isospectral deformations of the metric.

Here we also study another closely related rigidity question which arises from the Blaschke problem: determine all the symmetric spaces for which the X-ray transform for symmetric 2-forms, which consists in integrating over all closed geodesics, is injective in an appropriate sense. In the case of spaces of rank one, this problem coincides with the previous Radon transform question. The methods used here for the study of these two problems are similar in nature.

Let (X, g) be a Riemannian symmetric space of compact type. Consider a family of Riemannian metrics {gt} on X, for , with g₀ = g. The family {gt} is said to be an isospectral deformation of g if the spectrum of the Laplacian of the metric gt is independent of t. We say that the space (X, g) is infinitesimally spectrally rigid (i.e., spectrally rigid to first-order) if, for every such isospectral deformation {gt} of g, there is a one-parameter family of diffeomorphisms of X such that to first-order in t at t = 0, or equivalently if the symmetric 2-form, which is equal to the infinitesimal deformation ^d of {gt}, is a Lie derivative of the metric g.

In [35], Guillemin introduced a criterion for infinitesimal spectral rigidity which may be expressed as follows. We say that a symmetric p-form u on X satisfies the Guillemin condition if, for every maximal flat totally geodesic torus Z contained in X and for all parallel vector fields on Z,

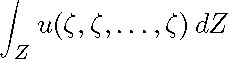
vanishes, where dZ is the Riemannian measure of Z. A symmetric 2form, which is a Lie derivative of the metric, always satisfies the Guillemin condition. Guillemin proved that a symmetric 2-form, which is equal to the infinitesimal deformation of an isospectral deformation of g, satisfies the Guillemin condition. We say that the space (X, g) is rigid in the sense of Guillemin if the following property holds: the only symmetric 2-forms on X satisfying the Guillemin condition are the Lie derivatives of the metric g. Thus if the symmetric space X is rigid in the sense of Guillemin, it is infinitesimally spectrally rigid.

We are interested in determining which symmetric spaces of compact type are infinitesimally spectrally rigid; in particular, we wish to find those spaces which are rigid in the sense of Guillemin. We show that an arbitrary non-trivial product of irreducible symmetric spaces of compact type, which are not equal to Lie groups, is not rigid in the sense of Guillemin. Consequently, we shall restrict our attention to irreducible spaces. We shall also see below that, in order for an irreducible space to be rigid in the sense of Guillemin, it must be equal to its adjoint space.

Although much work has been done on the problem of isospectrality, there are still very few results for positively curved spaces. All the previously known spectral rigidity results for symmetric spaces with positive curvature concern spaces of rank one. In fact, we will see below that the real projective space , with n 2, is spectrally rigid; on the other hand, for 2 n 6, the spectral rigidity of the sphere Sn was established by Berger and Tanno (see [4] and [51]). The Guillemin rigidity of the spaces of rank one (i.e., the projective spaces) which are not spheres was first proved by Michel [45] for the real projective spaces , with n 2, and by Michel [45] and Tsukamoto [53] for the other projective spaces. As we shall explain below, spectral rigidity results for these other projective spaces can be derived from their Guillemin rigidity by means of Kiyohara’s work [38].

In contrast to the case of negatively curved spaces, at present the problem of isospectrality for positively curved spaces does not admit any truly effective general approach. While the study of the symmetric spaces considered here requires a case by case analysis, we have nevertheless been able to develop criteria for rigidity which can be applied to numerous situations. Several fundamental aspects of differential geometry – the theory of overdetermined partial differential equations, deformation theory of Einstein manifolds, harmonic analysis on symmetric spaces of compact type, the geometry of the Grassmannians and their totally geodesic submanifolds – enter into the elaboration of these criteria and their application to the various spaces. Many of the results, which we present in the process, are of considerable interest in their own right outside the context of deformation theory and spectral rigidity.

In this monograph, we introduce new methods for studying the Guil-lemin rigidity of irreducible symmetric spaces of compact type. The theory of linear overdetermined partial differential equations of [28] provides us with a fundamental ingredient of these methods, namely a certain differential operator which allows us to encode properties of the space under consideration. Quite remarkably, these methods lead us to a criterion for the Guillemin rigidity of a space in which neither this operator nor the theory of overdetermined partial differential equations appear. We apply this criterion to the Grassmannians of rank 2 and we determine all those which are rigid in the sense of Guillemin. In fact, we extend and complete our previous work on the real Grassmannians of rank 2 undertaken in [23]. Harmonic analysis on homogeneous spaces and results concerning the infinitesimal deformations of Einstein metrics also play an important role here.

In conjunction with the Blaschke conjecture, Michel had previously introduced another notion of rigidity for symmetric spaces; it coincides with Guillemin rigidity for spaces of rank one. We say that a symmetric p-form on an arbitrary symmetric space X satisfies the zero-energy condition if all its integrals over the closed geodesics of X vanish. The space X is said to be infinitesimally rigid if the only symmetric 2-forms on X satisfying the zero-energy condition are the Lie derivatives of the metric. The infinitesimal rigidity of a flat torus of dimension 2 was established by Michel in [46].

The canonical metric g of a projective space X equal to KPn, with n 2, or to the Cayley plane is a C-metric, i.e., a metric all of whose geodesics are closed and of the same length . An important question which arises from the Blaschke conjecture consists in determining whether the metric g is the only C-metric of X, up to an isometry. Green and Berger have answered this question in the affirmative in the case of the real projective spaces (see [5]). The infinitesimal deformation of g by Cmetrics satisfies the zero-energy condition. Thus the infinitesimal rigidity of X may be interpreted as the rigidity to first-order for the deformation problem of g by C-metrics. In [11], Duistermaat and Guillemin proved that a metric gon X, whose spectrum is equal to the spectrum of the metric g, is a C-metric. In the case of the real projective space RPn, with n 2, the positive resolution of the Blaschke conjecture then implies that the metric gis isometric to the metric g and, therefore, that this space is spectrally rigid. For the other projective spaces, which are not spheres, in [38] Kiyohara gave a partial answer to our question; in fact, he used the infinitesimal rigidity of X in order to show that a C-metric gon X, which is sufficiently close to g, is isometric to g. In all cases, Kiyohara’s work can be combined with the above-mentioned result of Duistermaat and Guillemin to give us the following spectral rigidity result: a metric gon X, whose spectrum is equal to that of g and which is sufficiently close to g, is isometric to g.

We now return to the study of the symmetric spaces of compact type of arbitrary rank. We show that a space which is rigid in the sense of Guillemin is also infinitesimally rigid. Thus Theorem 1 implies that the Grassmannian GK m,n, with m, n 1 and m = n, is infinitesimally rigid.

THEOREM 3 tells us that any Grassmannian, which is not isometric to a sphere, or to a product of spheres, or to , is infinitesimally rigid. The infinitesimal rigidity of such a Grassmannian, as long as it is not isometric to a projective space or to the Grassmannian , is proved by means of the methods used to demonstrate Theorem 1.

We now present the various methods for proving the Guillemin rigidity or the infinitesimal rigidity of an irreducible symmetric space of compact type. The first one requires techniques based on the harmonic analysis on homogeneous spaces of compact Lie groups. We used it in [14] to establish the infinitesimal rigidity of the complex projective space with n 2, and in [23] to prove the Guillemin rigidity of the Grassmannian The proofs of the infinitesimal rigidity of the complex quadric Q3 of dimension three, given in Chapter VI, and of the Grassmannian given in Chapter X, are similar in nature.

In [13], the theory of linear overdetermined partial differential equations of [28] is used to construct the resolution of the sheaf of Killing vector fields on a symmetric space. This resolution plays a fundamental role in our study of rigidity; in particular, one of its differential operators can be used to encode properties of families of totally geodesic submanifolds of our space and the prior knowledge of the rigidity of these submanifolds.

One approach to infinitesimal rigidity, which appears in [18], relies on a resolution of the sheaf of Killing vector fields and leads to a new proof of the infinitesimal rigidity of the complex projective space with n 2. For this space, this approach requires a minimal use of harmonic analysis; it also allows us to deduce the infinitesimal rigidity of the complex quadric with n 5, from that of its totally geodesic submanifolds isometric to the complex projective plane or to a flat 2-torus.

In Section 8 of Chapter II, we introduce a new approach to our rigidity problems which is partially inspired by the one developed in [22] for the study of the complex quadric of dimension four. We give criteria both for the Guillemin rigidity and for the infinitesimal rigidity of an irreducible space X of compact type which exploit the fact that X is an Einstein manifold. The relationship between the resolution of the sheaf of Killing vector fields and the finite-dimensional space E(X) of infinitesimal Einstein deformations of X introduced by Berger and Ebin [3] provides us with one of the main ingredients of the proofs of these criteria. We still require some results from harmonic analysis in the proofs of these criteria, but only in a limited way. Also the fact that the Lichnerowicz Laplacian acting on the space of symmetric forms is equal to a Casimir operator, which was proved by Koiso in [41], plays an important role. Although the theory of overdetermined partial differential equations enters in an essential way into the proofs of our criteria, it should again be emphasized that it does not appear in any form in their final statements.

We apply our criteria to the Grassmannians of rank 2 in order to prove Theorems 1 and 3 for these spaces. On such a Grassmannian which is equal to its adjoint space, the injectivity of the Radon transform for functions on the real projective plane is used to prove that the Guillemin condition is hereditary with respect to certain totally geodesic submani-folds. For our proofs, we also require the Guillemin rigidity of complex projective plane and the real Grassmannian Moreover, in the case of the complex Grassmannians, we must show that an infinitesimal Einstein deformation satisfying the Guillemin condition vanishes. This last fact, which is always a necessary condition for Guillemin rigidity, is proved in Chapter VIII for the Grassmannians with m n, by computing the integrals of specific symmetric 2-forms over certain closed geodesics.

In Chapters VII and VIII, we introduce an averaging process which assigns to a symmetric p-form on the space G

with n 2 and or C, a class of symmetric p-forms on the space This process has the following property, which enables it to play an essential role in the proof of Theorem 2: if the p-form u on G

satisfies the Guillemin condition, so do all the p-forms on associated to In fact, this process is used to show that an infinitesimal Einstein deformation of the complex Grassmannian satisfying the Guillemin condition vanishes. This last assertion and several others concerning the spaces are proved by induction on . To demonstrate Theorem 2, we also exploit to a considerable extent the methods which enter into the proofs of our rigidity criteria of Chapter II.

The study of 1-forms on the Grassmannians satisfying the Guillemin condition is of independent interest. Clearly, an exact 1-form always satisfies this condition. In fact, we have the following converse:

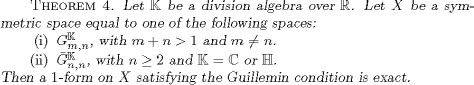
By means of our methods, we are able to give elementary and direct proofs of Grinberg’s result concerning the maximal flat Radon transform for functions on all the irreducible symmetric spaces of compact type considered above that are equal to their adjoint spaces.

In this monograph, all the known results concerning our rigidity problems for symmetric spaces, which are either of compact type, or flat tori, or products of such manifolds, are presented in a unified way. For the irreducible spaces, we give proofs which either are complete or omit only certain technical details.

We wish to point out that, in Chapters I and III, several results and formulas of Riemannian geometry are presented or derived in a particularly simple way. Moreover, the result concerning conformal Killing vector fields on Einstein manifolds given by Proposition 1.6 is new; it is required for the proof of Proposition 2.16. The latter proposition leads us to the necessary condition for Guillemin rigidity of an irreducible symmetric space described above.

We now proceed to give a brief description of the contents of the chapters of this monograph. In Chapter I, we introduce various differential operators on a Riemannian manifold (X, g) arising from the curvature and a complex of differential operators related to the Killing vector fields, which includes the differential operator mentioned above. When X is a compact Einstein manifold, the space E(X) of infinitesimal Einstein deformations of the metric g contains the cohomology of this complex. In [41] and [42], Koiso determined the irreducible symmetric spaces X of compact type for which the space E(X) vanishes; this result gives us the exactness of this complex for these spaces. The study of the Radon transforms, the tools derived from harmonic analysis on symmetric spaces and our criteria for rigidity are to be found in Chapter II. In the following chapter, we present the infinitesimal rigidity results for flat tori and the projective spaces, which are not equal to spheres. In particular, in the case of the real projective spaces, we give the proof of their infinitesimal rigidity due to Bourguignon (see [5]) and a variant of the one due to Michel [45].

In Chapter VII, we give the proofs of the rigidity of the real Grass-mannians of rank 3 and introduce the averaging process for symmetric forms on which leads to the result given by Theorem 2 for the adjoint spaces . In Chapter VIII, we study the differential geometry of the complex Grassmannians and we view them as symmetric spaces and homogeneous spaces. We introduce certain explicit functions and symmetric 2-forms on these spaces, which enter into our analysis of the space of infinitesimal Einstein deformations of these Grassmannians. We also define the averaging process for symmetric forms on the Grassmannian which is used here to prove properties of its space of infinitesimal Einstein deformations and in the next chapter to study the rigidity of its adjoint space Chapter IX is mainly devoted to the proofs of the rigidity of the complex and the quaternionic Grassmannians of rank 2.

In Chapter X, we prove the non-rigidity of the product of irreducible symmetric spaces, which we mentioned above. We also present results from [19] concerning the geometry of products of symmetric spaces and their infinitesimal rigidity. The study of the real Grassmannian is to be found here.