CHAPTER III

SYMMETRIC SPACES OF RANK ONE

1. Flat tori

Let (X, g) be a flat Riemannian manifold of dimension n. We first suppose that X is the circle S1 of length endowed with the Riemannian metric where t is the canonical coordinate of S1 defined modulo L. It is easily seen that this space X is infinitesimally rigid and that a 1-form on X satisfies the zero-energy condition if and only if it is exact.

In this section, we henceforth suppose that n 2. We recall that that the operator D1 is equal to Dg, and that the sequence (1.50) is exact. Let h be a section of over an open subset of X. According to formulas (1.20) and (1.21), we see that is equal to the section of B and that

In the remainder of this section, we suppose that (X, g) is a flat torus of dimension 2. We may consider X as the quotient of the space endowed with the Euclidean metric g0. In fact, there is a lattice generated by a basis such that X is equal to the quotient We shall identify a tensor on X with the -invariant tensor on which it determines. Clearly, a tensor on which is invariant under the group of all translations of induces a tensor on X. Let be the standard coordinate system of In particular, for the vector field and the 1-form dxj on are invariant under the group of all translations of and therefore induce a parallel vector field and a parallel 1-form on X, which we shall denote by j and j , respectively. Clearly,

where the coefficients and are real numbers. Hence the space of all parallel sections of (resp. of over X is isomorphic to the space of all differential forms of degree k (resp. of all symmetric p-forms) on with constant coefficients. In particular, the metric g is equal to the symmetric 2-form Since the cohomology group is isomorphic to , where x is an arbitrary point of X, we know that the space of harmonic forms of degree k on X is equal to the space of all parallel sections of over X.

PROPOSITION 3.1. Let X be a flat torus of dimension 2. Let be a vector field on X. Then is a Killing vector field if and only if

PROOF: We consider the 1-for on X. First, we suppose that X is a flat torus of dimension 2 and we consider the volume form = of X. According to formula (1.4), the 1-form satisfies the relations and Since a harmonic 1-form on X is parallel, we may write

Y From the first of the preceding equations, we infer that the function f on

2 can be written in the form f where fj is a real-valued function on depending only on xj . Then the second equality tells us that the function f1 - f2 on is harmonic and so is constant. It follows that the two functions f1 and f2 are also constant, and so the 1-form and the vector field are parallel. Now, we assume that the dimension of X is 2. Let x0 be a point of X and let 1 and be parallel vector fields on X; then there is a totally geodesic flat 2-torus Y of X containing x0 such that the vectors an 2(x0) are tangent to Y . We consider the vector fiel on Y , whose value at x is equal to the orthogonal projection of onto the subspace of Tx. If is the natural imbedding and is the Riemannian metric on Y induced by g, according to Lemma 1.1 we have and we know that is a Killing vector field on Y . Therefore the 1-form on Y is parallel. Since i is a totally geodesic imbedding, it follows that

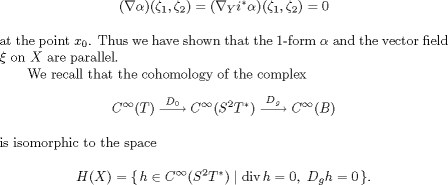
PROPOSITION 3.2. Let X be a flat torus of dimension 2. Let h be a symmetric 2-form on X. Then the following assertions are equivalent:

(i) We have h = 0.

(ii) We have h = 0.

(iii) The section h belongs to H(X).

PROOF: Let , be parallel vector fields on X. If f is the real-valued function on X equal to according to formula (1.52), we obtain the relation

Therefore if h vanishes, the function f is constant; since the parallel vector fields and are arbitrary, we see that vanishes. If h is a parallel section of according to (3.1) we see that Dgh = 0, and so h belongs to H(X). Finally, suppose that (iii) holds. Then according to (3.3), we see that Tr h therefore Tr h is constant. Formula (3.2) now tells us that

From Proposition 3.2, it follows that the space H(X) is equal to the space

of all parallel sections of According to remarks made in 3, Chapter I, we know that the cohomology group is isomorphic to this space, and therefore also to the vector space where x is an arbitrary point of X; thus the dimension of this cohomology group is equal to n(n + 1)/2. Other proofs of these results are given in [2] and [15] (see Proposition 17.1 of [15]). From Proposition 3.2 and the decomposition (1.11), it follows that an element h of satisfying Dgh = 0 can be written in the form

where is a vector field on X and h0 is a parallel section of over X.

LEMMA 3.3. Let u be a parallel symmetric p-form on a flat torus X of dimension 2. If the form u satisfies the zero-energy condition, then it vanishes.

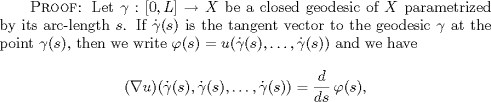
for all 0 s L. Our hypothesis tells us that the function on [0,L] is constant. If u over the interval [0,L] vanishes, and hence the expression vanishes for all L. If x is a point of X, we know that the set Cx of vectors of Tx - {0}, for which is a closed geodesic of X, is a dense subset of Tx. From these last two observations, we obtain the desired result.

LEMMA 3.4. Let h be a symmetric 2-form and u be a 1-form on a flat torus X of dimension 2 which satisfy the zero-energy condition.

(i) If the symmetric 2-form h satisfies the relation Dgh = 0, then it is a Lie derivative of the metric.

(ii) If the 1-form u satisfies the relation du = 0, then it is exact.

PROOF: We first suppose that the relation Dgh = 0 holds. As we saw above, we have the decomposition (3.4), where is a vector field on X and h0 is a parallel symmetric 2-form on X. According to Lemma 2.6, the form h0 also satisfies the zero-energy condition. From Lemma 3.3 with p = 2, we infer that h0 vanishes, and so the equality holds. If the 1-form is closed, then we may write

where f is a real-valued function on X and is a harmonic 1-form on X. Clearly, also satisfies the zero-energy condition. We saw above that is parallel; hence by Lemma 3.3 with p = 1, we see that is equal to df.

on is tangent to the line segment u. If is a symmetric p-form on X and is the -invariant symmetric p-form determined by , then the integral of over the closed geodesic of X is given by

where the constant depends only on the integers p, p1 and p2 and the basis {1, 2} of R

2.

The following proposition is due to Michel [46].

PROPOSITION 3.5. The X-ray transform for functions on a flat torus of dimension n 2 is injective.

PROOF: We first suppose that n = 2. Let f be a complex-valued function on X satisfying the zero-energy condition; we also denote by f the -invariant function on which it determines. We consider the Fourier series

of the function f on where the are its Fourier coefficients. We now fix a pair of integers (p1, p2); we suppose that and we consider the closed geodesic of X, which we associated above with the integers p1 and p2 and with the real number . We then consider the function on whose value at is equal to the integral of over the closed geodesic , where c0 is the constant appearing in the equality (3.5), with p = 0; according to our hypothesis, the function vanishes identically. Therefore the sum

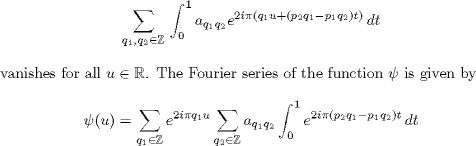
for Since the Fourier coefficient of corresponding to the integer p1 vanishes, we see that = 0. A similar argument shows that the coefficient vanishes when p1 = 0 and Thus the function f is constant and therefore vanishes. Since an arbitrary point of a flat torus of dimension 2 is contained in a totally geodesic flat torus of dimension 2, we obtain the desired result in all cases.

PROPOSITION 3.6. Suppose that X is a flat torus of dimension 2. Let h be a symmetric 2-form and be a 1-form on X; suppose that these two forms satisfy the zero-energy condition. Then we have the relations Dgh = 0 and = 0.

PROOF: We consider the -invariant symmetric forms

on determined by h and , where a, b, c, a1, a2 are -invariant functions on We now fix a pair of integers (p1, p2); we suppose that and we consider the closed geodesic of X which we associated above with the integers p1 and p2 and with the real number u. We consider the functions and on whose values at are equal to the integrals of / and h/c2 over the closed geodesi respectively; here cp is the constant appearing in the equality (3.5). According to our hypotheses, the functions and vanish identically. The Fourier series of the function is given by

respectively. Since is a frame for the tangent bundle of we see that Dgh = 0 and

THEOREM 3.7. A flat torus of dimension 2 is infinitesimally rigid.

THEOREM 3.8. A differential form of degree 1 on a flat torus of dimension 2 satisfies the zero-energy condition if and only if it is exact.

We now simultaneously prove Theorems 3.7 and 3.8. Let h be a symmetric 2-form and be a 1-form on the flat torus X, both of which satisfy the zero-energy condition. Let x be an arbitrary point of X and be an orthonormal set of vectors of Tx. If F is the subspace of Tx, then Y = ExpxF is a closed totally geodesic submanifold of X isometric to a flat 2-torus. Let be the natural imbedding; the forms and Y satisfy the zero-energy condition. If gY is the metric on Y induced by g, Proposition 3.6 tells us that DgY and According to Proposition 1.14,(i), the restriction of the section Dgh of B to Y vanishes. Hence we have

Thus these equalities holds for all and we see that Dgh = 0 and . According to Lemma 3.4, the symmetric form h on X is Lie derivative of the metric and the 1-form is exact.

THEOREMS 3.7 and 3.8 are due to Michel [46]; our proofs of these theorems are essentially the same as those given by Estezet [12]. The next theorem, which generalizes both of these theorems, was proved by Michel [46] when the integer p is equal to 0, 1 or an odd integer and by Estezet [12] in all the other cases.

PROOF: We consider the vector field on Y , whose value at is equal to the orthogonal projection of (x) onto the subspace of Tx.

According to Lemma 1.1, we have and we know that YYis a Killing vector field on Y . Therefore by Proposition 3.1, we see that and so the 1-form on Y is harmonic. Thus we have If satisfies the zero-energy condition, then so does the 1-form on Y ; by Theorem 3.8, the 1-form on the flat torus Y is exact and therefore vanishes.

2. The projective spaces

THEOREM 3.11. A symmetric space of rank one, which is not isometric to a sphere, is infinitesimally rigid.

THEOREM 3.12. Let X be a symmetric space of rank one, which is not isometric to a sphere. A differential form of degree 1 on X satisfies the zero-energy condition if and only if it is exact.

Most of the results described in the remainder of this section are to be found in Chapter 3 of [5]. Let n be an integer 1. Let be one of the fields We set We endow with its right vector space structure over with the Hermitian scalar product

We endow the sphere with the Riemannian metric induced by the scalar product (3.7), and the projective space with the Rie-mannian metric g determined by

(i) We have u, v= 0.

(ii) The vector is orthogonal to the subspace with respect to the metric g.

(iii) The subspaces and are orthogonal with respect to the metric g.

If are non-zero vectors of such that the subspaces are mutually orthogonal, then we have the decomposition

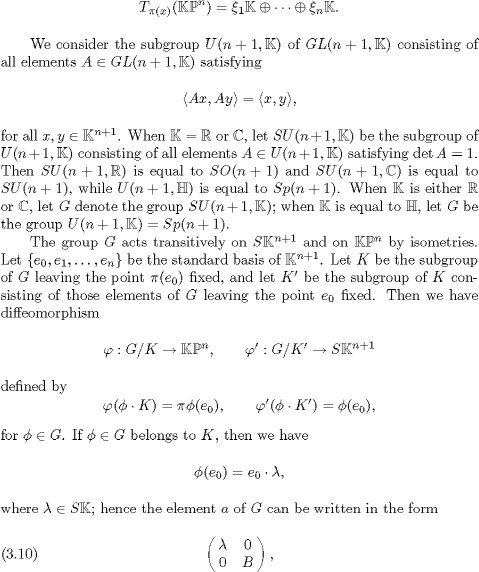
When in the remainder of this section we suppose that n 2. If In denotes the unit matrix of order n, the element

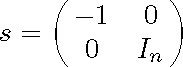
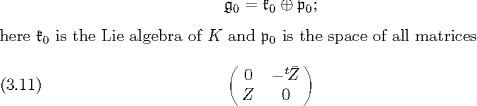
of where is viewed as a column vector and ^t is its conjugate transpose. We identify p0 with the vector space and, in particular, the element (3.11) of p0 with the vector Z of The adjoint action of K on p0 is expressed by

where is the element (3.10) of K and When we know that is also the Lie algebra of

The following result is proved in D of [5, Chapter 3].

The following result is a direct consequence of Proposition 3.14.

In G of [5, Chapter 3], the structure of symmetric space of rank one is defined on the Cayley plane X. An analogue of Proposition 3.14 holds for the Cayley plane. In fact, the inclusion of the quaternions H into the Cayley algebra gives rise to closed totally geodesic submanifolds of X isometric to HP2.

3. The real projective space

Let be the complexification of the Lie algebra of G = SO(n+1) and let be the dual of the group G. Let and be the elements of which are the equivalence classes of the trivial G-module and of the irreducible G-module respectively.

We view the sphere X = Sn = as the irreducible symmetric space SO(n + 1)/SO(n). The set of eigenvalues of the Laplacian acting on consists of all the integers where k is an integer 0. The eigenspace of associated with the eigenvalue consists of all the complex-valued functions on X which are restrictions to Sn of harmonic polynomials of degree k on According to observations made in 7, Chapter II and by Proposition 2.1, we know that Hk is an irreducible SO(n + 1)-submodule of and that the direct sum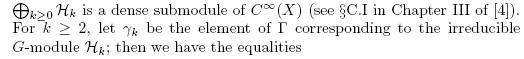

Let Y be the real projective space endowed with the metric which we view as an irreducible symmetric space. According to 7, Chapter II and the isomorphism (2.19), we see that the set of eigenvalues of the Laplacian acting on consists of all the integers 2k, with k 0; moreover if k is an even integer, the G-module is equal to the space of functions on Y obtained from Hk by passage to the quotient. Therefore is a dense subspace of and the first non-zero eigenvalue of the Laplacian acting on is equal to 2(n + 1).

We consider the closed geodesic of Sn, which is the great circle defined by

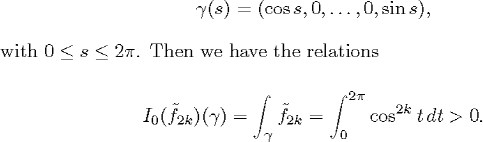
The following result is a consequence of the above observations and Proposition 2.29, with

PROPOSITION 3.17. An even function on the sphere Sn, with n 2, whose X-ray transform vanishes, vanishes identically.

In Chapter II, we noted that the preceding proposition is equivalent to assertion (i) of Theorem 2.23 and also that it implies that the X-ray transform for functions is injective on the real projective space with

Theorem 3.18. The X-ray transform for functions on a symmetric space of compact type of rank one, which is not isometric to a sphere, is injective.

PROOF: According to Proposition 3.14 and the discussion which follows this proposition, each point of such a projective space X is contained in a closed totally geodesic submanifold of X isometric to the projective plane The desired result is then a consequence of Theorem 2.23,(ii).

THEOREM 3.18, together with Proposition 2.26, implies that the X-ray transform for functions on a symmetric space X of compact type is injective if and only if X is not isometric to a sphere. Theorem 3.18 is also a consequence of Theorem 2.24.

We shall now establish the infinitesimal rigidity of the real projective space a result due to Michel [45]. We first consider the case of the real projective plane.

PROPOSITION 3.19. The real projective plane is infinitesimally rigid.

PROOF: Let h be a symmetric 2-form on X satisfying the zero-energy condition. We know that the relation (1.64) holds on the sphere which is a covering space of X; therefore we may write

where is a vector field and f is a realvalued function on X. I is closed geodesic of X

Since the Lie derivative satisfies the zero-energy condition, we see that the function f also satisfies the zero-energy condition. From Theorem 2.23,(ii), with n = 2, we deduce that the function f vanishes and so we have h

THEOREM 3.20. The real projective space X with n 2, is infinitesimally rigid.

Thus this last equality holds for all and we see that Dgh = 0. According to Theorem 1.18, the sequence (1.51) is exact, and so h is a Lie derivative of the metric.

The proof of Proposition 3.19 given above is due to Bourguignon and our proof of Theorem 3.20 is inspired by the one given in Chapter 5 of [5]. We now present a variant of the version given in [30, 2] of Michel’s original proof of Proposition 3.19 (see [45]).

We suppose that (X, g) is the real projective plane Let be an arbitrary closed geodesic parametrized by its arc-length. We set and let be the tangent vector to the geodesic at , for 0 t . We choose a unit vector orthogonal to e1(0) and consider the family of tangent vectors with obtained by parallel transport of the vector e2 along . Clearly, if u is an element of , we have

for the first equality holds because div h = 0, while the second one is obtained using the expression for the curvature of (X, g). The lemma is now a consequence of (3.12).

LEMMA 3.23. Let X be the real projective plane If h satisfies div h = 0, then

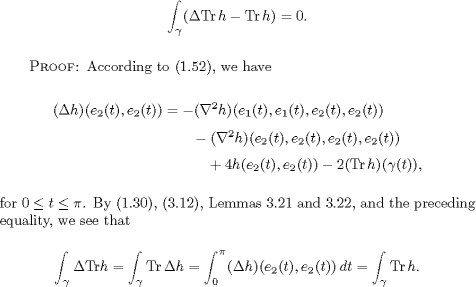
LEMMA 3.24. Let X be the real projective plane If h satisfies div h = 0, then Tr h vanishes.

PROOF: According to Theorem 2.23,(ii), with n = 2, and Lemma 3.23, we see that As the first non-zero eigenvalue of the Laplacian acting on is equal to 6, we see that Tr h = 0.

LEMMA 3.25. Let X be the real projective plane An element h of satisfying div h = 0 vanishes.

PROOF: Let h be an element of satisfying div h = 0. According to Lemma 3.24 and the equality (1.53), the symmetric 2-form h belongs to H(X). Then Proposition 1.20 tells us that h vanishes.

Now Proposition 3.19 is a direct consequence of Proposition 2.13 and Lemma 3.25.

Our approach to the rigidity questions, which led us to the criteria of Theorem 2.49 and the methods introduced in [22] for the study of the complex quadrics, were partially inspired by the proof of the infinitesimal rigidity of the real projective plane which we have just completed. The correspondence between the arguments given here in the case of the real projective plane and those used in the case of the complex quadric is pointed out in [30].

The following result is due to Michel [47].

THEOREM 3.26. A differential form of degree 1 on the real projective space , with n 2, satisfies the zero-energy condition if and only if it is exact.

In the case of the real projective plane according to Proposition 2.20, we see that Theorem 3.26 is a consequence of Proposition 3.29,(ii), which is proved below; on the other hand, the proof of this theorem given in [47] for is elementary and requires only Stokes’s theorem for functions in the plane. In fact, the result given by Theorem 3.26 for the real projective plane implies the result in the general case. Let X be the real projective space , with n 2; by Proposition 3.14, we easily see that an element of which vanishes when restricted to the totally geodesic surfaces of X isometric to the real projective plane, must be equal to 0. Then the desired result for X is a consequence of Proposition 2.51,(ii).

The following result due to Bailey and Eastwood [1] generalizes both Theorems 3.20 and 3.26.

In the case p = 2, the assertion of Theorem 3.27 was first established by Estezet (see [12] and [29]).

4. The complex projective space

In this section, we suppose that X is the complex projective space with n 1, endowed with the metric g of 2. We have seen that g is the Fubini-Study metric of constant holomorphic curvature 4. We denote by J the complex structure of X. As in 2, we identify X with the Hermi-tian symmetric space G/K, where G is the group SU(n + 1) and K is its subgroup S(U(n) × U(1)).

× The curvature tensor Rof X is given by

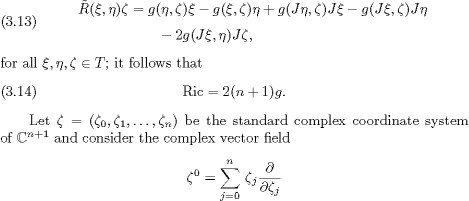
Let be the complexification of the Lie algebra of K. The group of all diagonal matrices of G is a maximal torus of G and of K. The complexification t of the Lie algebra of this torus is a Cartan subalgebra of the semi-simple Lie algebra g and also of the reductive Lie algebra For 0 the linear form sending the diagonal matrix with a0, a1, . . . , an as its diagonal entries into aj , is purely imaginary on Then

Then we see that highest weight of the irreducible G-module Hk is equal to and that is a highest weight vector of this module. Clearly, we have

The fibers of the homogeneous vector bundles and T0,1 at the point of X considered in 2 are irreducible K-modules of highest weights equal to and respectively. According to the branching law for G and K (see Proposition 3.1 of [14]), from the results of [14, 4] we obtain the following:

PROPOSITION 3.28. Let X be the complex projective space with n 1.

For the remainder of this section, we suppose that n = 1 and that We consider the sphere S2 = the mapping

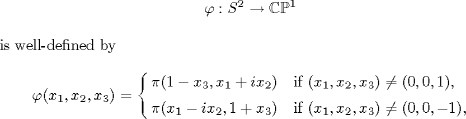
where (x1, x2, x3) R3, with x21 + x22 + x23 = 1. The two expressions for correspond to the stereographic projections whose poles are the points (0, 0, 1) and (0, 0,-1), respectively, and so we know that is a diffeomor-phism. We also consider the involution of which sends the point of CP1, where u is a non-zero vector of into the point where v is a non-zero vector of orthogonal to u. I is the anti-podal involution of the sphere S2, it is easily verified that the diagram

Since Hk is an irreducible G-module which contains the function f

by (3.27) we see that

According to the commutativity of diagram (3.25), the first assertion of the next proposition is equivalent to the result concerning the sphere S2 given by Proposition 3.17; moreover according to Proposition 2.20, the second assertion of the next proposition implies the result concerning the real projective plane stated in Theorem 3.26.

PROPOSITION 3.29. Let X be the complex projective space .

(i) An even function on X, whose X-ray transform vanishes, vanishes identically.

(ii) An even differential form of degree 1 on X satisfies the zero-energy condition if and only if it is exact.

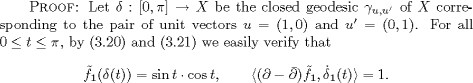
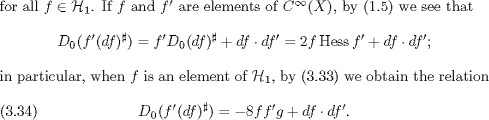
5. The rigidity of the complex projective space

We now introduce various families of closed connected totally geodesic submanifolds of X. Let x be a point of X, and let be the family of all closed connected totally geodesic surfaces of X passing through x of the form ExpxF, where F is the subspace of the tangent space Tx generated by an orthonormal set of vectors of Tx satisfying Let F2,x be the family of all closed connected totally geodesic surfaces of X passing through x of the form ExpxF, where F is the subspace of the tangent space Tx determined by a unitary vectror of Tx. We consider the G-invariant families

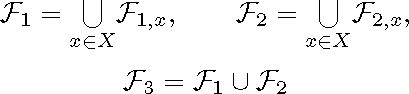
of closed connected totally geodesic surfaces of X.

According to Proposition 3.14, a surface belonging to the family F1 is isometric to the real projective plane with its metric of constant curvature 1, while a surface belonging to the family F2 is isometric to the complex projective line with its metric of constant curvature 4.

For j = 1, 2, 3, we consider the sub-bundle of B consisting of those elements of B which vanish when restricted to the submanifolds of Fj . An element u of B belongs to N1 if and only if the relation

LEMMA 3.34. Let h be an element of belonging to Then we have D1h = 0.

PROOF: By Lemma 3.33, we know that h also belongs to Hence by Proposition 2.45, with F = F3, we see that By Proposition 3.31, we therefore know that D1h = 0.

The equivalence of assertions (i) and (iii) of the following theorem is originally due to Michel [45]. We now provide an alternate proof of Michel’s result following [13, 8].

THEOREM 3.35. Let h be a symmetric 2-form on with n 2. The following assertions are equivalent:

(i) The symmetric 2-form h belongs to

(ii) We have D1h = 0.

(iii) The symmetric 2-form h is a Lie derivative of the metric g.

LEMMA 3.37. Let X be the complex projective space with n 2. The following assertions are equivalent:

(i) The space X is infinitesimally rigid.

(ii) (3.37)

(ii) The complex (3.37) is exact.

LEMMA 3.38. A real-valued function f on X satisfies if and only if it vanishes identically.

PROOF: Let f be a real-valued function f on X satisfying According to Lemma 3.36, the symmetric 2-form fg satisfies the zero-energy condition, and so the X-ray transform of f vanishes. From Theorem 3.18, we obtain the vanishing of f.

Since 2n is not an eigenvalue of , it follows that f vanishes identically. In fact, according to Lichnerowicz’s theorem (see [43, p. 135] or Theorem D.I.1 in Chapter III of [4]) and (3.14), we see that the first non-zero eigenvalue of is > 2(n + 1); we have also seen that the first non-zero eigenvalue of is equal to 4(n + 1).

The following theorem gives us the infinitesimal rigidity of the complex projective spaces of dimension 2.

THEOREM 3.39. The complex projective space with n 2, is infinitesimally rigid.

The infinitesimal rigidity of the complex projective spaces of dimension 2 was first proved by Tsukamoto [53]; in fact, he first proved directly the infinitesimal rigidity of and then used the above-mentioned result of Michel given by Theorem 3.35 to derive the rigidity of the complex projective spaces of dimension > 2. Other proofs of Theorem 3.39 may be found in [14] and [18].

We can also obtain the infinitesimal rigidity of the complex projective spaces of dimension 2 from the rigidity of the complex projective plane by means of Theorem 2.47. In fact, we apply this theorem to the family F equal to F3 and to the family consisting of all closed totally geodesic submanifolds of X isometric to according to Propositions 3.14, 3.31 and 3.32, we know that the hypotheses of Theorem 2.47 hold.

We remark that the equivalence of assertions (i) and (iii) of Theorem 3.35 may be obtained from Theorem 3.39 and Lemma 3.33 without requiring Propositions 3.31 and 3.32.

We now present an outline of the proof of Theorem 3.39 given in [14]. Since the differential operator is homogeneous and the differential operator D0 is elliptic, according to Lemma 3.37 and Proposition 2.3 we see that the space X is infinitesimally rigid if and only if the complex

is exact for all .

We choose a Cartan subalgebra of and fix a system of positive roots of . If is an arbitrary element of , we determine the multiplicities of the G-modules and and then describe an explicit basis for the weight subspace Wof corresponding to its highest weight in terms of elements of the eigenspaces Hk; either the multiplicity of C(S2TC) is equal to 4 and the multiplicity of is equal to 2, or these two multiplicities are 2. Since X is an irreducible Hermitian symmetric space, according to (2.28) the multiplicity of the G-module is equal to 2. The multiplicity of is also equal to 2; in fact, we show that

Before proceeding to the description of another proof of Theorem 3.39 given in [18], we shall prove the following result which first appeared in [17].

THEOREM 3.40. A differential form of degree 1 on with n 2, satisfies the zero-energy condition if and only if it is exact.

PROOF: Let F be the sub-bundle of consisting of those elements of which vanish when restricted to the submanifolds of F1. An element of belongs to F if and only if the relation

holds for all vectors satisfying An elementary algebraic computation shows that F is the line bundle generated by the form of X. Let be a differential form of degree 1 on X. Since any closed geodesic of X is contained in a submanifold belonging to the family F1, we see that the 1-form satisfies the zero-energy condition if and only if the restrictions of to the submanifolds belonging to the family F1 satisfy the zero-energy condition. According to Theorem 3.26, the latter property of holds if and only if is a section of F. We now suppose that the 1-form satisfies the zero-energy condition; our previous observations imply that satisfies the relation

where f is a real-valued function on X. From this equality, we infer that

and so f is constant. Since the is harmonic, the function f vanishes and so the form is closed; hence is exact.

The simplicity of the preceding proof, which is based on a remark of Demailly (see [18]), rests on the correct interpretation of the bundle F. This observation led us to a new proof of the infinitesimal rigidity of , which can be found in [18] and which requires a minimal amount of harmonic analysis. For symmetric 2-forms, the analogue of the bundle F of the preceding proof is the bundle N1, and its interpretation is given by Proposition 3.30.

We now describe the proof of Theorem 3.39 given in [18]. We consider the first-order differential operator introduced in 3, Chapter I. Clearly, if u is a section of B satisfying = 0, from the definition of we infer that D1u = 0. The following two results are proved in [18].

LEMMA 3.41. Let be a section of the bundle over an open subset of X satisfying

Then the 2-form is closed.

for all integers k > 1. This inequality is verified in the appendix of [18].

Let h be a symmetric 2-form on X satisfying the zero-energy condition.

B From Proposition 3.19, it follows that h belongs to the space By Proposition 2.44 or Lemma 1.15, we see that D1h is a section of N1/. Thus by Proposition 3.30, there exists a section of over X such that

Then Lemma 1.17 tells us that the equality (3.40) holds; hence according to Lemma 3.41, the 2-form is closed. Therefore there exists a constant and a real-valued function f on X such that

Since is parallel, we know that Hence the equality (3.40) implies that By Lemma 3.42, the function f belongs to . Therefore without loss of generality, we may assume that the function f belongs to H₁.

We consider the subspaces

Thus by Proposition 3.30, we see that Dg(f1g) is a section of N1. Then Lemma 3.38 tells us that the function f1 vanishes identically. Therefore D1halso vanishes, and so D1h = 0. By Proposition 3.32 and Theorem 1.18, the complex (1.24) is exact, and so h is a Lie derivative of the metric.

6. The other projective spaces

Let X be a projective space equal either to the quaternionic projective space with n 2, or to the Cayley plane. Let F1 be the family of all closed connected totally geodesic surfaces of X which are isometric either to the real projective plane with its metric of constant curvature 1 or to the sphere S2 with its metric of constant curvature 4. Let F2 be the family of all closed connected totally geodesic submanifolds of X isometric to the projective plane We verify that every surface belonging to the family F1 is contained in a submanifold belonging to the family F2 (see Proposition 3.14, [45, 3.2] and [17, 3]).

We consider the sub-bundle N = NF1 of B consisting of those elements of B which vanish when restricted to the submanifolds of F1. The following proposition can be proved by means of computations similar to the ones used in [14] to prove Proposition 3.31 and the relation (3.36) for the complex projective spaces.

PROPOSITION 3.43. Let X be equal to the quaternionic projective space with n 2, or to the Cayley plane. Then we have

We remark that the equalities of the preceding proposition imply that the relation (1.48) holds for the space X. Thus we may apply Theorem 2.47 to the families F1 and F2 in order to obtain the following result from the infinitesimal rigidity of

Theorem 3.44. The quaternionic projective space with n 2, and the Cayley plane are infinitesimally rigid.

Theorem 3.45. Let X be equal to the quaternionic projective space with n 2, or to the Cayley plane. A differential form of degree 1 on X satisfies the zero-energy condition if and only if it is exact.

PROOF: According to Propositions 3.14 and 3.15 (see Corollary 3.26 of [5]) when X is equal to a quaternionic projective space, or by observations made in [17, 3] when X is the Cayley plane, we easily see that

By Theorem 3.40, we know that the hypotheses of Theorem 2.51 are satisfied. The latter theorem now gives us the desired result.

Let be the family of all closed connected totally geodesic submani-folds of X isometric to the projective line (which is a sphere of dimension 4), or to the projective line over the Cayley algebra (which is a sphere of dimension 8), as the case may be. By means of the methods which we used in 5 to prove Theorem 3.35 for the complex projective spaces, we may also derive the following theorem, which is weaker than Theorem 3.44.

THEOREM 3.46. Let X be equal to the quaternionic projective space with n 2, or to the Cayley plane. If h is a symmetric 2-form on X, the following assertions are equivalent:

(i) The symmetric 2-form h belongs to (

(ii) We have D1h = 0.

(iii) The symmetric 2-form h is a Lie derivative of the metric g.

The equivalence of assertions (i) and (iii) of Theorem 3.46 were first proved by Michel (see [45]). In [53], Tsukamoto deduced the infinitesimal rigidity of X from this result of Michel, the infinitesimal rigidity of and the exactness of sequence (1.51) for the sphere of dimension 2; he requires the equality (1.57) of Proposition 1.14,(i) and uses an argument similar to the one appearing in the proof of Theorem 3.20.