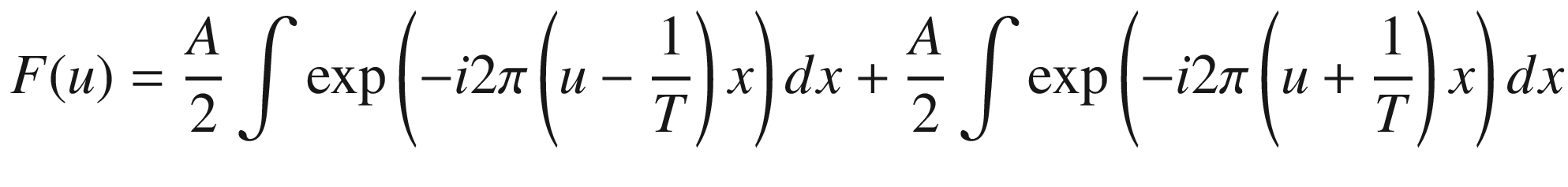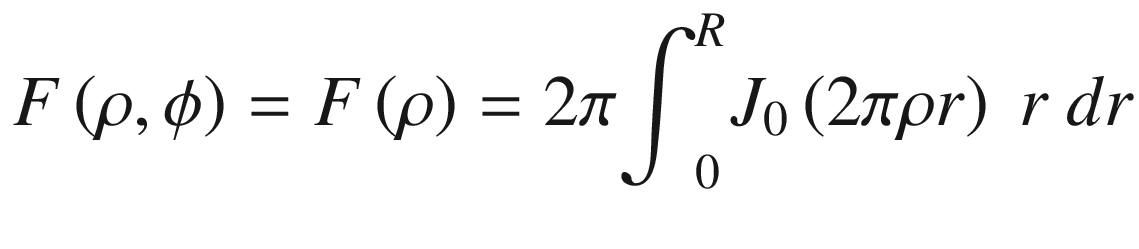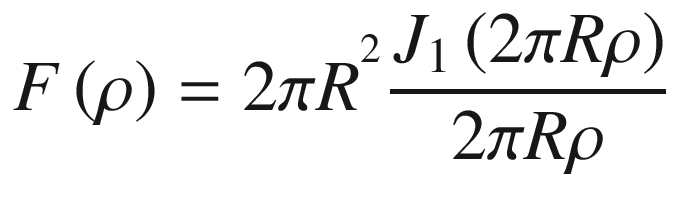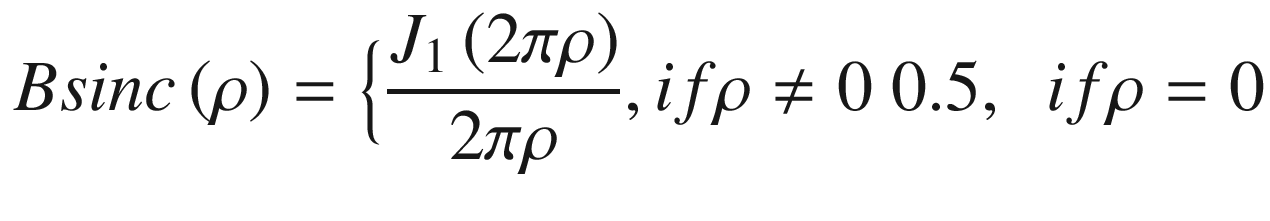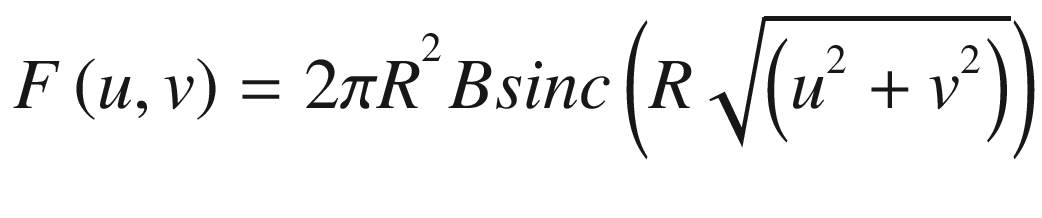© The Author(s), under exclusive license to APress Media, LLC, part of Springer Nature 2021
M. Cywiak, D. CywiakMulti-Platform Graphics Programming with Kivyhttps://doi.org/10.1007/978-1-4842-7113-1_17

17. Two-Dimensional Fourier Transform

Moisés Cywiak1   and David Cywiak2
(1)
Leon, Guanajuato, Mexico
(2)
Queretaro, Mexico
 
In this chapter, we present elements for calculating and plotting discrete two-dimensional Fourier transforms. Figure 17-1 provides two screenshots from an Android cell phone. The one on the left shows a rectangular, two-dimensional spatial-function. The right screenshot shows the corresponding discrete Fourier transform obtained using this program.
../images/510726_1_En_17_Chapter/510726_1_En_17_Fig1_HTML.png
Figure 17-1

Screenshots from an Android cell phone showing a two-dimensional spatial-function (left) and its corresponding Fourier transform obtained with this program (right)

The functionality of Button1 to Button8 is the same as described in Chapter 5.

In this application, Button9 toggles the numerical indicator between 0 and 1. Accordingly, the screen shows the spatial function or its corresponding two-dimensional Fourier transform.

17.1 One-Dimensional Fourier Transform

Briefly speaking, the Fourier transform consists of an integral that transforms a function defined in an initial domain into another function in the frequency domain. The initial domain can be any n-dimensional space of interest.

The Fourier transform is frequently used in digital processing, probability, optics, quantum mechanics, economics, and many other fields. The transform can be one-, two-, three-, or n-dimensional.

Let’s start by writing the following analytical expression for the one-dimensional Fourier transform:
$$ F(u)={int}_{-infty}^{infty }f(x) mathit{exp}left(-i2pi ux ight) dx $$
(17.1)

In Equation (17.1), the function in the initial domain is f(x), and the transformed function in the frequency domain is F(u). The parameter i represents the imaginary unit. The initial domain is represented by the spatial x-coordinate and the frequency coordinate is represented by u.

To verify that u in Equation (17.1) represents frequency, let’s consider that f(x) is a sinusoidal function with period T and amplitude A:
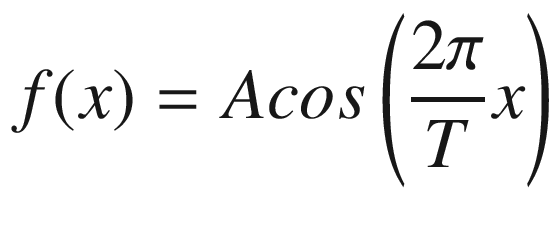
$$ f(x)= Acosleft(frac{2pi }{T}x ight) $$
(17.2)
To calculate the Fourier transform of the function in the initial space given by Equation (17.2), we use Euler’s identity to rewrite the equation as follows:
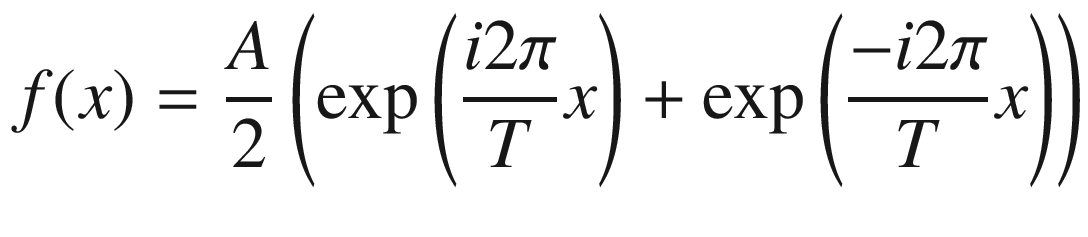
$$ f(x)=frac{A}{2}left(mathit{exp}left(frac{i2pi }{T}x ight)+mathit{exp}left(frac{-i2pi }{T}x ight) ight) $$
(17.3)
Substituting Equation (17.3) into Equation (17.1) gives us the following:
$$ F(u)=frac{A}{2}int mathit{exp}left(-i2pi left(u-frac{1}{T} ight)x ight) dx+frac{A}{2}int mathit{exp}left(-i2pi left(u+frac{1}{T} ight)x ight) dx $$
(17.4)
The integrals in Equation (17.4) are precisely the definitions of the Dirac delta function. Therefore, Equation (17.4) gives the following:
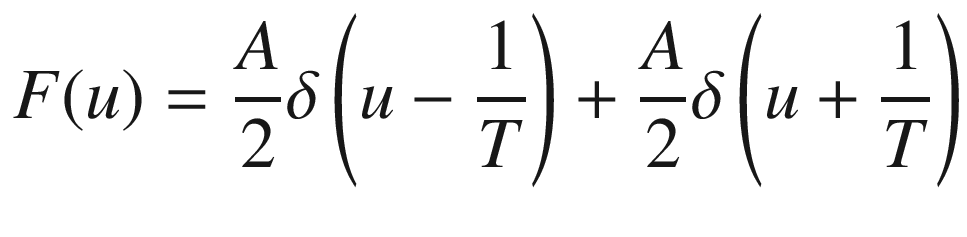
$$ F(u)=frac{A}{2}delta left(u-frac{1}{T} ight)+frac{A}{2}delta left(u+frac{1}{T} ight) $$
(17.5)

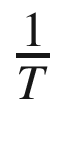A physical interpretation of Equation (17.5) consists of visualizing f(x) in Equation (17.2) as a vibrating string placed along the horizontal x-coordinate. The string vibrates vertically with a period equal to T, or equivalently with a frequency $$ frac{1}{T} $$. Then, Equation (17.5) indicates that the Fourier transform, F(u), consists of two well defined points in the frequency domain located at $$ frac{1}{T} $$ and $$ frac{-1}{T} $$. We conclude, therefore, that when a string vibrates at a determined frequency, the Fourier transform consists of two points. The first one corresponds to the vibration frequency. The second, to the negative value of this frequency.

To proceed further with this interpretation of the Fourier transform, we now consider that the string in our previous example vibrates at two different frequencies, with amplitudes A1and A2, as follows:
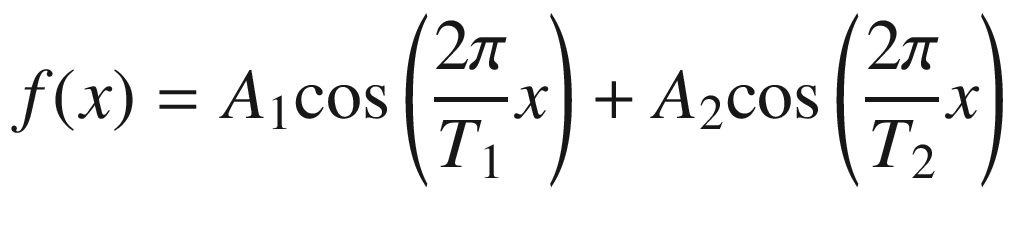
$$ f(x)={A}_1mathit{cos}left(frac{2pi }{T_1}x ight)+{A}_2mathit{cos}left(frac{2pi }{T_2}x ight) $$
(17.6)
As in the last example, using Euler’s identity for each sinusoidal function allows us to calculate the Fourier transform of the expression given in Equation (17.6), as follows:
$$ F(u)=left[frac{A_1}{2}delta left(u-frac{1}{T_1} ight)+frac{A_1}{2}delta left(u+frac{1}{T_1} ight) ight]+left[frac{A_2}{2}delta left(u-frac{1}{T_2} ight)+frac{A_1}{2}delta left(u+frac{1}{T_2} ight) ight] $$
(17.7)

From Equation (17.7), we notice that the Fourier transform consists of two well-defined points for each vibrating frequency . Each point corresponds to the positive or negative value of a frequency. Each point in the frequency space has an amplitude equal to half of its corresponding one.

Considering that the string vibrates at multiple frequencies, each frequency with a corresponding amplitude, the Fourier transform will give points at all the frequencies of vibration, including positives and negatives, along with their corresponding half amplitude values. Therefore, the Fourier transform provides the amplitude distribution of frequencies of a vibrating object and its spectral distribution.

In the following section, we introduce two functions frequently encountered in Fourier analysis.

17.2 The Rectangular and Sinc Functions

Two functions of special interest in Fourier studies are the Rect(x, A) (rectangular) and the sinc(x) functions.

The rectangular function is a rectangle of height 1 and width A. Analytically:
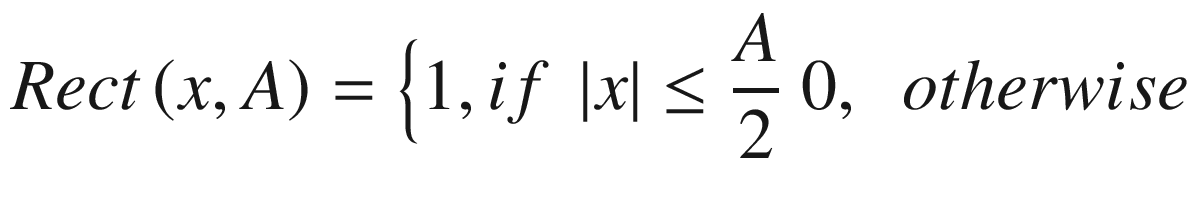
$$ Rectleft(x,A ight)=Big{1, if left|x ight|le frac{A}{2} 0,kern0.5em otherwise $$
(17.8)
Figure 17-2 depicts the rectangular function given by Equation (17.8).
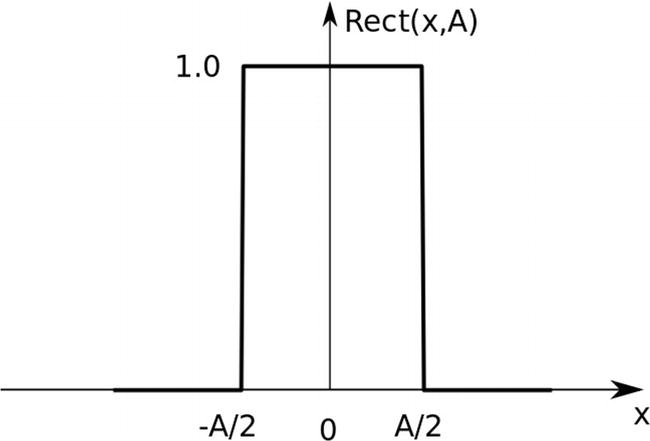
../images/510726_1_En_17_Chapter/510726_1_En_17_Fig2_HTML.jpg
Figure 17-2

The Rect(x, A) Function

The Fourier transform of Equation (17.8) reads as follows:
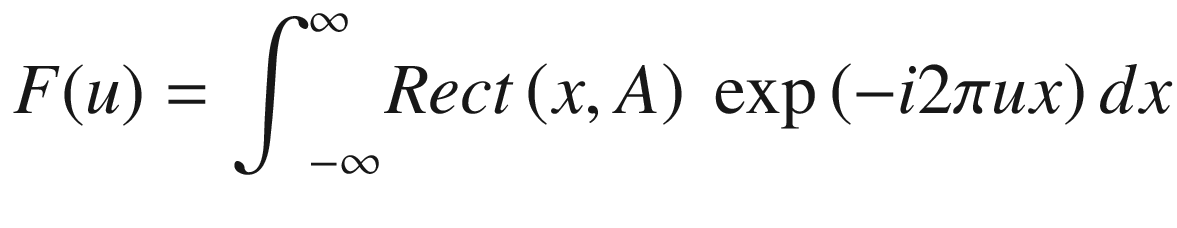
$$ F(u)={int}_{-infty}^{infty } Rectleft(x,A ight) mathit{exp}left(-i2pi ux ight) dx $$
(17.9)
To calculate the integral in Equation (17.9), we substitute Equation (17.8) into Equation (17.9):
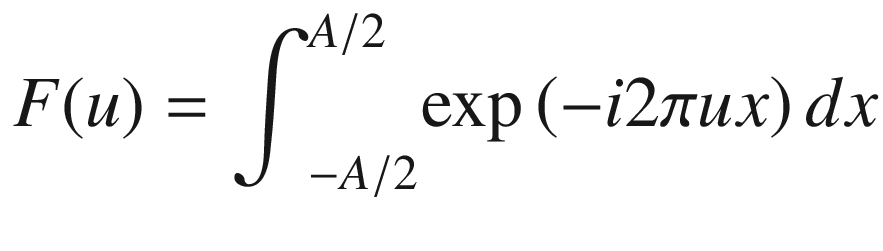
$$ F(u)={int}_{-A/2}^{A/2}mathit{exp}left(-i2pi ux ight) dx $$
(17.10)
Performing the integral of Equation (17.10) gives the following:
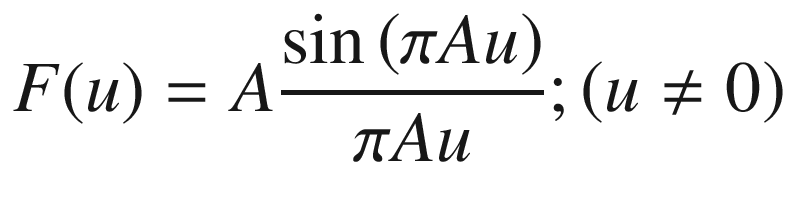
$$ F(u)=Afrac{mathit{sin}left(pi Au ight)}{pi Au};left(u e 0 ight) $$
(17.11)
The frequency domain for F(u), as expressed by Equation (17.11), is valid from −∞ to ∞, except when u equals zero, where the expression becomes undefined. This drawback is overcome by assigning to the function the value corresponding to the limit when u → 0. Therefore, sinc(u) is defined as follows:
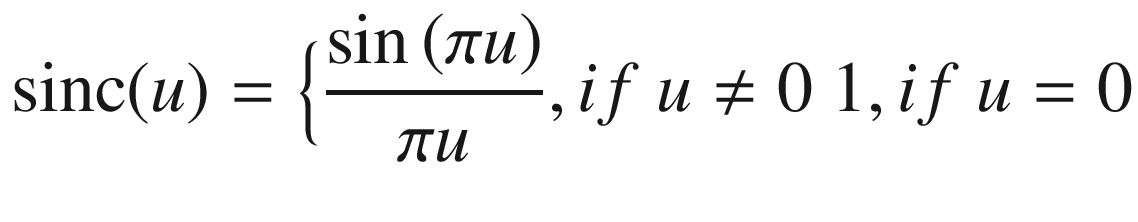
$$ mathit{operatorname{sinc}}(u)=Big{frac{mathit{sin}left(pi u ight)}{pi u}, if u e 0 1, if u=0 $$
(17.12)
Equation (17.12), scaled by and multiplied by factor A, is plotted in Figure 17-3.
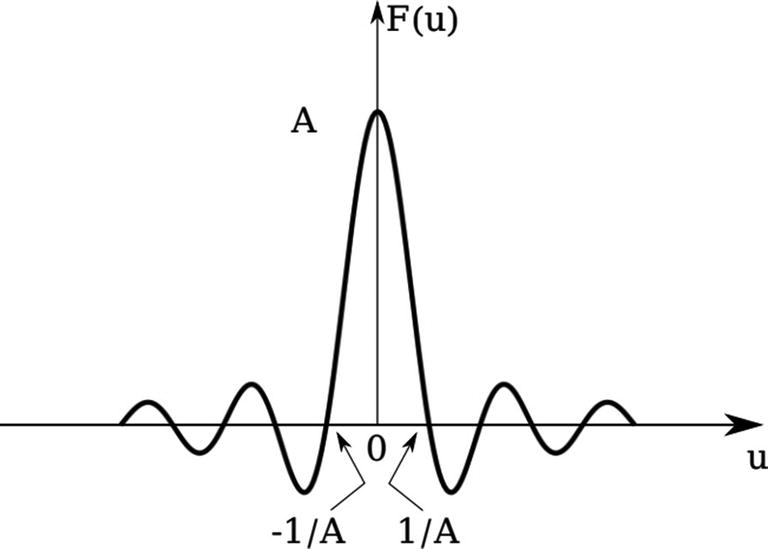
../images/510726_1_En_17_Chapter/510726_1_En_17_Fig3_HTML.jpg
Figure 17-3

Plot of Asinc(Au). Intercepts with the u-axis occur at $$ u=frac{pm 1}{A} $$

Although we want to focus on the two-dimensional Fourier transform, for illustrative purposes, we provide a brief code description for calculating the discrete one-dimensional Fourier transform in the next section.

17.3 Code for Calculating the Discrete One-Dimensional Fourier Transform

We need first to generate the spatial function. In the first working example, this function will be a two-dimensional rectangular function. We can obtain it as the product of two one-dimensional rectangles given by Equation (17.8). We will generate the one-dimensional Rect function using the code shown in Listing 17-1.
import numpy as np
def Rect(x,a):
    if (np.abs(x)<=A/2):
        return 1;
    else:
        return 0;
Listing 17-1

The Rect Function

Next, we set the number of pixels that will represent the discrete function.
N=200;

To better represent this function in the one-dimensional case, we can use a large number of pixels while keeping a short processing time. This is in contrast to the two-dimensional case, where a small N increment can result in very high processing times.

We now assign the values of the imaginary unit and π to the variables i and Pi, as follows.
i=1J;  Pi=np.pi;
Now, we will use two variables, L to set the x-range between (–L/2 to L/2), and A to define the width of the rectangular function, as follows:
L=1; A=L/2.4;

The width of the rectangle function was set to L/(2.4).

Next we create two one-dimensional arrays, each with size N+1, to store the values of the x-points and the values corresponding to the spatial function:
x=np.zeros(N+1);
f=np.zeros( N+1 );
Now we fill the arrays, as shown in Listing 17-2.
for n in range(0,N+1):
    x[n]=(n-N/2)/N*L
    f[n]=Rect(x[n],A);
Listing 17-2

Setting Values for x and f

In this for loop, we have assigned N+1 entries with values ranging from -L/2 to L/2 to the first array for storing the x-points. The N+1 values corresponding to the function are stored in the second array, f.

The following code creates the frequency array, as shown in Listing 17-3.
u=np.zeros(N+1);
B=10/A;
for n in range(0,N+1):
    u[n]=(n-N/2)/N*B;
Listing 17-3

Setting Frequency Values

In the for loop, the frequency (or spectral) array, u, stores N+1 equally spaced values ranging from -B/2 to B/2. The value 10/A assigned to the parameter B is set based in our experience when calculating the sinc function depicted in Figure 17-3.

Now we create an array to store the values of the Fourier transform as follows:
F=np.zeros( N+1, dtype=complex );

We have declared F as a one-dimensional array for storing N+1 complex numbers. This is necessary, as the calculations of the integral given by Equation (17.1) will give, in general, complex numbers.

At this point, u represents N+1 frequency points ranging from -B/2 to B/2. As a consequence, F(u) will be also represented by a discrete array, F.

We can use a discrete summation on the elements of f to approximate the integral of the Fourier transform, as follows:
$$ Fleft[n ight]={sum}_{m=0}^Nfleft[m ight] mathit{exp}left(-i2pi uleft[n ight]xleft[m ight] ight) dx $$
(17.13)

In Equation (17.13), dx is set to a positive value corresponding to the subtraction of two consecutive elements of the x-array as, for example, dx=x[1]-x[0].

We can calculate the discrete integral for each F[n] using the code shown in Listing 17-4.
for n in range(0,N+1):
    S=0;
    for m in range(0,N+1):
        S=S+ f[m]*np.exp(-i*2*Pi*u[n]*x[m]);
    F[n]=S;
Listing 17-4

Calculating the Discrete Integral

In this code, the inner for loop calculates the discrete integral corresponding to a particular F[n] entry, determined by the outer for loop. For each n iteration, the S parameter is set to 0, and it accumulates the value of the discrete integral. Once the inner for loop finishes, the F[n] parameter receives its corresponding value and the outer for loop continues. The process is repeated until all the F[n] values are filled.

Although this code for calculating the N+1 discrete integral works properly, it is not time-efficient. Fortunately, NumPy provides a time-efficient built-in function to perform the summation for each F[n]. When using NumPy, the summation looks as follows:
for n in range(0,N+1):
    F[n]=np.sum( f * np.exp(-i*2*Pi*u[n]*x) );

In this code, np.sum performs the appropriate summation by associating each element of the f array with its match in the x array. The arrays must be the same size.

By comparing the Fourier transforms obtained by these two examples, one can confirm that the examples give the same result.

The precision of the calculations depends on the discretization process and the accuracy of the computer’s mathematical processor. Therefore, although we have demonstrated that the Fourier transform of a real-valued rectangular function should be a real-valued function, the resulting values of F[n] will be complex numbers. For practical purposes, the imaginary values are negligible compared to their real ones. However, we have to explicitly discard the imaginary parts of F[n] and keep only the real parts. This is done by plotting np.real(F[n]).

In the following section, we focus on the two-dimensional Fourier transform.

17.4 Two-Dimensional Fourier Transform

The two-dimensional Fourier transform is defined as follows:
$$ Fleft(u,v ight)={int}_{-infty}^{infty }{int}_{-infty}^{infty }fleft(x,y ight) mathit{exp}left(-i2pi left( ux+ vy ight) ight) dx dy $$
(17.14)

In Equation (17.14), f(x, y) represents a two-dimensional spatial function and F(u, v) represents its corresponding Fourier transform. The u and v parameters are the corresponding frequencies for the x and y coordinates, respectively.

As a first example, we will consider a rectangular two-dimensional function, written as follows:
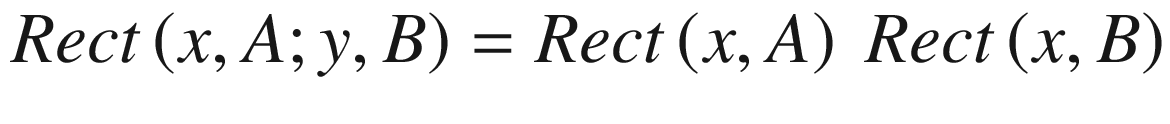
$$ Rectleft(x,A;y,B ight)= Rectleft(x,A ight) Rectleft(x,B ight) $$
(17.15)

The left plot of Figure 17-1 shows a screenshot of the program running on an Android cell phone with a plot of Equation (17.15).

The two-dimensional rectangular function in Equation (17.15) is separable in the x- and y-coordinates. However, as in general, not all the functions are separable. We will maintain our code as general as possible to permit calculations on non-separable f(x, y) functions. Furthermore, as we describe in the following section, to improve the processing time, we will write the two-dimensional transform given by Equation (17.14) as follows:
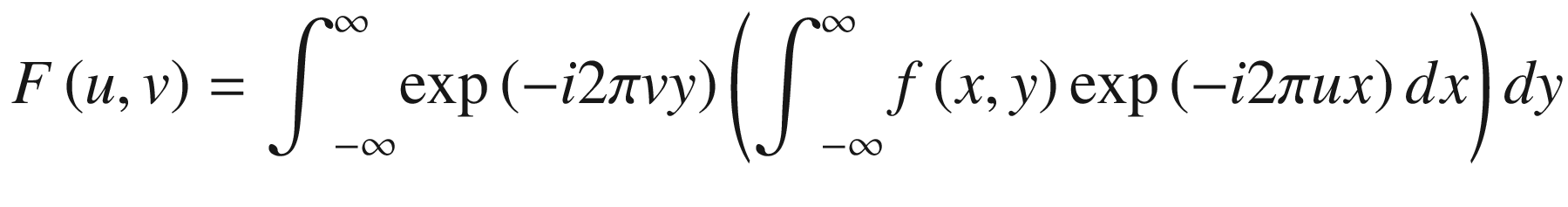
$$ Fleft(u,v ight)={int}_{-infty}^{infty}mathit{exp}left(-i2pi vy ight)left({int}_{-infty}^{infty }fleft(x,y ight)mathit{exp}left(-i2pi ux ight) dx ight) dy $$
(17.16)

Equation (17.16) allows us to calculate the Fourier transform of the two-dimensional function by performing an integration on the x-coordinate first and then an integration over the y-coordinate.

In the following section, we describe this method.

17.5 Discrete Two-Dimensional Fourier Transform

To numerically calculate the Fourier transform, we need to represent the continuous spatial function by a discrete set of numbers stored in a two-dimensional array. Therefore, we must use a moderate number of pixels for this task. As with the two-dimensional case, increasing this number will greatly increase the processing time.

We will use 40x40 pixels to represent the spatial function as well as the function in the frequency space. The x- and z-coordinates will be stored in independent one-dimensional arrays with N+1 entries. Next, we will create the mesh with two-dimensional (N+1)x(N+1) arrays. The corresponding code for creating the spatial function and mesh is shown in Listing 17-5.
import numpy as np
N=40; #Number of pixels to represent the function
# Creating spatial coordinates
x=np.zeros(N+1);
z=np.zeros(N+1);
f=np.zeros( (N+1,N+1) );
# Creating the mesh
x1=np.zeros( (N+1,N+1) );
y1=np.zeros( (N+1,N+1) );
z1=np.zeros( (N+1,N+1) );
L=1;
for n in range (0,N+1):
    x[n]=(n-N/2)/N*L;
    z[n]=(n-N/2)/N*L;
dx=x[1]-x[0]; dz=z[1]-z[0];
for n in range(0,N+1):
    for m in range(0,N+1):
        f[n][m]=Rect(x[n],L/2)*Rect(z[m],L/2);
Listing 17-5

Setting Values for the Mesh and the Discrete Spatial Function

In this code, we created the one-dimensional arrays x and z with their corresponding values. Using these arrays, we created the two-dimensional discrete function, f. We also defined the dx and dz variables to be used later in the integration.

We will also create corresponding arrays for the frequency parameters, as shown in Listing 17-6.
B=10/L; # Bandwidth
u=np.zeros(N+1); v=np.zeros(N+1);
#F will store the discrete Fourier transform
F=np.zeros( (N+1,N+1), dtype=complex );
for n in range(0,N+1):
    u[n]=(n-N/2)/N*B;
    v[n]=u[n];
Listing 17-6

Creating and Filling Frequency Parameters

The goal is now to perform the discrete double integral that corresponds to Equation (17.16), written as follows:
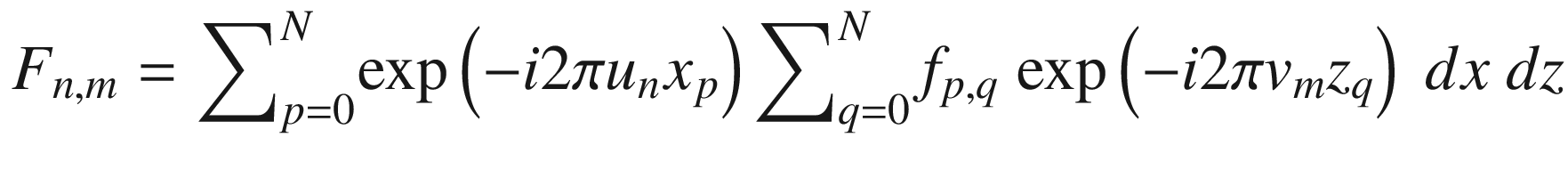
$$ {F}_{n,m}={sum}_{p=0}^Nmathit{exp}left(-i2pi {u}_n{x}_p ight){sum}_{q=0}^N{f}_{p,q} mathit{exp}left(-i2pi {v}_m{z}_q ight) dx dz $$
(17.17)
Equation (17.17), in terms of arrays, can be rewritten as follows:
$$ Fleft[n ight]left[m ight]={sum}_{p=0}^Nleft[mathit{exp}left(-i2pi uleft[n ight]xleft[p ight] ight){sum}_{q=0}^Nfleft[p ight]left[q ight]mathit{exp}left(-i2pi vleft[m ight]zleft[q ight] ight) ight] dx dz $$
(17.18)

Note that the summation operations in Equation (17.18) are not independent from each other. The second summation is inside the first one.

The code corresponding to the summation over q that corresponds to a determined p value can be written as follows:
S=0;
for q in range(0,N+1):
       S=S+ f[p][q]*np.exp(-i*2*Pi*v[m]*z[q]);

In the for loop, we are storing the result of the summation in the variable S. The S variable is an accumulator. It starts with a value equal to 0, and at each for loop, it accumulates the corresponding value. The for loop is set from 0 to N+1 because Python finishes the for loop when q equals N. Therefore, the summation goes from 0 to N, as required by Equation (17.18).

Now, as Equation (17.18) has a double summation, we need two accumulators. The corresponding code is shown in Listing 17-7.
for n in range(0,N+1):
    for m in range(0,N+1):
        S1=0;
        for p in range (0,N+1):
            S2=0;
            for q in range(0,N+1):
                if (f[p][q]==0):
                    continue;
                S2=S2+ f[p][q]*np.exp(-i*2*Pi*v[m]*z[q]);
            if (S2==0):
                continue;
            S1=S1+S2*np.exp(-i*2*Pi*u[n]*x[p]);
        F[n][m]=S1;
F=F*dx*dz;
Listing 17-7

Discrete Two-Dimensional Integral Using Two Accumulators

In this code, we included two if statements to avoid calculations when f[p][q] or S2 equals 0. These statements, which may seem irrelevant, reduced the processing time from 30 to 10 seconds in our dual-core computer running at 3.0GHz, for N=40.

The previous code can be improved by using the built-in numpy.sum function , as shown in Listing 17-8.
for n in range(0,N+1):
    for m in range(0,N+1):
        S=0;
        for q in range(0,N+1):
            S=S+np.sum( f[q]*
                np.exp(-i*2*Pi*u[n]*x) )
                       *np.exp(-i*2*Pi*v[m]*z[q] );
        F[n][m]=S;
F=F*dx*dz;
Listing 17-8

Method Using One-NumPy-Sum and One Accumulator

In this code, we only need one accumulator, as NumPy will sum f[q] and x as one-dimensional arrays, performing the corresponding inner summation of Equation (17.18). We still have to calculate the outer summation with the for loop over the variable q.

The processing time using this code in our dual-core computer took about three seconds. Compared to ten seconds with the previous code, this represents approximately one-third of the processing time. The summation of arrays made by NumPy, therefore, are highly efficient.

To use two NumPy summations and avoid using accumulators for calculating the double summation expressed by Equation (17.18), we devised the code shown in Listing 17-9.
C=np.zeros( (N+1,N+1), dtype=complex );
for n in range(0,N+1):
    for m in range(0,N+1):
        for q in range(0,N+1):
            C[n][q]=np.sum( f[q]
                        *np.exp(- i*2*Pi*u[n]*x) );
        F[n][m]=np.sum( C[n]*np.exp(-i*2*Pi*v[m]*z) );
F=F*dx*dz;
Listing 17-9

Method Using Double NumPy Summation by Introducing an Additional Array

In this code, we used the C array to store (N+1)x(N+1) complex values. With this approach, there is no need for accumulators, so we can use two NumPy summations to perform the required calculations. The processing time is one second.

This method is the most general, as it does not need separate functions in the integrals.

It is further possible to use double-NumPy summation without using the additional array, taking advantage of the exponential functions in the Fourier transform integral, as they are separable. This time we have to use an extra option of the built-in summation, specifying which axis of the double summation will be used. The code is shown in Listing 17-10.
for n in range(0,N+1):
    for m in range(0,N+1):
        F[n][m]= np.sum(  np.sum( f*np.exp(
                -i*2*Pi*v[m]*z),axis=1 )
                *np.exp(-i*2*Pi*u[n]*x), axis=0  );
F=F*dx*dz;
I=np.abs(F);
Listing 17-10

Method with Double NumPy Sum Avoiding the Use of an Additional Array

In this code, integration over z is performed first, and then integration over x. The processing time is now less than one second.

In the following listings, we provide the code listings corresponding to the main.py and File.kv files. We included two spatial functions—a two-dimensional rectangle expressed as the product of two rectangular functions given by Equation (17.8) and a circular function. The circular function has a vertical height equal of 1 inside a circle of radius R, and 0 outside it. Analytically, the circular function can be expressed as follows:
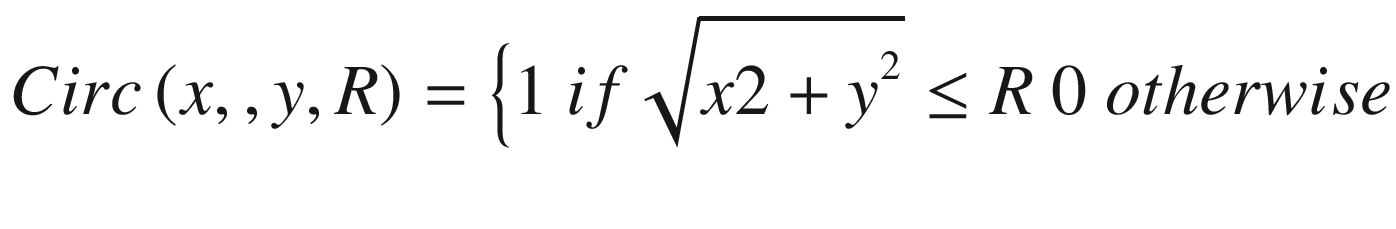
$$ Circleft(x,,y,R ight)=Big{1 ifsqrt{x2+{y}^{{}^2}}le R 0 otherwise $$
(17.19)
The code for main.py and File.kv are shown in Listings 17-11 and 17-12, respectively.
from kivy.app import App
from kivy.uix.floatlayout import FloatLayout
from kivy.graphics import Line, Ellipse, Color
from kivy.clock import Clock
import os
import numpy as np
from kivy.lang import Builder
Builder.load_file(
    os.path.join(os.path.dirname(os.path.abspath(
                            __file__)), 'File.kv')
                  );
#Avoid Form1 of being resizable
from kivy.config import Config
Config.set("graphics","resizable", False)
Config.set('graphics', 'width',  '480');
Config.set('graphics', 'height', '680');
#Here, we define two functions. We will use
#one of them in the calculations.
def Rect(s,a):
    if np.abs(s)<=a/2:
        return 1;
    else:
        return 0;
def Circ(s,t,a):
    if np.sqrt(s**2 +t**2)<=a:
        return 1;
    else:
        return 0;
OBJECT=0;
D=4000;
VX=600; VY=1200; VZ=0;
P=0.5
ZG0=P*D;
N=40; #Number of pixels to represent the function
# Creating spatial coordinates
x=np.zeros(N+1);
z=np.zeros(N+1);
f=np.zeros( (N+1,N+1) );
# Creating the mesh
x1=np.zeros( (N+1,N+1) );
y1=np.zeros( (N+1,N+1) );
z1=np.zeros( (N+1,N+1) );
L=1;
for n in range (0,N+1):
    x[n]=(n-N/2)/N*L;
    z[n]=(n-N/2)/N*L;
dx=x[1]-x[0]; dz=z[1]-z[0];
for n in range(0,N+1):
    for m in range(0,N+1):
        #Here we need to uncomment the
        #function we want to use:
        #Option (1) 2D Rect function:
        #f[n][m]=Rect(x[n],L/2)*Rect(z[m],L/2);
        #Option (2) 2D Circ function:
        f[n][m]=Circ(x[n],z[m],L/4);
Scale_x=140; Scale_y=100; Scale_z=140;
# Filling the mesh
for n in range (0,N+1):
    for m in range(0,N+1):
        x1[n][m]=Scale_x * x[n];
        z1[n][m]=Scale_z * z[m]+ZG0;
        y1[n][m]=Scale_y*f[n][m];
i=1J; # Defining imaginary unit
Pi=np.pi;
# Creating and filling frequency parameters
B=10/L;
u=np.zeros(N+1); v=np.zeros(N+1);
# F will store the discrete Fourier transform
F=np.zeros( (N+1,N+1), dtype=complex );
# C is used to calculate the discrete integral
C=np.zeros( (N+1,N+1), dtype=complex );
u1=np.zeros( (N+1,N+1) );
v1=np.zeros( (N+1,N+1) );
I1=np.zeros( (N+1,N+1) );
for n in range(0,N+1):
    u[n]=(n-N/2)/N*B;
    v[n]=u[n];
for n in range(0,N+1):
    for m in range(0,N+1):
        for q in range(0,N+1):
            C[n][q]=np.sum( f[q]
                          *np.exp(-i*2*Pi*u[n]*x) );
        F[n][m]=np.sum( C[n]
                    *np.exp(-i*2*Pi*v[m]*z) )*dx*dz;
# We will plot the absolute value of the
# discrete integral
I=np.abs(F);
# Creating the mesh for plotting
Scale_u1=15; Scale_v1=15; Scale_I1=480;
for n in range(0,N+1):
    for m in range(0,N+1):
        u1[n][m]=Scale_u1 * u[n];
        v1[n][m]=Scale_v1 * v[m]+ZG0;
        I1[n][m]=Scale_I1*I[n][m];
# Array to store list of points
PointList=np.zeros( (N+1,2) );
def GraphFunction(xM, yM, zM,  B):
    global N, D, VX, VY, VZ;
    x1p=xM; y1p=yM; z1p=zM;
    B.ids.Screen1.canvas.clear(); # Clear the screen
     # Choose color to draw
    B.ids.Screen1.canvas.add( Color(1,0,0) );
    # Drawing horizontal lines
    for n in range (0,N+1):
        for m in range (0,N+1):
            Factor=(D-VZ)/(D-z1p[n][m]-VZ);
            xA=XC+Factor*(x1p[n][m]-VX)
                                +VX+(P/(1-P))*VX;
            yA=YC+Factor*(y1p[n][m]-VY)
                                +VY+(P/(1-P))*VY;
            PointList[m]=xA,yA;
        B.ids.Screen1.canvas.add( Line(points=
                    PointList.tolist(), width=1.3));
    # Drawing vertical lines
    for n in range (0,N+1):
        for m in range (0,N+1, 1):
            Factor=(D-VZ)/(D-z1p[m][n]-VZ);
            xA=XC+Factor*(x1p[m][n]-VX)+VX
                                      +(P/(1-P))*VX;
            yA=YC+Factor*(y1p[m][n]-VY)+VY
                                      +(P/(1-P))*VY;
            PointList[m]=xA,yA;
        B.ids.Screen1.canvas.add( Line(points=
                    PointList.tolist(), width=1.3));
def RotateFunction(xM,yM,zM, B, Sense):
    global D, N;
    x1p=xM; y1p=yM; z1p=zM;
    if Sense==-1:
        Teta=np.pi/180*(-4.0);
    else:
        Teta=np.pi/180*(4.0);
    Cos_Teta=np.cos(Teta)
    Sin_Teta=np.sin(Teta);
    X0=0;  Y0=0;  Z0=ZG0 # Center of rotation
    for n in range(0,N+1):
        for m in range(0,N+1):
            if (B.ids.Button3.state=="down" or
                       B.ids.Button4.state=="down"):
                yP=(y1p[n][m]-Y0)*Cos_Teta  
                     + (x1p[n][m]-X0)*Sin_Teta + Y0;
                xP=-(y1p[n][m]-Y0)*Sin_Teta
                      +(x1p[n][m]-X0)*Cos_Teta + X0;
                y1p[n][m]=yP;
                x1p[n][m]=xP;
            if (B.ids.Button5.state=="down" or
                       B.ids.Button6.state=="down"):
                yP=(y1p[n][m]-Y0)*Cos_Teta
                     + (z1p[n][m]-Z0)*Sin_Teta + Y0;
                zP=-(y1p[n][m]-Y0)*Sin_Teta
                      +(z1p[n][m]-Z0)*Cos_Teta + Z0;
                y1p[n][m]=yP;
                z1p[n][m]=zP;
            if (B.ids.Button7.state=="down" or
                       B.ids.Button8.state=="down"):
                xP=(x1p[n][m]-X0)*Cos_Teta
                     + (z1p[n][m]-Z0)*Sin_Teta + X0;
                zP=-(x1p[n][m]-X0)*Sin_Teta
                      +(z1p[n][m]-Z0)*Cos_Teta + Z0;
                x1p[n][m]=xP;
                z1p[n][m]=zP;
class Form1(FloatLayout):
    def __init__(Handle, **kwargs):
        super(Form1, Handle).__init__(**kwargs);
        Event1=Clock.schedule_once(Handle.Initialize);
    def Initialize(B, *args):
        global W,H, XC,YC;
        W,H=B.ids.Screen1.size;
        XI,YI=B.ids.Screen1.pos
        XC=XI+int (W/2);
        YC=YI+int(H/2)-60;
    def Button1_Click(B):
        if (OBJECT==0):
            GraphFunction(x1,y1,z1,B);
        else:
            GraphFunction(u1,I1,v1, B);
    def Button2_Click(B):
        B.ids.Screen1.canvas.clear();
    def Button3_Click(B):
        if (OBJECT==0):
            RotateFunction(x1,y1,z1,B,1);
            GraphFunction(x1,y1,z1, B);
        else:
            RotateFunction(u1,I1,v1,B,1);
            GraphFunction(u1, I1,v1, B);
    def Button4_Click(B):
        if (OBJECT==0):
            RotateFunction(x1,y1,z1, B,-1),
            GraphFunction(x1,y1,z1, B);
        else:
            RotateFunction(u1,I1,v1,B,-1);
            GraphFunction(u1,I1, v1,B,);
    def Button5_Click(B):
        if (OBJECT==0):
            RotateFunction(x1,y1,z1,B,-1),
            GraphFunction(x1,y1,z1,B);
        else:
            RotateFunction(u1,I1,v1,B,-1);
            GraphFunction(u1,I1,v1,B);
    def Button6_Click(B):
        if (OBJECT==0):
            RotateFunction(x1,y1,z1,B,1),
            GraphFunction(x1,y1,z1,B);
        else:
            RotateFunction(u1,I1,v1,B,1);
            GraphFunction(u1,I1,v1,B);
    def Button7_Click(B):
        if (OBJECT==0):
            RotateFunction(x1,y1,z1,B,-1),
            GraphFunction(x1,y1,z1,B);
        else:
            RotateFunction(u1,I1,v1,B,-1);
            GraphFunction(u1,I1,v1,B);
    def Button8_Click(B):
        if (OBJECT==0):
            RotateFunction(x1,y1,z1,B,1),
            GraphFunction(x1,y1,z1,B);
        else:
            RotateFunction(u1,I1,v1,B,1);
            GraphFunction(u1,I1,v1, B);
    def Button9_Click(B):
        global OBJECT
        OBJECT=(OBJECT+1)%2;
        B.ids.Label1.text=str(OBJECT);
        B.ids.Screen1.canvas.clear();
        if (OBJECT==0):
            GraphFunction(x1,y1,z1,B);
        else:
            GraphFunction(u1,I1,v1,B);
# This is the Start Up code.
class StartUp (App):
    def build (BU):
        BU.title="Form1"
        return Form1();
if __name__ =="__main__":
    StartUp().run();
Listing 17-11

Code for the main.py File

#:set W 440
#:set H 440
<Form1>:
    id : Form1
    StencilView:
        id: Screen1
        size_hint: None,None
        pos_hint: {"x":0.04, "y":0.34}
        size: W,H
        canvas.before:
            Color:
                rgba: 0.9, 0.9, 0, 1
            RoundedRectangle:
                pos:  self.pos
                size: self.size
    Button:
        id: Button1
        on_press: Form1.Button1_Click()
        text: "Button1"
        size_hint: None,None
        pos_hint: {"x": 0.2, "y":0.03}
        size: 100,30
    Button:
        id: Button2
        on_press: Form1.Button2_Click()
        text: "Button2"
        size_hint: None,None
        pos_hint: {"x": 0.63, "y":0.03}
        size: 100,30
    Button:
        id: Button3
        on_press: Form1.Button3_Click()
        text: "Button3"
        size_hint: None,None
        pos_hint: {"x": 0.05, "y":0.12}
        size: 100,30
        always_release: True
    Button:
        id: Button4
        on_press: Form1.Button4_Click()
        text: "Button4"
        size_hint: None,None
        pos_hint: {"x": 0.73, "y":0.12}
        size: 100,30
    Button:
        id: Button5
        on_press: Form1.Button5_Click()
        text: "Button5"
        size_hint: None,None
        pos_hint: {"x": 0.05, "y":0.20}
        size: 100,30
    Button:
        id: Button6
        on_press: Form1.Button6_Click()
        text: "Button6"
        size_hint: None,None
        pos_hint: {"x": 0.73, "y":0.20}
        size: 100,30
    Button:
        id: Button7
        on_press: Form1.Button7_Click()
        text: "Button7"
        size_hint: None,None
        pos_hint: {"x": 0.05, "y":0.28}
        size: 100,30
    Button:
        id: Button8
        on_press: Form1.Button8_Click()
        text: "Button8"
        size_hint: None,None
        pos_hint: {"x": 0.73, "y":0.28}
        size: 100,30
    Button:
        id: Button9
        on_press: Form1.Button9_Click()
        text: "Button9"
        size_hint: None,None
        pos_hint: {"x": 0.4, "y":0.12}
        size: 100,30
    Label:
        id: Label1
        text: "0"
        font_size: 30
        color: 1,1,0,1
        size_hint: None,None
        pos_hint: {"x": 0.38, "y":0.20}
        size: 100,30
Listing 17-12

Code for the file.kv File

17.6 The Fourier Transform of the Circular Function

Figure 17-4 shows plots of the circular function and its corresponding absolute value of the discrete Fourier transform obtained with the code in this chapter.
../images/510726_1_En_17_Chapter/510726_1_En_17_Fig4_HTML.jpg
Figure 17-4

Plots of the circular function and its corresponding absolute value of the discrete Fourier transform obtained with this chapter’s code

As with the rectangular function, the Fourier transform of the circular function has an exact analytical expression in terms of a Bessel function of the first kind. In the following section, we provide a brief demonstration of this aspect.

17.7 Fourier Transform of the Circular Function

The Fourier transform of the circular function of the previous section can be expressed by an exact analytical equation. We will begin by expressing the Fourier transform given by Equation (17.14) in cylindrical coordinates. For this purpose, we express the spatial coordinates as follows:
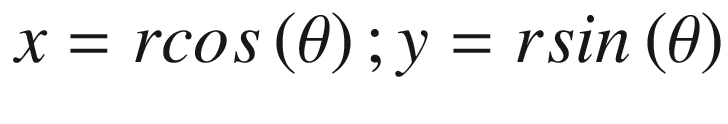
$$ x= rcosleft( heta ight);y= rsinleft( heta ight) $$
(17.20)
Similarly, we express the frequency coordinates as follows:
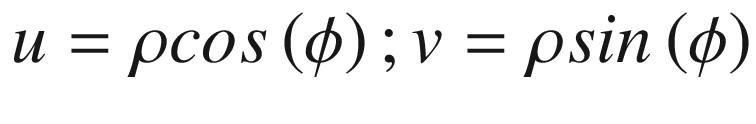
$$ u= ho cosleft(phi ight);v= ho sinleft(phi ight) $$
(17.21)
Substituting Equations (17.20) and (17.21) into the Fourier transform integral given by Equation (17.14) gives the following:
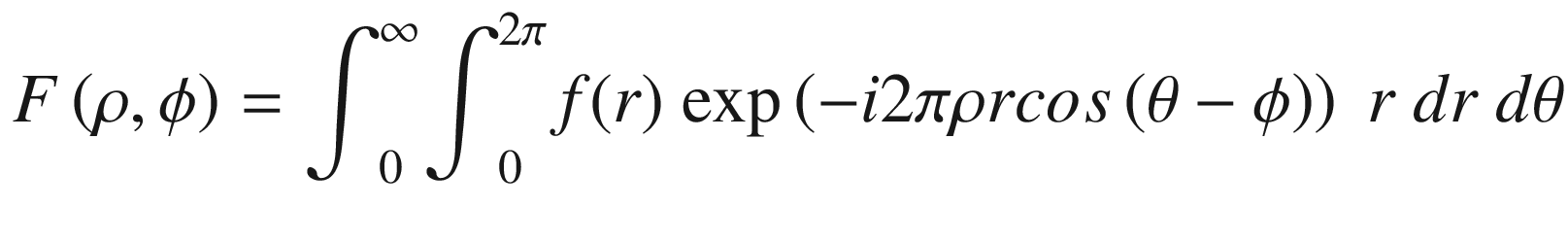
$$ Fleft( ho, phi ight)={int}_0^{infty }{int}_0^{2pi }f(r) mathit{exp}left(-i2pi ho rcosleft( heta -phi ight) ight) r d r d heta $$
(17.22)

In writing Equation (17.22), we substituted f(x, y) with f(r). The limits 0 to infinity will also be substituted with 0 to R, because of the circular function with radius R.

The integral over θ can be performed by using the following relation:
$$ {int}_0^{2pi}mathit{exp}left(left(- ixcosleft( heta -phi ight) ight) ight) d heta =2pi {J}_0(x) $$
(17.23)

In Equation (17.23), J0 is the Bessel function of the first kind, order zero.

Substituting Equation (17.23) into Equation (17.22) gives the following:
$$ Fleft( ho, phi ight)=Fleft( ho ight)=2pi {int}_0^R{J}_0left(2pi ho r ight) r dr $$
(17.24)

As indicated by Equation (17.24), the Fourier transform becomes a function only of ρ, because the integral in Equation (17.23) eliminates the ϕ dependence.

Using the change of variable, s = 2πρr, in Equation (17.24) gives the following:
$$ Fleft( ho ight)=frac{2pi }{{left(2pi ho ight)}^2}{int}_0^{2pi ho R}{J}_0(s) s ds $$
(17.25)
The integral in Equation (17.25) can be calculated by using the following identity:
$$ {left.{int}_0^x{J}_0(s) ds=s{J}_1(s) ight|}_0^x=x{J}_1(x) $$
(17.26)

In Equation (17.26), J1(x) is the Bessel function of the first kind, order one.

By using Equation (17.26) in Equation (17.25), we obtain the following:
$$ Fleft( ho ight)=2{pi R}^{{}^2}frac{J_1left(2pi R ho ight)}{2pi R ho} $$
(17.27)
Based on Equation (17.27), we define the Bessel-sinc function, referred to as Bsinc:
$$ Bsincleft( ho ight)=Big{frac{J_1left(2pi ho ight)}{2pi ho}, if ho e 0 0.5,kern0.5em if ho =0 $$
(17.28)

In Equation (17.28), we assigned the value of 0.5 to the function at ρ = 0 according to the following limit:

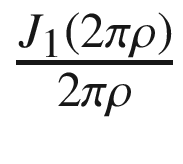$$ frac{J_1left(2pi ho ight)}{2pi ho} $$ =0.5 (17.29)

Using the definition given by Equation (17.28) in Equation (17.27) results in:
$$ Fleft( ho ight)=2{pi R}^{{}^2} Bsincleft( R ho ight) $$
(17.30)
In Equation (17.30), $$ ho =sqrt{left({u}^{{}^2}+{v}^{{}^2} ight)} $$, therefore:
$$ Fleft(u,v ight)=2{pi R}^{{}^2} Bsincleft(Rsqrt{left({u}^{{}^2}+{v}^{{}^2} ight)} ight) $$
(17.31)
Equation (17.31) is the appropriate expression to compare with the discrete Fourier transform obtained with this program. The code shown in Listing 17-13 uses SymPy to generate F(u, v).
import sympy as sp
def Bsinc(s):
    if (s!=0):
        return ( sp.besselj(1,s) )/s;
    else:
        return 0.5;
FP=np.zeros( (N+1,N+1), dtype=complex );
IP1=np.zeros( (N+1,N+1) );
R=L/4;
for n in range(0,N+1):
    for m in range(0,N+1):
        rho=np.sqrt( u[n]**2 +v[m]**2 )
        FP[n][m]=(2*Pi* R**2 )*Bsinc( 2*Pi*R*rho );
IP=np.abs(FP);
for n in range(0,N+1):
    for m in range(0,N+1):
        IP1[n][m]=Scale_I1*IP[n][m];
Listing 17-13

Generating the Discrete Function F(u, v)

Now we can plot the function using the following:
GraphFunction(u1,IP1,v1,B);
Figure 17-5 shows a plot of the absolute values corresponding to the discrete Fourier transform (left) and a plot of the analytical solution given by Equation (17.30) (right).
../images/510726_1_En_17_Chapter/510726_1_En_17_Fig5_HTML.jpg
Figure 17-5

Absolute values for the discrete Fourier transform (left) and of the analytical solution from Equation (17.30) (right)

Comparing the plots in Figure 17-5 confirms that the calculations performed with the code corresponding to the discrete two-dimensional Fourier transform results in an accurate estimate of the two-dimensional analytical Fourier transform.

In the following chapter, we extend this method to plot stereoscopic two-dimensional Fourier transforms.

17.8 Summary

In this chapter, we presented elements for calculating and plotting discrete two-dimensional Fourier transforms. The chapter included brief analytical descriptions of the one- and two-dimensional Fourier transforms. We provided working examples for calculating the corresponding transforms. To enhance the flexibility of the calculations in the two-dimensional case, we introduced three methods for calculating the discrete double integrals, allowing us to compare their efficiency and applicability.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
18.188.175.182