In a graph of friends connected to each other, an interesting question to ask is who the most influential person in the group is. Is it the person with the most connections, that is, the vertex with the highest degree? For directed graphs, in-degree might be a good first guess. Or is it rather the person who knows a selected few people who themselves have a lot of connections? There are certainly many ways to describe how important or authoritative a vertex is and the concrete answer will depend on the problem domain a lot, as well as on what additional data we are given with the graph. Moreover, in the example we have given, for a specific person in the graph another person might be the most influential for their own, very subjective reasons.
Still, seeking for vertex importance in a given graph is a challenging problem, and one historically important example of such an algorithm is PageRank, which was described back in 1998 in the seminal paper "The Anatomy of a Large-Scale Hypertextual Web Search Engine" available at http://ilpubs.stanford.edu:8090/361/1/1998-8.pdf. In it, Sergey Brin and Larry Page laid the foundations of what ran their search engine Google when the company had just started out. While PageRank had a significant impact on finding relevant search results in the vast graph of web pages connected by links, the algorithm has since been replaced by other approaches within Google over the years. However, PageRank remains a prime example of how to rank web pages, or graphs in general, to gain a deeper understanding of it. GraphX provides an implementation of PageRank, which we will have a look at after describing the algorithm itself.
PageRank is an iterative algorithm for directed graphs that is initialized by setting the same value to each vertex, namely 1/N where N denotes the order of the graph, that is, the number of vertices. It then repeats the same procedure of updating vertex values, that is, their PageRank, until we choose to stop or certain convergence criteria is fulfilled. More specifically, in each iteration a vertex sends its current PageRank divided by its out-degree to all vertices it has an outbound connection to, that is, it distributes its current PageRank evenly over all outbound edges. Vertices then sum up all the values they receive to set their new PageRank. If overall PageRanks did not change much in the last iteration, stop the procedure. This is the very basic formulation of the algorithm and we will further specify the stopping criterion when discussing the GraphX implementation.
However, we also need to slightly extend the baseline algorithm by introducing a damping factor d. The damping factor was invented to prevent so called rank sinks. Imagine a strongly connected component that has only incoming edges from the rest of the graph, then by preceding prescription this component will accumulate more and more PageRank through incoming edges in each iteration, but never "release" any of it through outbound connections. This scenario is called a rank sink and to get rid of it we need to introduce more rank sources through damping. What PageRank does is simulate the idealistic idea of a completely random user following links probabilistically with likelihood given by the link target's PageRank. The idea of damping changes this by introducing a chance of probability d the user follows their current path, and with likelihood (1-d), gets bored and continues reading a completely different page.
In our rank sink example above the user would leave the strongly connected component and end up somewhere else in the graph, thereby increasing relevance, that is, PageRank, of other parts of the graph. To wrap up this explanation, the PageRank update rule with damping can be written as follows:
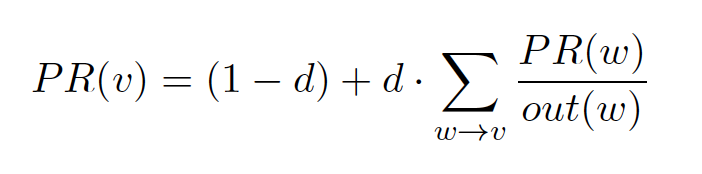
that is, to update PageRank PR for vertex v, we sum over the PageRank of all inbound vertices w divided by their respective out-degree out(w).
Spark GraphX has two implementations for PageRank, one called static, the other dynamic. In the static version, we simply carry out the preceding update rule for a fixed amount of iterations numIter specified upfront. In the dynamic version, we specify a tolerance tol for convergence, namely that a vertex drops out of the computation if its PageRank did not change at least by tol in the last iteration, which means it will neither emit new PageRanks nor update its own anymore. Let's compute PageRank in both static and dynamic versions for the tiny friendGraph. The static version with 10 iterations is called as follows:
friendGraph.staticPageRank(numIter = 10).vertices.collect.foreach(println)
After running the algorithm, we simply collect all vertices on master and print them, which yields the following:
(1,0.42988729103845036)
(2,0.3308390977362031)
(3,0.6102873825386869)
(4,0.6650182732476072)
(5,0.42988729103845036)
It's interesting to see how PageRanks change with varying numbers of iterations; see the following table for details:
| numIter / vertex | Anne | Bernie | Chris | Don | Edgar |
| 1 | 0.213 | 0.213 | 0.341 | 0.277 | 0.213 |
| 2 | 0.267 | 0.240 | 0.422 | 0.440 | 0.267 |
| 3 | 0.337 | 0.263 | 0.468 | 0.509 | 0.337 |
| 4 | 0.366 | 0.293 | 0.517 | 0.548 | 0.366 |
| 5 | 0.383 | 0.305 | 0.554 | 0.589 | 0.383 |
| 10 | 0.429 | 0.330 | 0.610 | 0.665 | 0.429 |
| 20 | 0.438 | 0.336 | 0.622 | 0.678 | 0.438 |
| 100 | 0.438 | 0.336 | 0.622 | 0.678 | 0.483 |
While the general tendency of which vertex is more important than the other, that is, the relative ranking of the vertices is already established after only two iterations, note that it takes about 20 iterations for the PageRanks to stabilize even for this tiny graph. So, if you are only interested in ranking vertices roughly or it is simply too expensive to run the dynamic version, the static algorithm can come in handy. To compute the dynamic version, we specify the tolerance tol to be 0.0001 and the so called resetProb to 0.15. The latter is nothing but 1-d, that is, the probability to leave the current path and pop up at a random vertex in the graph. In fact, 0.15 is the default value for resetProb and reflects the suggestion of the original paper:
friendGraph.pageRank(tol = 0.0001, resetProb = 0.15)
Running this yields the following PageRank values, displayed in Figure 15. The numbers should look familiar, as they are the same as from the static version with 20 or more iterations:

For a more interesting example, let's turn to the actor graph once more. With the same tolerance as in the preceding example, we can quickly find the vertex ID with the highest PageRank:
val actorPrGraph: Graph[Double, Double] = actorGraph.pageRank(0.0001)
actorPrGraph.vertices.reduce((v1, v2) => {
if (v1._2 > v2._2) v1 else v2
})
This returns ID 33024 with a PageRank of 7.82. To highlight how PageRank differs from the naive idea of simply taking in-degree as shot at vertex importance, consider the following analysis:
actorPrGraph.inDegrees.filter(v => v._1 == 33024L).collect.foreach(println)
Restricting to the vertex ID in question and checking its in-degree results in 62 incoming edges. Let's see what the top ten highest in-degrees in the graph are:
actorPrGraph.inDegrees.map(_._2).collect().sorted.takeRight(10)
This results in Array(704, 733, 746, 756, 762, 793, 819, 842, 982, 1007),which means the vertex with the highest PageRank does not even come close to having among the highest in-degrees. In fact, there is a total of 2167 vertices that have at least 62 inbound edges, as can be seen by running:
actorPrGraph.inDegrees.map(_._2).filter(_ >= 62).count
So, while this still means the vertex is in the top 2% of all vertices in terms of in-degree, we see that PageRank yields a completely different answer from other approaches.
