2
Solid in Space. Efforts and Links: Power
The motion of a body depends on the actions that its environment exerts on it. The elements developed in Volume 1 of this series have led us to the movement equations, and we now need to describe this environment, that is the forces and efforts of all types that are being exerted on the solid during its motion and condition it, in particular the instantaneous energy or power that are dispelled or exchanged. Knowing this power is a crucial step towards establishing the movement equations; but to assess it, we still need to know and describe the environment where a body is located and moving. This is the object of this current chapter.
2.1. Degrees of freedom of a solid
In a Galilean frame 
, the situation of a solid (S) is defined by six parameters; they are, for example, the three coordinates of its center of inertia G, that is the three components of the position vector 
, and the three Euler angles which express the orientation of the basis joined to the solid. And these six parameters form the maximum independent ones likely to describe the situation of a solid.
Independent means that there is no relation linking them when describing the situation of the solid. The movement equations will establish this link subsequently, once the environment has exerted its action over the way the solid moves, which they will translate in terms of relationships between these different parameters and their derivatives.
We then say that the solid is free, or that it owns 6 degrees of freedom. The number of degrees of freedom of a body in motion indicates that of its situation parameters independent from any prior relations between them.
When the number of degrees of freedom of a solid in motion is below 6, the solid is said to be linked.
2.2. Free solid
The situation of a free solid (S), to which is joined the frame 
, is observed from the Galilean frame 
. It is described by the six parameters
That of its center of inertia G is defined by the position vector
2.2.1. Velocity distributing torsor
Other than the speed 
of this point, the motion of the solid is also expressed by the rotation rate vector
and, in the particular case of an orientation defined by the Euler angles,
To the motion of (S) in 
g
is associated the velocity distributing torsor or kinematic torsor 
of reduction elements at G:
- – resultant
; - – moment at
;
with the respective partial distributing torsors
2.2.2. Kinetic torsor
The reduction elements at G of the kinetic torsor of (S) in g are defined as
2.2.3. Dynamic torsor
The reduction elements at G of the dynamic torsor 
in g are
with 
where 
2.2.4. Kinetic energy
The kinetic energy of (S) in g is given by
with 
2.2.5. Applying the fundamental principle of dynamics
Consider {Δ} the torsor for outside efforts applied to (S), depending on its situation parameters and their derivatives which are function of time. The two vector consequences deduced from the expression of the fundamental principle
are written
and are differential vector equations of form
that, after projections on appropriate axes, give us six scalar equations with six unknowns.
2.3. Linked solids and links
2.3.1. Links
The solid (S) is subject to a link in g when there exists a particular relation between its situation parameters in the frame, their first derivatives and eventually time t. The general expression of this link is
Under this form, the link is said to be nonholonomic dependent on time.
It is said to be nonholonomic independent of time when it has the following form
When the link does not depend on the first derivatives of the situation parameters, it is holonomic, dependent or independent of time, of expressions
Solid (S) is subject in g at ℓ links when its situation parameters are linked by ℓ relations of the following type
whether these links are holonomic or not, dependant or not of time.
2.3.2. Configurable links
The solid (S) is subject to g at ℓ links dependent or not on time, which restrict motion. These links are said to be configurable when its six situation parameters in the same frame depend on k independent other parameters qα, α = 1 – k and eventually on time t; we then say that the solid owns k degrees of freedom
The number of degrees of freedom k and the number of links ℓ are connected by the relation
where the number of independent parameters k can take values between 1 and 5.
The velocity distributing torsor of (S) in g then depends on k parameters qα and is expressed under the following form
2.3.3. Linked solids
In the case where the solid (S) is subject in g to ℓ configurable links independent of time that give it k degrees of freedom, we have six relations:
so
2.3.3.1. Velocity distributing torsor
The velocity distributing torsor of (S) in g is then written
hence the partial distributing torsors
2.3.3.2. Kinetic torsor
The reduction elements of the kinetic torsor of (S) in g have the following expression
2.3.3.3. Dynamic torsor
The reduction elements of the dynamic torsor of (S) in g have the following expression
These two vectors have the following form
where the different vector terms above have the following expression
2.3.3.4. Kinetic energy
The kinetic energy of (S) in g is given by
expression using the form
2.3.3.5. Applying the fundamental principle
The two vector consequences deduced from the expression of the fundamental principle
are written
and are differential vector equations of the following form
which, after projections over appropriate axes, give us six scalar equations with 6 + k unknowns. To solve this problem, it makes sense to introduce k other relations which are generally supplied by k conditions on the links.
2.4. Virtual power developed on a material set 
Consider a material set with a measure μ. To a particle M that belongs to it, we associate two vector fields:
- – one field
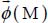by unit measure dμ(M) - – one field of virtual velocities
;
and we define the virtual power developed by the field 
under the influence of the virtual velocities field 
by the scalar
We consider that the field 
is a solidifying virtual velocities field if it satisfies the following law
Obeying this law, the vector 
behaves like the moment at M of a torsor {Ω} of which the resultant is 
and the moment at a particular point Q is 
, where 
and 
do not depend of the point M, that is
The norm of the vector 
is expressed in radians per second, like the rate of rotation, that of vector 
in meters per second since it is a velocity.
To field 
we associate the torsor {ϕ} of which the reduction elements at Q are
The virtual power developed by the field 
under the influence of the solidifying virtual velocities of moment 
is
As both vectors 
and 
do not depend on point M, the virtual power developed by the field 
under the influence of the solidifying virtual velocities field 
is given by
We therefore conclude that the virtual power developed by the field 
under the influence of the solidifying virtual velocities field 
is equal to the product of the torsors associated to these two fields, that is
2.5. Power of the efforts exerted on a solid
2.5.1. Definition
The power developed in the frame λ by a force 
acting on material element M is by definition the work per unit of time produced by this force during the displacement of M under the influence of the velocity 
, meaning the scalar product
2.5.2. Discrete force field
When considering a discrete set of forces 
acting respectively on material elements M1, M2,…, Mn, in motion under the respective effects of velocities 
, the power developed in λ by this set of forces during the displacement of the material elements Mi is defined by
2.5.3. Non-deformable mechanical set
In the case where the material elements M1, M2,…, Mn form a non-deformable mechanical set, where their distances from one another are invariable throughout their displacement, we can state the law of velocity of a non-deformable solid (S)
where OS is a reference point taken in solid (S) to which we associate the mechanical set of elements M1, M2,…, Mn.
In these conditions, we state
2.5.4. Continuous mechanical set
In the case where the particles Mi form a continuous set to which a measure μ is applied, these particles are globally subject to an elementary force field 
per unit of measure represented by the torsor {ϕ, μ} such that
the power developed in the frame λ by the field [ϕ, μ], during the displacement of continuous set upon which it is acting, is defined by
2.6. Properties of power
2.6.1. Powers developed in two distinct frames
Consider two distinct frames λ and μ and the powers that are developed within them by the force field [F] acting on solid (S) of which the motion is seen differently in each frame
This shows that the notion of power only makes sense if it refers to a well-defined frame and to the motion such as it is observed from this frame.
2.6.2. Case of a system of forces equivalent to zero acting on a solid
When the system of forces acting upon the solid (S) is equivalent to zero, the power it develops by acting on that solid during its motion in relation to λ is written
because
2.6.3. Case of a system of forces equivalent to zero acting on a deformable mechanical set
In such a case, the power developed by the system of forces is generally non-zero.
Take for example, to illustrate this case, two material elements subject to two forces in direct opposition.
with
The mechanical set being deformable, the term 
is generally non-zero if the distance M1M2 varies with time; it is, however, null if that distance is constant throughout the course of time.
2.6.4. Partial powers
The power developed by the efforts applied during the motion of a non-deformable solid, characterized by the Qi (free solid) or qα (linked solid) is given by the relation
The terms
are the partial powers developed by the efforts (known or unknown) torsor {F, S} during the motion of the solid (S). These partial powers take place primarily in the second member of the Lagrange equations in the following (see Chapter 3).