1
The World in Equations
Written in the second half of the 19th Century, the novels by French writer Jules Verne (1828–1905) recall the scientific and technological progress of his century. Verne shared the positive conception of technological progress, theorized by the French philosopher Auguste Comte (1798–1857) among others. Confident in human inventiveness, he expressed it in these terms to the French explorer Charles Lemire (1839–1912), his first biographer: “Everything I imagine will always remain below the truth, because there will come a time when the creations of science will exceed those of imagination.”
Published in 1870, Twenty Thousand Leagues Under the Sea is one of his most translated works [VER 92]. Nowadays, it is also one of the top 20 best-selling books in the world, and has given rise to numerous adaptations for cinema, television and comic strips. Professor Aronnax, a leading expert at the Paris Museum of Natural History, Conseil, his servant, and Ned Land, an experienced sailor and harpooner, board the Abraham Lincoln, in search of a sea monster. The extraordinary beast is actually a machine of steel and electricity: the Nautilus, a formidable machine designed, built and commanded by Captain Nemo in order to rule the underwater world like a master. During their long stay aboard the submersible, the three heroes of the novel will discover magnificent landscapes and experience incredible adventures. They will measure the vastness of the ocean, its resources and wealth. A dream journey for Professor Aronnax, a golden prison for Ned Land, this strange epic will take them more than twenty thousand leagues under the sea. Verne lends these words to Captain Nemo:
If danger threatens one of your vessels on the ocean, the first impression is the feeling of an abyss above and below. On the Nautilus men’s hearts never fail them. No defects to be afraid of, for the double shell is as firm as iron; no rigging to attend to; no sails for the wind to carry away; no boilers to burst; no fire to fear, for the vessel is made of iron, not of wood; no coal to run short, for electricity is the only mechanical agent; no collision to fear, for it alone swims in deep water; no tempest to brave, for when it dives below the water it reaches absolute tranquility. There, sir! That is the perfection of vessels! And if it is true that the engineer has more confidence in the vessel than the builder, and the builder than the captain himself, you understand the trust I repose in my Nautilus; for I am at once captain, builder, and engineer! [VER 92]
How to make Captain Nemo’s dream come true? How to design a ship and ensure that its crew will be able to navigate safely, in difficult sea conditions or during sensitive operations? The engineers of the 21st Century have at their disposal the experience and know-how of those who preceded them, their physical sense and the sum of their technical knowledge – as well as the feedback of tragic accidents, some of which were told, for example, in the cinema [BIG 02, CAM 97]. Other tools are also available to them: those of numerical simulation* in particular [BES 06].
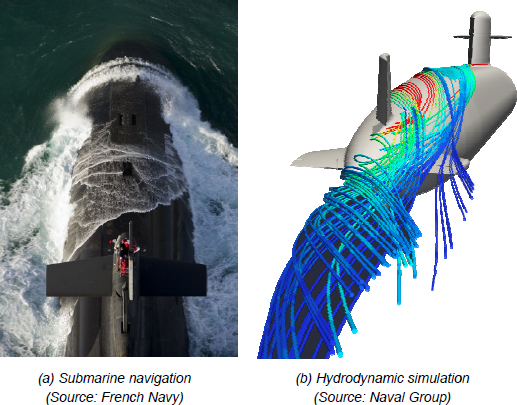
Figure 1.1. Numerical simulation nowadays accompanies the design of a ship as complex as a submarine [BOV 16, REN 15]. For a color version of this figure, see www.iste.co.uk/sigrist/simulation1.zip
1.1 Numerical modeling
1.1.1 Modeling
Numerical simulation is based on the premise that it is possible to report physical phenomena – or others (biological, economic, demographic, physiological, etc.) – using mathematical models. Consisting of a set of equations, they are constructed with a number of assumptions limiting their use. The validity of the model is attested by a confrontation with physical reality and its precision in a given field is the subject of consent in the engineering community. Under these conditions, the mathematical model acquires an important predictive capacity. It can then be used to characterize the entity under study: for example, predict the lifecycle of an electrical device, the acoustic and thermal comfort of a performance venue, the fuel consumption of a car, the efficiency of a wind turbine, or the navigation speed of a submarine.
Since the time of Jules Verne, we have lived in a world in which techniques, the fruit of knowledge and practices transmitted by women and men, are present in the smallest objects of our daily lives. Nowadays, numerical simulation accompanies the entire life cycle of many industrial projects and productions, as the following simple example shows. In order to be comfortable to wear, a pair of glasses ought to be forgotten! Lenses and frames are often fragile, and by identifying their areas of fragility, the simulation makes it possible to choose lightweight materials and resistant shapes (Figure 1.2).

Figure 1.2. Strength calculation of a pair of glasses (Source: image made with the COMSOL Multiphysics® code and provided by COMSOL, www.comsol.fr). For a color version of this figure, see www.iste.co.uk/sigrist/simulation1.zip
COMMENT ON FIGURE 1.2.– The purpose of the calculation presented here is to identify the areas of fragility of a pair of glasses. It is based on equations describing the mechanical behavior of materials (lenses, frames) and produces data that can be used by engineers. These are represented on the object using a color code: the red areas indicate potential breakpoints. The calculation is in line with our experience: in most cases, the frame will tend to break through the thin junction zone between the two lenses…
Numerical simulation is nowadays a must in the industrial world and in many scientific disciplines. It contributes significantly to innovation in this sector, by meeting two main objectives:
- – the control of technical risks. It allows the creation of regulatory dossiers, the demonstration of safety and reliability, the preparation of environmental impact studies, etc.;
- – economic performance. It contributes to the optimization of products, the demonstration of their robustness, the prediction of their performance or the reduction of their manufacturing and operating costs [COZ 09].
From their design to their dismantling, including their production, commissioning and operation, simulation becomes a general tool that benefits from the development of digital techniques. Nowadays, computer calculation makes it possible to model* many physical phenomena with satisfactory accuracy. It is improving as ECU performance accelerates. So much so that we can even imagine the possibility of conducting prototype tests before a product is put into service. The French aeronautical manufacturer Dassault Aviation, for example, has announced that it has designed one of its aircraft with the exclusive help of simulations [JAM 14]!
1.1.2 Understanding, designing, forecasting, optimizing
Simulation is thus the exploitation of the mathematical modeling of the real world as contained in the equations accounting for physical phenomena and its coupling with the computing power offered by modern computers, in order to understand, design, forecast and optimize:
- – understand? Because numerical simulation makes it possible to accurately represent many physical, chemical, biological – or social and human – phenomena (as in economics or demography). Computer calculations make it possible to provide an alternative to tests or observations carried out under real or laboratory conditions. They allow researchers to test hypotheses or theories – especially for objects of study that are sometimes inaccessible to experimentation, such as those found, for example, in the infinitely large (in astrophysics, to understand the formation of planets or black holes) or in the infinitely small (as in chemistry or biology);
- – design? Because numerical simulation is used by industry engineers to offer innovative products (e.g. integrating new materials, such as composites or those from 3D printing) or completely new products (e.g. a hydrodynamic turbine, used to recover the energy contained in underwater currents);
- – forecast? Because, to a certain extent, numerical simulation has the ability to provide data useful for analysis by technical experts. Engineers in many industrial sectors use it to demonstrate the expected performance of a construction (speed achieved by a ship in given sea conditions, resistance of a bridge or building to the effects of storms or earthquakes, fuel consumption of an engine, yield of an agricultural plot, congestion of a road network, etc.). It also makes it possible to test scenarios of interest to manufacturers – particularly in the case of accidental or exceptional events. It thus contributes to improving the safety and reliability of the various means of transport, production and products we use on a daily basis;
- – optimize? Because numerical simulation can be used to compare the different alternatives for a product that engineers help to design. It can help them in the search for optimal performance, by exploring several options at a lower cost without resorting to systematic experiments on prototypes. It thus becomes a decision-making tool and is used as such in different sectors of activity.
How is it possible to understand, design, predict and optimize through simulation? On what assumptions is a numerical simulation based? How is this technique used in industry – and in other sectors of economic or scientific activity? What are the limits of its use? How does it fit into the range of current digital technologies? It is these questions that we propose to answer in this book.
1.2 Putting the world into equations: example of mechanics
There is no numerical simulation without mathematical modeling! In the words of French mathematician Jean-Marie Souriau (1922–2012), equations are the grammar of nature [SOU 07]. Physicists, engineers or researchers have found in mathematics a simple and universal way to describe and explain some of their observations. Mathematics is thus a language developed by humans and, in its modern form, is a foundation shared by different scientific and technological communities.
The idea of putting the world into equations has crossed the history of mechanics in various forms. It also evolves according to mathematical discoveries and the conceptual means that they make available to physicists and mechanics. Let us review very briefly the main stages of this evolution.
1.2.1 Construction of classical mechanical models
In the 17th Century, the Italian physicist Galileo Galilei (1564–1642) proposed in his book The Assayer, published in 1623, a first mathematical approach to physics. His ambition was to study the movement of bodies, celestial or terrestrial, which can only be understood through abstract representations.
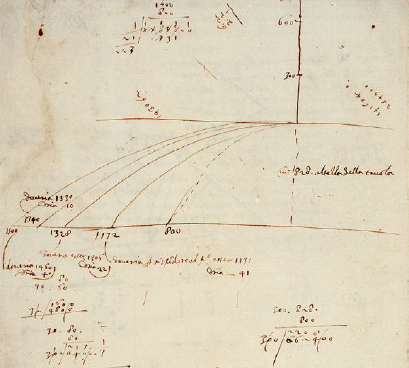
Figure 1.3. Galileo’s manuscript relating his experiences on the fall of bodies (Source: National Central Library of Florence)
COMMENT ON FIGURE 1.3.– Galileo was a complete thinker: mathematician, physicist and astronomer. Against the dogmas imposed by 16th Century religion, he supported the theory of heliocentrism, conceived by Polish mathematician and astronomer Nicolaus Copernicus (1473–1543). He made mathematics an instrument for understanding the Universe and the movement of celestial bodies. He developed experimental tools, such as the astronomical telescope, allowing him to compare his theories with observations. The approach he adopted in studying the fall of bodies is a model of a scientific method. Galileo commenced by distinguishing the forces influencing the falling movement of an object: weight, air resistance, friction on an inclined plane. He then ignored the resistance of the air and friction, to focus only on weight. He hypothesized that this movement follows a mathematical law, that is, that the speed increases in proportion to the falling time. He then drew a consequence from his hypothesis: the distance traveled is proportional to the square of time. He then developed an experiment that would confirm, or refute, his prediction. The figure reproduces folio no. 116 verso, taken from a manuscript found in Florence in 1972. In this document, Galileo noted, for example, readings of object path lengths, and various other measurements relating to his experiments on inclined planes. The latter confirm his hypotheses on the parabolic shape of the trajectories of launched objects and on the evolution of their speed. The study of the notes he left shows that his demonstration was built in a back and forth between his intuitions and their confrontation with the results of experiments – his initial hypothesis, later invalidated, was even that the speed of a falling object was proportional to the distance!
According to Galileo:
Philosophy is written in that great book which ever lies before our eyes — I mean the universe — but we cannot understand it if we do not first learn the language and grasp the symbols, in which it is written. This book is written in the mathematical language, and the symbols are triangles, circles and other geometrical figures, without whose help it is impossible to comprehend a single word of it; without which one wanders in vain through a dark labyrinth. [GAL 23]
The mathematical tools of his time were limited compared to the formal arsenal available to mechanics today. He had no equations at his disposal. Mathematical concepts were expressed through words or geometric figures. Galileo used them to formalize his observations on movement and it was the test of experimentation that then validated the modeling he proposed.
Later in the 17th Century, the English mathematician and physicist Isaac Newton (1643–1727) formulated the laws of movement in his book Philosophiae naturalis principia mathematica. Published in 1687, it is one of the first treatises on modern mechanics. We owe the translation of this text, originally written in Latin, to a woman, the French Gabrielle-Émilie le Tonnelier de Breteuil, Marquise du Châtelet (Figure 1.4). Dated 1756, a few years after the death of Émilie du Châtelet, we can still read it today.

Figure 1.4. Émilie du Châtelet (1706–1749)
COMMENT ON FIGURE 1.4.– French mathematician and physicist, Émilie du Châtelet contributed to the progress of mechanical knowledge in the 18th Century. She made Newton and Leibniz’s work known in France. She translated Newton’s book and verified some of the latter’s theoretical proposals through experience. In her translation of Newton, she thus makes theoretical corrections to the text regarding the calculation of the energy of a body, accurately establishing that it is the product of the mass and the square of the velocity [CHA 06b]. It should be noted that the equations and models encountered in simulation bear the names of the scientists – men almost exclusively – who helped to establish them. However, women have also participated, where possible, in the development of mathematics and physics. The importance of women’s contributions to science is highlighted, for example, by the French philosopher Gérard Chazal. The latter defended the following theory: “The fact of keeping (women) away (from science) is more due to ideological, social or religious reasons than to biological ones”[CHA 06b]. This theory was confirmed by recent results from researchers in cognitive sciences, showing that there are no intrinsic differences between the scientific aptitudes of men and women: “Analyses consistently revealed that boys and girls do not differ in early quantitative and mathematical ability” [KER 18]. Gérard Chazal demonstrated this with many examples, covering different disciplines and historical periods. Like Émilie du Châtelet, women are just as gifted as men for the so-called “hard” sciences (mathematics, physics or chemistry) and their past – and especially future – contribution is as decisive as that of men for the progress of knowledge and its applications for the benefit of humanity (Source: Madame du Châtelet at her desk, 18th Century, oil on canvas, Château de Breteuil).
The laws of inertia, dynamics and action/reaction are set out by Newton [NEW 56]. They form the basis of classical mechanics and many of the equations encountered in this book are an expression of this, in one form or another:
- – the first law of movement is the law of inertia: an object at rest stays at rest and an object in motion stays in motion at a constant speed and direction unless acted upon by an unbalanced force;
- – the second law of motion is that of dynamics, which Newton formulated as follows: the changes that occur in movement are proportional to the driving force; and are made in the straight line in which that force has been printed;
- – the third law of movement is that of action/reaction: action is always equal to reaction; that is, the actions of two bodies on each other are always equal and in opposite directions.
In order to solve the equations of motion, Newton laid the foundations of infinitesimal calculus, which gives meaning to the notions of derivation and integration of a mathematical function. The differential and integral calculus, discovered in the same period by the German mathematician and philosopher Gottfried Leibniz (1646–1716) in a context of rivalry between the two personalities [DUR 13], makes it possible to describe motion by means of differential equations*. These would gradually become, with partial differential equations*, the language of mechanics and remain so today. The d’Alembert equation (Box 1.1) is an example of a partial differential equation, typical of classical mechanics.

Figure 1.5. Handnotes by Gottfried Leibniz on infinitesimal calculus (Source: Gottfried Wilhelm Leibniz Bibliothek)
COMMENT ON FIGURE 1.5.– Newton and Leibniz helped to develop infinitesimal calculus. The derivative of a function describes the small variations of a quantity dependent on a variable, when the integral of a function corresponds to a continuous sum of this quantity over a given interval. The usual image illustrating these notions is that of movement: if ϕ(t) represents the speed of an object over time, the derivative dϕ/dt corresponds to the acceleration it undergoes and the integral ∫ ϕ (t)dt to the distance it travels. In order to give a mathematical existence to these notions, it is necessary to think of the ratio and the sum of quantities becoming infinitely small (they are noted dϕ and dt). How to define them, measure them? Are they calculable quantities and under what conditions? It is a question of thinking in “asymptotic” terms: the notion of “limit” is thus one of the contributions of Newton and Leibniz’s work to mathematics. It is useful for representing the dynamics of the physical world in an abstract manner.
At the turn of the 18th and 19th Centuries, the French mathematician and physicist Pierre-Simon Laplace (Figure 1.7) thought about mechanics (and the world?) in a deterministic way. Taking up the work of Galileo and Newton, he elaborated between 1799 and 1825 a Traité de Mécanique Céleste. This five-volume work is devoted to mechanics and is based on an analytical description of movement, using infinitesimal calculation.

Figure 1.7. Pierre-Simon Laplace (1749–1827)
COMMENT ON FIGURE 1.7.– Pierre-Simon Laplace was the author of many contributions in mathematics applied to astronomy, mechanics and other fields. To Napoleon I, who asked him why his treatise on cosmology did not mention God, he gave this answer: “God? Sire, I didn’t need that assumption!” (Source: Pierre-Simon Laplace by Jean-Baptiste Paulin Guérin, 1838, oil on canvas, Château de Versailles).
Laplace came to think that the universe was entirely representable by mathematics and, if we had a tool effective enough to solve the problems formulated by equations, the knowledge we would have of it would be total! He wrote as follows:
We must therefore consider the present state of the universe as the effect of its former state and as the cause of the one that will follow. An intelligence that, for a given moment, would know all the forces whose nature is animated, and the respective situation of the beings that compose it, if it were vast enough to submit these data to Analysis, would embrace in the same formula the movements of the largest bodies in the universe and those of the lightest atom: nothing would be uncertain for it and the future, as the past, would be present in its eyes (quoted by [SUS 13]).
Some mechanical systems can be described by a differential equation whose initial conditions are known, which physicists formulate as follows:
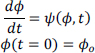
The unknown quantity, a physical quantity whose evolution is monitored, is denoted ϕ. We know its initial value, ϕ0, and its law of evolution is given by the equation describing its derivative as a known function, ψ(ϕ, t), depending on the magnitude itself and time. According to Laplace, such an equation can therefore in theory be fully calculated at any time with infinite precision!
The mathematical discoveries of the 20th Century brought strong downsides to Laplace’s assertion. By studying a solar system containing only three bodies (Earth Moon, Sun), the French mathematician Henri Poincaré (1854-1912) discovered, for example, the chaos [GLE 87] potentially hidden in classical mechanical models. He understood that it was impossible to calculate the interactions of these three bodies over a long period of time because this simplified system, although perfectly described by the equations, contained an unpredictable part.
Even in a deterministic context, the accuracy required by a calculation is not always sufficient to know what will happen, as also demonstrated by American meteorologist Edward Lorenz (1917–2008), following Poincaré. He was interested in the movement of the atmosphere, of which modeling is one of the most complex.
Describing the situation at a given moment requires knowing the temperature, pressure and speed at all points on the globe. This is a major theoretical and practical issue in mathematics and physics, some aspects of which we will study in Chapter 4 of Volume 2. In an attempt to understand some of the principles of atmospheric dynamics, Lorenz oversimplified the problem of its motion [LOR 63], as does any mathematician wishing to understand the nature of equations. He proposed a model based on a three-variable differential equation, explicitly written as:
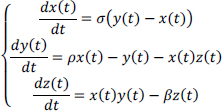
The interest of the simplification introduced by Lorenz is to describe the evolution of the atmosphere through a movement that can be graphically represented in a three-dimensional space. On the other hand, this model is so simplified that this representation does not reflect the real changes in the atmosphere!
The dynamic system proposed by Lorenz allowed him to uncover the intrinsically chaotic behavior of the system he was studying. The trajectories drawn depend on the initial conditions in an unpredictable way: thus, for two close starting points, the paths followed can suddenly move away… However, all the paths are found on longer ones in a given region of the space, designated “attractors”. The Lorenz system attractor, which he discovered in 1963, looks like a butterfly (Figure 1.8). It can be conceived as the well-known symbol of chaos theory, formulated in this question: “can the flapping of a butterfly’s wings in Brazil cause a hurricane in Europe?”
With Lorenz’s study, chance entered the scientific description of the world [LEC 16], questioning the fundamentally deterministic, and in some respects rigid, character of Newton’s and Laplace’s mechanics. The theory of chaos, developed in the middle of the 20th Century, and to which Lorenz contributed, has made part of this uncertainty a little more understandable to mathematicians and physicists [WER 09].
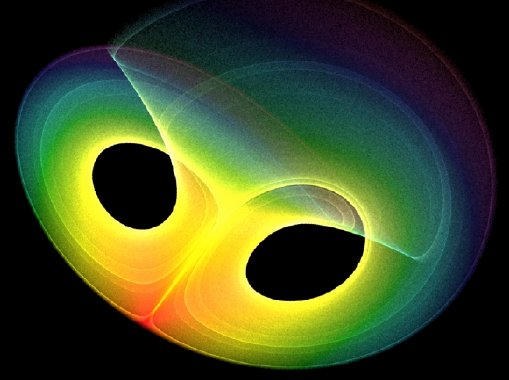
Figure 1.8. Lorenz’s attractor (Source: www.commons.wikimedia.org). For a color version of this figure, see www.iste.co.uk/sigrist/simulation1.zip
COMMENT ON FIGURE 1.8.– Lorenz studied a differential equation that allowed him to represent the atmosphere in a very simplified way. By modifying the initial conditions of this equation, he demonstrates that a low initial uncertainty results in an increasing uncertainty in the forecasts, and that this uncertainty becomes unacceptable after a long time. He concluded that this sensitivity to initial conditions makes one lose all hope of long-term forecasting. He also showed that all the trajectories corresponding to the dynamic system he was studying tended to meet in a privileged region, forming an “attractor”. It is not always possible to accurately calculate the behavior of a system composed of a very large number of interacting elements. If it is possible to determine an attractor for the system under study, one can to some extent study the system by working on the attractor instead of solving the differential equation system itself, which includes a fundamentally unpredictable part.
1.2.2 Emergence of quantum mechanics
The 20th Century also saw the emergence of the formalism of quantum mechanics, which disrupted the conception of a mechanical world governed by Newton’s laws. The greatest minds of the last century contributed to its construction (Figure 1.16): the theories they constructed made it possible to explain certain phenomena that had until then remained enigmas and to predict others… whose effective observation was accomplished decades after their prediction!
The transition from classical mechanics to quantum mechanics has been accompanied by a change of perspective on the world, the former starting from observations to build its models, the latter using its models to make predictions. In both cases, the confrontation of theory with experimentation was both a means of validating models and of imagining devices for observation and understanding.

Figure 1.16. Photograph of the participants in the 1927 Solvay conference on the theme “Electrons and photons” (Source: www.commons.wikimedia.org)
COMMENT ON FIGURE 1.16.– At the beginning of the 20th Century, the Solvay conferences brought together the greatest contributors to the advances in the physical sciences. Organized thanks to the patronage of Ernest Solvay (1838–1922), a Belgian industrialist and philanthropist, they contributed to major advances in quantum mechanics. The photograph was taken at the 1927 conference, in which Marie Curie (1867–1934), Niels Bohr (1885–1962), Paul Dirac (1902–1984), Albert Einstein (1879–1955), Werner Karl Heisenberg (1901–1976), Wolfgang Pauli (1900–1958) and Erwin Schrödinger (1887–1961) participated among others. Quantum mechanics disrupted the conceptions and understanding of the physical world then in force and pushed some of the physicists who built it to new philosophical questions. The discoveries of these scientists owe much to the exchanges and controversies that have animated their community, illustrating Schrödinger’s words: “the isolated knowledge obtained by a group of specialists in a narrow field has no value of any kind in itself; it is only valuable in the synthesis that brings it together with all the rest of knowledge and only to the extent that it really contributes, in this synthesis, to answering the question: Who are we?” [MAR 18].
Quantum mechanics aims to describe the behavior of physical systems on the scale of the infinitely small: the atoms and particles that compose them, for example. The essential is invisible to the usual eyes: the electron, this electrically charged particle that gravitates around the nucleus of an atom like the earth around the sun, has a diameter of 3×10–15 m. The equivalent of a glass bead reported at the distance between the Sun and Pluto, the planet furthest from it! On this scale, classical mechanics, which reflects the organization of our immediate world, is no longer valid. It is a special case of quantum mechanics.
A well-known physics experiment reveals the limitations of classical description. At the beginning of the 19th Century, the English physicist Thomas Young (1773–1829) understood the behavior of light by conducting an interferometry experiment, consisting of two beams interacting from the same light source.
The two sources can be obtained by means of two light-intercepting slits arranged at a short distance from each other. The interference fringes obtained have the same shape as those observed in the laboratory on the surface of a tank filled with water1: the light behaves like a wave (Figure 1.17).
The models on classical mechanics, on which the wave propagation equation and the laws of optics established by the French physicist Augustin Fresnel (1788–1827) are based, explain its behavior.

Figure 1.17. Simulation of an interferometry experiment (Source: www.commons.wikimedia.org)
COMMENT ON FIGURE 1.17.– In the figure, the light sources are located at the two points at the bottom of the image. They emit light that propagates in a cylindrical waveform. The interference pattern shows how contributions are added (light areas) or submerged (dark areas). On a screen positioned on the upper part of the image, there are alternating light and dark areas, indicating the interference.
Performing a similar experiment with particles of matter, such as electrons, we expect to observe randomly arranged impacts on a screen downstream of the sources. By taking the image of ping-pong balls bombarded on the slots, the latter pass through one or the other and touch the screen at a point. There is no reason why one region should be more privileged than another and by performing the experiment with a continuous ball flow, a series of impact points should be observed being randomly drawn on the screen. The experience gained on several occasions shows that this is not the case: the impacts gradually draw fringes similar to those obtained by wave interference (Figure 1.18).
Quantum systems have a dual nature, both wave and matter, and classical mechanics cannot explain the results of this experiment. In the world of the infinitely small, the results of experiments are often contrary to physical intuition – and overturn the models patiently built by physicists…

Figure 1.18. Fringes of electron interference observed by the team of Japanese physicist Akira Tonomura (1942–2012) in 1989 [TON 89]
COMMENT ON FIGURE 1.18.– Young’s initial experience was refined in the 20th Century so that the source emits one particle at a time. The figure shows the results of an electron interference experiment performed in 1989. Electrons are sent through Young’s slit device: in the measurement area, we observe the progressive construction of the fringes in their successive impacts – in (a) for 11 electrons, in (b) for 200, in (c) for 6,000, in (d) for 40,000 and in (e) for 140,000. Demonstrating that “each electron interacts with itself”, the experiment is in accordance with the predictions of quantum theory and illustrates the dual character of matter at this scale, both wave and particle. The models of classical mechanics, which can only explain one or the other of the behaviors, are caught in the wrong place by this interferometry experiment (source: www.commons.wikimedia.org)
For quantum mechanics, the world is a probabilistic one, as expressed in the words attributed to the Danish physicist Niels Bohr (Figure 1.19) in the foreword of this book: “Prediction is very difficult, especially about the future”2.
The state of a quantum system can be represented by a probabilistic function, which physicists are used to noting ψ. For an electron, for example, it represents the probability of the particle being in a region of space. The probability function obeys a wave equation, Schrödinger’s equation (Box 1.2): this formalism reflects the dual nature of the quantum world. By interpreting the interference experiment with the wave functions of particles interacting with themselves, quantum theory shows that the probability of impact is calculated according to a mathematical formula giving the shape of the observed fringes.

Figure 1.19. Niels Bohr (1885–1962)
COMMENT ON FIGURE 1.19.– Niels Bohr was known for his contributions to quantum mechanics [DAM 17], among other things, and set out some of its principles. Niels Bohr’s exchanges with Albert Einstein on the nature of quantum theory are a model of intellectual debate between two great scientists on the interpretation of their knowledge [BER 04]. The probabilistic nature of quantum mechanics posed a conceptual problem for Albert Einstein, which he expressed for example in the famous sentence: “God does not play dice!” The discoveries of the properties of matter made possible by Niels Bohr’s work, among others, led to the control of nuclear energy in the 1940s. The physicist quickly engaged in known uses. Bombs and power plants are two sides thereof, which it is sometimes difficult for us to accept together. Of Jewish origin, Niels Bohr fled Europe for the United States during the war in 1943. He contributed to the Manhattan project, which was the source of the American nuclear bomb launched on Japan in August 1945. After the war, he militated for the peaceful use of nuclear energy (Sources: https://www.atomicheritage.org/profile/niels-bohr, [BEL 19b]).
Conventional mechanical models can predict, with some accuracy, the results of an experiment or phenomenon, such as wind speed or wave height during a storm. Quantum models can be used to describe, for example, the state of the electron in terms of the probability of a measurement, such as its velocity or position. It also establishes that these measurements cannot be accessed at the same time with the same accuracy, although this is (theoretically) possible for the sea or wind! This impossibility is known as the principle of uncertainty, as stated by the German physicist Werner Karl Heisenberg. Quantum mechanics also relies on equations, such as those of classical mechanics [SUS 13, SUS 14]. It uses mathematical concepts and tools that have their own existence, invented by mathematicians for purposes other than explaining the mechanics of the infinitely small.
At the end of the 20th and beginning of the 21st Century, putting the world into equations continued to stimulate scientists’ thinking. American cosmologist Max Tegmark believes that the physical and mathematical worlds are inseparable. He formulated his philosophical position as follows: “the physical world is a mathematical object that we build little by little” (quoted by [DEL 99]).
The French physicist Pablo Jensen, for his part, opposes an exclusively mathematical conception of the world: “equations make it possible to combine the different forces exactly […] but we do not need a mathematical world to understand their effectiveness for physics” [JEN 18].
Further away from these theoretical questions, engineers are now developing robust methods to solve physics equations at the scale where classical mechanics is applied – but also at the quantum scale. These techniques exploit algorithms* whose current use goes beyond the sole field of scientific calculation: the 21st Century also becomes the time of algorithms [ABI 17], which change our relationship to the world beyond their technical uses [SLA 11].
1.3 Solving an equation
By simplifying the subject, engineers generally have two alternatives for solving equations: find an analytical solution – an explicit mathematical formula – or calculate a solution using a computer.
1.3.1 Finding a mathematical formula
In some situations, it is possible to find an exact solution to the equations of a physical model. This takes the form of an abstract expression that can be written using mathematical functions whose values are known. The latter are accessible in a database, in computer or paper format or using more or less elaborate calculators.
This is the case, for example, in an acoustic problem studied by Leblond et al. [LEB 09]. A pressure wave in water can be generated by an underwater explosion and is likely to damage offshore installations (an energy production station, a water pumping station, an exploration or transport vehicle). It can also be caused by the vibrations of a ship. Due to the excessive humming of its engines or fluctuations in its propeller, these can produce significant noise in the ocean and keep aquatic species away from their living areas. Detected by a military ship, they signal the presence of an enemy ship: the race for acoustic discretion of submarines is a major technical challenge that the cinema knows how to stage admirably [PET 15, POW 57, TIE 90].
Modeling the propagation of such a wave, the way it behaves when it encounters an obstacle, such as a ship’s hull, helps to protect against its effects… or to understand how dolphins communicate underwater!
The propagation equation written above in Box 1.1 provides a fairly accurate model. When it applies to a geometry of simple shape and a wave of known shape (e.g. cylindrical), it is possible to find a calculable solution – using mathematical tools, such as the Fourier transform, and known formulas, such as Bessel functions (Box 1.3).
Using a computer program, it is possible to calculate the pressure evolution using this analytical solution to the propagation equation (Figure 1.25). The validity of this calculation is established by a comparison with experimental results described in a study published 10 years earlier [AHY 98]. By simulating propagation under conditions identical to the experiment, it is then shown that the calculation accurately reproduces all the phenomena as documented by the authors of the experiment.
The calculation reproduces the physical phenomena with great precision, but remains limited to a simple shape that does not correspond to the geometric complexity of an offshore installation. However, it does provide a realistic estimate of the quantities required to understand, visualize and quantify the phenomena. The relative simplicity of the mathematical solution allows a large number of calculations to be carried out in a short time. Using a standard laptop computer, a few tens of minutes are required for a series of calculations of interest to engineers: they allow them to compare different configurations (with varying shell thicknesses or sound waves of different shape and intensity, for example). This approach is valuable for designers in the pre-dimensioning phase, when architectures are not defined in detail.

Figure 1.25. Simulation of the interaction between an acoustic wave and an immersed elastic shell [LEB 09]
COMMENT ON FIGURE 1.25.– The image shows the pressure state at a point in time of the simulation of the interaction between a shock wave and a submerged shell. We can see that the incident pressure wave (I), cylindrical in shape, touches a shell that is also cylindrical. We then observe its reflection in a wave (D) that travels in the opposite direction of the incident wave (as light is reflected on a mirror). Under the effect of the pressure it receives from the incident wave, the hull immersed in water deforms and vibrates. Two elastic waves (A0 and S0) develop in the hull, at a speed higher than the propagation speed of the acoustic wave in the water (about 4,500 m/s for the former, against 1,500 m/s for the latter). These two waves communicate their movement to the water: their signature in the fluid is visible and is thus ahead of wave I.
1.3.2 Calculating using a computer
It is in fact rather rare to find analytical solutions to the equations of mechanics and the use of a numerical technique is generally necessary. This consists in representing a curve using a set of points: engineers speak of “discretization”.
Such an operation changes from a continuous representation of the information (the curve takes values over a continuous set of points), to a discrete representation (the calculated values of the curve are calculated for a sequence of points). It is possible to construct an analogy with pointillist painting, for example that of French painter Georges Seurat (Figure 1.26). By points or by touches of color, it offers a landscape that does not need to be entirely designed to deliver its meaning. By looking at the scene, we intuitively reconstruct the missing information and guess the entire landscape. We can even imagine it beyond the limits of the painting!
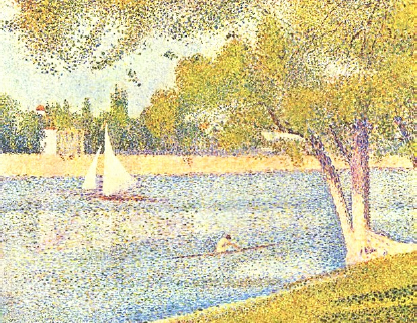
Figure 1.26. La Seine à la grande jatte, Georges Seurat (1859–1891), 1888, oil on canvas, Musées Royaux des Beaux-Arts de Belgique, Brussels. For a color version of this figure, see www.iste.co.uk/sigrist/simulation1.zip
The principle of a numerical method is to calculate an approximate solution to the equations of the physical model. Let’s take the example of an equation writing the evolution of a physical quantity as a function of position in space.
Suppose that the exact solution, noted ϕ, describes a curve represented on two axes. We are looking for an approximate solution such as a curve built from values calculated at specific locations. This collection of calculation points is noted (Xi)1≤i≤I and it contains a total of I points. In theory, the more points, the better the approximation. However, in practice, the quality of the approximation depends on many factors, which can be clarified by mathematical results.
Between two points, the evolution of the physical quantity is rendered by the section of a curve constructed with a known mathematical function. The simplest describes the shortest path between the two points. A line segment is used to calculate at any point the value of ϕ from the values of this quantity at its ends (Figure 1.27). The distance between two calculation points is noted ℎ and is also called the discretization step. It defines the resolution of the calculation and determines its accuracy.
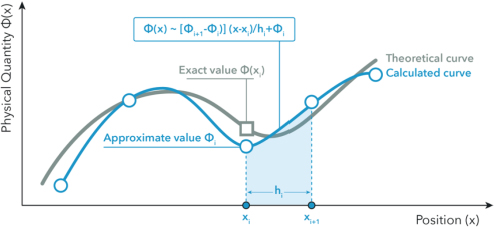
Figure 1.27. Principle of discretization (between the two points xi and xi+1, the calculated curve is a line whose formula is given in the figure). For a color version of this figure, see www.iste.co.uk/sigrist/simulation1.zip
The calculated curve thus corresponds to an approximation of the theoretical curve. We note the calculated curve ϕh the index h refers to the step and distinguishes it from the theoretical curve ϕ solution of the equations, which is not known. The approximation method used must allow the solution to be calculated accurately. It is a matter of ensuring that, when the step is smaller and smaller, the calculated function is closer to the theoretical function.
In mathematical language, it is a question of showing the convergence of the approximation process. In order to measure how ϕh approaches ϕ we use a mathematical instrument, a norm, which we note ║■║. The error made by the approximation is then measured by the norm of the difference between the theoretical and calculated solutions, in mathematical terms ║ϕ – ϕh║. The method is called “convergent” if the error becomes small when the discretization step becomes small, which is what we write:
Among the many numerical methods available, the finite element method* is nowadays the most widely used in the calculation codes used by engineers. It is indeed very well adapted to many equations and can handle a wide variety of situations encountered in mechanical engineering.
Let’s illustrate its principle for the d’Alembert equation:
Solving the equation requires finding a function that renders the expression in the left side of the equation null (which is only possible in special cases). We bypass the problem in the same way as Hercules Poirot did in Murder On the Orient Express [CHR 34]. In order to solve the case, he must consider that all those present in a closed set, the train, are guilty. In mathematical language, we formulate this idea as follows.
A function equal to zero everywhere and all the time is the solution of the equation ϕ = 0. It is also a function which, when multiplied by any function δϕ also gives a zero result, everywhere and all the time. This is expressed by the relationship ϕ•δϕ = 0 for any function δϕ. Thus, the two problems are equivalent:
where the product in brackets is here a simple multiplication:
Let’s apply the same idea to the propagation equation. We then write a problem equivalent to the meaning:
This time, the product between the brackets takes the following form:
It is a little more complex than a simple multiplication, but still calculable. It is in fact the continuous sum, over the entire calculation domain, of the product of the function searched for with any function. This expression is called the “weighted integral formulation” of the initial equation. For the propagation equation, it is written:
The transition from the propagation equation to its weighted integral formulation makes the problem somewhat more flexible. The equation is not satisfied point by point; it is satisfied on average, which better reflects the physics involved. The idea of integral formulation is basically one of the simplest and most effective – in mathematical terms, it is also one of the most elegant!
The weighted integral formulation involves the second derivative of the desired function (the equivalent of acceleration for a movement). It can be difficult or expensive to calculate accurately. To avoid this problem and for convenience, we prefer to start from another expression of the weighted integral formulation. Obtained after a calculation called “integration by parts”, it is written:

It shows a boundary term, to the right of the equal sign in the equation. It reports on physical phenomena occurring at interfaces. The roots of trees sink into the ground to find the stability necessary for them to flourish. The forces of the earth hold the tree: this is what the second member of the previous equation would express if we wanted to model a rooting.
The weighted integral formulation lends itself much better than the initial equation to a numerical approximation – and that is one of the reasons for its interest! This approximation builds the function ϕh from the values at the calculation points xi according to the relationship:
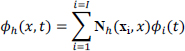
We count I calculation points: these are the nodes of a mesh made of multi-sided elements – hence the name of the method. In a three-dimensional space, the elements provide a numerical representation of the system under study. The idea of discretization may called Cartesian: in order to solve a complex problem, it would be more effective to divide it into its simple elements.
Each of the calculation points is associated with a curve – like a line for the point xi in Figure 1.27 is described by a mathematical expression. This curve is also called the approximation function and is noted Nh(xi, x). In general, we use polynomials, which allow us to describe portions of lines, parabolas, or any other complex curve3.
The variations of the approximation function (its derivatives) in space and time are calculated according to the following formulas:

If we report the calculation approximation in the weighted integral formulation, we obtain the following representation:
The unknown of this one is Φ(t) grouping the values calculated for the different points of the mesh in a data column. The number of data stored (also called “degrees of freedom”) defines the size of the problem.
The above equation is a differential and matrix equation. It concerns quantities that change over time and involves matrices: the mass matrix, noted M and the stiffness matrix, noted K. These are calculated from the functions Nh(xi, x) according to:

As the approximation functions are known, the matrices are calculated using a computer. They represent the mechanical energy of the system. The energy due to the movement of the system, or kinetic energy, is contained in the mass matrix; the energy due to the deformation of the system, or potential energy, is contained in the stiffness matrix.
Matrices are tables of numbers stored in rows and columns. The latter represent the energies of the elements resulting from the discretization of the physical system. In the mesh, an element is connected with a few neighbors and exchanges energy with them; for distant elements, there is no energy exchanged. Thus, in the table of kinetic (mass matrix) or potential (stiffness matrix) energies, there are a large number of zeros (Figure 1.28).
Folded diagonally, the upper and lower parts of the table overlap: the matrix is symmetrical. The practical consequence is that it is sufficient to store half of the numbers in the computer’s memory to perform the calculations. Efficient algorithms can significantly reduce the cost of storing matrices.

Figure 1.28. Matrix obtained with the finite element method (the black dots represent the components of the matrix different from zero: they indicate the connection between the mesh elements) [SIG 15]
Mathematicians ensure the validity of the simulation by showing that the error made during the calculation process is theoretically known. For example, they establish that the finite element method introduces two errors:
- – the first is due to discretization (the transition from a continuous to a discrete problem). The shape of the simulated part is not exactly that which is modeled and the values calculated at the mesh nodes are not exactly the exact values (Figure 1.27);
- – the second comes from the approximation (the approximate representation of the solution using given functions). In the finite element method, polynomials are most often used. The accuracy of the approximation is given by the size of the elements and the degree of polynomial functions. The smaller the size and the higher the degree, the better the accuracy. This is what a mathematical result expresses by measuring the error between the calculated solution and the exact solution:
This formula states that there are two ways to control the accuracy of the calculation: by reducing the size of the elements (h taking for example the values 0.1 then 0.01, etc.) or by increasing the degree of approximation (p taking the values 1, 2, 3, etc.). It also shows that the finite element method is convergent, an essential quality for its practical use.
The finer the discretization step, the more precise the solution… and the greater the number of calculation points. Accuracy has a cost in calculation and data storage! A compromise must then be found between the size of the numerical model (the number of unknown values) and the precision expected.
In order to determine Φ(t) at each moment from the matrix equation obtained with the finite element method, a principle similar to spatial discretization is used. It is a question of finding values at given times t1, t2…tn, tn+1 … tN–1, tN and, between two moments tn and tn+1, calculating Φ(t) from a numerical scheme involving this quantity and its successive values (Box 1.4). Step-by-step calculation methods making it possible to solve the differential equations encountered in mechanics were invented at the beginning of the 20th Century by the German mathematicians Carl David Tolmé Runge (1856–1927) and Martin Wilhelm Kutta (1867–1944). They are still widely used today by engineers for simulations from the simplest to the most complex.
Starting from the initial conditions, the dynamics of the studied system are rendered step by step. We can design this calculation process using an equivalence with chronophotographs by English photographer Eadweard James Muybridge (1830–1904), who developed shooting techniques that decompose movement and allow it to be understood (Figure 1.29).

Figure 1.29. A galloping horse and rider, Eadweard Muybridge, University of Pennsylvania, 1887 (Source: Wellcome Collection, www.wellcomecollection.org)
To be of practical interest, the numerical scheme must correctly represent the derivation operations of the quantity it makes it possible to calculate: mathematicians say that it is “consistent”. An approximation always introduces an error: when calculating the evolution of a quantity over time, this error can spread from one person to another in the calculation, until it sometimes becomes too large. The schema must limit this propagation: in this case, mathematicians describe it as “stable”. For an increasingly smaller time step, the calculated quantity approaches the theoretical quantity: this is what is expected from a so-called “convergent” scheme.
Consistency, stability and convergence are the expected properties of a calculation scheme. Without them, no accurate and reliable simulation can be envisaged. The analysis of the properties of a numerical scheme is entrusted to mathematicians. Begun in the middle of the 20th Century, it continues to be the subject of extensive research today, particularly in terms of calculation methods whose performance, such as speed of execution or robustness, is to be improved.
Beyond its application to the propagation equation, the finite element method is universal. It is adapted to the most diverse geometries and problems that can be represented with elements of various sizes and shapes. It also makes it possible to keep the same calculation structure for different problems. Whether it is a matter of ensuring the strength of a building during an earthquake, the resistance of a medical prosthesis to the weight of a patient’s walk or the quality of acoustic comfort on board an automobile, it is used by engineers in many situations, some of which we will discuss in the next chapter and several times in the second volume of this book.
- 1 In a book by the American photographer Berenice Abbott (1898–1991), the reader will also find magnificent images of physical science experiments, including interferometry [ABB 12].
- 2 The author of this quotation is not known with certainty. According to the online encyclopedia Wikipedia, these words are generally attributed to Mark Twain, Tristan Bernard… or Niels Bohr. We choose to retain the latter, giving the aphorism the probabilistic character that interests us!
- 3 On the curve shown in Figure 1.27, it can be seen that the first section looks like a piece of hyperbola and the second section approaches a line segment. It is possible to find mathematical functions describing these curves.
