5
Fractional Model-based Control of the Diffusive RC Line
5.1. Introduction
In this chapter, we intend to demonstrate that the state control of a fractional differential system (FDS) is not only a theoretical problem; on the contrary, it can be applied to control the distributed state of a diffusive system. For this purpose, this study is based on two main principles. It was demonstrated in Chapter 4 of Volume 1 that a diffusive interface can be approximated by a fractional model. Moreover, as related in Chapter 6 of Volume 1, an infinite length RC line behaves like a fractional integrator, and there is a connection between their distributed internal variables v(x,t) and z(ω,t). Hence, we intend to demonstrate that Ẕ(ω,t) state control of the fractional model of the RC line is equivalent to the control of the distributed RC line variable v(x,t).
Modeling of the diffusive interface was performed in Chapter 4 of Volume 1 using a frequency identification technique. This methodology is reserved to a theoretical analysis, making possible to justify and discriminate different models in a physical context. In practical situations, we mainly use fractional identification techniques based on time measurements [BEN 08b, MAL 08, GAB 11a, GAB 11b].
For the identification of a fractional model of the RC line, input and output data {u(t),y(t)} are generated by a numerical simulation. Consequently, these measurements are not disturbed by noise; therefore, we propose to use an elementary algorithm derived from the least-squares method for the identification of parameters {ai,bi} and of the fractional order n without using a complex nonlinear optimization algorithm as in Chapter 5 of Volume 1.
In the general case, the state control of a partial differential equation (PDE) is a complex mathematical problem that has given rise to a large number of publications [LIO 71, MOR 10]. More modestly, we are interested in the reset of the distributed variable v(x,t) of the RC line after an initial excitation. Therefore, we intend to impose
for a given value Tc, with the initial condition v(x,0) (x∈ [0,L ]), using only the interface control input. Thus, we intend to demonstrate that the reset of the RC line is equivalent imposing
with the initial condition Ẕ(ω,0), where Ẕ(ω,t) is the distributed variable of the identified fractional model.
5.2. Identification of the RC line using a fractional model
5.2.1. Introduction
The diffusive interface and its approximation by a fractional model were analyzed in Chapter 4 of Volume 1, in order to justify fractional modeling in a physical framework.
The different structures of differential models were validated by a frequency approach. However, as already mentioned, this identification approach is not suited in practice. Only a time approach based on the minimization of a quadratic criterion is really adapted for the treatment of input/output measurements, generated by a real experiment or a numerical simulation. Therefore, we intend to apply this methodology to the RC line.
5.2.2. An identification algorithm dedicated to fractional models
5.2.2.1. Principle
The general identification methodology, known as the model method or output error method [RIC 71, TRI 88], is based on the minimization of a quadratic criterion by nonlinear optimization [HIM 72] (see Chapter 5 of Volume 1).
Its fundamental interest is to be adapted to any type of model, linear or nonlinear. Its main drawback is related to its complex implementation. On the contrary, the least-squares technique [MEN 73, NOR 86] is very easy to implement but restricted to the case of a model linear in its parameters (LP model). With prior treatment of input/output data [KHA 15a], it is well suited to fractional models characterized by a known fractional order, such as commensurate order models (with n = 0.5). For non-commensurate order models, the fractional orders also have to be estimated. Several sequences of the basic algorithm with different values of the fractional order make it possible to select easily its optimal value, as in Chapter 4 of Volume 1.
5.2.2.2. One-derivative FDE model
Consider the elementary system
corresponding to the one-derivative FDE
Consider the fractional integration with order n of the two sides of equation [5.4]:
Since In{Dn(y(t))} = y(t) if the initial conditions are equal to zero, equation [5.5] is transformed into an integral equation, which can be written as
Let us define
Then, [5.7] corresponds to the linear in the parameter form (LP) required by the least-squares method
5.2.2.3. Two-derivative FDE model
Consider the non-commensurate order model
Let us define
Hn1, n2 (s) corresponds to the two-derivative FDE
As demonstrated previously, consider the fractional integration with the order m2 of the two sides of equation [5.11]:
If the initial conditions are equal to zero:
Therefore, equation [5.12] is transformed into an integral equation
Let us define
Thus, equation [5.16] corresponds to the linear in the parameter form (LP)
REMARK 1.– In practical terms, we proceed by successive integration of u(t) and y(t): the integration with the order n2 provides In2 (u(t)) and In2 (y(t)). Then, the integration with the order n1 of the previous results provides
5.2.2.4. Least-squares identification
Let us define:
- – y(t), which is a measurement (without noise);
- – ŷ(t), which is the prediction of y(t) based on the knowledge of an estimation
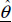using [5.8] or [5.17].
Then, with yk = y(kTe), we can express the prediction 
, where 
(regressor vector) is a function of measurements.
Consider the quadratic criterion
Then, the best estimation minimizing Jpred [EYK 74] is
It is necessary to distinguish ŷpred(t) and ŷsim(t), where ŷsim(t) represents the simulation of the system model, based only on the knowledge of the estimation and on the excitation u(t). On the contrary, ŷpred(t) is explained by the knowledge of u(t) and y(t), and of course of .
Thus
in the general case.
In order to validate an estimation 
(when does not correspond to an unstable system), it is necessary to simulate the system and compute the quadratic simulation criterion
5.2.2.5. Fractional identification with no a priori knowledge of the order
Let us consider the two cases
where the orders n or n1 are unknown.
The proposed procedure was already used in Chapter 4 of Volume 1 and applied to more complex models in [KHA 15a].
In order to determine the optimal value of the fractional order, the estimation is repeated for increasing values of 
(or 
). Therefore, we obtain the graphs 
and 
(see Figure 5.1).
Figure 5.1. Prediction and simulation quadratic criteria. For a color version of the figures in this chapter, see www.iste.co.uk/trigeassou/analysis2.zip
Of course, 
according to the distinction between ypred and ysim. The optimal value of 
is the one minimizing Jsim, i.e. 
. Of course, this procedure can be interpreted as another nonlinear optimization algorithm.
5.2.3. Simulation of the diffusive RC line
5.2.3.1. Introduction
The objective of the numerical simulation of the RC line is to provide {uk, yk} measurements required by the identification algorithm. As yk measurements (noise free) have to exactly represent the RC line, it is necessary to minimize the possible numerical simulation errors.
The dynamical behavior of the RC line obeys a diffusion equation, such as heat conduction [HOL 89]. However, simulation hypotheses for the RC line are less restrictive than those required by the simulation of heat conduction. Moreover, we can apply a negative excitation (current) to the line, whereas this excitation is not possible with heat conduction, because it would be necessary to use a heat extractor (or cooler). This remark corresponds to a necessary requirement for the control of the RC line in the last section.
Consider the line presented in Figure 5.2, which is governed by the equations (see Chapter 6 of Volume 1):
Let us recall that C and R are not resistors or capacitors but capacity and resistance densities:
Figure 5.2. The RC line
5.2.3.2. Time and space discretization
Consider Figure 5.3
Figure 5.3. Space discretization
where
i is the space index, whereas k is the time one.
with
Therefore, 
and 
are approximated by
Then, relation [5.23] becomes
Thus
Equation [5.28] represents a differential system composed of Isp +1 first-order differential equations, while [5.29] represents a difference equation system.
REMARK 2.– The heat diffusion equation, where T(x, t) is the temperature and ϕ(x, t) is the heat flux, corresponds to (see Chapter 4 of Volume 1)
Therefore, there is an equivalence between the RC line and heat diffusion
with
Thanks to this analogy, thermal resistors and thermal capacitors can be defined [HOL 89]. However, we have to be careful with this analogy.
Indeed, the heat flux through a thermal resistor creates a difference in temperatures; however, it is not accompanied by a Joule effect Ri2 as in an electrical resistor.
Similarly, a thermal capacitor stores a heat charge qT; however, this charge does not correspond to a stored energy 
as in an electrical capacitor: indeed, let us recall that the heat charge qT is itself an energy!
5.2.3.3. Boundary conditions
The RC line is a distributed system where current and voltage depend on the abscissa x and time t. Therefore, it is necessary to specify the boundary conditions, i.e. the values of i and v at x = 0 and x = L [FAR 82, HOL 89].
For an infinite length line, a condition exists at L = ∞; however, it should not be explicit (see Chapter 6 of Volume 1).
On the contrary, for a finite length line, it is necessary to specify i(L) and v(L). In the considered example, we assume that v(L) = cte and in particular v(L) = 0, which corresponds to a short circuit of the line at x = L.
This boundary condition is known as the Dirichlet condition for heat diffusion [HOL 89]. i(L,t) is not imposed; it depends on the excitation at x = 0 and the characteristics of the line.
The point x = 0 corresponds to the excitation of the line (it is also called the diffusive interface for heat diffusion). We assume that the excitation is a current generator i0(t) = i(0,t), which is equivalent to a heat flux ϕ0(t). Consequently, the voltage v(t) = v(0, t) is not imposed; it depends on i0(t) and the line.
In terms of system theory (or automatic control), i0(t) is the input and v(0, t) is the output of the RC line.
5.2.3.4. Numerical stability
The RC line is obviously a stable system. However, the stability of the difference equation system [FAR 82, HOL 89] depends on a numerical condition, linking Δt (time increment) to Δx (spatial increment).
System [5.29] is stable if
for the heat equation, which corresponds for the RC line to
As
we can also formulate this condition as
Therefore, we can conclude that for a given value RC, with L imposed, Δt max decreases if the spatial resolution is improved, i.e. if Isp is increased. Note that if Isp is increased, Δt max decreases and global computation time is increased. Hence, a compromise is necessary.
5.2.3.5. Numerical treatment of boundary conditions
Note (see Figure 5.2) that v(0,t) does not correspond to a capacitor CΔx voltage. Therefore, if we move the origin x = 0 on the first capacitor (Figure 5.4)
Figure 5.4. Interface at x = 0
we obtain
Assume that the input is a step current
with the initial condition v(0,0) = 0.
Then, we obtain
Therefore, v(t) starts with a discontinuity that does not correspond to a physical observation.
In order to solve this problem, we propose to modify the spatial discretization at x = 0 and x = L.
It is necessary to impose RΔx = 0 in [5.36] in order to suppress the discontinuity, without a modification of the global repartition of resistors RΔx and capacitors CΔx. We fulfill this requirement with the diagram of Figure 5.5.
Figure 5.5. Improved numerical interface at x = 0
We obtain
Therefore
Thus
Equation [5.41] replaces the first difference equation of system [5.29]. This modification has no impact at i = Isp since v(L, t) = 0.
5.2.3.6. Some general considerations
We intend to model the RC line at x = 0 using a fractional transfer function such as
Based on some elementary physical considerations, we can specify some characteristics of these models.
Assume a step excitation i0(t) = I0H(t) and that the line is initially at rest (i.e. v(x,0) = 0 ∀ x). Therefore, at the first instants of the transitory response, only the first cells are influenced by I0H(t), independently of line length. This means that the beginning of the graph v(0, t) is the same ∀ L. In other terms, this means that the line behaves like a fractional integrator 
.
For t → 0 (i.e. s → ∞), Hn(s) or Hn1,n2(s) behave like an integrator.
Thus
Therefore, for n = 0.5, we obtain 
.
Similarly, for n2= 0.5, we obtain
thus 
.
On the contrary, as t → ∞, all the capacitors CΔx are charged and the current I0 passes through the resistor chain.
Therefore
Thus, we can define the static gain of the two fractional models as
We can also characterize the voltage repartition inside the line for t → ∞. As v(0, ∞) = I0RL and v(L, ∞) = 0, the internal voltage v(i) = v(x) varies linearly from v(0, ∞) to 0; therefore, 
.
5.2.3.7. Experimental results
The RC line is simulated with three values of L : 50 m, 100 m and 150 m.
The simulation parameters are
Thus
Consequently, Δtmax remains the same:
and
Our choice for time discretization is Δt = 1E–03 s which ensures numerical stability.
The graphs of the three step responses are plotted in Figure 5.6; they correspond to i0(t) = I0H(t) with I0=1A.
Figure 5.6. Step responses of the RC line
Of course, the graphs are similar to those presented in Chapter 4 of Volume 1.
The internal voltage distribution for the three lengths at t = 60s is plotted in Figure 5.7.
Figure 5.7. Internal voltage distributions
For L = 50, v(0,t) reaches its asymptotic value RI0L = 5volts at t = 60s (see Figure 5.6); reciprocally, v(i,60) varies linearly from 5volts to 0 (see Figure 5.7).
The asymptotic value is not reached for L = 100 (10volts) nor for L = 150 (15volts).
In Figure 5.6, we can verify that the three graphs coincide for t > 10s, confirming that the RC line behaves like a fractional integrator:
These step responses lead to two essential conclusions:
- – in order to obtain a good estimation of the static gain
, it is necessary to include long time constant periods in the excitation u(t); - – on the contrary, if the input includes many short time periods, we obtain a good estimation of high frequency modes, i.e. of the integrator behavior.
If the identification data file uses Te = Δt (Te: sampling period) with a limited number of data points, it will favor the estimation of high frequency modes.
In order to avoid a very large number of data points, it is necessary to use undersampling, i.e. Te = NΔt. Consequently, the estimation of low frequency
modes will be favored.
5.2.4. Experimental identification
5.2.4.1. Methodology
The RC line is identified for the three previous lengths.
For each value of L , we use two data files {u,y} with Te = 10–03s and Te=5E–03s.
Figures 5.8 and 5.9 show these two data files for L = 100.
Figure 5.8. Data file:Te = 10–03s
Figure 5.9. Data file: Te = 5E–03s
Each data file is composed of two rectangular type signals, positive and negative, in order to favor the estimation of high frequency modes. These signals are followed by a relaxation period (i0(t) = 0) in order to favor the estimation of low frequency modes, obviously better with Te = 5 E–03s.
For each file, the models Hn(s) and Hn1, n2(s) are identified. The fractional orders n and n1 are estimated using the previous procedure (see section 5.2.2.5).
The graphs of Jsim and Jpred for the estimation of the fractional order with Te = 5E–03s are plotted in Figure 5.1.
5.2.4.2. Experimental results
The identification of models Hn(s) and Hn1, n2(s) is performed with the following parameters:
All the identification results for Hn(s) are presented in Table 5.1 for Te = 10–03s, and in Table 5.2 for Te = 5E–03s.
For Hn1, n2(s), the results are presented in Table 5.3 for Te = 10–03s, and in Table 5.4 for Te=5E–03 s.
We do not present the results for the commensurate order model Hn1, n2(s) (n1 = n2 = 0.5) because the corresponding models are generally unstable.
Similarly, the identification of the non-commensurate order model is not possible with Te = 10–03 s and L = 150.
Table 5.1. Identification of Hn (s) for Te =10–03s
| L | 50 | 100 | 150 |
| n | 0.65 | 0.51 | 0.5 |
| b0 | 10.57 | 1.004 | 1.003 |
| a0 | 0.139 | 0.0111 | 0.0021 |
| Jsim | 850 | 11.2 | 0.64 |
| b0/a0 | 7.6 | 90.5 | 480 |
Table 5.2. Identification of Hn (s) for Te = 5E–03s
| L | 50 | 100 | 150 |
| n | 0.86 | 0.69 | 0.57 |
| b0 | 0.890 | 0.802 | 0.913 |
| a0 | 0.171 | 0.061 | 0.028 |
| Jsim | 1450 | 4400 | 2100 |
| b0/a0 | 5.2 | 13.1 | 32.6 |
Table 5.3. Identification of Hn1, n2 (s) for Te =10–03s
| L | 50 | 100 | 150 |
| n1 | 0.83 | 0.99 | --- |
| n2 | 0.5 | 0.5 | --- |
| b0 | 0.241 | 0.0059 | --- |
| b1 | 1.093 | 1.01 | --- |
| a0 | 0.051 | 0.0011 | --- |
| a1 | 0.282 | 0.0128 | --- |
| Jsim | 4.97 | 0.71 | --- |
| b0/a0 | 4.73 | 5.36 | --- |
Table 5.4. Identification of Hn1, n2 (s) for Te = 5E–03s
| L | 50 | 100 | 150 |
| n1 | 0.84 | 0.83 | 0.94 |
| n2 | 0.5 | 0.5 | 0.5 |
| b0 | 0.385 | 0.097 | 0.0084 |
| b1 | 1.178 | 1.129 | 1.031 |
| a0 | 0.077 | 0.010 | 8.6E-04 |
| a1 | 0.477 | 0.185 | 0.027 |
| Jsim | 3.47 | 26.9 | 8.31 |
| b0/a0 | 5.0 | 9.7 | 9.8 |
5.2.4.3. Comments
The values of Jsim obviously prove that the model Hn1, n2 (s) provides a better approximation of the RC line than the model Hn(s), regardless of the value of Te. Nevertheless, the model Hn(s) is a fair approximation for Te = 10–03s.
Theoretically, this model would be inappropriate to approximate the RC line (see Chapter 4 of Volume 1). In fact, since with Te = 10–03s, the estimation of high frequency modes is favored; thus, Hn(s) represents a high frequency approximation of the fractional integrator behavior.
The value is computed for each identified model: it represents the theoretical static gain, i.e. 5 for L = 50 , 10 for L = 100 and 15 for L = 150.
For Te = 10–03s , all the values of are far from their theoretical value: this is the confirmation that the models Hn(s) and Hn1, n2 (s) provide only a good approximation of high frequency modes. On the contrary, for Te = 5E–03s, is a better approximation of the static gain, mainly for L = 50 , i.e. the two corresponding models are a fair approximation of the long time behavior. Moreover, as Jsim has a low value for Hn1, n2 (s), this means that for Te = 5 E–03s, this model performs a good compromise between the low and high frequency modes of the line, mainly for L = 50 and L = 100.
According to the remarks in section 5.2.3.6, we can verify that:
- – b0 is close to
for Hn(s) with Te = 10–03s , L = 100 and L = 150. On the contrary, b0 ≠ 1 with Te = 5 E–03s regardless of the value of L ; - – b1 is close to for Hn1, n2 (s) with Te = 10–03s , L = 50 and L = 100. This confirms that Hn1, n2 (s) gives a good compromise between the low and high frequencies, rather for the 2 low frequencies with L = 50 and L = 100, and rather for the high frequencies with L = 150.
5.3. Reset of the RC line
5.3.1. Introduction
The control of the internal state of the RC line, i.e. the control of the distribution of the v(x,t) voltage x∈ [0,L], is an ambitious objective in the general case [MOR 10]. Therefore, we limit our demonstration to the reset problem, i.e. we want to impose
verifying the distributed initial condition
The reset of the RC line can be performed by natural relaxation, i.e. by the discharge of all the capacitors in the resistive components. However, this natural relaxation is not interesting because it requires a very long time response.
Therefore, the objective is to accelerate this process and to control it using the input at x = 0 in the time interval [0, TC].
5.3.2. Natural relaxation
In order to illustrate the natural relaxation process, we perform a numerical simulation. Before performing the simulation, it is necessary to create an initial distributed state v(x, 0), which will also be the reference for further simulations.
Therefore, we apply an input i0(t) to the line (L = 100) for 0 < t < tmax. At instant tmax, we obtain the internal distribution v(x, tmax) which will be the initial condition v(x, 0).
Figure 5.10 shows the graphs of i0(t) and v(0, t) at the input of the RC line, whereas Figure 5.11 presents the distribution v(x, tmax), i.e. the initial distribution.
Figure 5.10. Initialization procedure
Figure 5.11. Natural relaxation of the RC line
With this initial condition v(x,0), we perform the natural relaxation of the RC line based on i(0,t) = 0.
Figure 5.11 shows the evolution of v(x,t) at increasing instants. We verify that at t =100s , the distribution v(x,100) is far from the objective [5.53].
Thus, these graphs demonstrate that the natural relaxation is unable to satisfy an obvious speed requirement.
5.3.3. Principle of the reset technique
The reset technique is based on two principles.
First, the RC line is modeled, at x =0 , by the two transfer functions
On the one hand, it has been demonstrated in section 5.2 that the diffusive interface can be approximated by a fractional model with a desired accuracy. However, this modeling at x = 0 does not provide (a priori) information on the distribution of v(x,t) inside the RC line.
On the other hand, the reset technique is inspired by the modeling of the infinite length RC line by a fractional integrator 
(see Chapter 6 of Volume 1).
It has been demonstrated that the real part 
of the space Fourier transform of v(x,t) verifies the same type of distributed differential equation as the internal variable z(ω,t) of the fractional integrator
and
The analogy between these differential equations suggests that
with
This analogy reveals an equivalence (for the infinite length RC line) between and z(ω,t), i.e. a connection between v(x,t) and z(ω,t). In particular, if v(x,t) = 0 ∀x, 
, implying that z(ω,t) = 0 ∀ω, which corresponds to the reset objective.
This second principle allows us to formulate the following conjecture: the control of the distributed state of the fractional integrator makes it possible to indirectly control the distributed internal state of the RC line.
Let us recall that the previous equivalence has been proved only for an infinite length line. Thus, we assume that there is also a connection between the internal state Ẕ(ω,t) of the fractional models Hn(s) and Hn1, n2 (s), and the internal distribution v(x, t) of a finite length RC line.
5.3.4. Proposed reset procedure
The reset of the RC line requires the control of the distributed state Ẕ(ω,t). Therefore, it is necessary to have the knowledge of Ẕ(ω, 0) corresponding to v(x,0)∀x∈[0,L].
For this purpose, during the initialization procedure, we apply the same input to the RC line and to its models Hn(s) or Hn1, n2 (s): therefore, this simulation provides v(x,tmax) and Hn1, n2 (s)(ω, tmax).
With Ẕ(ω, tmax), which becomes the initial distributed state Ẕ(ω,0) of the fractional model for the reset procedure, we can compute the sequence u(t) that has to be applied to the fractional integrator 
or to the double integrator 
(see Chapter 4). Finally, thanks to this sequence u(t), we can compute the excitation uFDE(t) (i.e. i0(t)) that has to be applied to the model Hn(s) (or Hn1, n2 (s)) and consequently to the RC line (see Chapter 4).
Thus, we obtain the response v(0,t) of the RC line (initialized by v(x,0) = v(x, tmax)) and the final internal distribution v(x, TC).
In order to objectively appreciate the efficiency of this methodology, the direct comparison of graphs is not sufficient.
Therefore, we have to define some more objective criteria:
- – on the distributed state Z(ω,t)
- – on the distribution v(x,TC)
- – on the control energy
Moreover, the control input is characterized by its maximum and minimum values umax/umin.
5.3.5. Experimental results
The objective is to compare the different resets performed for the three lengths L = {50,100,150} using the models Hn(s) and Hn1, n2 (s) (corresponding to Te = 10–3s and Te = 5 10–3s).
All the control sequences are computed with Δt = 10–3s and kC = 300. Therefore, Tce = kCΔt = 03s.
The fractional models are simulated with the parameters ωb = 10–3rd/s, ωh = 103rd/s and J = 30.
Moreover, the control sequences are computed with αMC = 106 (for Hn(s)) and αMC = 108 (for Hn1, n2 (s)) (see Chapter 4).
We present some experimental graphs obtained with L = 100.
For Hn(s), Figures 5.12 and 5.13 present the graphs of z(ω,t) and v(x,t) (initial and final values).
Figure 5.12. Initial and final distribution of the distributed state
Figure 5.13. Initial and final distribution of the space variable
Figure 5.14 presents the corresponding excitation uFDE(t), the system output ymod(t) and the line output v(0, t)= yline(t).
Figure 5.14. Excitation and response of the RC line
For Hn1, n2 (s), we only present in Figure 5.15 the graphs of Ẕ(ω,t)T = [z1(ω,t) z2(ω,t)] and in Figure 5.16 the input and output of the RC line
Figure 5.15. Initial and final distribution of the distributed states
Figure 5.16. Excitation and response of the RC line
These graphs demonstrate that it is necessary to use the criteria [5.60, 5.61 and 5.62] in order to objectively appreciate the efficiency of the reset on Ẕ(ω,TC) and on v(x,TC).
In Tables 5.5–5.8, we present the different criteria obtained with the models Hn(s) and Hn1, n2 (s).
Table 5.5. Hn(s) with Te =10–3s
| L | 50 | 100 | 150 |
| crit_z | 0.068 | 0.13 | 0.14 |
| crit_u | 5.6E+03 | 1.3E+04 | 1.4E+04 |
| umax/umin | 46/-62 | 60/-100 | 65/-103 |
| crit_v | 0.039 | 0.093 | 0.088 |
| L | 50 | 100 | 15 0 |
| crit_Ẕ | 1.9E-04 | 4.4E-04 | ---- |
| crit_u | 10.1E+03 | 3.6E+04 | ---- |
| umax/umin | 30/-55 | 47/-93 | ---- |
| crit_v | 3.7E-05 | 1.6E-04 | ---- |
| L | 50 | 100 | 150 |
| crit_Ẕ | 0.045 | 0.097 | 0.12 |
| crit_u | 3.1E+03 | 8.9E+03 | 1.2E+04 |
| umax/u¬ | 35/-36 | 55/-80 | 65/-95 |
| crit_v | 0.023 | 0.031 | 0.065 |
Table 5.8. Hn1, n2 (s) with Te = 5E–03s
| L | 50 | 100 | 150 |
| crit_z | 8.5E-05 | 2.6E-04 | 4.4E-04 |
| crit_u | 5.5E+03 | 1.8E+04 | 3.4E+04 |
| umax/umin | 26/-44 | 38/-70 | 47/-92 |
| crit_v | 2.6E-05 | 6.9E-05 | 1.3E-04 |
Finally, we test the influence of the control input uFDE(t) for L = 100m with Hn1, n2 (s) and Te = 5E–03s for different values of kC. The corresponding results are presented in Table 5.9.
Table 5.9. Influence of kC
| kC | 300 | 600 | 1200 |
| crit_z | 2.4E-04 | 4.5E-06 | 3.3E-08 |
| crit_u | 1800 | 480 | 11.4 |
| umax/umin | 38/-70 | 7/-11.5 | 1.35/-1 |
| crit_v | 6.9E-05 | 1.1E-06 | 2.9E-07 |
| TC (sec) | 18 | 63 | 72 |
5.3.6. Comments
For the same value of L, the best results (i.e. the lower values of crit _Ẕ and crit_v) are obtained with the Hn1, n2 (s) model.
For example, with L = 100m:
- – and Te = 10–03s, we obtain crit _v = 1.6E–04 for Hn1, n2 (s) which is significantly less than crit_v = 9.3E–02 obtained for Hn(s);
- – and Te = 5E–03s, the model Hn1, n2 (s) improves the performances since we obtain crit_v = 6.9E–05 < 1.6E–04.
On the contrary, for the same model and the same Te, it is easier to control the line with L = 50m than with L = 150m. As an example, with Hn1, n2 (s) and Te = 5E–03s, we obtain crit_v = 2.6E–05 for L = 50m against crit_v = 1.3E–04 for L = 150m.
The most spectacular conclusion concerns the influence of kC on the performances (crit_Ẕ and crit_v) and in particular on the energy of the control input, as indicated by the criteria crit_u and umax/umin.
For example, with L = 100m, Hn1, n2 (s) and Te = 5 E–03s, the amplitude of the control input is decreased from umax/umin =38/–70 with kC = 300 to umax/umin = 1.35/–1 with kC = 1200.
This means that the line can be exactly reset during TC = 72s by a control input perfectly realistic (see Figure 5.17), which is obviously more interesting in comparison with the time required by the natural relaxation.
Figure 5.17. Excitation and response of the RC line
5.3.7. Conclusion
In classical automatic control, in order to control with feedback a physical system, generally nonlinear, a controller is designed using a linear model of this system, approximated at the operating point.
This model, obtained by identification or mathematical approximation, is a transfer function H(s) (or H(z)) called the black-box model which has no physical correspondence with the original system. This mathematical model has to faithfully reproduce the system dynamics, in order to ensure the essential requirements of the closed-loop, such as the gain and phase margins, for robustness and stability objectives [LAN 89].
The RC line has been identified by a fractional model such as Hn1, n2 (s), with no mathematical correspondence with the physics of the line, characterized by a PDE. This fractional model can be used in a classical way for the design of a feedback controller if the objective is to control the dynamics of the pseudo-state variables.
In fact, this fractional model provides a more relevant information than the integer order model H(s) (or H(z)) because it makes possible to indirectly control the internal system variable v(x, t) of the RC line by the control of the distributed variable Z(ω,t) of the fractional model, as demonstrated in this chapter. This is supplementary proof of the relevance of fractional modeling.