The main difference between the neural network we built in the previous chapter and a CNN is the convolutional layer. Recall that the neural network was able to learn features related to digits. In order to be more accurate, the neural network layers need to learn more specific features. One way to do this is to add more layers; more layers would lead to more features being learned, giving rise to deep learning.

On a spring evening of 1877, people dressed in what modern-day people would consider as black-tie gathered at the Royal Institute, in London. The speaker for the evening was Francis Galton, the same Galton we met in Chapter 1, How to Solve All Machine Learning Problems. In his talk, Galton brought out a curious device, which he called a quincunx. It was a vertical wooden board with wooden pegs sticking out of it, arranged in a uniform, but interleaved manner. The front of it was covered with glass and there was an opening at the top. Tiny balls are then dropped from the top and as they hit the pegs, bounce left or right, and fall to the corresponding chutes. This continues until the balls collect at the bottom:

A curious shape begins to form. It's the shape modern statisticians have come to recognize as the binomial distribution. Most statistical textbooks end the story about here. The quincunx, now known as the Galton Board, illustrates, very clearly and firmly, the idea of the central limit theorem.

Our story, of course, doesn't end there. Recall in Chapter 1, How to Solve All Machine Learning Problems, that I mentioned that Galton was very much interested in hereditary issues. A few years earlier, Galton had published a book called Hereditary Genius. He had collected data on eminent persons in Great Britain across the preceding centuries, and much to his dismay, he found that eminent parentage tended to lead to un-eminent children. He called this a reversion to the mediocre:

And, yet, he reasoned, the mathematics doesn't show such things! He explained this by showing off a quincunx with two layers. A two-layered quincunx was a stand-in for the generational effect. The top layer would essentially be the distribution of a feature (say, height). Upon dropping to the second layer, the beads would cause the distribution to flatten out, which is not what he had observed. Instead, he surmised that there has to be another factor which causes the regression to the mean. To illustrate his idea, he installed chutes as the controlling factor, which causes a regression to the mean. A mere 40 years later, the rediscovery of Mendel's pea experiments would reveal genetics to be the factor. That is a story for another day.

What we're interested in is why the distribution would flatten out. While the standard it's physics! would suffice as an answer, there remains interesting questions that we could ask. Let's look at a simplified depiction:

Here, we evaluate the probability that the ball will drop and hit a position. The curve indicates the probability of the ball landing at position B. Now, we add a second layer:

Say, from the previous layer, the ball landed at position 2. Now, what is the probability that the ball's final resting place is at position D?

To calculate this, we need to know all the possible ways that the ball can end up at position D. Limiting our option to A to D only, here they are:

Now we can ask the question in terms of probability. The horizontal distances in the table are an encoding that allows us to ask the question probabilistically and generically. The probability of the ball travelling horizontally by one unit can be represented as P(1), the probability of the ball travelling horizontally by two units can be represented as P(2), and so on.

And to calculate the probability that the ball ends up in D after two levels is essentially summing up all the probabilities:

.

We can write it as such:

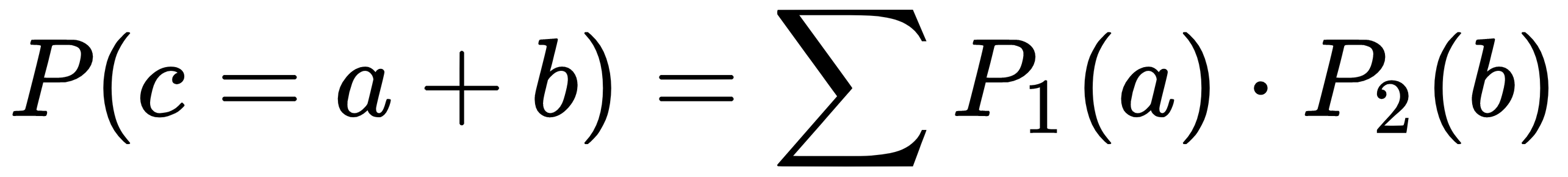
We can read it as the probability of the final distance being $c = a+b$ is the sum of $P_1(a)$, with the probability of level 1, where the ball traveled horizontally by $a$ and $P_2(b)$, with the probability of level 2, where the ball traveled horizontally by $b$.

And this is the typical definition of convolution:

If the integral scares you, we can equivalently rewrite this as a summation operation (this is only valid because we are considering discrete values; for continuous real values, integrations have to be used):

Now, if you squint very carefully, this equation looks a lot like the preceding probability equation. Instead of , we can rewrite it as :

And what are probabilities, but functions? There is, after all, a reason we write probabilities in the format $P(a)$. We can indeed genericize the probability equation to the convolution definition.

However, for now, let's strengthen our intuitions about what convolutions are. For that, we'll keep the notion that the function we're talking about has probabilities. First, we should note that the probability of the ball ending up in a particular location is dependent on where it starts. But imagine if the platform for the second platform moves horizontally:

Now the probability of the final resting place of the ball is highly dependent on where the initial starting position is, as well as where the second layer's starting position is. The ball may not even land on the bottom!

So, here's a good mental shortcut of thinking about convolutions: t's as if one function in one layer is sliding across a second function.

So, convolutions are what cause the flattening of Galton's quincunx. In essence, it is a function that slides on top of the probability function, flattening it out as it moves along the horizontal dimension. This is a one-dimensional convolution; the ball only travels along one dimension.

A two-dimensional convolution is similar to a one-dimensional convolution. Instead, there are two distances or metrics that we're considering for each layer:

But this equation is nigh impenetrable. Instead, here's a convenient series of pictures of how it works, step by step:

Convolution (Step 1):

Convolution (Step 2):

Convolution (Step 3):

Convolution (Step 4):

Convolution (Step 5):

Convolution (Step 6):

Convolution (Step 7):

Convolution (Step 8):

Convolution (Step 9):

Again, you can think of this as sliding a function that slides over another function (the input) in two dimensions. The function that slides, performs the standard linear algebra transformation of multiplication followed by addition.

You can see this in action in an image-processing example that is undoubtedly very common: Instagram.