Unit roots pose a particular problem for determining the transformation that will render a time series stationary. Time series are often modeled as stochastic processes of the following autoregressive form that we will explore in more detail as a building block for ARIMA models:

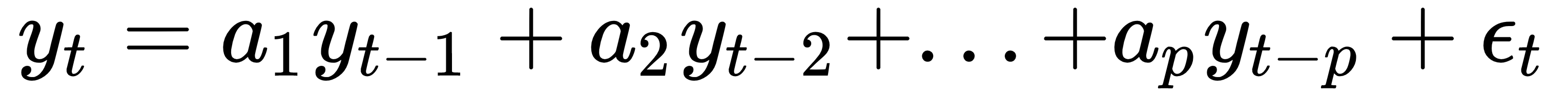
Where the current value is a weighted sum of past values plus a random disturbance. Such a process has a characteristic equation of the following form:

If one of the roots of this equation equals 1, then the process is said to have a unit root. It will be non-stationary but does not necessarily need to have a trend. If the remaining roots of the characteristic equation are less than 1 in absolute terms, the first difference of the process will be stationary, and the process is integrated (of order 1) or I(1). With additional roots larger than 1 in absolute terms, the order of integration is higher and additional differencing will be required.

In practice, time series of interest rates or asset prices are often not stationary, for example, because there does not exist a price level to which the series reverts. The most prominent example of a non-stationary series is the random walk for a time series of price, p_t, for a given starting price, p₀ (for example, a stock's IPO price) and a white-noise disturbance, ε, that satisfies the following:

Repeated substitution shows that the current value, p_t, is the sum of all prior disturbances or innovations, ε, and the initial price, p₀. If the equation includes a constant term, then the random walk is said to have drift. Hence, the random walk is an autoregressive stochastic process of the following form:

With the characteristic equation, 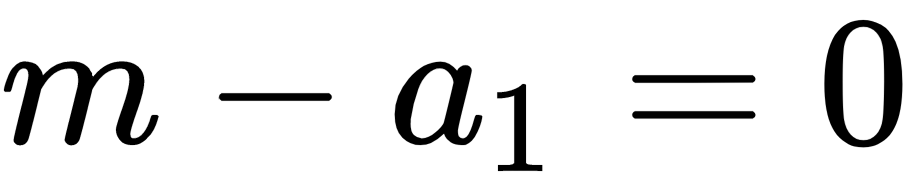, that has a unit root and is both non-stationary and integrated of order 1. On the one hand, given the i.i.d. nature of ε, the variance of the time series equals σ², which is not second-order stationary and implies that, in principle, the series could, over time, assume any variable. On the other hand, taking the first difference, Δp_t=p_t-p_t-1, leaves Δp_t=ε _t, which is stationary, given the statistical assumption about ε. 

The defining characteristic of a unit-root non-stationary series is long memory: since current values are the sum of past disturbances, large innovations persist for much longer than for a mean-reverting, stationary series.

In addition to using the difference between neighboring data points to remove a constant pattern of change, it can be used to apply seasonal differencing to remove patterns of seasonal change. This involves taking the difference of values at a lag distance that represents the length of a seasonal pattern, which is four quarters, or 12 months, apart to remove both seasonality and linear trend.

Identifying the correct transformation, and in particular, the appropriate number and lags for differencing is not always clear-cut. Some rules have been suggested, summarized as follows:

• Positive autocorrelations up to 10+ lags: Probably needs higher-order differencing.
• Lag-1 autocorrelation close to zero or negative, or generally small and patternless: No need for higher-order differencing.
• Lag-1 autocorrelation < -0.5: Series may be over-differenced. 
• Slightly over- or under-differencing can be corrected with AR or MA terms.
• Optimal differencing often produces the lowest standard deviation, but not always.
• A model without differencing assumes that the original series is stationary, including mean-reverting. It normally includes a constant term to allow for a non-zero mean.
• A model with one order of differencing assumes that the original series has a constant average trend and should include a constant term.
• A model with two orders of differencing assumes that the original series has a time-varying trend and should not include a constant.

Some authors recommend fractional differencing as a more flexible approach to rendering an integrated series stationary and may be able to keep more information or signal than simple or seasonal differences at discrete intervals (see references on GitHub).