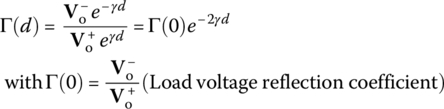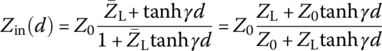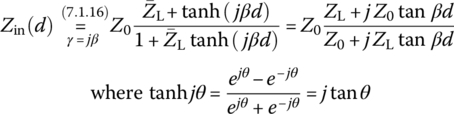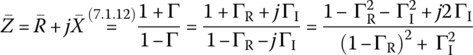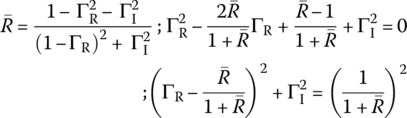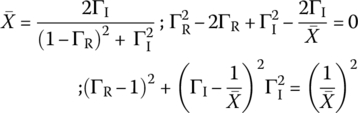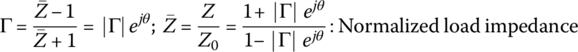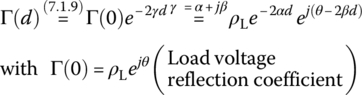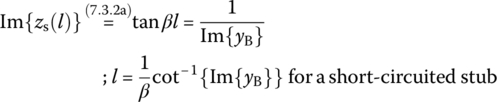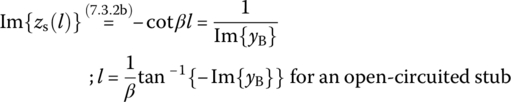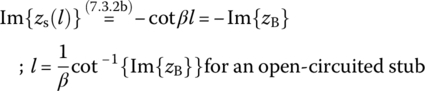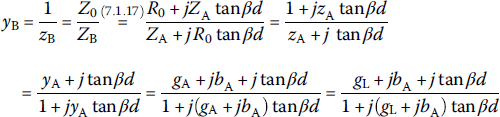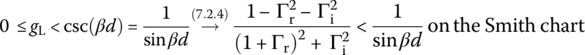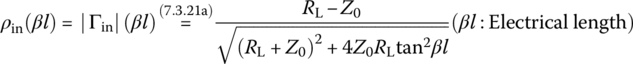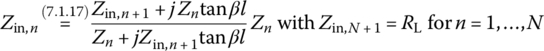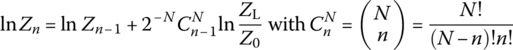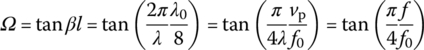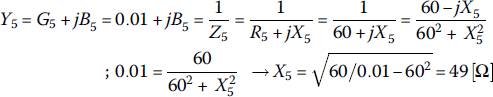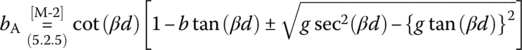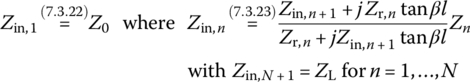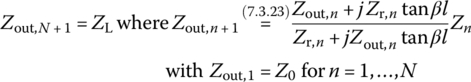7
Smith Chart and Impedance Matching
This chapter introduces the concept of the transmission line (TL) theory, impedance matching, and how the Smith Chart can be used for impedance matching.
7.1 Transmission Line
The sinusoidal steady‐state voltage and current of a TL (as depicted in Figure 7.1) at point of distance d from the load end can be written in cosine‐based phasor form as[P-1]
where ![]() and
and ![]() are called the forward(incident)/reflected voltages and currents (each propagating from the source/load to the load/source), respectively. The characteristic impedance Z0 and the propagation constant γ = α + jβ (α: attenuation constant, β: phase constant) are defined as
are called the forward(incident)/reflected voltages and currents (each propagating from the source/load to the load/source), respectively. The characteristic impedance Z0 and the propagation constant γ = α + jβ (α: attenuation constant, β: phase constant) are defined as

Figure 7.1 A transmission line (TL) terminated in a load impedance ZL.
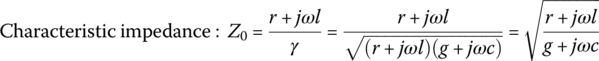
- (α: attenuation constant, β: phase constant, angular wave number, or spatial frequency)
with


Figure 7.2 The shapes of forward (incident) and reflected waves along the distance d from the load end.
If the forward (incident) and reflected voltage phasors are
the line voltage (with angular frequency ω) at point of distance d from the load can be expressed as
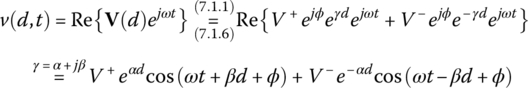
Figure 7.2(a), (b), and (c) show the shapes of forward (incident) and reflected waves when the TL is open‐ended, short‐ended, and impedance‐matched, respectively.
We divide V(d) (Eq. (7.1.1)) by I(d) (Eq. (7.1.2)) to get the input impedance Zin of the TL at point of distance d from the load as
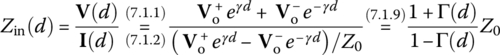
where the (input) voltage reflection coefficient Γ(d) is defined as the ratio of reflected voltage phasor to incident voltage phasor at a distance d from the load:
The voltage and current phasors at the load (d = 0) are related by the load impedance as
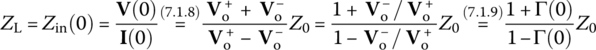
This can be solved for Γ(0) (the voltage reflection coefficient at the load, called the load [voltage] reflection coefficient) as
where the normalized load and input impedances are defined as
As a measure of the mismatch of a lossless TL with γ = jβ (β: phase constant), we define the standing wave ratio (SWR) and attenuation ratio (ATR) as
where
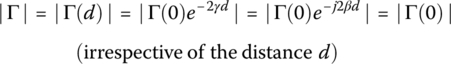
We can substitute Eq. (7.1.9) into Eq. (7.1.12) to rewrite the (normalized) load impedance as
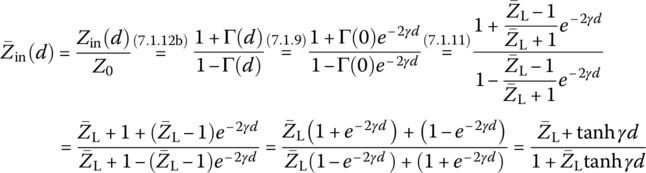
or
This can be written for a lossless TL (with an imaginary propagation constant γ = jβ = j2π/λ) terminated with a load impedance ZL as
This implies that the input impedance has the same value at every one‐half wave length (λ/2), i.e. at d ± nλ/2 (n: an integer) on a lossless TL terminated with a load impedance ZL since
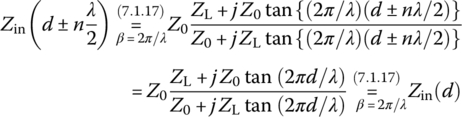
At points of distance d = nλ/2 (n: an integer), the input impedance of a lossless TL terminated with a load impedance ZL is the same as the load impedance:
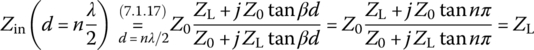
Especially, at point of distance d = λ/4, the input impedance of a lossless TL terminated in a load impedance ZL turns out to be

This can be used to determine the characteristic impedance of a λ/4‐length lossless line, called a quarter‐wave (λ/4) (impedance) transformer, with a desired input impedance Zin,d as
In addition to the SWR, as another measure of discontinuity at the load in a TL, the return loss (RL) is defined as the ratio of the incident power to (negatively) reflected power if Γ(0) is real‐valued and negative, i.e. Γ(0) < 0:

If Γ(0) is real‐valued and positive, i.e. Γ(0) > 0, the reflection loss (RFL) is defined as
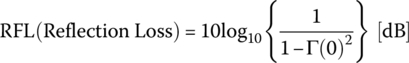
If Γ(0) = 0 (perfect impedance matching between the line and the load), we have RL = ∞ and RFL = 0. Figure 7.3 shows the lower part of Smith chart giving the SWR, RL/RFL, etc., where the values of the SWRs and RLs for Γ = −0.5 and Γ = 0.5 can be read as
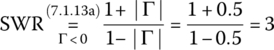
To see how the voltage reflection coefficient is related with the power flow along the TL, let us rewrite Eqs. (7.1.1) and (7.1.2) for the total voltage and current as

Figure 7.3 Lower part of Smith chart giving the Standing Wave Ratio (SWR), return/reflection loss, and reflection/transmission coefficients. (A part of the Smith chart from https://leleivre.com/rf_smith.html)
Then, the time‐average power flow along the TL at a point of distance d from the load can be written as
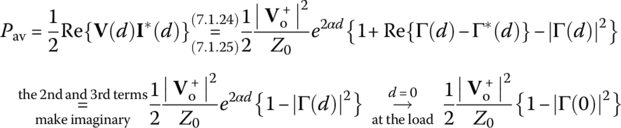
Here, |Γ(0)|2 may well be called the power reflection coefficient.
7.2 Smith Chart
The Smith chart was developed by P. W. Smith as a graphical tool to analyze and design TL circuits, in 1939. It can be used for the conversions between reflection coefficients and normalized impedances based on Eq. (7.1.12):
This can be reduced to two real equations each corresponding to the real and imaginary parts:
where
Eqs. (7.2.2a,b) represent two families of circles, each called resistance circles for ![]() = constant and reactance circles for
= constant and reactance circles for ![]() = constant, respectively, that constitute the Smith chart as plotted in Figure 7.4. Note that the center (
= constant, respectively, that constitute the Smith chart as plotted in Figure 7.4. Note that the center (![]() , 0) of resistance circle gets closer to (1,0) as
, 0) of resistance circle gets closer to (1,0) as ![]() and the center (1,
and the center (1,![]() ) of reactance circle moves up or down (depending on the sign of
) of reactance circle moves up or down (depending on the sign of ![]() ) as
) as ![]() .
.
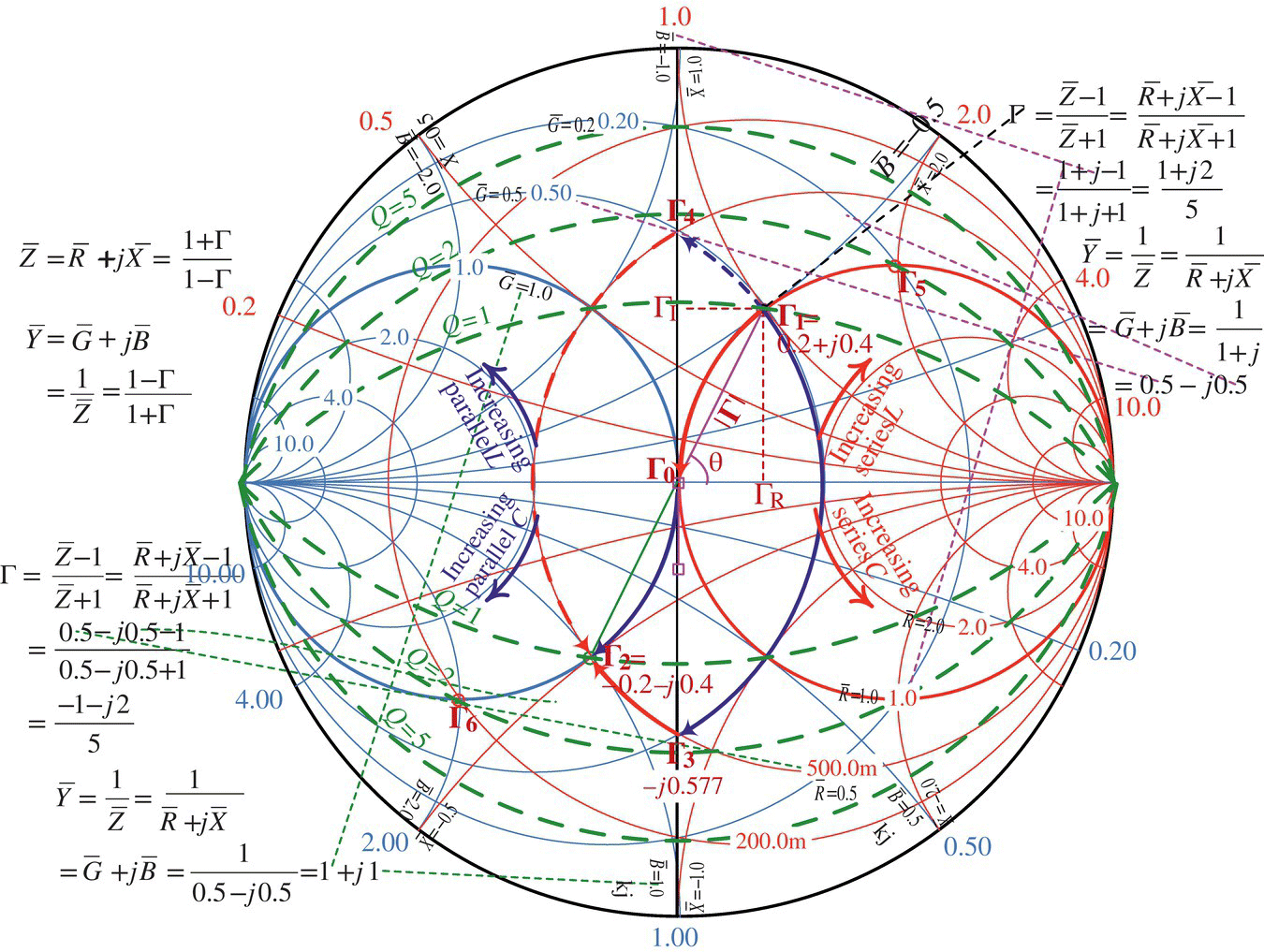
Figure 7.4 The Smith chart.
Likewise, the normalized admittance is related with the reflection coefficient as
only with the reversed sign of Γ in comparison with Eq. (7.2.1). This implies that conductance circles for ![]() = constant and susceptance circles for
= constant and susceptance circles for ![]() = constant can be obtained by making symmetric transposes of the resistance and reactance circles w.r.t. the origin (Γ = 0) or rotating them by 180° so that the sign of Γ can be reversed. In the Smith chart in Figure 7.4, conductance and susceptance circles share the point (−1,0) while the resistance and reactance circles share the point (1,0).
= constant can be obtained by making symmetric transposes of the resistance and reactance circles w.r.t. the origin (Γ = 0) or rotating them by 180° so that the sign of Γ can be reversed. In the Smith chart in Figure 7.4, conductance and susceptance circles share the point (−1,0) while the resistance and reactance circles share the point (1,0).
Note that a point on the Γ‐plane (in the Smith chart) represents the (input) voltage reflection coefficient at a distance d from the load:
Figure 7.6(b) shows several insert functions (like connecting a resistor/inductor/capacitor, an open stub, or a short(‐circuited) stub in series or parallel with the load side) that can be activated by clicking on the corresponding button in the toolbar.
7.3 Impedance Matching Using Smith Chart
7.3.1 Reactance Effect of a Lossless Line
From Eq. (7.1.17), we see that connecting a lossless TL (with an imaginary propagation constant γ = jβ = j2π/λ and characteristic impedance Z0) of length l in series with a load of impedance ZL changes the impedance as
How about a short‐circuited stub (SS) with ZL = 0 and an open‐circuited stub (OS) with ZL = ∞? Their impedances will be
like those of an inductor or a capacitor, respectively. That is why a short‐circuited or an open‐circuited stub (line) is used for impedance matching where stubs can easily be fabricated in microstrip or stripline form compared with the ‘equivalent’ lumped element. To feel how connecting a stub line of length l in series with an impedance ZL affects the impedance in terms of its reflection coefficient Γ (on the Smith chart), let us run the following MATLAB script to get Figure 7.7. It shows that as the length of the stub increases, the reflection coefficient Γ rotates clockwise around the point Γ01 corresponding to the characteristic impedance Z01 of the stub line, which is not necessarily equal to the characteristic impedance Z0 for normalization. Figure 7.7 also shows the effect of connecting a lumped element of reactance X in series with an impedance ZL = RL + jXL is to rotate the reflection coefficient Γ clockwise/counterclockwise along the RL‐circle depending on the sign of the reactance as |X| increases where Γ = 1 for X = ±∞ (see Eq. (7.2.3) with ![]() = (R + jX)/Z0 = ±j∞ where Z0 = R0 > 0).
= (R + jX)/Z0 = ±j∞ where Z0 = R0 > 0).
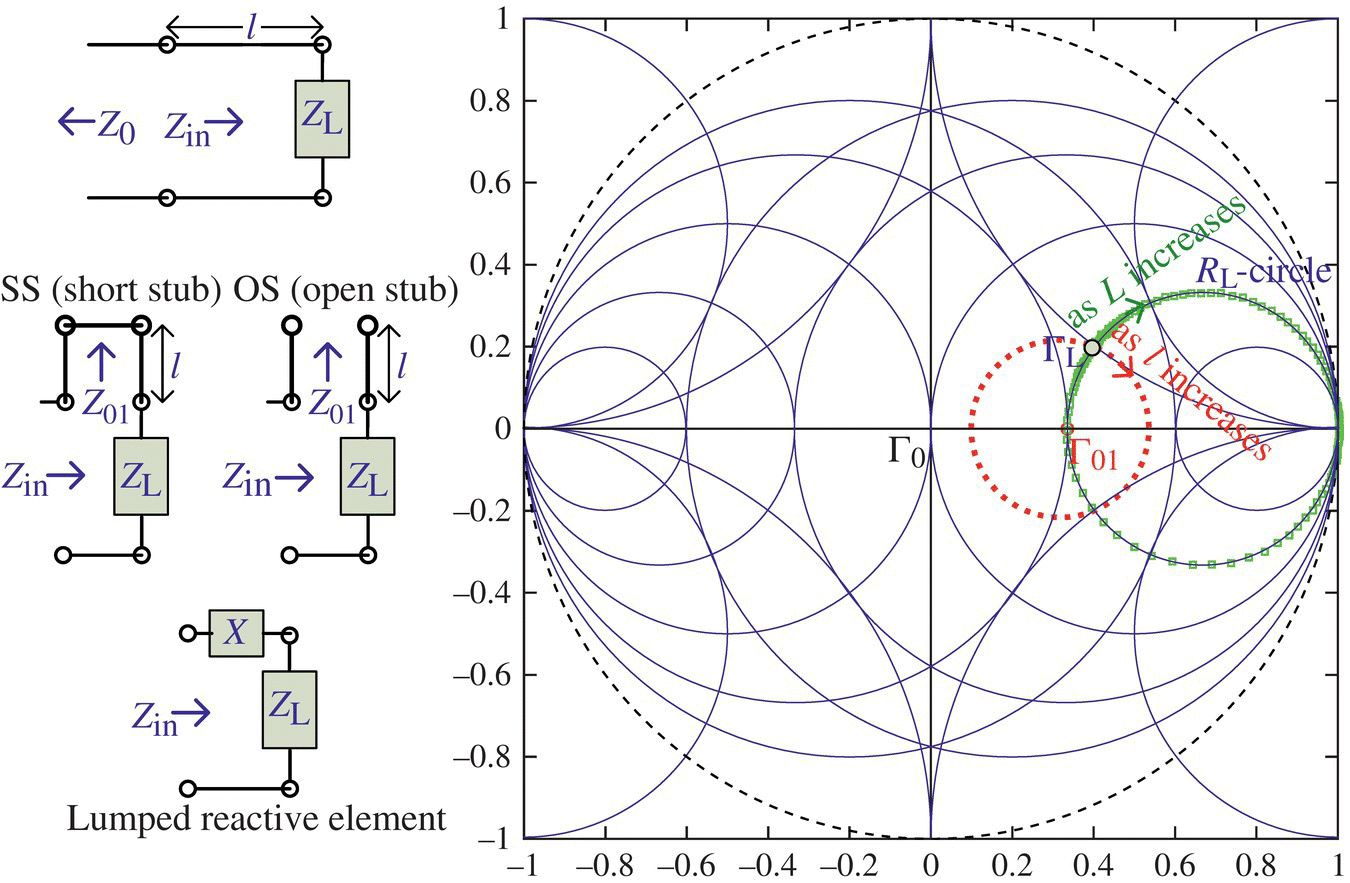
Figure 7.7 The effects of a stub and a lumped reactive element on the impedance.
7.3.2 Single‐Stub Impedance Matching
The single‐stub impedance matching (tuning) is to connect a single open‐circuited or short‐circuited lossless stub line in shunt (parallel) or series with an existing lossless TL for matching a (possibly complex‐valued) load impedance ZL to the TL of characteristic impedance R0 as shown in Figure 7.8. The problem is how distant the stub should be from the load and how long it should be.
7.3.2.1 Shunt‐Connected Single Stub
To consider how to determine the distance d from the load and the length l of the shunt stub in Figure 7.8(a), let us write the normalized impedance and admittance of the load as
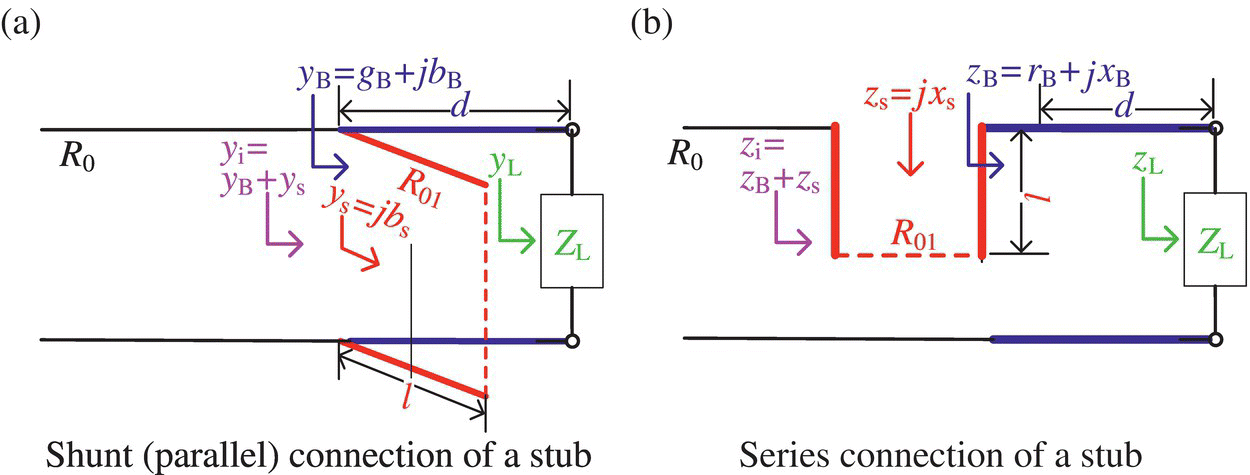
Figure 7.8 Single‐stub impedance matching.
where R0 and G0 = 1/R0 are the characteristic impedance and admittance of the TL, respectively, that are used to normalize the impedances and admittances. Noting that
- the impedance matching is achieved when the (parallel) combination of the line‐load and the shunt stub results in a unity normalized admittance/impedance corresponding to G0/R0, i.e.
- and the stub (whose admittance ys will be added to the admittance yB of the line‐load to yield the input admittance yi), short‐circuited or open‐circuited, is purely reactive/susceptive,
we should determine the distance d of the stub from the load so that the real part (conductance) of the normalized line‐load admittance can be unity:
where
If the stub has its own characteristic impedance R01 ≠ R0, yB should be multiplied with R01/R0. Now we determine the length l of the stub such that the susceptance can be bs = −Im{yB} to make the imaginary part of the input admittance yi = yB + ys zero, satisfying Eq. (7.3.4):
Note that OSs (open‐circuited stubs) are preferable for easy fabrication in microstrip or stripline form while SSs (short‐circuited stubs) are preferable for coax or waveguide.
7.3.2.2 Series‐Connected Single Stub
Similarly to the case of shunt‐connected single‐stub matching, note that
- the impedance matching is achieved when the (series) combination of the line‐load and the series stub (Figure 7.8(b)) results in a unity normalized impedance corresponding to R0, i.e.
- and the stub (whose impedance zs will be added to the impedance zB of the line‐load to yield the input impedance zi), short‐circuited or open‐circuited, is purely reactive.
We should determine the distance d of the stub from the load so that the real part (resistance) of the normalized line‐load impedance can be unity:
where
If the stub has a characteristic impedance R01 ≠ R0, zB should be multiplied with R0/R01.
Now we determine the length l of the stub such that the reactance can be xs = −Im{zB} to make the imaginary part of the input impedance zi = zB + zs zero, satisfying Eq. (7.3.8):
7.3.3 Double‐Stub Impedance Matching
The single‐stub matching introduced in the previous section requires the stub to be attached to the main line at a specific point of precise distance from the load, presenting practical difficulties because the specified point may be undesirable to attach a stub and it is very difficult to build a variable‐length coaxial line with a constant characteristic impedance. An alternative is to attach two short‐circuited stubs at fixed positions, as shown in Figure 7.11 where the distance d0 (of stub A from a load) and distance d (of stub B from stub A) can be arbitrarily chosen and fixed (say, as λ/16, λ/8, 3λ/8, etc.), and the lengths (lA and lB) of the two stubs are determined to match the load impedance ZL0 to the characteristic impedance R0 of the main lossless line. This scheme is the so‐called double‐stub matching (tuning).
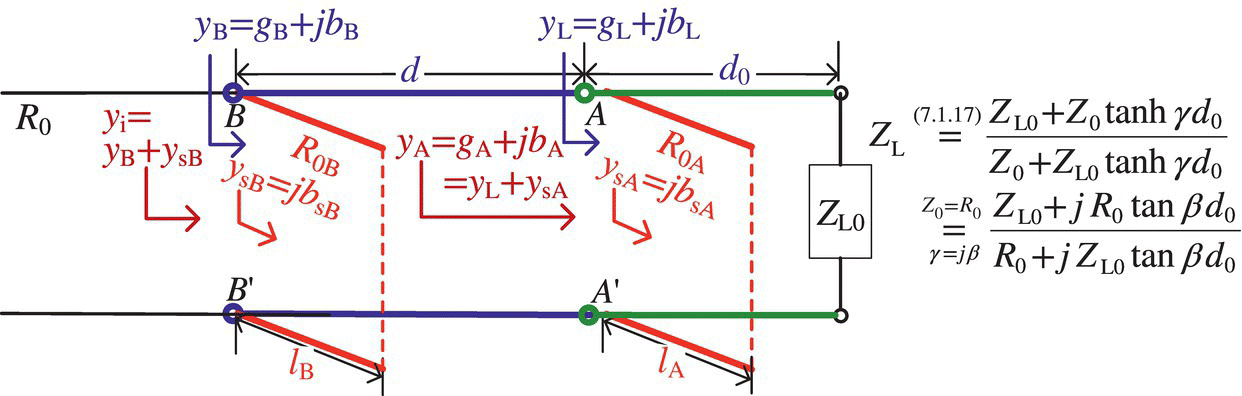
Figure 7.11 Double‐stub impedance matching.
For convenience, let the serial line of length d0 be a part of the load so that the virtual load impedance can be obtained by using Eq. (7.1.17) as
Also, let us write the normalized impedance and admittance of the load as
where the lowercase/uppercase letters stand for normalized/unnormalized values. Then, to satisfy the impedance matching condition
the real part (conductance) of yB (the input admittance at terminals B‐B' looking into the load excluding stub B) should be 1 since ysB = jbsB (the admittance of stub B) has only an imaginary part:
where
and ysB = jbsB and ysA = jbsA denote the admittances of stubs B and A, respectively, that depend on their lengths as described by Eq. (7.3.2). Thus, we should first find the value of bA such that Eq. (7.3.15) can be satisfied. Then, we can determine the susceptances {bsA, bsB} of stubs A and B as
so that the susceptance value of yB can be really bsA and that of the overall input admittance can be cancelled out to be zero. Then, the stub lengths lA and lB are determined from Eq. (7.3.7). This solution process has been cast into the above MATLAB function ‘imp_match_2stub()’.
One of the drawbacks of the double‐stub matching is that it can be used for a certain range of load impedances satisfying[M-1]
Still it is not so fatal because it is easy to make this condition satisfied by using a serial line (of a certain length d0) between the load and the first stub as long as it is allowed.
7.3.4 The Quarter‐Wave Transformer
As mentioned in Section 7.1, a real load impedance RL can be matched to a feed line of characteristic impedance Z0 by using a λ/4‐length lossless line (Figure 7.13(a)), called a QWT (quarter‐wave (λ/4) (impedance) transformer), with characteristic impedance Z1
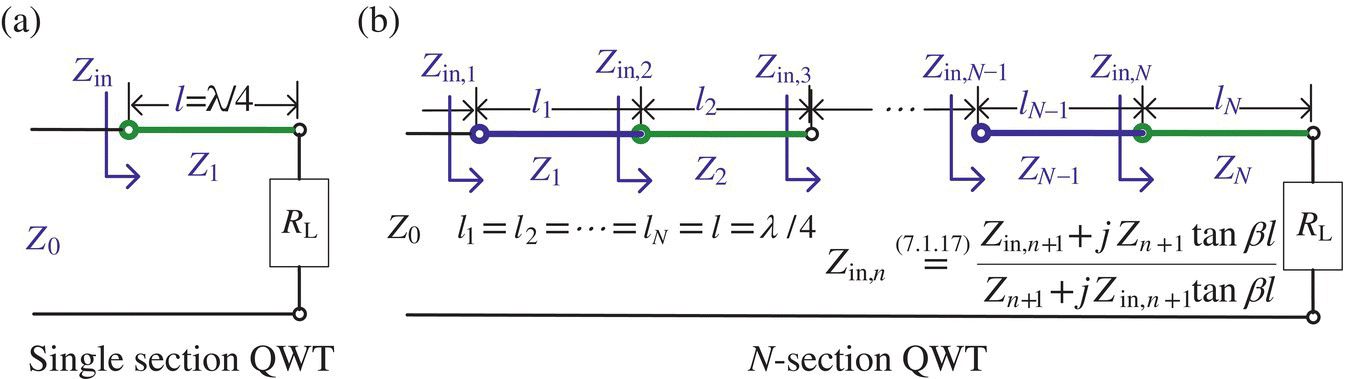
Figure 7.13 An N‐section impedance transformer.
which transforms the load impedance ZL into
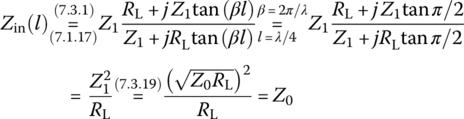
With this QWT, the reflection coefficient will be zero at β0 = 2π/λ0 (for a certain wavelength λ0) so that there is no reflected wave beyond the point distant from the load by λ0/4. However, at other frequency with βl ≠ π/2, the reflection coefficient response will be
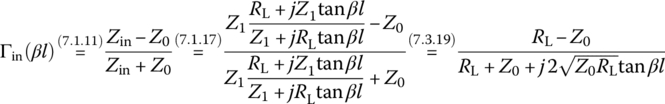
Now, we consider a multisection transformer connected between a TL of characteristic impedance Z0 and a load RL as shown in Figure 7.13 where Zn denotes the characteristic impedance of each section n. The impedance matching occurs if
where Zin,n is the input impedance of the nth section that can be obtained from Eq. (7.1.17) with the input impedance of the (n + 1)th section as the load impedance as
There are two classical N‐section transformers, the binomial transformer and the Chebyshev transformer where the reflection coefficient of the former over the frequency βd is flat while that of the latter has equiripples as a result of trying to minimize the maximum deviation for better response.
The following MATLAB function ‘multi_line()’ returns the input impedance and reflection coefficient response of a QWT with characteristic impedance vector, etc., given as input arguments.
function [Zin,Gam,bb]=multi_line(Z0s,ls,Z0,ZL,b)% To find the input reflection coefficient and impedance of a multi-line% consisting of multisections each of impedance Z0s(m) and length ls(m).% Input:% Z0s = Vector of characteristic impedances of each section of line% ls = Length(s) of each section, which is a scalar for equal length.% Z0 = Characteristic impedance of transmission line% ZL = Load resistance% b = Phase constant (a number or a vector with 2*pi*fc/c as 1st entry)% where fc=cutoff frequency, c=light velocity% Output:% Zin = Input impedance, Gam = Reflection coefficientN=numel(Z0s);if numel(ls)<2, ls=repmat(ls,1,N); endif numel(b)>1, bb=b(2:end); b=b(1); else bb=pi/90*[0:360]; endZl=@(ZL,Z0,bl)(ZL+j*Z0*tan(bl))./(Z0+j*ZL.*tan(bl))*Z0;Zi(N+1)=ZL; Zibl=ZL;for n=N:-1:1Zi(n)=Zl(Zi(n+1),Z0s(n),b*ls(n)); % Eq. (7.3.23)Z0s_(n)=sqrt(Zi(n)*Zi(n+1)); % Eq. (7.3.19)Zibl=Zl(Zibl,Z0s(n),bb*ls(n)); % Cascaded reflection responseendZin=Zi(1); Gam=(Zibl-Z0)./(Zibl+Z0); % Eq. (7.3.21b) Ref coef responseMismatching = norm(Z0s-Z0s_)
7.3.4.1 Binomial Multisection QWT
According to the design method of binomial N‐section QWT introduced in [P-1], the characteristic impedance of each section can be approximately determined in turn from the first one as
This design process has been cast into the following MATLAB function ‘binomial_QWT()’.
function Z0s=binomial_QWT(Z0,ZL,N)% To determine characteristic impedances of Nth-order binomial QWT% Input : Z0 = Characteristic impedance of the transmission line% RL = Load resistance, N = Number of sections% Output: Z0s = Characteristic impedances of each section of binomial QWTA=2^-N*(ZL-Z0)/(ZL+Z0); Zp=Z0;for n=N:-1:1logZn=log(Zp)+2^-N*nchoosek(N,N-n)*log(ZL/Z0); % Eq. (7.3.24)Zp=real(exp(logZn)); Z0s(N+1-n)=Zp;end
7.3.4.2 Chebyshev Multisection QWT
The following MATLAB function ‘Cheby_QWT()’ uses the functions ‘chebtr2()’ and ‘chebtr3()’ implementing the Collin/Riblet algorithm (presented in [O-1]) to design Chebyshev QWTs. It regards the fourth input argument as a desired value of (minimum) fractional bandwidth or a required (minimum) attenuation [dB] in the reflectionless band (relative to unmatched case) depending on whether its value is less than 1 or not.
function Z0s=Cheby_QWT(Z0,ZL,N,A_fB)% To determine the characteristic impedance of Nth-order Chebyshev QWT% Input:% Z0 = Characteristic impedance of the transmission line% RL = Load resistance% N = Number of sections% A_fb = Attenuation or Fractional bandwidth% depending on whether A_fb >=1 or not.% Output:% Z0s = Characteristic impedances of each section of Chebyshev QWT% This uses the MATLAB functions chebtr2() and chebtr3() presented in% "Electromagnetic Waves and Antennas" by Sophocles J. Orfanidis,% which is available at <<http://www.ece.rutgers.edu/~orfanidi/ewa/>,% much appreciated.if A_fB<1, Y0s=chebtr2(1/Z0,1/ZL,N,A_fb); % with A_fb=fb/f0 (fractional BW)else Y0s=chebtr3(1/Z0,1/ZL,N,A_fb); % with A_fb=As (attenuation)endZ0s=1./Y0s(2:end-1);
We can run the following MATLAB script “test_QWT.m” to use ‘binomial_QWT()’ and ‘Cheby_QWT()’ to design 1,2,3,4‐section binomial and Chebyshev QWTs and use ‘multi_line()’ to plot their reflection coefficient responses as shown in Figure 7.14, which shows the following:
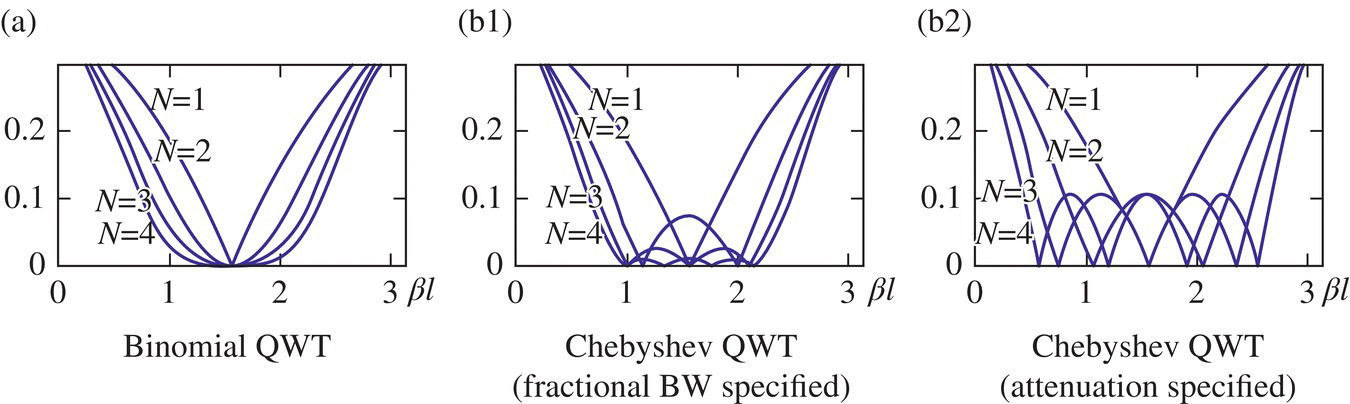
Figure 7.14 Reflection coefficient responses of binomial and Chebyshev QWTs.
- Chebyshev QWTs ((b1) and (b2)) have wider bandwidth than binomial QWTs ((a)).
- Chebyshev QWTs with the fractional bandwidth (BW) specified have smaller ripples as the number N of sections increases.
- Chebyshev QWTs with the attenuation specified have larger attenuations paying the cost of larger equiripples.
%test_QWT.mZ0=50; ZL=100; % Line characteristic impedance and Load impedancefb=0.8; % Required fractional bandwidth (f2-f1)/fc where fc=(f1+f2)/2A=10; % Attenuation[dB] of reflectionless band (relative to unmatched case)b=2*pi; l=1/4; % Phase constant and Length of each sectionfor N=1:5Z0sb=binomial_QWT(Z0,ZL,N) % Binomial QWT[Zin,Gam,bb]=multi_line(Z0sb,l,Z0,ZL,b);subplot(231), plot(bb*l,abs(Gam)), hold onZ0sCf=Cheby_QWT(Z0,ZL,N,fb) % Chebyshev QWT with fractional BW specified[Zin,Gam,bb]=multi_line(Z0sCf,l,Z0,ZL,b);subplot(232), plot(bb*l,abs(Gam)), hold onZ0sCa=Cheby_QWT(Z0,ZL,N,A) % Chebyshev QWT with attenuation specified[Zin,Gam,bb]=multi_line(Z0sCa,l,Z0,ZL,b);subplot(233), plot(bb*l,abs(Gam)), hold onend
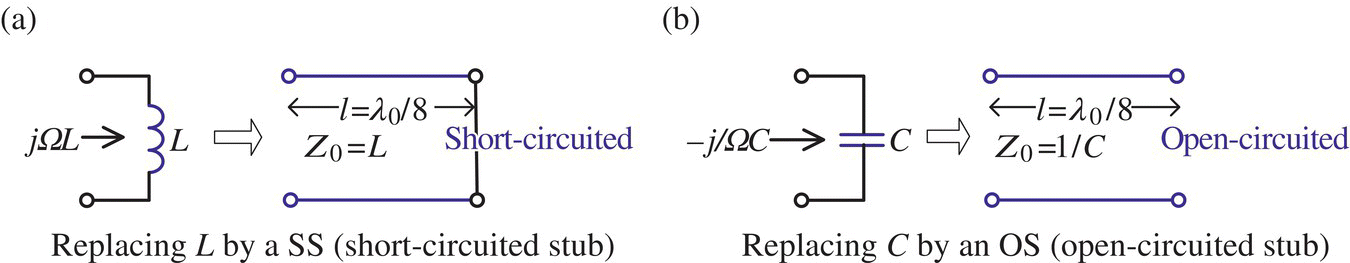
Figure 7.15 Richard's transformation.
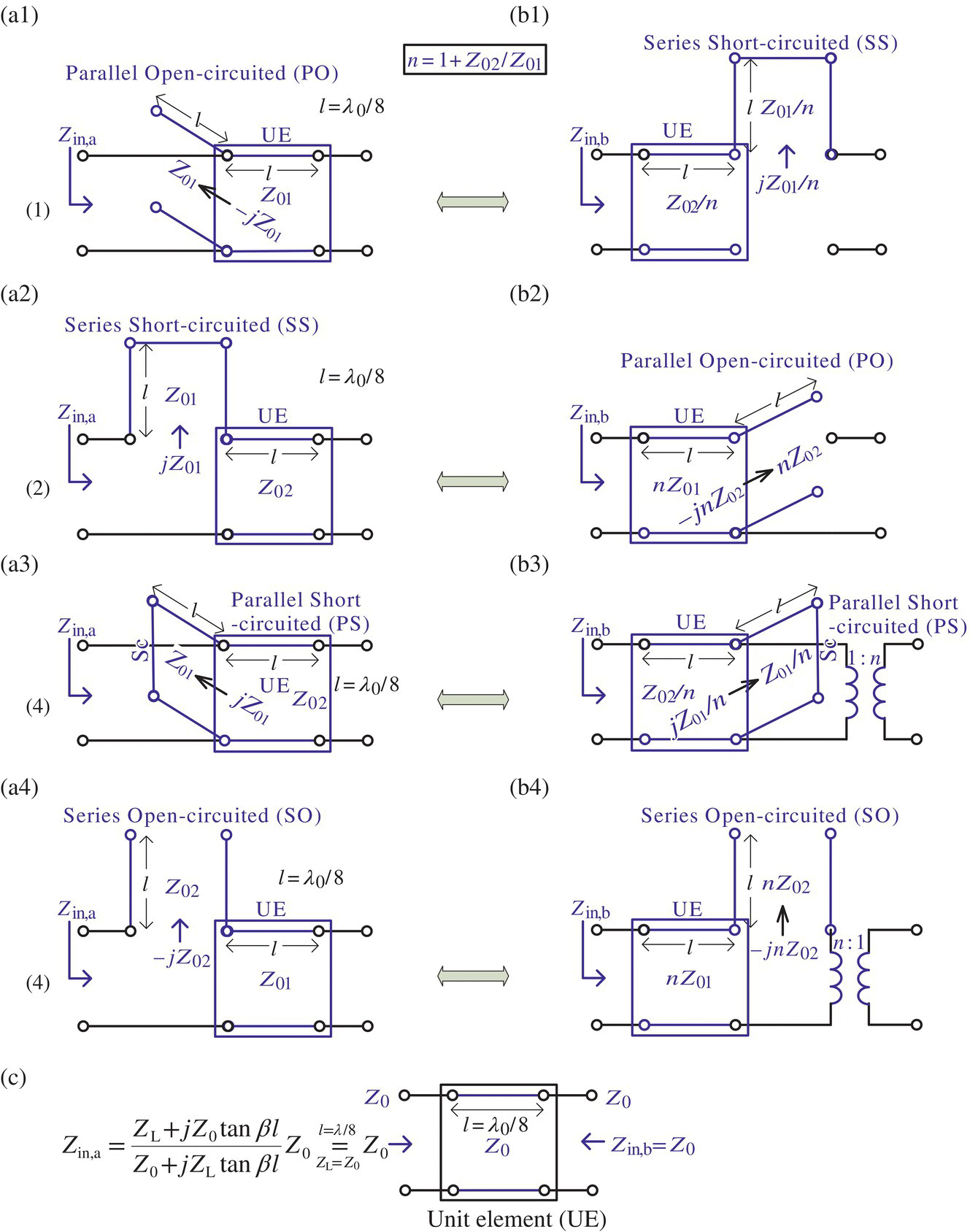
Figure 7.16 Kuroda's identities.
7.3.5 Filter Implementation Using Stubs[P-1]
The LC ladder realization using lumped elements discussed in Section 6.3.1 has two problems if they are going to be used at microwave frequencies. First, lumped elements such as inductors and capacitors are available only for a limited range of values. Second, the distances between components is not negligible at microwave frequencies. For these reasons, distributed components like short‐ or open‐circuited stubs (TL sections) are used. To implement an LC ladder using stubs, we use Richard's transformation to convert lumped elements to stubs and then use Kuroda's identities to transform series/parallel stubs into parallel/series stubs.
<Richard's Transformation>
To understand the Richard's transformation, we need to recall Eqs. (7.3.2a,b) that the impedances of short‐ and open‐circuited stubs with characteristic impedance Z0 are
and therefore, with characteristic impedance
a short‐circuited stub (SS) and an open‐circuited stub (OS) of length l = λ0/8 (λ0 = vp/f0) can act as an inductor of impedance jΩL and a capacitor of impedance 1/jΩC, that is,
respectively, at a frequency
Here vp is the phase velocity of signal propagating on the line and f0 is some reference frequency, which is often the cutoff frequency fc of a filter implemented using the SSs and OSs, corresponding to
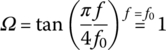
just like the unity cutoff frequency of a low‐pass filter (LPF) prototype. Since the tangent function is periodic in its argument with period π, the impedances of the SSs and OSs are periodic in f with period 4f0. Here, replacing inductance L and capacitance C by SS (with characteristic impedance Z0 = L) and OS (with characteristic impedance Z0 = 1/C), respectively, through Eq. (7.3.26) based on Eq. (7.3.28) (see Figure 7.15) is referred to as the Richard's transformation where their impedances are regarded as Eq. (7.3.27a,b).
Note that in principle, the inductors and capacitors of a lumped‐element filter can be replaced with SSs and OSs, respectively, and if all the stubs are of equal length, they are said to be commensurate.
<Kuroda's Identities>
Figure 7.16(a1)‐(b4) shows the four Kuroda's identities that can be used to transform series/parallel stubs into parallel/series stubs, physically separate stubs, and change impractical characteristic impedances into more realizable ones without changing any two‐port network property such as the input and output impedances. To understand and get familiar with them, let us show the equivalence of each pair of two‐port networks in terms of the input impedance by running the following MATLAB script “show_Kuroda.m” and checking if Zin,a = Zin,b for the four identities where the ideal transformer with turns ratio of 1: n in Figure 7.16(b3) makes the load impedance ZL (on the secondary [load] side) reflected onto the primary (source) side as ZL/n2:
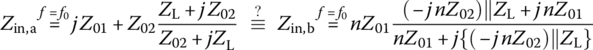
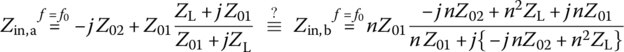
%show_Kuroda.m%Zl=@(ZL,Z0,bl)(ZL+j*Z0*tan(bl))./(Z0+j*ZL.*tan(bl))*Z0;Zu=@(ZL,Z0)(ZL+j*Z0)./(Z0+j*ZL)*Z0; % with bl=pi/4syms Z1 Z2 ZL; n=1+Z2/Z1; %% Kuroda Identity 1 (Table 8.7 of [P-1])Zina=parallel_comb([-j*Z2 Zu(ZL,Z1)]) % Fig. 7.16(a1)Zinb=Zu(j*Z1/n+ZL,Z2/n), simplify(Zina-Zinb) % Fig. 7.16(b1)% Kuroda Identity 2 (Table 8.7 of [P-1])Zina=j*Z1+Zu(ZL,Z2) % Fig. 7.16(a2)Zinb=Zu(parallel_comb([-j*n*Z2 ZL]),n*Z1) % Fig. 7.16(b2)simplify(Zina-Zinb)% Kuroda Identity 3 (Table 8.7 of [P-1])Zina=parallel_comb([j*Z1 Zu(ZL,Z2)]) % Fig. 7.16(a3)Zinb=Zu(parallel_comb([j*Z1/n ZL/n^2]),Z2/n) % Fig. 7.16(b3)simplify(Zina-Zinb)% Kuroda Identity 4 (Table 8.7 of [P-1])Zina=-j*Z2+Zu(ZL,Z1) % Fig. 7.16(a4)Zinb=Zu(-j*n*Z2+n^2*ZL,n*Z1), simplify(Zina-Zinb) % Fig. 7.16(b4)
function [Z0,Z2,SPso]=Kuroda(Z1,SPso,Z0)% SPso='Ss' for Series-to-Parallel of Z1(L) or Z1(short)% SPso='So' for Series-to-Parallel of Z1(C) or Z1(open)% SPso='Ps' for Parallel-to-Series of Z1(L) or Z1(short)% SPso='Po' for Parallel-to-Series of Z1(C) or Z1(open)% where Z0 is the characteristic impedance of a UE (unit element)% Input: Z1 = Impedance (Reactance) of the other element than UE% Z0 = Characteristic impedance of UE% Output: Z0 = Characteristic impedance of UE% Z2 = Impedance (Reactance) of the other element than UEif nargin<3|~isnumeric(Z0)|Z0==0, Z0=1; endif nargin<2, SPsp='Ss'; endSPso=upper(SPso);if SPso(1)=='S' % Series-to-Parallel conversionif SPso(2)=='S', SPso='Po'; n=1+Z0/Z1; Z2=-n*Z0; Z0=n*Z1; % Kuroda 2else SPso='Po'; Z1=abs(Z1); n=1+Z1/Z0; Z0=n*Z0; Z2=[-n*Z1 n]; % K-4end% The +/- sign of Z2 means L(short stub)/C(open stub), respectively.else % Parallel-to-Series conversionif SPso(2)=='S', SPso='Ss'; n=1+Z0/Z1; Z0=Z0/n; Z2=[Z1/n 1/n]; % K-3else SPso='Ss'; Z1=abs(Z1); n=1+Z1/Z0; Z2=Z0/n; Z0=Z1/n; % K-1endend
Figure 7.16(c) shows a unit element (UE) of characteristic impedance Z0 and length l = λ0/8 (λ0 = vp/f0) or equivalently, electrical (phase) length βl = π/4 that has input impedances at ports a and b as
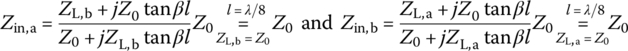
This implies that the frequency characteristic of a TL is not affected at frequency f0 = vp/λ0 by the (cascade) insertion of UE (a λ0/8‐long TL) if only its characteristic impedance is equal to that of the TL. That is why UEs are inserted between a TL and a distributed or lumped element as a preparation for applying some Kuroda's identity.
Example 7.5 Design of LPF Using Stubs [P-1]
With source/load impedances Rs = 50 Ω/ZL = 50 Ω, design a third‐order Chebyshev (equiripple) LPF with passband ripple Rp = 3 dB and fc = 4 GHz for fabrication using microstrip lines with shunt stubs only.
To design such an LPF, let us take the following steps:
- (Step 1) Determine the normalized LPF prototype element values by running the following MATLAB statements:
>>Rs=50; % Source (line) characteristic impedanceN=3; type='C'; Rp=3; % for 3rd order Chebyshev with Rp=3dBgg=LPF_ladder_coef(N,type,Rp)- This yields
gg = 3.3489e+00 7.1167e-01 3.3489e+00 1.0000e+00
- This yields
- (Step 2) Determine the normalized LC values of the prototype LPF by running the following MATLAB statements:
>>Rs0=1; pT='T'; wc=1; % for a T-type prototype filter[LCRs,LCRs_,Gs]=LC_ladder(Rs0,gg,pT,wc);LCRs, LCRs_, pretty(simplify(Gs))- This yields
LCRs = 3.3489 0.7117 3.3489 1.0000LCRs_ = 'L(h)' 'C(v)' 'L(h)' 'R(v)'5708990770823839524233143877797980545530986496/3(45566839819273848699938746290718052889107427673 s2+ 27212766570123614952226532668306611436833996800 s+ 42300936562233083587497427629177459394738126848 s+ 11417981541647679048466287755595961091061972992) - This, with ‘h’ = horizontal and ‘v’ = vertical, means the filter of Figure 7.17.1.
- This yields
- (Step 3) Convert the L/C values into the impedances of short‐/open‐circuited stubs by running
>>[Zs,SPsos]=LC2Z(LCRs,LCRs_)- where the following MATLAB function ‘
LC2Z()’ is supposed to be saved on the computer.
- where the following MATLAB function ‘
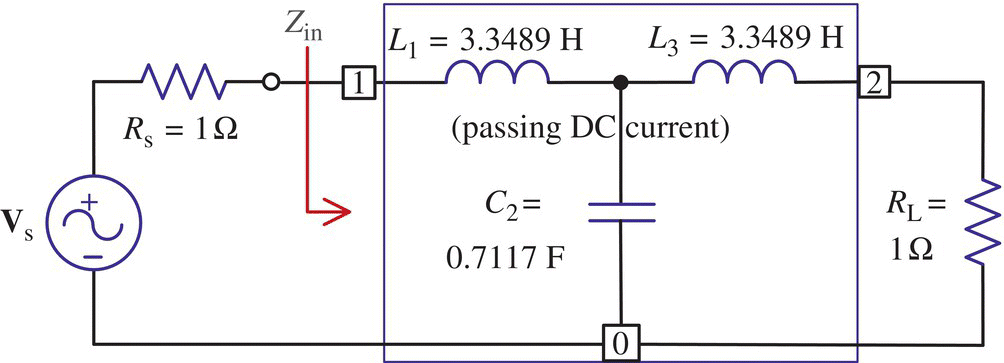
Figure 7.17.1 Normalized prototype low‐pass filter (LPF) of order N = 3.
function [Zs,SPsos]=LC2Z(LCs,LCs_)% To convert the L/C's into short/open-circuited stubsfor m=1:numel(LCs)if LCs_{m}(1)=='L'Zs(m)=LCs(m); % Eq. (7.3.26a)if LCs_{m}(3)=='h', SPsos{m}='Ss'; else SPsos{m}='Ps'; endelseif LCs_{m}(1)=='C'Zs(m)=-1/LCs(m); % Eq. (7.3.26b)if LCs_{m}(3)=='h', SPsos{m}='So'; else SPsos{m}='Po'; endelse break;endend
- This yields the characteristic impedances of the Ss (series short‐circuited stub), Po (parallel open‐circuited stub), and Ss constituting the microstrip filter in Figure 7.17.2(a):
Zs = 3.3489 -1.4052 3.3489, SPsos = 'Ss' 'Po' 'Ss' - where the +/− signs stand for L/C or short/open‐circuited stubs, respectively.
- (Step 4) Now, to use Kuroda identity 2 to convert the two SSs (series short‐circuited stubs) Z1 and Z3 into POs (parallel open‐circuited stubs), we insert UEs between Z1/Z2 and the TL (as depicted in Figure 7.17.2(b)) and run the following statements:
>>[Z0s(1),Zs(1),SPsos{1}]=Kuroda(Zs(1),SPsos{1});[Z0s(3),Zs(3),SPsos{3}]=Kuroda(Zs(3),SPsos{3});Z0s, Zs, SPsos- This yields the characteristic impedances of the UEs and stubs
Z0s = 4.3489 0 4.3489Zs = -1.2986 -1.4052 -1.2986SPsos = 'Po' 'Po' 'Po' - With the +/− signs of Zs values standing for L/C or short‐/open‐circuited stubs, respectively, this implies the microstrip filter in Figure 7.17.2(c) where, say, Zs(1) = −1.2986 together with SPsos(1) = Po means that the first stub of characteristic impedance 1.2986 Ω is a parallel open‐circuited one and, say, Z0s(1) = 4.3489 means that the characteristic impedance of the UE next to the first stub is 4.3489 Ω.
- This yields the characteristic impedances of the UEs and stubs
- (Step 5) Denormalize the normalized characteristic impedances by multiplying them with Rs = 50 Ω:
>>Z0s=Z0s*Rs, Zs=Zs*Rs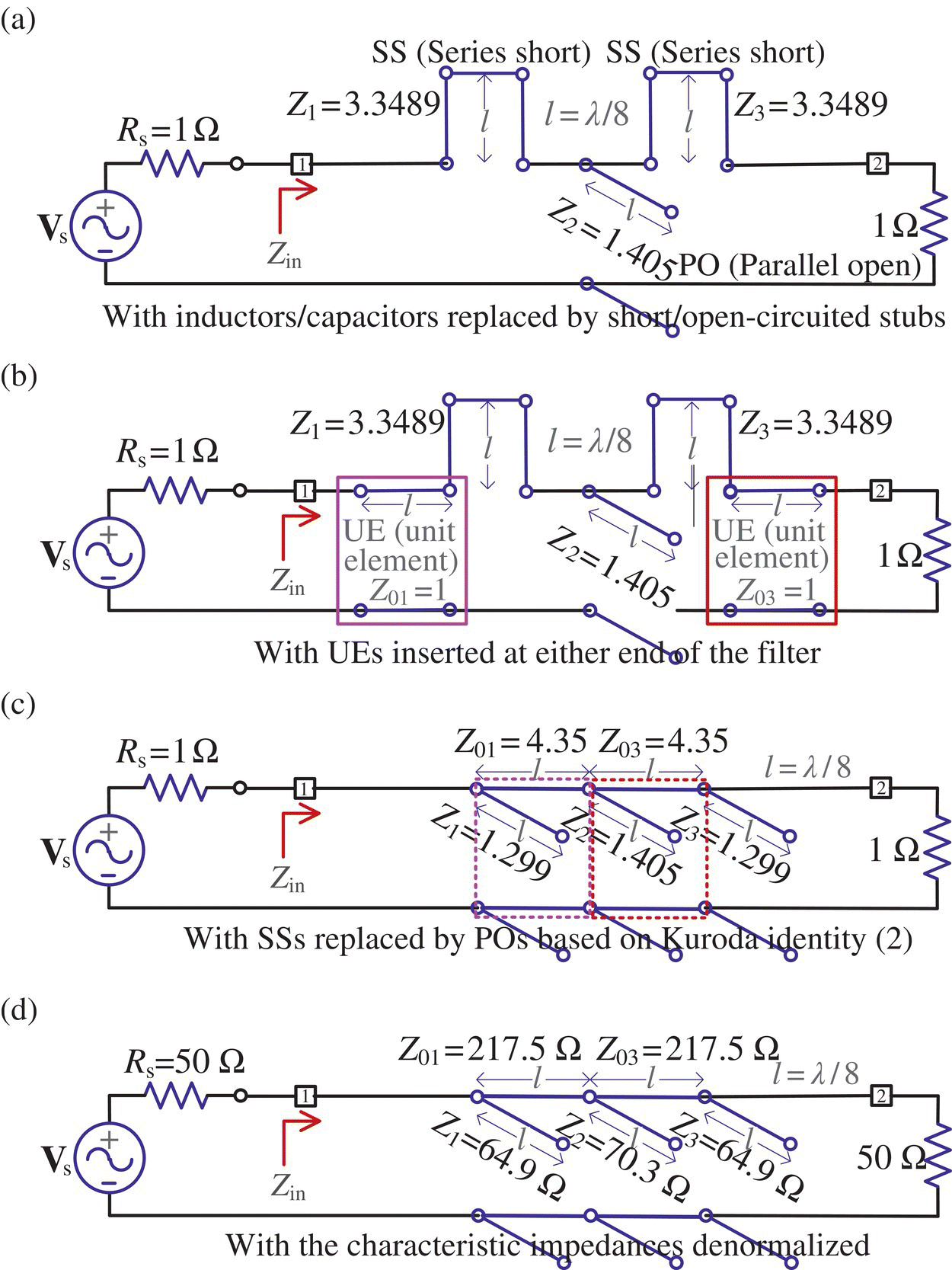
Figure 7.17.2 Microstrip filter design for Example 7.5.
- This yields
Z0s = 217.4466 0 217.4466Zs = -64.9301 -70.2575 -64.9301 - This implies the microstrip filter in Figure 7.17.2(d).
- This yields
- (Step 6) Frequency scale the circuit by determining the line/stub lengths as l = λ/8 = vp/fc/8[m] where vp[m/s] is the phase velocity of signal propagating on the line and fc is the cutoff frequency given as a design specification.
- (Step 7) To plot the frequency responses of the two filters, one (called a lumped‐element filter) consisting of lumped elements L/C (Figure 7.17.1) and the other (called a distributed‐element filter) consisting of microstrip lines/stubs (Figure 7.17.2(d)), we do the following:
- We first construct a vector of the characteristic impedances of each stub/line:
>>Z0strip=[Zs(1) Z0s(1) Zs(2) Z0s(3) Zs(3)];- and the corresponding cell
>>SPsos={SPsos{1} 'Tl' SPsos{2} 'Tl' SPsos{3}}; - which contains one of the five strings {‘Po’, ‘Tl’, ‘Po’, ‘Tl’, ‘Po’} for each stub/line depending on whether it is a parallel‐/series‐connected stub or a section of TL and also whether it is short‐ or open‐circuited if it is a stub.
- and the corresponding cell
- Referring to Eqs. (7.3.27) and (7.3.28), set the frequency range which to plot the frequency response for:
>>l=1/8; fc=4e9; % Stub length and Cutoff frequencyfN=linspace(0,pi/4,1000); % Normalized frequency rangew=fN*2*pi*fc; % Real frequency rangebl=2*pi*w*l/fc; % Range of bl (bl=2*pi*l at f=fc=4e9[Hz]) - To get the overall frequency response considering Rs, we use the MATLAB function ‘
GZ_strip()’ to get the frequency response G(ω) (Gw) and input impedance Zin(ω) (Zinw) of the filter (excluding Rs) for the frequency range set above:>>ZL=Rs; [Gw,Zinw]=GZ_strip(Z0strip,SPsos,ZL,bl);
- and we multiply G(ω) with the voltage divider ratio Zin(ω)/(Rs+Zin(ω)) on the source side:
>>Gw=Zinw./(Rs+Zinw).*Gw; % the overall frequency response - Here, the below MATLAB function ‘
GZ_strip()’ is supposed to be saved on the computer.
function [Gw,Zinw]=GZ_strip(Z0strip,SPsos,ZL,bl)% To get the frequency response Gw and input impedance Zinw% Input:% Z0strip = Impedances of stub, line, stub, line, ...% SPsos = e.g. {'Ss','Po',..} for Series-short, Parallel-open, ..% ZL = Load impedance% bl = Range of electrical length% Output:% Gw = Frequency response% Zinw = Input AC impedanceZl=@(ZL,Z0,bl)(ZL+j*Z0*tan(bl))./(Z0+j*ZL.*tan(bl))*Z0;% Impedance of a line of characteristic impedance Z0 and% electrical length bl with load ZLZls=@(Z0,bl)j*Z0*tan(bl); % Impedance of a an SSZlo=@(Z0,bl)-j*Z0./tan(max([bl; eps*ones(1,numel(bl))]));% Impedance of an open-circuited stubZlso=@(Z0,bl,so)(so=='s')*Zls(Z0,bl)+(so=='o')*Zlo(Z0,bl);Z_par=@(Z1,Z2)Z1.*Z2./(Z1+Z2); % Parallel(shunt) combinationZ0strip=abs(Z0strip); Zinw=ZL; I=1;for m=numel(Z0strip):-1:1if isempty(SPsos{m})|Z0strip(m)<eps, continue; endSP=upper(SPsos{m}(1)); so=lower(SPsos{m}(2));if SP=='P'Zp=Z_par(Zlso(Z0strip(m),bl,so),Zinw); % Parallel combinationI=I.*Zinw./Zp; Zinw=Zp; % Sum of shunt currents.elseif SP=='S'Zinw=Zinw+Zlso(Z0strip(m),bl,so); % Series combinationelseif SP=='T', Zinw=Zl(Zinw,Z0strip(m),bl); % Serial lineendendGw=ZL./(Zinw.*I); % Ratio of voltage across ZL to Input voltage
- To plot the magnitudes [dB] of the overall frequency responses considering Rs (with maximum of 0 dB) for the two filters, we run the following MATLAB statements:
>>Gwmag=20*log10(max(abs(Gw),1e-5));clf, plot(w,Gwmag-max(Gwmag)), hold ons=j*w/fc; Gw0=eval(Gs); Gwmag0=20*log10(max(abs(Gw0),1e-5));plot(w,Gwmag0-max(Gwmag0),'r') % To make the maximum 0dB- where Gs is the transfer function obtained in Step 2. This yields Figure 7.17.3.
An easy alternative to implement an LC ladder using stubs is a stepped‐impedance or hi‐Z, low‐Z filter [P-1] obtained by replacing the normalized values of inductance L and capacitance C with TL sections of high/low characteristic impedances Zh/Zl and electrical lengths
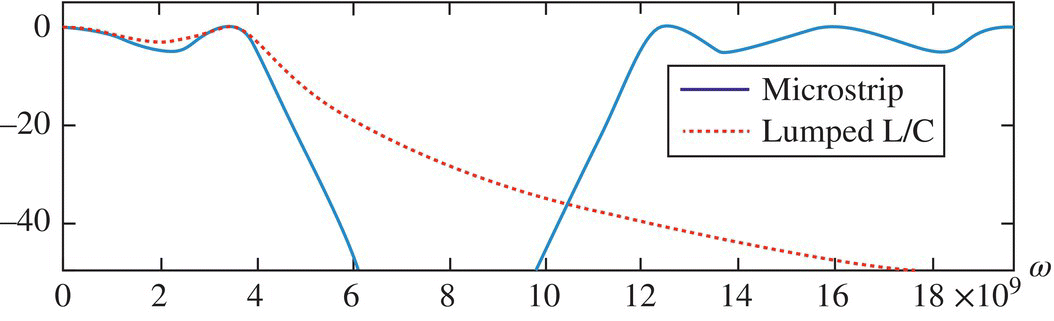
Figure 7.17.3 Frequency responses of the lumped‐element filter and distributed‐element filter.
(7.3.35b)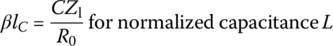
- respectively.
Example 7.6 Design of Stepped‐Impedance Filter [P-1]
For line/load impedances R0 = 50 [Ω]/ZL = 50 [Ω], design a sixth‐order Butterworth LPF prototype with passband ripple Rp = 3 dB and implement it as a stepped‐impedance filter with Zh = 150 [Ω] and Zl = 10 [Ω].
To design such an LPF, we run the following MATLAB script “elec7e06.m”
%elec07e06.m: Butterworth LPF design in Example 8.7 of [P-1]N=6; Rp=3; % Order and Passband ripple of Butterworth LPFtype='B'; % Butterworthgg=LPF_ladder_coef(N,type,Rp)% To find the L & C values of the prototype Pi filterR0=50; Rs=R0; pT='pi'; wc=1; % for a prototype filter[LCRs,LCRs_,Gs]=LC_ladder(Rs,gg,pT,wc);disp('Values of the lumped elements L, C, and RL')format short e; LCRs, LCRs_LCs=LCRs(1:N); LCs_=LCRs_(1:N);Zh=150; Zl=10; % Highest/lowest practical line impedancesbl=@(g,LC_)(LC_=='L')*g*R0/Zh+(LC_=='C')*g*Zl/R0; % Eq. (7.3.35a,b)Z0=@(LC_)(LC_=='L')*Zh+(LC_=='C')*Zl;% Find the electrical lengths of the hi/low-Z transmission line sections% to replace the series inductors and shunt capacitors.for m=1:Nbls(m)=bl(gg(m),LCs_{m}(1)); Z0s(m)=Z0(LCs_{m}(1));enddisp('Electrical lengths, Characteristic impedances of microstrip lines')Z0s, Els=rad2deg(bls) % Characteristic impedances, Electrical lengths
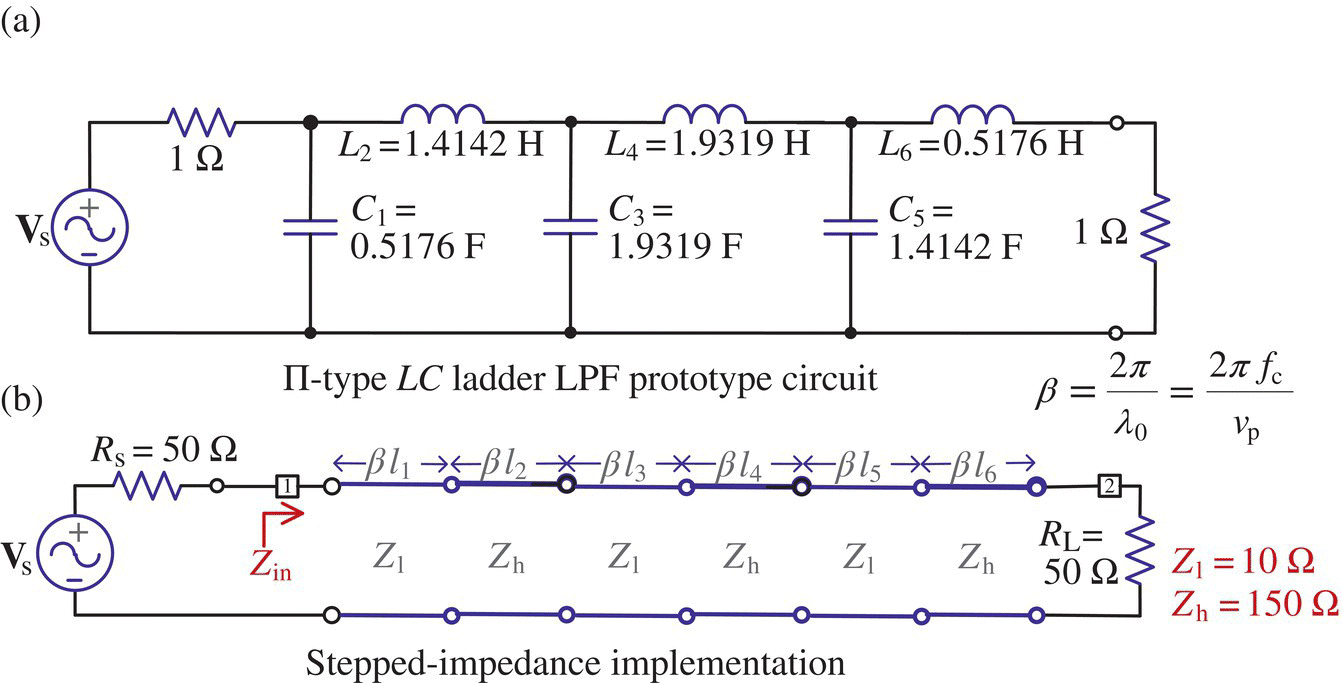
Figure 7.18 Sixth‐order Butterworth 3 dB LPF realized with a П‐type LC ladder and implemented as a stepped‐impedance filter.
to get the electrical lengths and characteristic impedances of each TL section as
Z0s = 10 150 10 150 10 150ELs = 5.9317 2.7009 2.2137 3.6896 1.6206 9.8862
This means the stepped‐impedance LPF of Figure 7.18(b).
7.3.6 Impedance Matching with Lumped Elements
This section presents several examples illustrating how some types of impedance matchers consisting of lumped elements can be designed by using the Smith chart.
Example 7.7 Design of L‐type Impedance Transformers Using the Smith Chart
Find L‐type LC circuits transforming the impedance Z1 = 40 + j50[Ω] or admittance Y1 = 1/Z1 = 0.009756 − j0.012195 [S] represented by point Γ1 into the impedance Z2 = 50 + j17 [Ω] or Y2 = 1/Z2 = 0.017928 − j0.060954 [S] (so that it can be matched to Zs = 50 − j17 [Ω]) by using the Smith chart and compare the results with those obtained in Example 6.12.
Noting that there are four paths along resistance/conductance curves from point Γ1 (representing Z1 = 40 + j50 [Ω]) to Γ2 (representing Z2 = 50 + j17 [Ω]), each via Γ3, Γ5, Γ6, and Γ7 in Figure 7.13, let us work with ‘Smith V4.1’ taking the following steps:
- From the top menu bar, select Tools > Settings to open the Settings dialog box, set the values of Z0 (characteristic impedance) and frequency to 50 [Ω] (default) and 1 [GHz], respectively, and click OK button. In fact, as long as the design objective is not to match the input impedance with the characteristic impedance, it does not matter whatever value Z0 is set to, because ‘Smith V4.1’ accommodates even unnormalized impedances/admittances as they are.
- From the toolbar (below the menu bar), select Keyboard to open Data Point dialog box, insert the impedance Z1 = 40
+j50 [Ω] as a (start) point (DP1), and click OK button. Also, insert Z2 = 50+j17 [Ω] as a (target) point (DP2). If you want to cancel (undo) any work or delete the data points starting from the last one (in LIFO order), just right‐click anywhere on the Smith chart. - To design the L1‐type C‐C impedance matcher as shown in Figure 6.19(a1) corresponding to the path from Γ1 to Γ2 via Γ3, click on ‘Insert series capacitor’ button and move the mouse cursor to click on Γ3 (the intersection of the R = 40 Ω‐circle and G = 0.0179 S‐circle) at which the value of G = Re{Y} is close to 0.0179 S = 17.9 mS as can be read in the Cursor pane. Then, TP 3 will appear at Γ3 and its impedance value will appear in the Data Points pane at the right side as shown in Figure 7.19.
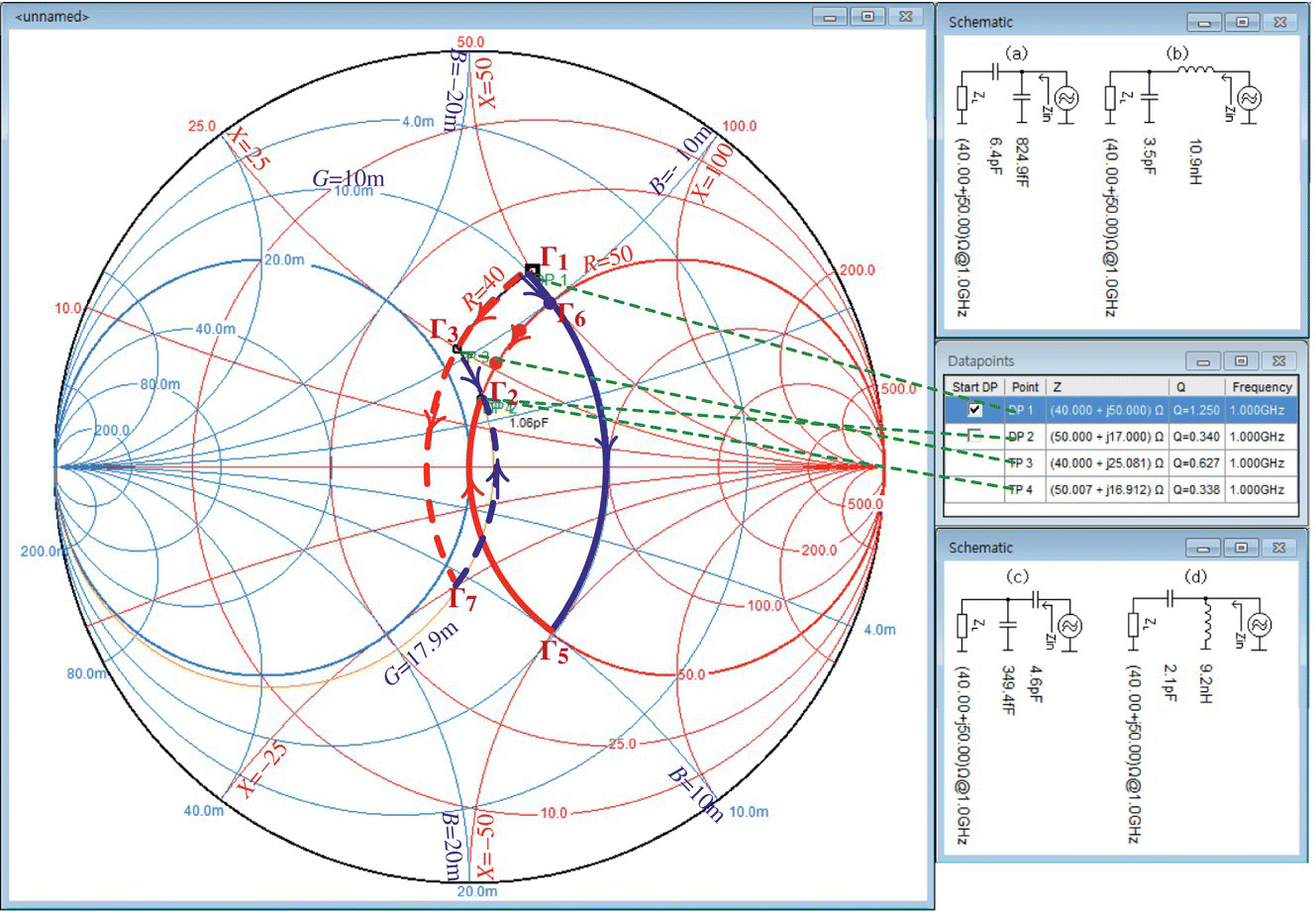
Figure 7.19 Using ‘Smith 4.1’ to design L‐type impedance matchers in Example 7.7 or 6.12.
- From the tool bar, click on ‘Insert parallel capacitor’ button and move the mouse cursor to click on Γ2 (the intersection of the R = 50 Ω‐circle and the G = 17.9 mS‐circle) representing Z2 = 50
+j17 [Ω]. Then, TP 4 will appear at Γ2 and its impedance value will appear in the Data Points pane. - Then, the designed network with the parameter values C2 = 6.4 pF and C1 = 824.9 fH will be shown in the Schematic pane at the upper‐right part of the window. It conforms with Figure 6.19(a1).
- If you want to read more digits of a numeric value or change it, double‐click on it to open the Edit Element dialog box.
- Right‐click anywhere on the Smith chart twice to delete the last two data points.
- To design the L2‐type L‐C impedance matcher as shown in Figure 6.19(b1) corresponding to the path from Γ1 to Γ2 via Γ5, click on ‘Insert parallel capacitor’ button (from the tool bar) and move the mouse cursor to click on Γ5 (the intersection of the G=0.009756 S ≈ 0.01 S‐circle and the R=50 Ω‐circle) at which the value of R=Re{Z} is close to 50 Ω as can be read in the Cursor pane.
- From the tool bar, click on ‘Insert series inductor’ button and move the mouse cursor to click on Γ2 (the intersection of the R=50 Ω‐circle and the X=17 Ω‐circle) representing Z2=50
+j17 [Ω]. - Then, the designed network with the parameter values C2 = 3.5 pF and L1 = 10.9 nH will be shown in the Schematic pane at the upper‐right part of the window. It conforms with Figure 6.19(b1).
Example 7.8 Design of T‐type Impedance Transformers Using the Smith Chart
Make T‐type ladders with quality factor Q = 3 for transforming Z1 = 60 − j30 [Ω] to Z2 = 10 + j20 [Ω] at frequency fc = 1 GHz.
Note that, with Q ≤ 3, there are four paths along resistance/conductance curves from point Γ1 (representing Z1=60 − j30[Ω]) to Γ2 (representing Z2=10+j20[Ω]), each via Γ5‐Γ3, Γ5‐Γ4, Γ6‐Γ4, and Γ6‐Γ3, in Figure 7.20 where Γ3 and Γ4 have been determined as the intersections between 10 Ω‐resistance circle and Q= 3‐circles. Let us work with ‘Smith V4.1’ taking the following steps:
- From the top menu bar, select Tools > Circles to open the Circles dialog box, insert 3 as a value of Q, and click OK to close the dialog box so that two Q=3‐circles appear above/below the real axis.
- From the top menu bar, select Tools > Settings to open the Settings dialog box, set the values of Z0 and frequency to 50[Ω] (default) and 1[GHz], respectively, and click OK.
- From the toolbar, select Keyboard to open Data Point dialog box, insert Z1 = 60 − j30[Ω] as a (start) point (DP1), and click OK. Also, insert Z2=10
+j20[Ω] as a (target) point (DP2). See Figure 7.20.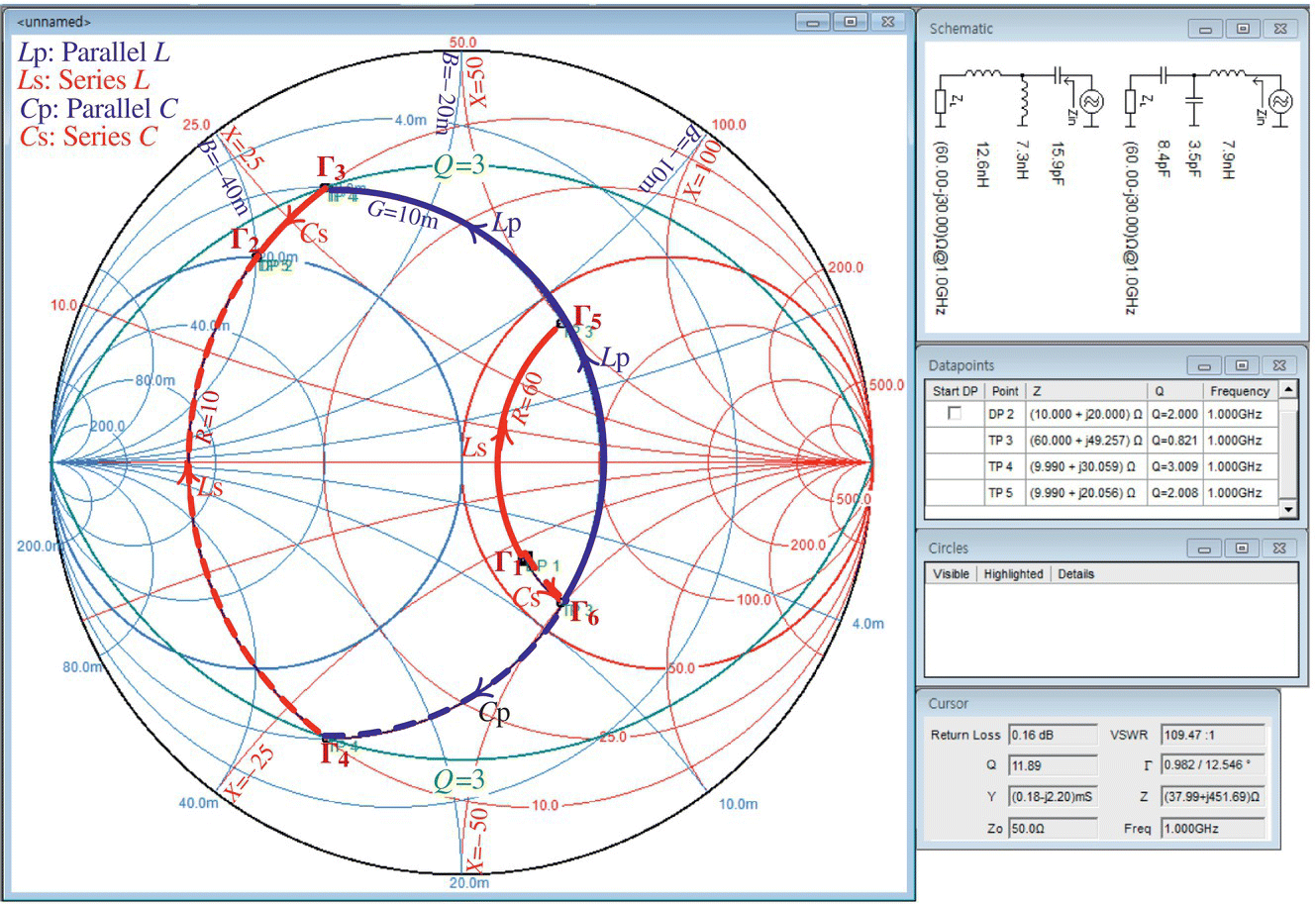
Figure 7.20 Using ‘Smith 4.1’ to design T‐type impedance matchers in Example 7.8 or 6.13.
- To designate Γ3 and Γ4 as intermediate points just before the target point Γ2, click on the ‘Mouse’ button, find two points with R = R2 = 10[Ω] and Q = 3, one by one, on the two Q=3‐circles (keeping your eye on the values of Q and R = Re{Z} in the Cursor pane), and click on them to insert as data points. In fact, noting that the R‐value of (the resistance circle through) Γ2 is 10 [Ω], we can compute the X‐value of (the reactance circle through) Γ3 with Q = 3 as
(E7.8.1)
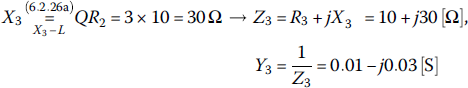
- Noting that the number of data points is not allowed to exceed 5, designate Γ5 as an intermediate point by clicking on a point with G5 = G3 = 10 [mS] (equal to the conductance value of Γ3) and R5 = R1 = 60 [Ω] (equal to the resistance value of Γ1) (keeping your eye on the values of R = Re{Y} and G = Re{Y} in the Cursor pane) to insert it. Why is that? Because we are going to connect the reactive elements (each corresponding to the Γ1‐Γ5 and Γ5‐Γ3 sections, respectively) in series and in parallel, respectively. In fact, from R5 = 60 Ω and G5 = 0.01 S, we can compute the X5 for Γ5 as
or
>>R5=60; G5=0.01; [Z5,Y5]=RG2ZY(R5,G5) % see Problem 7.9 - To design the T‐type C‐L‐L impedance matcher as shown in Figure 6.22(a) corresponding to the path from Γ1 to Γ2 via Γ5‐Γ3, click on ‘Insert series inductor’ and move the mouse cursor to click on Γ5 (corresponding to Z5=60
+j49[Ω]). Then, click on ‘Insert parallel inductor’ and move the mouse cursor to click on Γ3 (corresponding to Z3 = 10+j30 [Ω]). Then, click on ‘Insert series capacitor’ and move the mouse cursor to click on Γ2 (corresponding to Z2=60− j30[Ω]). Then, the designed network appears in the Schematic pane as shown in Figure 7.20 where L3 = 12.61 nH, L2 = 7.306 nH, and C1 = 15.91 pF. - To design the T‐type L‐C‐C impedance matcher as shown in Figure 6.22(d) corresponding to the path from Γ1 to Γ2 via Γ6‐Γ4, click on ‘Insert series capacitor’ and move the mouse cursor to click on Γ6 (corresponding to Z6=60− j49[Ω]). Then, click on ‘Insert parallel capacitor’ and move the mouse cursor to click on Γ4 (corresponding to Z4 = 10 − j30 [Ω]). Then, click on ‘Insert series inductor’ and move the mouse cursor to click on Γ2. Then, the designed network appears in the Schematic pane (Figure 7.20) where C3 = 8.383 pF, C2 = 3.488 pF, and L1 = 7.945 nH.
Example 7.9 Design of П‐type Impedance Transformers Using the Smith Chart
Make П‐type ladders with quality factor Q = 2 for transforming Z1 = 10 − j10 [Ω] to Z2=20+j40[Ω] at frequency fc = 2.4 GHz.
Note that, with Q ≤ 2, there is a path along resistance/conductance curves from point Γ1 (representing Z1 = 10 − j10 [Ω] or equivalently Y1 = 50 + j50 [mS]) to Γ2 (representing Z2=20+j40[Ω] or equivalently Y2=10+j20[mS]) via Γ3‐Γ4 in Figure 7.21 where Γ4 has been determined as the intersection between G = 10 mS‐circle and the lower Q = 2‐circle. Let us work with ‘Smith V4.1’ taking the following steps:
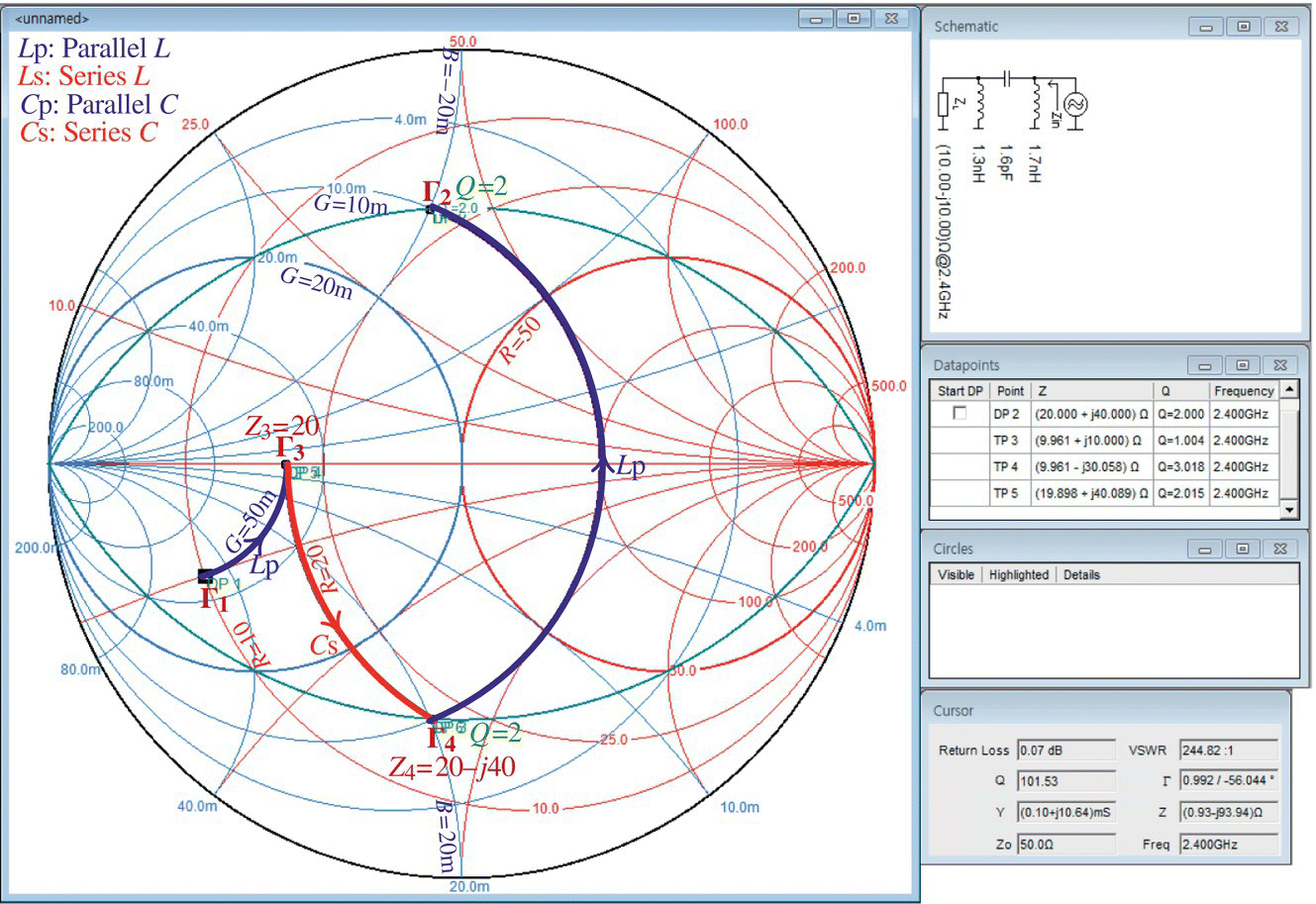
Figure 7.21 Using ‘Smith 4.1’ to design П‐type impedance matchers in Example 7.9 or 6.14.
- From the top menu bar, select Tools > Circles to open the Circles dialog box, insert 2 as a value of Q, and click OK to close the dialog box so that two Q = 2‐circles appear above/below the real axis.
- From the top menu bar, select Tools > Settings to open the Settings dialog box, set the values of Z0 and frequency to 50[Ω] (default) and 2.4[GHz], respectively, and click OK.
- From the toolbar, select Keyboard to open Data Point dialog box, insert Z1=10 − j10[Ω] as a (start) point (DP1), and click OK. Also, insert Z2 = 20
+j40 [Ω] as a (target) point (DP2). See Figure 7.21. - To set an intermediate point Γ4 just before the target point Γ2, click on the ‘Mouse’ button, find a point with G = G2 = 10[mS] and Q = 2 on the lower Q = 2‐circle (keeping your eye on the values of Q and G = Re{Y} in the Cursor pane), and click on it to insert as data points. Why not on the upper Q=2‐circle? Because Γ2 is on the upper Q=2‐circle. In fact, noting that the G‐value of (the G‐circle through) Γ2 is 0.01[S], we can compute the B‐value of (B‐circle through) Γ4 with Q = 2 as
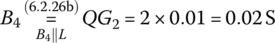
This implies that the admittance and impedance for Γ4 are
(E7.9.1)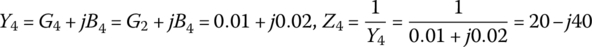
Why have we set G4 = G2? Because we are going to connect the reactive element (corresponding to the Γ4‐Γ2 section) in parallel with Z2, as denoted by ‘Lp’.
- To determine another intermediate point Γ3 (between Γ1 and Γ4), we set the conductance and resistance to 50 mS (that for Γ1) and 20 Ω (that for Γ4), respectively, because we are going to connect the reactive elements (each corresponding to the Γ1‐Γ3 and Γ3‐Γ4 sections, respectively,) in parallel and in series, respectively:
(E7.9.2)
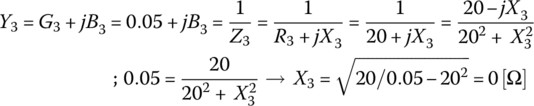
or
>>R3=20; G3=0.05; [Z3,Y3]=RG2ZY(R3,G3)If you somehow have got the numeric value of the Z, Y, or Γ of a data point to be inserted, you can select Keyboard to open the Data Point dialog box and enter the value.
- To design the П‐type L‐C‐L impedance matcher as shown in Figure 6.23(b) corresponding to the path from Γ1 to Γ2 via Γ3‐Γ4, click on ‘Insert parallel inductor’ and move the mouse cursor to click on Γ3 (corresponding to Z3 = 20
+j0 [Ω]). Then, click on ‘Insert series capacitor’ and move the mouse cursor to click on Γ4 (corresponding to Z4=20 − j40[Ω]). Then, click on ‘Insert parallel inductor’ and move the mouse cursor to click on Γ2 (corresponding to Z2 = 20+j40 [Ω]). Then, the designed network appears in the Schematic pane as shown in Figure 7.22 where(E7.9.3)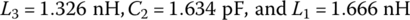
Regrettably, this design result is quite different from that of Figure 6.23(b). To figure out the difference between the design result using the Smith chart and that using the MATLAB function ‘
imp_matcher_pi()’, we have drawn the latter on the Smith chart in Figure 7.22, which shows that some intermediate points such as Γ4 and Γ6 do not satisfy the upper bound condition for Q. It implies that the design result using the Smith chart satisfies the Q‐condition at every stage while that using MATLAB may not satisfy the Q‐condition at some stage even if both design results satisfy the condition as a whole.
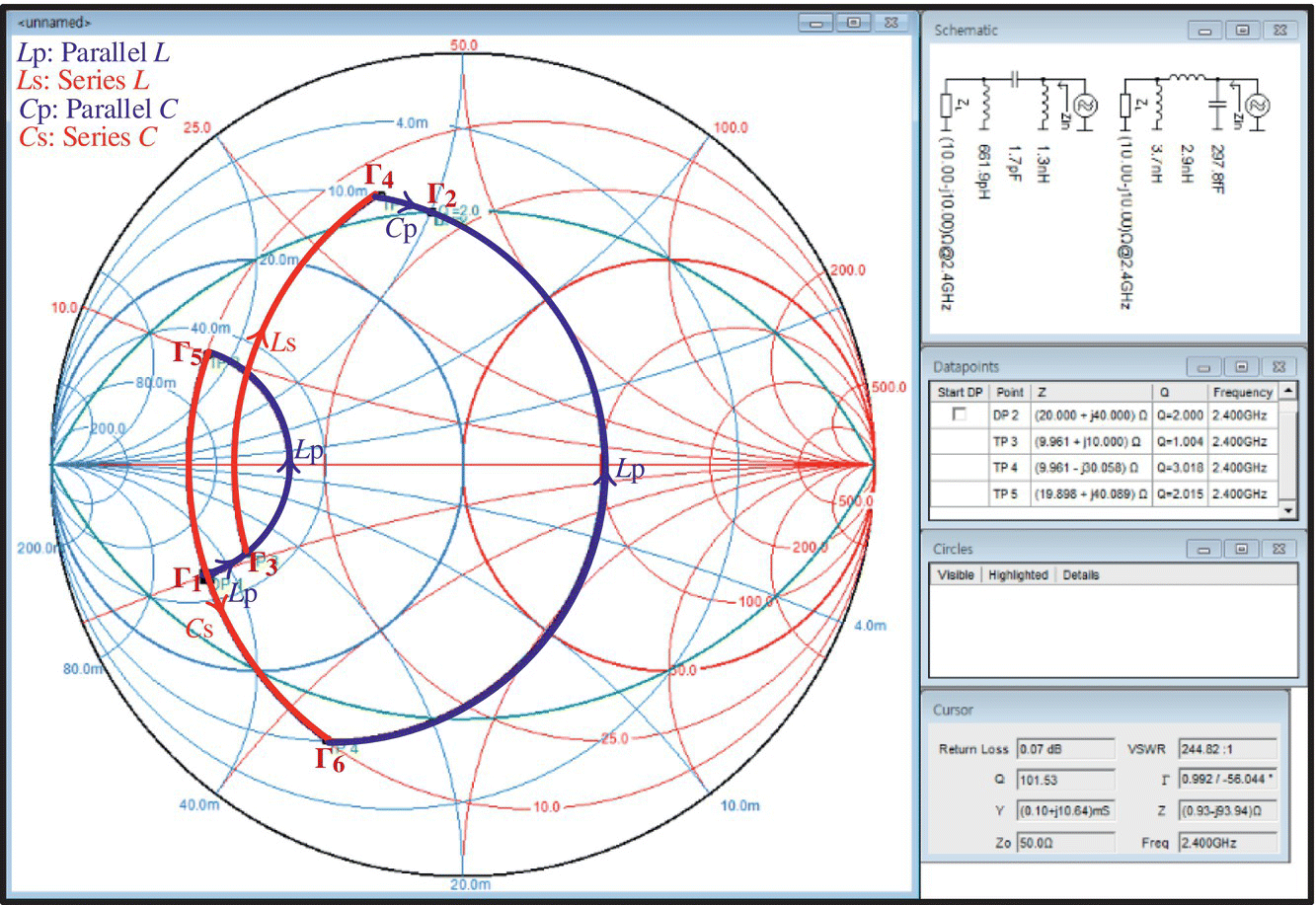
Figure 7.22 The design results of Figure 6.23(b) and (d) (Example 6.14) drawn on the Smith chart.
Example 7.10 Impedance Matching with an LC Ladder
Make LC ladder‐type impedance matchers (with quality factor Q ≤ 1 at every stage) for transforming Z1=12.5+j10[Ω] to 50 Ω at frequency fc=100 MHz.
- Let us work with ‘Smith V4.1’ taking the following steps to make an LPF LC ladder‐type impedance matcher:
- From the top menu bar, select Tools > Circles to open the Circles dialog box, insert 1 as a value of Q and click OK to close the dialog box so that two Q=1‐circles appear above/below the real axis.
- From the top menu bar, select Tools > Settings to open the Settings dialog box, set the values of Z0 and frequency to 50 [Ω] (default) and 100 [MHz], respectively, and click OK.
- From the toolbar, click on ‘Keyboard’ to open Data Point dialog box, insert the impedance Z1 = 12.5
+j10 [Ω] or Y1 = 48.8+j39 [mS] as a (start) point (DP1), and click OK. The target point Γ = 0, i.e. the origin corresponding to Z0 = 50 [Ω], is so apparent that it does not have to be designated as a data point.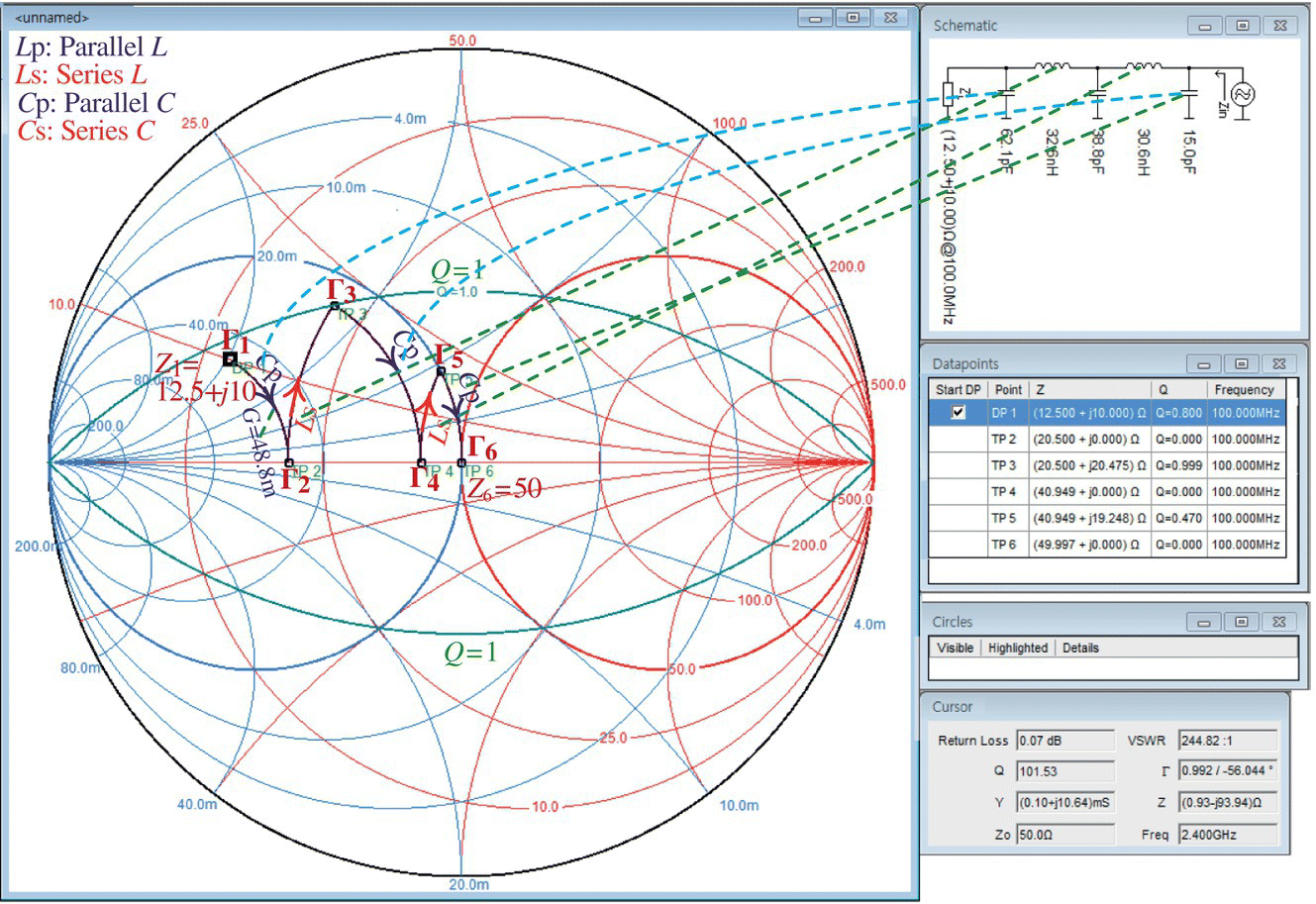
Figure 7.23 Using ‘Smith 4.1’ for impedance matching between Z1 = 12.5
+j10 and Z6 = 50 in Example 7.10(a). - To design an LC ladder‐type impedance matcher as an LPF, take the following steps, referring to Figure 7.23:
- Click on ‘Insert parallel capacitor’ and move the mouse cursor to click on Γ2 (the intersection of G = G1 = 48.8 [mS]‐circle and the horizontal axis).
- Click on ‘Insert series inductor’ and move the mouse cursor to click on Γ3 (the intersection of R = R2 = 1/G1 = 20.5[Ω]‐circle and the upper Q = 1‐circle corresponding to Y3 = G3
+jB3[S]). - Click on ‘Insert parallel capacitor’ and move the mouse cursor to click on Γ4 (the intersection of G=G3‐circle and the horizontal axis).
- Click on ‘Insert series inductor’ and move the mouse cursor to click on Γ5 (the intersection of R=R4=1/G3‐circle and the G=1/R0‐circle).
- Click on ‘Insert parallel capacitor’ and move the mouse cursor to click on Γ6 = 0 (i.e. the origin corresponding to Z0 = 50[Ω]).
- Then, the designed LC ladder appears in the Schematic pane in Figure 7.23.
function Xs=imp_matcher_LC_LPF1(R0,ZL,fc,Qm)% Design an LC ladder LPF with Q<=Qm to make impedance matching with R0% when RL<R0% Copyleft: Won Y. Yang, [email protected], CAU for academic use onlyEPS=1e-4;if abs(ZL-R0)<EPS, Xs=[]; return; endRL=real(ZL); XL=imag(ZL); YL=1/ZL; GL=real(YL); BL=imag(YL);if abs(XL)<EPSM1=abs(Qm); M2=sqrt(R0/RL-1);% Does the R-circle cross G=1/R0-circle or Q-circle first?[X,imin]=min([M1 M2]); X=X*RL;Z=RL+j*X; Y=1/Z; B=imag(Y);if abs(M1-M2)<EPS|imin>1 % If it crosses G=1/R0-circle firstXs=[1/B X]; % Series L & Parallel C from Loadelse % If it crosses Q-circle firstRL=1/real(Y); Xsp=imp_matcher_LC_LPF1(R0,RL,fc,Qm);Xs=[Xsp 1/B X]; % Series L & Parallel Cendelseif XL>0 % First, C in parallel with ZL for LPFRL=1/GL;Xsp=imp_matcher_LC_LPF1(R0,RL,fc,Qm);Xs=[Xsp 1/BL]; % Parallel Celse % if XL<0% Move the point from the 3rd quadrant into the 2nd one by Ls (series L).M1=abs(Qm); M2=sqrt(R0/RL-1);[X,imin]=min([M1 M2]); X=X*RL;Z=RL+j*X; Y=1/Z; B=imag(Y);if abs(M1-M2)<EPS|imin>1Xs=[1/B (X-XL)]; % Series L and Parallel C from LoadelseR=1/real(Y); Xsp=imp_matcher_LC_LPF1(R0,R,fc,Qm);Xs=[Xsp 1/B (X-XL)]; % Series L and Parallel Cendend
function [LCs,LCs_]=L_or_C_from_X(Xs,fc,vh)% vh = 'v' or 'h' for vertical/parallel or horizontal/series first% Find L or C from given values of reactance.% Copyleft: Won Y. Yang, [email protected], CAU for academic use onlywc=2*pi*fc;for n=1:length(Xs)X=Xs(n);if abs(X)<eps|abs(X)>realmax, LCs(n)=0; LCs_{n}='????';elseif X>0, LCs(n)=X/wc; LCs_n='L'; unit='H';else LCs(n)=-1/X/wc; LCs_n='C'; unit='F';endif nargin>2LCs_n=[LCs_n '(' vh ')'];if vh=='v', vh='h';else vh='v';end % To alternate 'L' and 'C'else fprintf([LCs_n '(%d)=%10.3e[' unit '] '],n,LCs(n));endLCs_{n}=LCs_n;endend
- This LPF LC ladder‐type impedance matcher (with quality factor Q ≤ 1 at every stage) can also be designed by using the above MATLAB function ‘
imp_matcher_LC_LPF1()’ as follows:>>fc=1e8; Qm=1; % Frequency and Maximum quality factorXs=imp_matcher_LC_LPF1(50,12.5+10i,fc,Qm)[LCs,LCs_]=L_or_C_from_X(Xs,fc,'v')LCs = 1.4913e-11 3.0573e-08 3.8818e-11 3.2627e-08 6.2109e-11LCs_= 'C(v)' 'L(h)' 'C(v)' 'L(h)' 'C(v)' - where the third input argument of ‘
L_or_C_from_X()’ has been given as'v'(meaning ‘vertical’) since we know that the last section of the path from Γ1 to Γ2 leads to a parallel C and consequently the first element of the LC ladder (from the source) is to be connected vertically. This design result conforms with that obtained using ‘Smith 4.1’ and shown in the Schematic pane in Figure 7.23.
- Now, to design an LC ladder‐type impedance matcher as a HPF, take the following steps:
- Right‐click anywhere on the Smith chart four times to delete the existing four data points Γ2, Γ3, Γ4, and Γ5 (in LIFO order) except Γ1.
- From the top menu bar, select Tools > Circles to open the Circles dialog box, insert 1 as a value of Q and click OK to close the dialog box so that two Q = 1‐circles appear above/below the real axis.
- From the top menu bar, select Tools > Settings to open the Settings dialog box, set the values of Z0 and frequency to 50[Ω] (default) and 100 [MHz], respectively, and click OK.
- From the toolbar, click on ‘Keyboard’ to open the Data Point dialog box, insert Z1=12.5
+j10[Ω] as a (start) point (DP1), and click OK. - To design an LC ladder‐type impedance matcher, do the following, referring to Figure 7.24:
- Click on ‘Insert series capacitor’ (from the tool bar) and move the mouse cursor to click on the point Γ2 (the intersection of R=R1=12.5[Ω]‐circle and the lower Q=1‐circle) corresponding to Y2=40
+j40[mS]. - Click on ‘Insert parallel inductor’ and move the mouse cursor to click on the point Γ3 (the intersection of G=G2=40[mS]‐circle and the horizontal axis).
- Click on ‘Insert series capacitor’ and move the mouse cursor to click on the point Γ4 (the intersection of R = 1/G3 = 1/0.04=25 Ω‐circle and the G=1/R0‐circle, which coincidentally happens to be on the lower Q = 1‐circle), corresponding to Y4=20
+j20 [mS].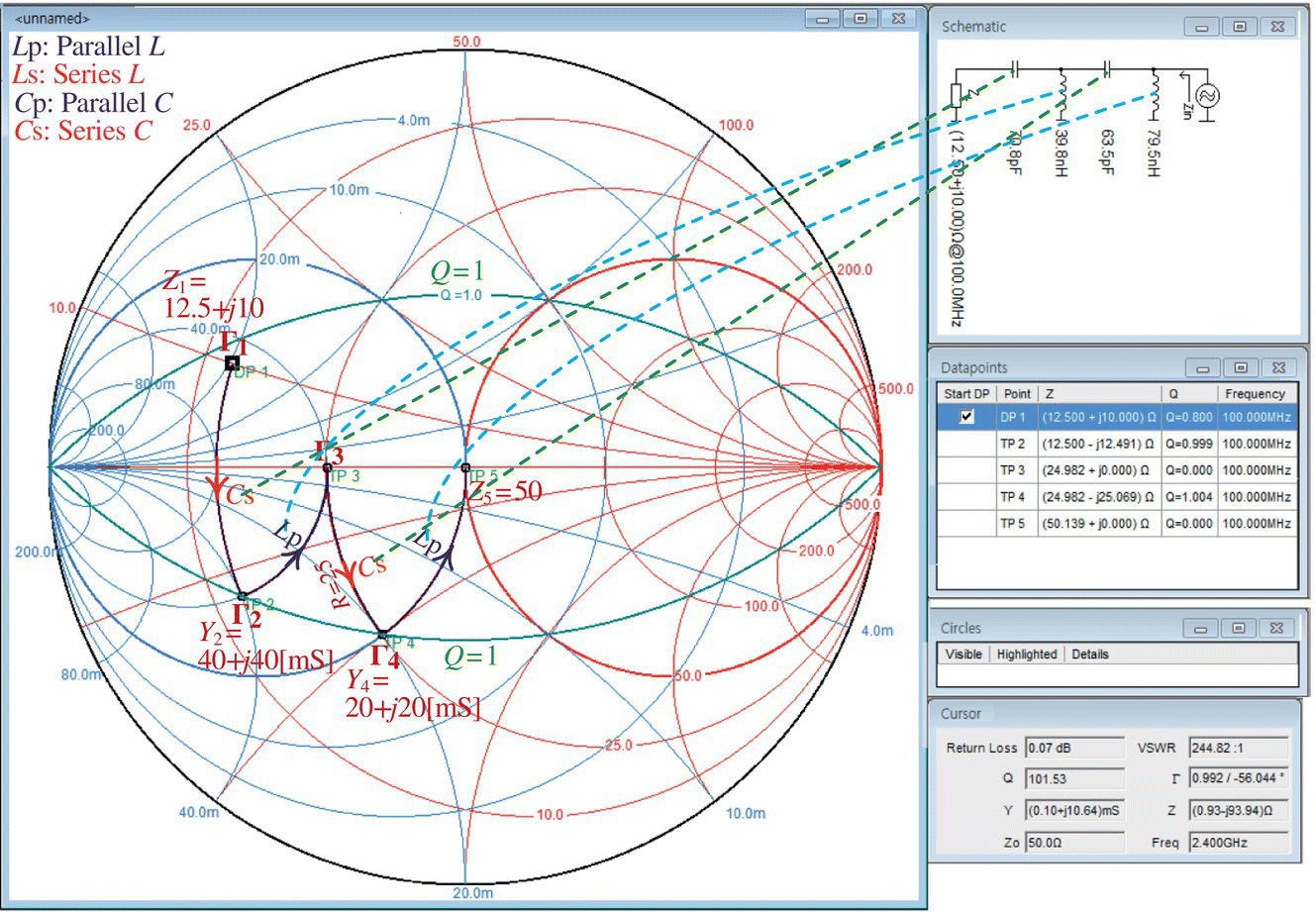
Figure 7.24 Using ‘Smith 4.1’ for impedance matching between Z1 = 12.5
+j10 and Z5 = 50 in Example 7.10(b). - Click on ‘Insert parallel inductor’ and move the mouse cursor to click on the point Γ5 = 0 (i.e. the origin corresponding to Z0 = 50 [Ω]).
- Click on ‘Insert series capacitor’ (from the tool bar) and move the mouse cursor to click on the point Γ2 (the intersection of R=R1=12.5[Ω]‐circle and the lower Q=1‐circle) corresponding to Y2=40
- Then, the designed LC ladder appears in the Schematic pane in Figure 7.24.
This HPF LC ladder‐type impedance matcher (with quality factor Q ≤ 1 at every stage) can also be designed by using the above MATLAB function ‘
imp_matcher_LC_HPF1()’ as follows:>>fc=1e8; Qm=1; % Frequency and Maximum quality factorformat short e; Xs=imp_matcher_LC_HPF1(50,12.5+10i,fc,Qm)[LCs,LCs_]=L_or_C_from_X(Xs,fc,'v')where the third input argument of ‘
L_or_C_from_X()’ has been given as'v'(meaning ‘vertical’) since we know that the last section of the path from Γ1 to Γ2 leads to a parallel L and consequently, the first element of the LC ladder (from the source) is to be connected vertically. Running these statements yields the following result:LCs = 7.9577e-08 6.3662e-11 3.9789e-08 7.0736e-11LCs_= 'L(v)' 'C(h)' 'L(v)' 'C(h)'This design result conforms with that obtained using ‘Smith 4.1’ and shown in the Schematic pane in Figure 7.24.
function Xs=imp_matcher_LC_HPF1(R0,ZL,fc,Qm)% Design an LC ladder HPF with Q<=Qm to make impedance matching with R0% when RL<R0% Copyleft: Won Y. Yang, [email protected], CAU for academic use onlyEPS=1e-4;if abs(ZL-R0)<EPS, Xs=[]; return; endRL=real(ZL); XL=imag(ZL); YL=1/ZL; GL=real(YL); BL=imag(YL);if abs(XL)<EPSM1=abs(Qm); M2=sqrt(R0/RL-1);% Does the R-circle cross G=1/R0-circle or Q-circle first?[X,imin]=min([M1 M2]); X=X*RL;Z=RL+j*X; Y=1/Z; B=imag(Y);if abs(M1-M2)<EPS|imin>1 % If it crosses G=1/R0-circle firstXs=[-1/B -X]; % Series C and Parallel L from Loadelse % If it crosses Q-circle firstRL=1/real(Y); Xsp=imp_matcher_LC_HPF1(R0,RL,fc,Qm);Xs=[Xsp -1/B -X]; % Series C and Parallel L from Loadendelseif XL<0 % First, L in parallel with ZL for HPFRL=1/GL; Xsp=imp_matcher_LC_HPF1(R0,RL,fc,Qm);Xs=[Xsp 1/BL]; % Parallel Lelse % if XL>0% Move the point from the 2nd quadrant into the 3rd one by Ls (series C).M1=abs(Qm); M2=sqrt(R0/RL-1);[X,imin]=min([M1 M2]); X=-X*RL;Z=RL+j*X; Y=1/Z; B=imag(Y);if abs(M1-M2)<EPS|imin>1 % If it crosses G=1/R0-circle firstXs=[1/B (X-XL)]; % Series C and Parallel L from Loadelse % If it crosses Q-circle firstR=1/real(Y); Xsp=imp_matcher_LC_HPF1(R0,R,fc,Qm);Xs=[Xsp 1/B (X-XL)]; % Series C and parallel Lendend%Usage:%fc=1e8; Qm=1; Xs=imp_matcher_LC_HPF1(50,10+5i,fc,Qm);%[LCs,LCs_]=L_or_C_from_X(Xs,fc,'v')
Example 7.11 Impedance Matching with Serial Line
Use a serial transmission line of characteristic impedance Z0 = 50 Ω and a parallel capacitor to make an impedance matching between ZL= 30 − j40[Ω] and 50 Ω at frequency fc = 430 MHz.
Having started ‘Smith V4.1’ to open the main window, take the following steps:
- From the top menu bar, select Tools > Settings to open the Settings dialog box, set the values of Z0 and frequency to 50[Ω](default) and 430[MHz], respectively, and click OK.
- From the toolbar, click on ‘Keyboard’ to open Data Point dialog box, insert the impedance ZL=30−j40[Ω] as a (start) point ΓL (DP1), and click OK. The target point Γ3 = 0, i.e. the origin corresponding to Z0 = 50 [Ω], is so apparent that it does not have to be designated as a data point.
- To design an impedance matcher consisting of a serial line and a reactive element C or L, you need to visualize a |Γ|‐circle centered at the origin and crossing ΓL (which shows the effect of a lossless SL [serial line] on the reflection coefficient Γ of the load impedance as described by Eq. (7.2.5)) and the G = 1/R0‐circle along which a Γ point can be moved by a parallel C or L to reach the target point Γ = 0, as have been shown in Figure 7.25. From Figure 7.25, notice that there are two intersections between the two circles, Γ2 and Γ4, each of which can be an intermediate point. Therefore, there are two paths from ΓL to the target point Γ3 = 0, one via Γ2 and one via Γ4.
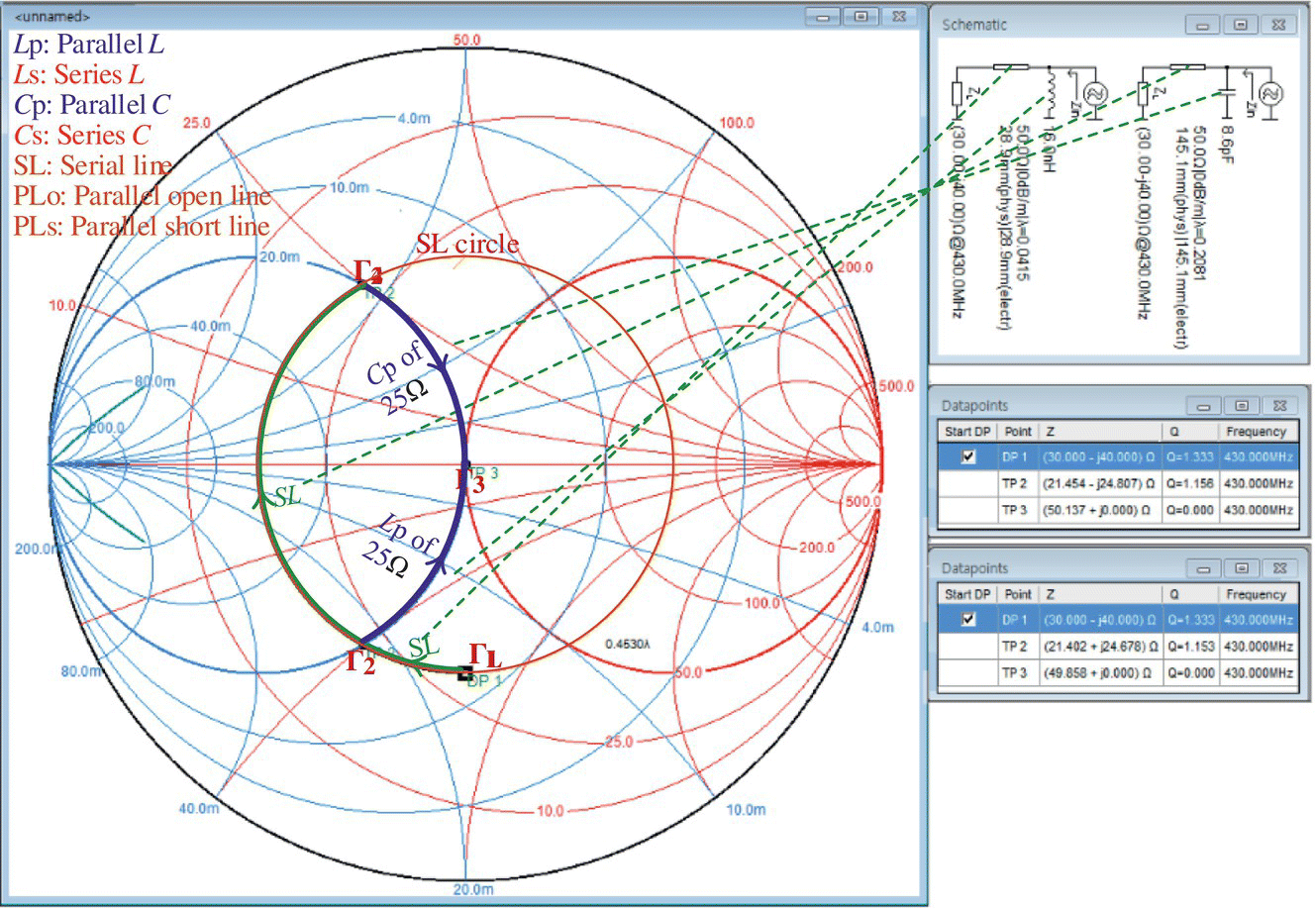
Figure 7.25 Using ‘Smith 4.1’ for impedance matching between ZL = 30 − j40 and Z6 = 50 in Example 7.11.
- First, to take the first path ΓL‐Γ2‐Γ3, do the following, referring to Figure 7.25:
- Click on ‘Insert serial line’ (from the tool bar) and move the mouse cursor to click on the point Γ2 (one intersection of the G = 1/R0‐circle and the |Γ|‐circle crossing ΓL).
- Click on ‘Insert parallel inductor’ and move the mouse cursor upward to click on the point Γ3 = 0 (i.e. the origin corresponding to Z0 = 50[Ω]).
- Then, the designed impedance matcher consisting of SL (serial line) and Lp (parallel inductor) appears in the Schematic pane as shown in Figure 7.25.
- Second, to take the second path ΓL‐Γ4‐Γ3, do the following:
- Click on ‘Insert serial line’ (from the tool bar) and move the mouse cursor to click on the point Γ4 (another intersection of the G = 1/R0‐circle and the |Γ|‐circle).
- Click on ‘Insert parallel capacitor’ and move the mouse cursor downward to click on Γ2 = 0.
- Then, the designed impedance matcher consisting of SL (serial line) and Cp (parallel capacitor) appears in the Schematic pane as shown in Figure 7.25.
As an alternative, we can compose the following MATLAB script “elec07e11.m” and run it to get
>>elec07e11ds = 0.0417 0.2083 % Transmission length(s)Xs = 24.7436 -24.7436 % Reactances to be adjustedL(1)= 1.603e-08[H] C(2)= 8.548e-12 - First, to take the first path ΓL‐Γ2‐Γ3, do the following, referring to Figure 7.25:
- These results conform with those obtained using ‘Smith 4.1’.
%elec07e11.mclear, clfZ0=50; b=2*pi; fc=430e6; ZL=30-40i; G0=1/Z0;[c,r]=Gcircle(G0,Z0); % Center and radius of the G-circle% To determine the length(s) of line to move from Gamma 1 to Gamma 2|4Zd=@(d)Z0*(ZL+j*Z0*tan(b*d))./(Z0+j*ZL*tan(b*d)); % Eq. (7.1.17)GammaZ=@(Z)(Z-Z0)./(Z+Z0); % Eq. (7.1.11)f=@(d)abs(GammaZ(Zd(d))-c)-r; % To be solved for the line length dds=[fsolve(f,0) fsolve(f,0.25)];ds=mod(ds,0.5) % Zd is periodic with period 0.5 in d[wavelength]Xs=1./(imag(1./Zd(ds)-1/Z0)) % Reactances to be adjusted for imp matchingLCs=L_or_C_from_X(Xs,fc);% To plot the G-circle, the Gamma-circle, and their intersectionsdth=0.01; ths=-pi+dth:dth:pi; ucircle=exp(j*ths);dd=[0:1e-4:0.5];plot(c+r*ucircle,'b'), hold on, plot(GammaZ(Zd(dd))+j*eps,'k')legend(['G=' num2str(G0,'%6.3e') '-circle'],'Line impedance effect')plot(GammaZ(Zd(ds)),'o'), axis('equal')
Problems
- 7.1 Skinship with the Smith Chart
To get familiar with the Smith chart, do the following:
- Compose the following MATLAB functions and save them as M‐files each named “G2Z.m” and “Z2G.m” if you don't have such similar M‐files.
function Z=G2Z(Gam,Z0)
if nargin<2, Z0=1; end
Z=Z0*(1+Gam)./(1‐Gam); %Eq. (7.2.1)function Gam=Z2G(Z,Z0)if nargin<2, Z0=1; endGam=(Z‐Z0)./(Z+Z0); %Eq. (7.2.3)- For the point Γ1 = 0.2
+j0.4 (with Z0 = 50) on the Smith chart in Figure 7.4, find the corresponding impedance/admittance and their normalized values, hopefully, by using one of the above MATLAB functions. Then, plot the point Γ1 and the R‐/X‐/G‐/B‐circles passing through Γ1 by completing and running the following MATLAB script “elec07p01b.m”.
%elec07p01b.mclear, clfZ0=50; Gam1=0.2+0.4i;Z1=???(Gam1,Z0), Y1=1/Z1 % Impedance and AdmittanceZ1n=Z1/Z0, Y1n=Y1*?? % Normalized impedance and admittanceths=pi/180*[0:360];plot(Gam1,'ro'), hold onR1=real(Z1); [cR1,rR1]=Rcircle(R1,Z0);plot(cR1+rR1*exp(j*ths)); % plot the R1-circleX1=imag(Z1); [cX1,rX1]=Xcircle(X1,Z0);plot(cX1+rX1*exp(j*ths),':'); % plot the X1-circleG1=real(Y1); [cG1,rG1]=Gcircle(G1,Z0);plot(cG1+rG1*exp(j*ths),'r'); % plot the G1-circleB1=imag(Y1); [cB1,rB1]=Bcircle(B1,Z0);plot(cB1+rB1*exp(j*ths),'r:'); % plot the B1-circleplot(exp(j*ths)); % plot the unit circle as backgroundplot([-1 1],[0 0],'k', [0 0],[-1 1],'k') % Horizontal/vertical axesaxis('equal'), axis([-1 1 -1 1])- For the point Γ2 = −0.2 − j0.4 (with Z0 = 50) on the Smith chart in Figure 7.4, find the corresponding impedance/admittance and their normalized values, hopefully, by using one of the above MATLAB functions. Then, plot the point Γ2 and the R‐/X‐/G‐/B‐circles passing through Γ2 by completing and running the following MATLAB script “elec07p01c.m”.
%elec07p01c.mZ0=50; Gam2=-0.2-0.4i;Z2=G2Z(Gam2,??), Y2=1/Z2 % Impedance and AdmittanceZ2n=Z2/??, Y2n=Y2*Z0 % Normalized impedance and admittanceplot(Gam2,'ro'), hold onR2=real(Z2); [cR2,rR2]=Rcircle(R2,Z0);plot(cR2+rR2*exp(j*ths)); % plot the R1-circleX2=imag(Z2); [cX2,rX2]=Xcircle(X2,Z0);plot(cX2+rX2*exp(j*ths),':'); % plot the X1-circleG2=real(Y2); [cG2,rG2]=Gcircle(G2,Z0);plot(cG2+rG2*exp(j*ths),'r'); % plot the G1-circleB2=imag(Y2); [cB2,rB2]=Bcircle(B2,Z0);plot(cB2+rB2*exp(j*ths),'r:'); % plot the B1-circle- For the points Γ1 = 0.2
+j0.4 and Γ2 = −0.2 − j0.4 (with Z0 = 50), find the corresponding impedance/ admittance and their normalized values by using the Smith Chart software ‘Smith V4.1’ - Which one of the circles drawn in (b) can the Γ‐point move from Γ1 to Γ=0 along? Which one of the circles drawn in (c) can the Γ‐point move from Γ = 0 to Γ2 along?
- Find the Γ‐points for Z3 = 25
+j25 (with Z0 = 50) and Y4 = 0.01+j0.01 (with Z0 = 50).
- 7.2 Using the Smith Chart
In connection with Example 7.1, find two L‐type LC circuits transforming the normalized impedance Z1=1
+j1[Ω] or admittance Y1=1/Z1=0.5 − j0.5 [S] represented by point Γ1 into the normalized impedance Z2 = 0.5 − j0.5 [Ω] represented by point Γ2, one via Γ4 and the other via Γ0 = 0 on the Smith chart in Figure 7.4. - 7.3 Single‐Stub Shunt Impedance Matching
Consider the single‐stub shunt impedance matching discussed in Section 7.3.2.1 to find the distance (from the load) and length of shunt single stub so that they can match a given load impedance ZL to the lossless transmission (or feed) line of characteristic impedance Z0.
- Misra [M-2] presents the following formulas for determining the distance d and length l of the shunt single stub:
(P7.3.1a)
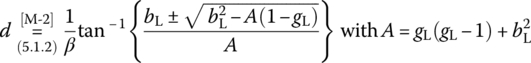 (P7.3.1b)
(P7.3.1b)
- where
(P7.3.2)
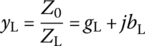 (P7.3.3)
(P7.3.3)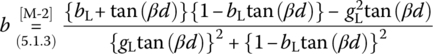
function [ds,ls]=imp_match_1stub_shunt_Misra(Z0,ZL,r,os)% Input: Z0 = Characteristic impedance, ZL = Load impedance% r = a+bi = Propagation constant% os = 'o'/'s' for open/short stub% Output: ds = Distances of the stub from load% ls = Lengths of the stubif nargin<4, os='s'; endif length(Z0)>1, Z01=Z0(2); Z0=Z0(1); else Z01=Z0; enda=real(r); b=imag(r); %lambda=2*pi/b;YL=1/ZL; yL=YL*Z0; gL=real(yL); bL=imag(yL);A=gL*(gL-1)+bL^2;ds=atan((bL+[? ??]*sqrt(bL^2-A*(1-gL)))/A)/b; % Eq. (5.1.2) of [M-2]tbd=tan(b*ds); den=(gL*tbd).^2+(1-bL*tbd).^2;bs=-((bL+tbd).*(1-bL*tbd)-gL^2*tbd)./den; % Eq. (5.1.3,4) of [M-2]ds=mod(ds*b,pi)/b;if lower(os(1))=='s', ls=acot(-bs)/b; % Eq. (5.1.5) of [M-2]else ls=atan(bs)/b; % Eq. (5.1.6) of [M-2]endls=mod(ls*b,pi)/b;- Complete the above MATLAB function ‘
imp_match_1stub_shunt_ Misra()’ so that it uses the above formulas to compute the distances and lengths of two shunt single stubs for impedance matching.
- Use the MATLAB function ‘
imp_match_1stub_shunt()’ (presented in Section 7.3.2.1) and/or the above function ‘imp_match_1 stub_shunt_Misra()’ to determine the distances (from the load) and lengths of single shunt short‐circuited stubs in the unit of wavelength so that they can match a load impedance ZL = 50 − j75[Ω] to the lossless transmission (or feed) line of characteristic impedance Z0 = 100 Ω. - Use ‘Smith 4.1’ to get the solution for the problem dealt with in (b).
- Misra [M-2] presents the following formulas for determining the distance d and length l of the shunt single stub:
- 7.4 Single‐Stub Series Impedance Matching
Consider the single‐stub series impedance matching discussed in Section 7.3.2.2 to find the distance (from the load) and length of series single stub so that they can match a given load impedance ZL to the lossless transmission (or feed) line of characteristic impedance Z0.
- Misra [M-2] presents the following formulas for determining the distance d and length l of the series single stub:
(P7.4.1a)
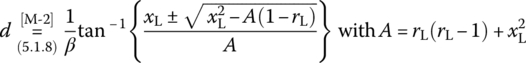 (P7.4.1b)
(P7.4.1b)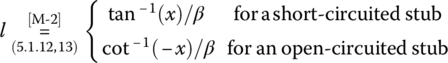
- where
(P7.4.2,3)
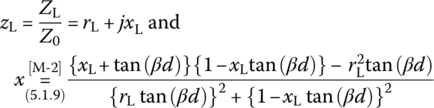
- Complete the following MATLAB function ‘
imp_match_1stub_ series_Misra()’ so that it uses the above formulas to compute the distances and lengths of two series single stubs for impedance matching.
function [ds,ls]=imp_match_1stub_series_Misra(Z0,ZL,r,os)% Input: Z0 = Characteristic impedance of the TL and stub% ZL = Load impedance% r = a+bi = Propagation constant% os = 'o'/'s' for open/short stub% Output: ds = Distance of the stub from the load% ls = Length of the stubif nargin<4, os='s'; enda=real(r); b=imag(r); lambda=2*pi/b;zL=ZL/Z0; rL=real(zL); xL=imag(zL);A=rL*(rL-1)+xL^2;ds=atan((xL+[? ??]*sqrt(xL^2-A*(1-rL)))/A)/b; % Eq. (5.1.8) of [M-1]tbd=tan(b*ds); den=(rL*tbd).^2+(1-xL*tbd).^2;xs=-((xL+tbd).*(1-xL*tbd)-rL^2*tbd)./den; % Eq. (5.1.9) of [M-2]if lower(os(1))=='o', ls=acot(-xs)/b; % Eq. (5.1.13) of [M-2]else ls=atan(xs)/b; % Eq. (5.1.12) of [M-2]endds=mod(ds*b,pi)/b; ls=mod(ls*b,pi)/b;- Use the MATLAB function ‘
imp_match_1stub_series()’ (presented in Section 7.3.2.2) and/or the above function ‘imp_match_1stub_series_Misra()’ to determine the distances (from the load) and lengths of single series short‐circuited stubs in the unit of wavelength so that they can match a load impedance ZL = 100+j80 [Ω] to the lossless transmission (or feed) line of characteristic impedance Z0 = 50 Ω. - Use ‘Smith 4.1’ to get the solution for the problem dealt with in (b).
- Misra [M-2] presents the following formulas for determining the distance d and length l of the series single stub:
- 7.5 Double‐Stub Impedance Matching
Consider the double‐stub impedance matching discussed in Section 7.3.2.3 to find the lengths of stub A (at d0 from load) and stub B (at d from stub A) so that they can match a given load impedance ZL to the lossless transmission (or feed) line of characteristic impedance Z0.
- Misra [M-2] presents the following formulas for determining the distance d and length l of the shunt double stub:
- where
(P7.5.2)
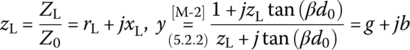 (P7.5.3b)
(P7.5.3b)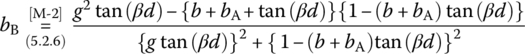
function [lA,lB]=imp_match_2stub_Misra(Z0,ZL,r,d)% Input: Z0 = Characteristic impedance% ZL = Load impedance% r = a+bi = Propagation constant% d = Distance of the stub B from A (load)% where d may be given as [d d0] with d0: Distance of A from load% Output: lA = Length of the stub A at (d0 from) load% lB = Length of the stub B at d from stub Aif numel(d)>1d0=d(2); d=d(1);ZL=Z0*(ZL+Z0*tanh(r*d0))/(Z0+ZL*tanh(r*d0)); % Eq. (7.1.16)endif imag(r)<eps, r=r*i; end % Since a real-valued r must be beta.RL=real(ZL); a=real(r); b=imag(r); lambda=2*pi/b;YL=1/ZL; yL=YL*Z0; gL=real(yL);if gL>csc(b*d)^2 % Eq. (5.2.4) of [M-2]error('Double stub matching is impossible since gL>csc(b*d)^2!');endbd=b*d; tbd=tan(bd);sgd=sqrt(gL*sec(bd)^2-(gL*tbd)^2);bA=cot(bd)*(1-bL*tbd+[? ??]*sgd); % Eq. (P7.5.3a), Eq. (5.2.5) of [M-2]bb1tbd=1-(bL+bA)*tbd;sqgt=(gL*tbd)^2+bb1tbd.^2;bB=(gL^2*tbd-(bL+bA+tbd).*bb1tbd)./sqgt; % Eq. (5.2.6) of [M-2]lA=acot(-bA)/b; lB=acot(-bB)/b; % Eq. (P7.5.1a,b)lA=mod(lA*b,pi)/b; lB=mod(lB*b,pi)/b;- Complete the above MATLAB function ‘
imp_match_2stub_Misra()’ so that it uses the above formulas to compute the lengths of two stubs for impedance matching.
- Use the MATLAB function ‘
imp_match_2stub()’ (presented in Section 7.3.2.3) and/or the above function ‘imp_match_2stub_Misra()’ to determine the lengths of two stub A (at d0 = λ/8 from load) and stub B (at d = λ/8 from stub A) in the unit of wavelength so that they can match a load impedance ZL = 100+j50 [Ω] to the lossless transmission (or feed) line of characteristic impedance Z0 = 50 Ω. - Noting that with the distance d0 = λ/8 of stub A from the load, the virtual load impedance can be regraded as
(P7.5.4)
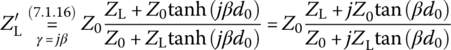
- modify the MATLAB script “elec07e04.m” into “elec07p05.m” so that it returns the solution to this problem.
- Use ‘Smith 4.1’ to get the solution for the problem dealt with in (b) where you may use some transit points (that can be found in (c)) to move the Γ‐point from ΓL to Γ0 = 0 as in Example 7.4.
- 7.6 Quarter‐Wave Transformer (QWT)
Consider the MATLAB function ‘
chebtr()’ presented in [O-1] to design the Chebyshev QWTs (Section 7.3.4.2) satisfying the requirements for attenuation and fractional bandwidth where the attenuation is specified indirectly through reflection coefficient or SWR (standing wave ratio) as(P7.6.1)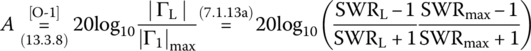
- Here, |Γ1| is the reflection coefficient from the first section of the several section constituting the QWT and |ΓL| is the reflection coefficient from the load. Note that the usage of ‘
chebtr()’ is as follows:
[Y,Az,Bz]=chebtr(Ys,YL,A,fb)- where
(P7.6.2)
- Design a Chebyshev QWT that matches a ZL = 200 Ω‐load to a Z0=50 Ω‐line with SWRmax=1.25 over the frequency band [50, 150] MHz where the center frequency f0 = 100 MHz. You can complete and run the following script “elec07p06a.m”, which uses ‘
chebtr()’ to design such a QWT. Noting that the characteristic admittance vector Y returned as the first output argument of ‘chebtr()’ contains Ys/YL, as the first/last entry, tell the number of sections and characteristic impedances of each section of the designed QWT.
%elec07p06a.mclear, clfZ0=50; ZL=200; % Line characteristic impedance and Load impedanceGL = Z2G(ZL,Z0); SWRmax = 1.25;f1 = 50; f2 = 150; % Band edge frequenciesf0 = (f1+f2)/2; % Operating frequencyfb = (f2-f1)/f0; % Required fractional bandwidthAs = 20*log10(GL*(SWRmax+1)/(SWRmax-1)); % Attenuation of% reflectionless band (relative to unmatched case)[Y,a,b] = chebtr(1/Z0,1/ZL,As,fb); % Chebyshev transformer design% where b/a = Numerator/Denominator polynomials of reflection responseZ = 1./? % Characteristic impedances of each section of designed QWTN=length(Z)-2; % Number of sectionsZr=Z(2:N+1); % Real characteristic impedance vector of designed QWT- To see if the above design Zr satisfies the following QWT conditions:
(P7.6.4)
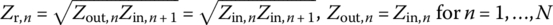
- complete/run the above MATLAB script “elec07p06b.m” and discuss the result (see Figure P7.6.1).
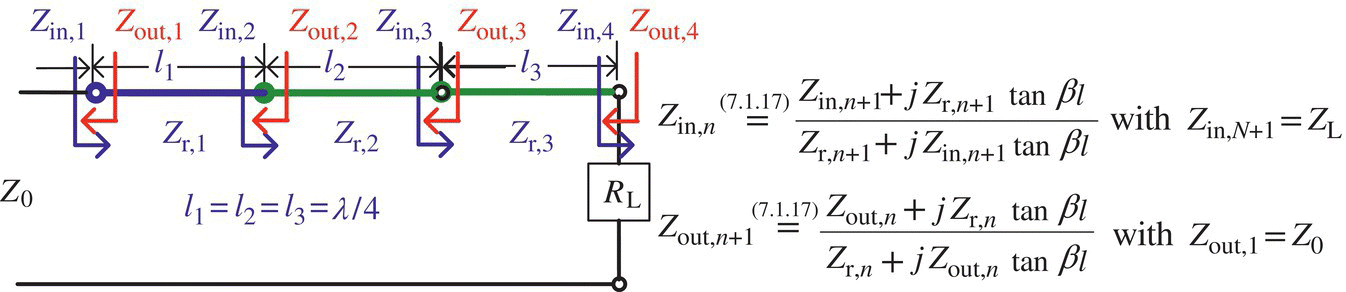
Figure P7.6.1 An N‐section impedance transformer.
%elec07p06b.mZl=@(ZL,Z0,bl)(ZL+j*Z0*tan(bl))./(Z0+j*ZL.*tan(bl))*Z0;Zo(1)=Z0; Zi(N+1)=ZL; bl=pi/2;for n=1:N, Zo(n+1)=Zl(Zo(n),Z?(n),bl); end % Eq. (P7.6.3b)for n=N:-1:1Zi(n)=Zl(Z?(n+1),Zr(n),bl); % Eq. (P7.6.3b)Zr1(n)=sqrt(Zo(n)*Zi(n+1)); % Eq. (7.3.19) at each stageendMismatching=norm([Zi(1)-Z0 Zr-Zr1 Zo-Zi Zo(N+1)-ZL])
Figure P7.6.2 Reflection response and SWR.
- Noting that the fifth input argument of ‘
multi_line()’ (presented in Section 7.3.4) should have the normalized phase constant β = 2π as the first entry, use the MATLAB function to get the reflection response of the QWT designed in (a) and plot it together with SWR (Eq. (7.1.13a)) for the frequency range 0~2fc. To this end, complete and run the following script “elec07p06c.m” to get the graphs as shown in Figure P7.6.2.
%elec07p06c.mf = linspace(0,2*f0,401); % Frequency range [0,200]MHzls = ones(1,N)/4; % Quarter-wave lengthsbb = 2*pi*[1 f/f0]; % Normalized frequency vector% with phase constant beta as its 1st entry[Zin,Gam,bb]=multi_line(Z?,ls,Z0,ZL,bb);SWR = (1+abs(Gam))./(1-abs(Gam)); % SWR by Eq. (7.1.13a)subplot(221), plot(f,abs(Gam)), hold onplot(f([1 end]),max(Gam)*10^(-As/20)*[1 1],'r:')subplot(222), plot(f,SWR, [f1 f2],SWRmax*[1 1],'r:')- To realize the meanings of the second/third output arguments of ‘
chebtr()’ as the denominator/numerator polynomials of the reflection response in z = exp(jπf/f0), use them to compute the reflection response(P7.6.5)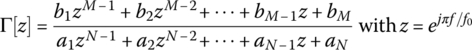
- and see if it conforms with that obtained as the second output argument of ‘
multi_line()’ in (c) by running the following MATLAB script “elec07p06d.m”.
%elec07p06d.mw=pi*f/fc; Gam1=freqz(b,a,w); % Alternative way of computing GamGam1_=polyval(b,exp(j*w))./polyval(a,exp(j*w)); % Eq. (P7.6.5)discrepancy=norm([Gam-Gam1 Gam-Gam1_]) - Here, |Γ1| is the reflection coefficient from the first section of the several section constituting the QWT and |ΓL| is the reflection coefficient from the load. Note that the usage of ‘
- 7.7 Design of LPF Using Stubs [L-1]
With source/load impedances Rs = 50 [Ω]/ZL = 50 [Ω], design a Chebyshev I LPF with passband ripple Rp = 0.5 dB for f ≤ fp (passband edge frequency) = 3 GHz and stopband attenuation As = 40 dB for f ≥ fs (stopband edge frequency) = 6 GHz for fabrication using microstrip lines with shunt stubs only.
Referring to Example 7.5, take the following steps to design such an LPF:
- (Step 0) Determine the order N and cutoff frequency ωc [rad/s] of the LPF to satisfy the given frequency response specifications by running the following MATLAB statements:
>>wp=2*pi*3e9; ws=2*pi*6e9; Rp=0.5; As=40[N,wc]=cheb1ord(wp,ws,Rp,As,'s') - (Step 1) Determine the normalized LPF prototype element values by running
>>Rs=50; % Source (line) characteristic impedancetype='C'; % for the Nth order Chebyshev with Rp[dB]gg=LPF_ladder_coef(N,type,Rp) - (Step 2) Determine the normalized LC values of the prototype LPF by running
>>Rs0=1; pT='T'; wc=1; % for a T-type prototype filter[LCRs,LCRs_,Gs]=LC_ladder(Rs0,gg,pT,wc);LCRs, LCRs_- With the results, fill in the parameter values of the circuit in Figure P7.7.1.
- (Step 3) Convert the L/C values into the impedances of short‐/open‐circuited stubs by running the following statement:
>>[Zs,SPsos]=LC2Z(LCRs,LCRs_); Zs_0=Zs, SPsos_0=SPsos- With the results, fill in the parameter values in Figure P7.7.2(a).
- (Step 4) Noting that even if we are going to convert every stub into parallel (shunt) stubs, we provisionally should convert the two Po's (parallel open‐circuited stubs) Z1 and Z5 (at either ends) into Ss's (series short‐circuited stubs) so that the Ss's Z2 and Z4 can have UEs of Z0 = 1 (needed for conversion), let us use Kuroda identity 1 to convert Z1 and Z5 into Ss's. Thus, we insert UEs between Z1/Z5 and the transmission line (as Figure P7.7.2(b)) and run the following statements:
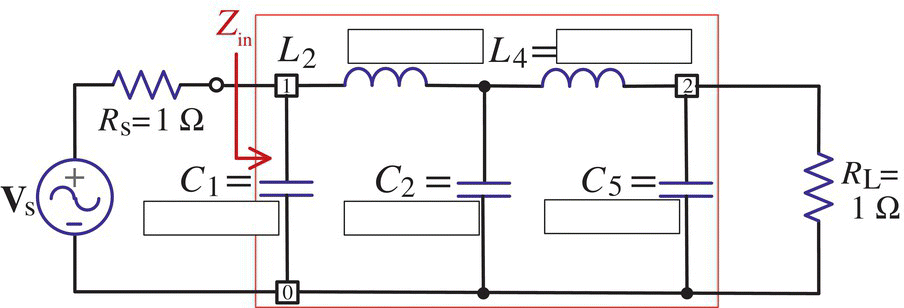
Figure P7.7.1 Normalized prototype LPF of order N = 3.
>> [Z0s(2),Zs(1),SPsos{1}]=Kuroda(Zs(1),SPsos{1});[Z0s(4),Zs(5),SPsos{5}]=Kuroda(Zs(5),SPsos{5});Z0s, Zs, SPsos- With the results, fill in the parameter values in Figure P7.7.2(c).
- (Step 5) Noting that in Figure P7.7.2(c) the two Ss's Z1 and Z5 (at either ends) have no UE needed for conversion (while Z2 and Z4 have UEs), let us insert UEs of Z0=1 between them and TL as shown in Figure P7.7.2(d).
>>Z0s(1)=1; Z0s(5)=1; - (Step 6) Now that every Ss has got its UEs for conversion, let us use Kuroda identity 2 to convert the Ss's Z1, Z2, Z4, and Z5 into Po's by running
>>for m=[1 2 4 5][Z0s(m),Zs(m),SPsos{m}]=Kuroda(Zs(m),SPsos{m},Z0s(m));endZ0s, Zs, SPsos- With the results, fill in the parameter values in Figure P7.7.2(e).
- Alternatively, the process from Step 4 to Step 6 can be performed by using the MATLAB function ‘
S2P_stubs()’ (listed below) as follows:>>Zs=Zs_0; Z0s=zeros(size(Zs)); SPsos=SPsos_0;[Z0sf,Zsf,SPsosf]=S2P_stubs(Z0s(1:2),Zs(1:2),SPsos(1:2));[Z0sb,Zsb,SPsosb]= ...S2P_stubs(Z0s(end:-1:4),Zs(end:-1:4),SPsos(end:-1:4));Z0s_=[Z0sf Z0s(3) Z0sb(end:-1:1)]; Zs_=[Zsf Zs(3)Zsb(end:-1:1)]SPsos_=[SPsosf SPsos(3) SPsosb(end:-1:1)]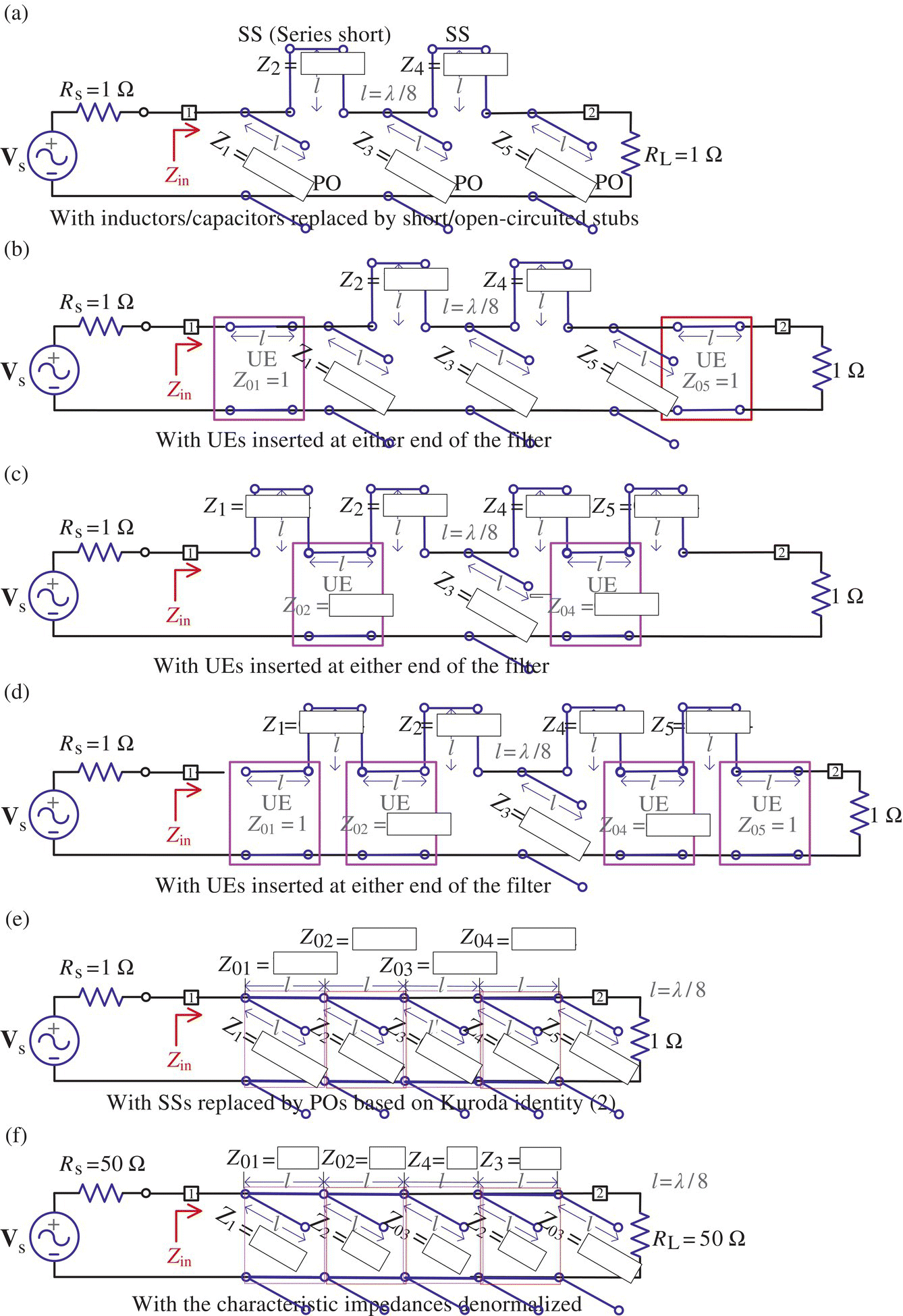
Figure P7.7.2 Microstrip filter design for Problem 7.7.
- (Step 7) Denormalize the normalized characteristic impedances by multiplying them with Rs = 50 Ω:
>>Zs=Zs*Rs, Z0s=Z0s*Rs- With the results, fill in the parameter values in Figure P7.7.2(f).
function [Z0s,Zs,SPsos]=S2P_stubs(Z0s,Zs,SPsos)% To convert all series stubs (SS) into parallel stubs (PS)% Input:% Z0s = Characteristic impedances of UEs with 0 for no UE% Zs = Stub impedances% SPsos = {'Po','Ss', .. } for parallel-open, series-short stubs% Output:% Z0s, Zs, SPsos = Results with all stubs parallel% where any -ve sign of Zs implies that it is an open-circuited stub.N=numel(Zs); nS=N+1;for n=1:N % To find the position of the 1st SSif upper(SPsos{n}(1))=='S', nS=n; break; endendif nS<=N % If any stub is a SSfor n=1:nS-1 % All PSs into SSs before the 1st SS[Z0s(n+1),Zs(n),SPsos{n}]=Kuroda(Zs(n),SPsos{n},Z0s(n));endfor n=1:nS % All the SSs into PSs up to the 1st SS[Z0s(n),Zs(n),SPsos{n}]=Kuroda(Zs(n),SPsos{n},Z0s(n));end[Z0s,Zs,SPsos]=S2P_stubs(Z0s,Zs,SPsos); % Self-calling recursivelyend- (Step 8) Frequency scale the circuit by determining the line/stub lengths as l = λ/8 = vp/fc/8 [m] where vp [m/s] is the phase velocity of signal propagating on the line and fc is the cutoff frequency given as a design specification.
- (Step 9) To plot the frequency responses of the two filters, one (called a lumped‐element filter) consisting of lumped elements L/C (Figure P7.7.1) and the other (called a distributed‐element filter) consisting of microstrip lines/stubs (Figure P7.7.2(f)), complete and run the following MATLAB script “elec07p07b.m” to get the frequency responses as shown in Figure P7.7.3:
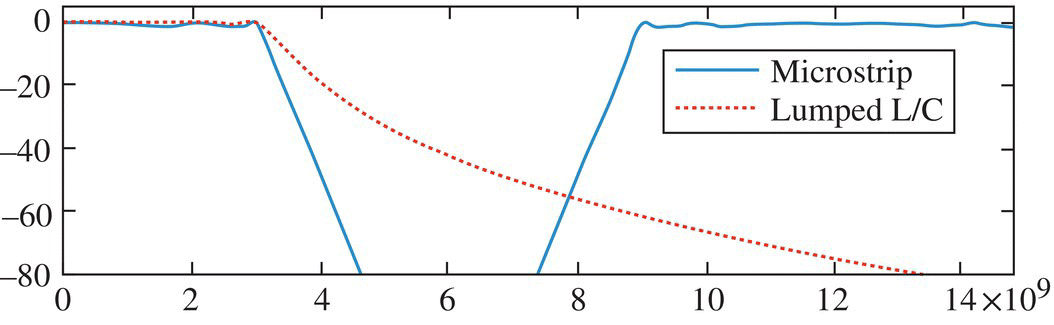
Figure P7.7.3 Frequency responses of the lumped‐element filter and distributed‐element filter.
%elec07p07b.mZ0strip=[Zs(1) Z0?(1) Zs(2) Z0s(?) Zs(3) Z0s(4) ??(4) Z0s(5) Zs(5)];SPsos={SPsos{1} 'Tl' SPsos{2} '??' SPsos{3} 'Tl' SPsos{?} 'Tl' SPsos{5}};l=1/8; fc=3e9; % Stub length and Cutoff frequencyfN=linspace(0,pi/4,1000); % Normalized frequency rangew=fN*2*pi*fc; % Real frequency rangebl=2*pi*w*l/fc; % Range of bl (bl=2*pi*l at f=fc=4e9[Hz])% To get the frequency response and input impedanceZL=Rs; [Gw,Zinw]=GZ_strip(Z0?????,??sos,ZL,bl);Gw=Zinw./(Rs+Zinw).*Gw; % Overall frequency responseGwmag=20*log10(max(abs(Gw),1e-5)); % Frequency response magnitude in dBplot(w,Gwmag-max(Gwmag),'b'), hold on % with the maximum 0dBs=j*w/fc; Gw0=eval(Gs); % Frequency response from the transfer functionGwmag0=20*log10(max(abs(Gw0),1e-5));plot(w,Gwmag0-max(Gwmag0),'r:') % To make the maximum 0dBlegend('Microstrip','Lumped L/C'), axis([w([1 end]) -80 5])- Note that the whole process from Step 1 to Step 7 can be performed by using the MATLAB function ‘
ustrip_LPF()’ (listed below) as follows:>>Rs=50; type='C'; wp=2*pi*3e9; ws=2*pi*6e9; Rp=0.5; As=40[Z0strip,SPsos]=ustrip_LPF(Rs,type,[Rp As],[wp ws],pT)
- (Step 0) Determine the order N and cutoff frequency ωc [rad/s] of the LPF to satisfy the given frequency response specifications by running the following MATLAB statements:
- 7.8 Design of T‐type Impedance Transformers Using the Smith Chart
Consider making T‐type ladders with quality factor Q = 2 for transforming ZL = 20 − j15[Ω] to Zs = 50[Ω] at frequency fc = 2 GHz.
function [Z0strip,SPsos,LCRs,LCRs_]= ...ustrip_LPF(Rs,type,RpAs,wps,pT)% Input:% Rs = Line characteristic impedance% type = 'B'/'C1'/'C2'/'E' for B/Chebyshev I/II/Elliptic filter% RpAs = [Rp As] Passband ripple/Stopband attenuation[dB]% wps = [wp ws] = Passband/Stopband edge frequencies[rad]% pT = 'pi'/'T' for pi-/T-form% This function can be called as ustrip_LPF(Rs,type,Rp,N,pT).% Copyleft: Won Y. Yang, [email protected], CAU for academic use onlyif nargin<5, pT='pi'; end % Pi-form by defaultif numel(wps)<2 % When called as ustrip_LPF(Rs,type,Rp,N,pT)N=wps; Rp=RpAs;elseRp=RpAs(1); As=RpAs(2); wp=wps(1); ws=wps(2);if lower(type(1))=='b', [N,wc]=buttord(wp,ws,Rp,As,'s');elseif lower(type(1))=='c'if numel(type)<2|type(2)=='1', [N,wc]=cheb1ord(wp,ws,Rp,As,'s');else [N,wc]=cheb2ord(wp,ws,Rp,As,'s');endelseif lower(type(1))=='e', [N,wc]=ellipord(wp,ws,Rp,As,'s');else error('What type of filter do you want? (inside ustrip_LPF)');endendgg=LPF_ladder_coef(N,type,Rp);% To find the L & C values of the prototype pi filterRs0=1;[LCRs,LCRs_,Gs]=LC_ladder(Rs0,gg,pT,1);format short e;LCs=LCRs(1:end-1);LCs_=LCRs_(1:end-1);% To convert the L/C values into the characteristic impedance% of short/open-circuited stub[Zs,SPsos]=LC2Z(LCRs,LCRs_);% To convert all SSs (series stubs) into PSs (parallel stubs)M=ceil(N/2);if SPsos{M}(1)~='P', M=M+1; endM1=M+1; Z0s=zeros(1,N);Z0s_f=Z0s(1:M-1); Zs_f=Zs(1:M-1); SPsos_f=SPsos(1:M-1);Z0s_b=Z0s(end:-1:M1); Zs_b=Zs(end:-1:M1); SPsos_b=SPsos(end:-1:M1);[Z0s_f,Zs_f,SPsos_f]=S2P_stubs(Z0s_f,Zs_f,SPsos_f);[Z0s_b,Zs_b,SPsos_b]=S2P_stubs(Z0s_b,Zs_b,SPsos_b);Z0s=[Z0s_f Z0s_b(end:-1:1)];Zs=[Zs_f Zs(M) Zs_b(end:-1:1)];SPsos=[SPsos_f SPsos(M) SPsos_b(end:-1:1)];% Denormalize the normalized characteristic impedances% by multiplying them with Rs.Z0s=Z0s*Rs, Zs=Zs*RsZ0strip=reshape([Zs;[Z0s 0]],1,2*N); Z0strip=Z0strip(1:end-1);SPsos=[SPsos; repmat({'Tl'},1,N)];SPsos=reshape(SPsos,1,2*N); SPsos=SPsos(1:end-1);- Complete and run the following MATLAB script “elec07p08.m” to make such T‐type ladders.
%elec07p08.mZs=50; ZL=20-15i; Q=2; fc=2e9;[LCs1,LCs1_,ff1,Gws1]=imp_matcher_T(??,ZL,-Q,fc);[LCs2,LCs2_,ff2,Gws2]=imp_matcher_T(Zs,??,Q,fc);- Referring to Figure P7.8, note that, with Q ≤ 2, there are four paths along resistance/conductance curves from point ΓL (representing ZL = 20 − j15 [Ω]) to Γs (representing Zs = 50 [Ω]), each via Γ2‐Γ3, Γ4‐Γ3, Γ2‐Γ5, and Γ4‐Γ5 where Γ2 and Γ4 are on the lower and upper Q = 2‐circles, respectively. Use ‘Smith V4.1’ to solve the same design problem as (b).
Figure P7.8 Using ‘Smith 4.1’ to design T‐type impedance matchers in Problem 7.8
- 7.9 Impedance/Admittance from Resistance/Conductance
Complete the following MATLAB function ‘
RG2ZY()’ so that it can return the impedance Z and admittance Y with given resistance R and conductance G. Use it for R5 = 60 Ω and G5 = 0.01 S (Eq. (E7.8.2)) to check if it works properly.function [Z,Y]=RG2ZY(R,G)X=sqrt(R/G-?^2); Z=R+j*X; % Reactance and ImpedanceB=sqrt(?/R-G^2); Y=G+j*B; % Susceptance and Admittance