Abstract

The paper investigates the equilibrium in an economy in which all participants are indifferent to risk. The mechanism of asset and derivative pricing in such economy is identified. It is shown that no economy in equilibrium with stochastic interest rates can be simultaneously risk-neutral and have zero market price of risk. On the other hand, there exist equilibrium economies with risk-averse participants and zero prices of risk.

Introduction

The concept of the risk-neutral economy, that is, an economy in which all participants are indifferent to risk and only care about expected return, is often used in finance as a standard of reference. That is due to the supposition that in such an economy there is no compensation for risk and all assets have the same expected return, which is therefore equal to the risk-free rate.

In general, a complete economy (an economy that allows all derivative contracts) in which there are no opportunities for riskless arbitrage will contain a process, called the market price of risk, for each source of uncertainty it involves. If x is a Wiener process of the risk sources and λ is the vector of the corresponding market prices of risk, and if r is the short riskless rate, then the expected instantaneous rate of return μ on an asset whose exposure to the sources of risk is β satisfies the relationship

1

It is often assumed that in the risk-neutral economy the market prices of risk are all zero and therefore for all assets. Why should there be compensation for risk if all investors are risk-neutral?

This is used in a number of conceptual conjectures. For instance, the general bond pricing formula

2

is claimed in the risk-neutral economy to take the simple form

3

called the expectation hypothesis. Note that when the short rate is deterministic, the expectation hypothesis holds trivially.

It has been noted in Cox, Ingersoll, and Ross (1981) that the returns on different assets in a risk-neutral economy are in general not all the same, and the price of risk is not identically zero. They show that in a production economy of the Cox, Ingersoll, and Ross (1985) type, the expected instantaneous return on any bond (in fact, on any asset) can be written as

4

where

5

and T* is the time of consumption. The second term on the right-hand side of (4), which is the instantaneous covariance of the bond price with the expected return to the consumption date on the money market account, is in general nonzero.

This chapter investigates the relationship between risk neutrality of investors and zero prices of risk in an equilibrium economy. Two questions are posed: First, if all investors are indifferent to risk, are the prices of risk identically zero? Second, are there economies with risk-averse participants and zero price of risk?

The chapter gives an explicit characterization of the risk-neutral economy in equilibrium. It is shown that there is no consumption by the participants until a certain moment, given by the first entry of the state price density process into an absorbing boundary. At that time, the total social wealth is consumed. The pricing of assets in such an economy is explicitly given, and equations for interest rates are provided.

In answer to the two questions, it is shown that no economy in which all participants are indifferent to risk can have zero market price of risk, unless interest rates are deterministic. On the other hand, there exist economies with risk-averse participants and stochastic interest rates in which the price of risk is identically zero.

In the derivative asset pricing theory, the term risk-neutral probabilities is often used to refer to the martingale probability measure under which the expected returns on risky assets are equal to the riskless rate r. It is a misnomer, since the martingale measure does not correspond to the probability measure in a risk-neutral economy.

This chapter draws heavily on the results and methodology of Vasicek (2005, 2013) (Chapters 11 and 12 of this volume).

An Economy in Equilibrium

Consider a continuous time economy with n participants endowed with initial wealth . It is assumed that investors can issue and buy any derivatives of any of the assets and securities in the economy. The investors can lend and borrow among themselves, either at a floating short rate or by issuing and buying term bonds. The resultant market is complete. It is further assumed that there are no transaction costs and no taxes or other forms of redistribution of social wealth. The investment wealth and asset values are measured in terms of a medium of exchange that cannot be stored unless invested in production.

Production in the economy is described by a production process A(t) whose rate of return on investment is

6

where is a Wiener process. The process represents a constant return-to-scale production opportunity. The amount of investment in production is determined endogenously.

The parameters of the production process can themselves be stochastic, reflecting the fact that production technology evolves in an unpredictable manner. It will be assumed that their behavior is driven by a Markov state variable . The dynamics of the state variable, which represents the state of the production technology, is given by

7

where is a Wiener process independent of . The parameters , and ϕ are functions of and t.

In equilibrium, the total wealth must be invested in the production process (which could thus be referred to as the market portfolio). Individual investors may hold financial securities and contracts, such as bonds, futures, and derivatives, in order to optimize their objectives. Because these securities and contracts were issued by other participants in the economy, however, the net borrowing and lending (including lending and borrowing implicit in issuing and buying contingent claims) is zero and the total available wealth is put into production.

An economy cannot be in equilibrium if arbitrage opportunities exist in the sense that the returns on an asset strictly dominate the returns on another asset. A necessary and sufficient condition for absence of arbitrage is that there exist processes , called the market prices of risk for the risk sources , respectively, such that the price P of any asset in the economy satisfies the equation

8

where are the exposures of the asset to the two risk sources. It is assumed that Novikov's condition holds,

9

Let be the state price density process,

10

The price P of any asset satisfies

11

Here and throughout, the symbol E_t denotes expectation conditional on a filtration ℑ_t generated by .

Equilibrium is fully described by specification of the process , which determines the pricing of all assets in the economy, such as bonds and derivative contracts, by means of Eq. (11). Specifically, the price at time t of a default-free bond with unit face value maturing at time s is given by the equation

12

The short rate is given by

13

An asset consisting of reinvestment at the short rate,

14

will be called the money market account.

The Risk-Neutral Economy

In a risk-neutral economy, where each participant is indifferent to risk, each investor maximizes the expected present value of lifetime consumption,

15

where c_k(t) is the rate of consumption at time t and is a time preference function. An investment strategy is fully described by the exposures to the sources of risk . The wealth at time t grows by the increment

16

Let be the value at time t of the expected remaining consumption under an optimal investment and consumption strategy,

17

The process satisfies the Bellman equation for optimality

18

Put

19

with the dynamics of written as

20

Calculating yields the equation

21

The function to be maximized is linear in the decision variables , and . Because , are unrestricted, in order to get a final maximum it must be that

22

If , the rate of consumption will be zero and consequently from (21),

23

When , the rate of consumption will be infinite, with the total consumption equal to the available wealth. Thus, the investor refrains from consuming until the process hits the boundary , at which time the whole wealth is consumed. Eq. (17) takes the form

24

Because the investment strategy is immaterial in virtue of Eqs. (21) and (22), it can be assumed that each participant is fully invested in the market portfolio,

25

From Eqs. (19), (24), and (25),

26

From Eq. (10), the dynamics of the state price density process is

27

Comparing Eqs. (20), (22), (23), and (27), it follows that

28

and therefore

29

where ν_k is a constant. It follows that

30

For equilibrium pricing to exist, the right-hand side of Eq. (30) must be the same for all , which requires that the preference functions all be the same. Equilibrium cannot attain in a risk-neutral economy if the participants have differing time preferences. It will therefore be assumed that . In that case,

31

Note that for all t. Total consumption takes place when for the first time. If is the time point at which the maximum in (31) occurs,

then is equivalent to .

The expectation

32

is a function of X, t only, and therefore the state price density process given by Eq. (31) is likewise a function of the state variable and time, . The market prices of risk are given by

33

34

In order that in a risk-neutral economy, it follows from Eqs. (33) and (34) that either X is deterministic or Y does not depend on X. In either case, is deterministic and so are interest rates. No economy with stochastic interest rates can be simultaneously risk-neutral (i.e., with all participants being indifferent to risk) and have zero market price of risk.

The expected instantaneous returns on different assets in a risk-neutral economy are not in general equal. The same is true for expected returns on the assets over a given finite period. If is the point of absorption of the process into the boundary , however, then

35

The expected return over the term on the money market account is the same as on the market portfolio, and in fact the same on any asset in the economy. Indeed, conditionally on the value of , Eqs. (31) and (11) reduce to

36

and

37

respectively, and therefore

38

for any asset P. Because this is valid conditionally for any value of T*, it is valid unconditionally.

This explains the paradox: In risk-neutral economy in equilibrium, the expected returns are the same on all assets, regardless of their riskiness, over the one period that is relevant to the investors, namely, to the point of consumption. Due to the nonlinearity of compounding, however, this precludes the expected instantaneous returns to be the same, unless they are deterministic. The market price of risk will not be zero.

Two examples of risk-neutral economies follow.

Example 1. Let the time preference function of all participants be

and suppose that

with , and σ constant. Put

and assume for simplicity that . Evaluating the expectation in (32) gives

where

Denote by the time point at which the maximum in Eq. (31) occurs. The state price density process is given by

Total consumption takes place when for the first time, which is equivalent to for the first time. Here is given as

If , consumption takes place immediately at time zero. If , consumption occurs when for the first time, or at the end date T if fails to reach κ.

The risk premia are

Example 2. Suppose that the time preference functions of all participants are concentrated at the point T. In other words, each participant maximizes the expected end-of-period wealth. Then

Bond prices are given by

Specifically,

A contingent claim that pays a random amount at time T is priced as

In an economy with risk-averse participants, this pricing will hold only when the payout is uncorrelated with .

An Economy with Zero Price of Risk

There are equilibrium economies with risk-averse participants in which the price of risk is zero. There is no practical significance of such economies, and they are investigated here solely to demonstrate the disconnection between risk neutrality and zero price of risk.

Suppose each investor maximizes the expected utility of lifetime consumption,

39

where is an isoelastic utility function

40

Here is the reciprocal of the relative risk aversion coefficient, called the risk tolerance.

It is shown in Vasicek (2005) that the optimal consumption rate of the k-th investor is a function of his own preference parameters and initial wealth and of the state price density process only, given as

41

where

42

is a constant determined by the initial wealth. The investor's wealth at time t is

43

(This and other results in Vasicek (2005) are expressed in terms of the so-called numeraire process .)

In equilibrium, the total wealth in the economy

44

is invested in the production process. This produces the equation

45

subject to the terminal condition .

Eq. (45) has a unique solution

46

The state price density is determined as the unique process satisfying Eqs. (45) and (11) (cf. Vasicek (2005)). In the special case that , it is given by

47

where the function is

48

Now assume that the prices of risk in the economy are all identically zero. Then

49

and

50

From Eq. (46), the total wealth is given by

51

where

52

The stochastic part of , given by

53

must by Eq. (45) be equal to and therefore independent of . This is only possible if the values of are all equal. It will therefore be assumed that . The investors may still differ by their time preference functions . Eq. (48) becomes

54

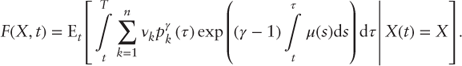
It follows from Eq. (47) that the economy will have zero price of risk if (and only if) the market portfolio satisfies

55

Equation (55) does not seem to have an economic interpretation. It is just a technical condition that needs to be satisfied in order that the prices of risk are zero.

There are two kinds, both rather singular, of economies in equilibrium with risk-averse participants and stochastic interest rates in which the price of risk is identically zero:

1. The market portfolio is instantaneously riskless, , and the investors are myopic with logarithmic utility function of consumption. Each participant is fully invested in the market portfolio (or any combination of derivative contracts equivalent to it).
2. The market portfolio is risky, investors have the same degree of risk tolerance, and the stochastic part of equals . This last condition is sufficient, and necessary, for (55) to hold. This implies . Bond prices, as well as prices of any derivatives, are perfectly instantaneously correlated with the market portfolio.

Example. All investors maximize the expected value of their investments at time T and . The condition (55) becomes

56

where is a constant. For instance, if the dynamics of is as in the Cox, Ingersoll, Ross model of interest rates

where α, are constants and is a deterministic function of time, the expectation in (56) will be finite when . The price of risk will be zero if the volatility of the production process is

where

The production process has the form

with deterministic.

References

1. Cox, J.C., Ingersoll, J.E. Jr. and S.A. Ross. “A Re-examination of Traditional Hypotheses about the Term Structure of Interest Rates.” Journal of Finance, 36 (4), 769–799.
2. Cox, J.C., Ingersoll, J.E. Jr. and S.A. Ross. (1985). “An Intertemporal General Equilibrium Model of Asset Prices.” Econometrica, 53, 363–384.
3. Vasicek, O.A. (2005). “The Economics of Interest Rates.” Journal of Financial Economics, 76, 293–307.
4. Vasicek, O.A. (2013). “General Equilibrium with Heterogeneous Participants and Discrete Consumption Times.” Journal of Financial Economics, 108, 608–614.