Forward and Futures Contracts on Nonstorable Commodities: The Case of Electricity

Most of the literature about modeling commodity spot and futures prices has dealt with storable commodities, such as wheat, gold, and oil. However, the deregulation of energy markets worldwide over the past few years has paved the way to free electricity markets, both for spot and derivatives trading, and made it necessary to focus on electricity's unique features as a commodity.

The most important feature is the nonstorability of power (except for hydroelectricity). It accounts for the spikes observed during periods of extreme weather conditions and/or lack of capacity: for example, in the U.S. Midwest in June 1998; on the U.S. East Coast in July 1999; and in California in much of 2000, followed by severe blackouts in early 2001.

From a financial economics standpoint, the nonstorability makes irrelevant (as argued by Eydeland & Geman, 1998) the notion of convenience yield, which represents the benefits accrued from “holding” the commodity. It also implies the collapse of the spot-forward relationship, as its proof involves cost-of-carry arguments between the current date and the maturity of the forward contract. Besides the nonstorability, electricity has unusual physical attributes that makes the design of well-functioning markets difficult: Rather than following regulatory rules or the rules of supply and demand balancing in each region, electricity obeys physical laws such as Kirchoff laws at each node. When there is congestion at a node, capacity becomes a good in its own right, distinct from electricity. The same fundamental observations would prevail in the case of cable-based telecommunications, wireless telecommunications, and bandwidth.

This chapter has three aims:

1. To examine the specific properties of forward contracts, since they play a central role in the electricity industry, not only in the trading agreements that have existed for decades but also for risk management purposes made necessary by today's highly volatile markets.
2. To analyze separately the behavior of futures contracts. In the general situation of stochastic interest rates that we consider (and without any assumption of independence between the shocks in the economy affecting electricity prices and interest rates), their prices are different from those of the forward contracts. This property was discussed in Cox, Ingersoll, & Ross (1981) and has to be taken into account when the length of the time period of analysis is too long to assume constant interest rates (which is the case, for instance, when investing in a power plant, a pipeline, or another physical asset).
3. To propose a process for the electricity spot price accounting for the spikes (upward jumps followed at some point by downward moves) observed in the power markets.

The first two points are discussed in the framework of diffusion processes, since our goal is to emphasize the specificities of forward and futures contracts in the case of nonstorability, namely the fact that they may not deserve the terminology of derivatives since they are nonredundant with the underlying asset (see Hakansson, 1979). The technical issues reside in the discussion of the martingale property satisfied under different probability measures by futures and forward prices.

Forward, Futures, and Option Pricing in a Diffusion Setting

Let B(t,T) be the price at time t of a bond with unit face value maturing at time T. Assume for simplicity that bond prices are governed by a one-factor model of the term structure of interest rates,

1

where is the short rate, is the market price of bond risk, and is a Wiener process. An asset consisting of reinvestment at the short rate will be called the money market account.

Assume that the spot price of a unit of energy follows a diffusion process with mean , variance , and a correlation with bond prices ρ. The parameters , , and ρ may exhibit mean reversion, seasonality, and other aspects of the empirical spot price behavior. We can write the dynamics of S (under the actual probability measure) as

2

where Y(t) is a Wiener process independent of X(t) and , .

We wish to investigate the pricing of forward and futures contracts and options. Since energy cannot be stored, it is not possible to set up an arbitrage position between the spot price and the derivative. We can, however, apply the standard arbitrage argument to a position consisting of two derivatives, such as two futures contracts of different maturities, or a futures and a forward contracts. We will start with the pricing of the futures contract.

Let be the price at time t of a futures contract with maturity T on the energy unit. In Appendix A, we show that there exists a process , which we can interpret as the market price of risk corresponding to the risk source , such that

3

There then exists an equivalent probability measure under which is a martingale and

4

This equation gives the pricing of the futures contracts.

The martingale property of the futures contracts and Eq. (4) are valid for storable commodities as well. The difference is that for storable commodities, the expected rate of return on the spot commodity under the risk-neutral measure is the risk-free rate, and consequently is a martingale under . (If there is a benefit/cost of storage accruing to the holder of the commodity at a rate y, called the convenience yield, then the martingale property is satisfied by the process .) This is not true if the commodity is not storable. Both the long and the short position in the underlying commodity have, in effect, infinite carrying costs.

Denote by α the expected relative spot price change under . We have

5

Since the spot process could not be involved in the arbitrage argument, we have in general . In other words, the price of risk is in no relationship to the process describing the spot price. It means that the expectation in the formula for pricing of futures contracts will lead to a different value for a nonstorable commodity than it would have if the commodity could be stored. Due to the fact that is not observable, the futures contract pricing can be only applied relative to each other (i.e., giving the price of one contract in terms of the prices of other contracts).

Let us now turn to the pricing of forward contracts. Denote by G(t,T) the price at time t of a forward contract on the energy unit with maturity at T. As shown in Appendix A, an arbitrage argument between the forward contract G(t,T), a futures contract , the bond , and the money market account implies that is a martingale under . It follows that

6

Again, this formula holds for pricing of forward contracts in general. If the commodity is storable, however, the expectation can be evaluated to yield

This could be established directly by the following well-known argument: The forward contract can be exactly duplicated by issuing a bond with the maturity value , buying the commodity with the proceeds today, and storing it until time T. When the commodity is not storable, this argument, and the aforementioned relationship, is not valid. For a discussion of the martingale property satisfied by the storable commodity forward price, see Geman (1989).

Consider now a European option on an energy unit with an expiration date T, and denote its price by . Let the terms of the option specify that

An arbitrage argument applied to the option, a futures contract , a bond , and the money market account implies that is a martingale under , and

7

Examples

Example 1. Suppose α is constant. Then

Since α is not directly observable, this equation provides only a relative pricing of futures contracts,

In this case, the prices of futures contracts of all maturities can be calculated from the spot price and the price of one contract only.

Example 2. Suppose and are functions of t and only. Then , and is the solution of the partial differential equation

subject to . For instance, if log S follows a Gaussian mean-reverting process with the drift and are constant, then

Example 3. Suppose is deterministic (so that interest rates are Gaussian under the risk-neutral measure) and assume that are also deterministic functions of t. Then

Example 4. Let be deterministic as in Example 3, but suppose that with deterministic. Then

and

The relationship of the forward and future prices, which involves observable quantities only, is quite different in Examples 3 and 4.

Under the assumptions of Example 4, an option to buy an energy unit at time T for a fixed price X is valued as

8

where N is the cumulative normal distribution function and

Note that the Black-Scholes (1973) formula for the valuation of calls, resulting from replacing by , does not apply to a nonstorable commodity such as electricity. For the pricing of options on nonstorable commodities, it is not sufficient to know the current spot price; such options can only be priced relative to the forward curve.

Expectations and Risk Premia

Leaving aside the issue of stochastic interest rates, in this section we discuss the relationship between forward (or futures) prices and the realized values of spot prices for the corresponding maturity.

The rational expectations hypothesis, first expressed in the framework of interest rates by economists such as Keynes and Lucas, states that forward prices are unbiased predictors of futures prices, namely that , where E_t denotes the expectation with respect to the true probability measure conditional on the information available at time t.

Other economic theories view these quantities as related but not identical, the differences accounting for risk premia (whose full specification, whether they are assumed to be constant or functions of time t and maturity T, is not straightforward to establish). On the other hand, the arbitrage theory developed in a thorough manner for the past twenty years in the framework of traded financial assets, establishes that futures prices are martingales under the risk-neutral probability measure , or in other words,

Obviously, in the absence of risk premia, and the previous relationship reduces to the rational expectations hypothesis. Given the relatively short period of observations of electricity prices available in the framework of deregulated markets worldwide, we maximize the number of pairs (forward, spot prices) in our analysis by comparing day-ahead prices with realized prices of the following day. In order to avoid the specific problems of California, which would deserve a study by itself, we consider a database of 740 observations at the western hub of PJM (Pennsylvania–New Jersey–Maryland), another vibrant part of the U.S. economy. Figure 29.1 plots the differences between spot prices and day-ahead values and allows us to sketch the following conclusions:

1. The mean is negative.
2. The distribution is skewed to the left.
3. These features become more accentuated when one reduces the analysis to summer periods, times when the consumption of air-conditioning in businesses and households entails a sharp rise in demand, and explains why industrial corporations and wholesale marketers are prepared to pay a risk premium for hedging away the risk of power disruption.
4. Conversely, during the so-called shoulder months of April or October, this property is much less true and the distribution of the spreads becomes symmetric.

These elements tend to support the existence of risk aversion and risk premia in power markets (one expression of these being the development of weather derivatives), hence the probability measures earlier denoted as P and P^* are distinct. When pricing options on futures, the use of a valuation formula written in terms of the forward prices only (as in Eq. (8)) is admissible from an economic standpoint, since all instruments satisfy the martingale property under P^*; hence the representation and calibration of the forward prices process should take place under P^*. The hedging portfolio held by the option seller only involves forward contracts; the underlying and the option are redundant instruments, as in the Black-Scholes world. Not surprisingly, these options represent a liquid market in all deregulated countries.

The remaining issues are of a mathematical nature and related to the consequences for forward prices of the spikes in the electricity price processes as discussed next. (One may arguably view the shocks as toned down when translated into forward prices.)

In the case of daily power options, however, the situation may be described as “bad news on all fronts”: Not only does the option seller need to account for the spikes, fat tails, and stochastic volatility of the spot price process, but also the seller should bear in mind that these spot prices are observed under the true probability measure P while option prices should be computed under P^*. Or equivalently, the risk premium to be received for the risk bought should be incorporated in the option price. The daily power option market became very illiquid after the first major spike in the power markets, which took place in June 1998 in the East Central Area Reliability (ECAR) Coordination Agreement region of the United States, and has remained so since then.

Energy Price Spikes

Energy prices exhibit sudden increases (often due to a heat wave and the corresponding sharp increase in energy consumption) that can be considered discontinuities in the spot price. If these discontinuities were modeled by a jump process, however, it would not take into account the fact that there is typically a discontinuity of a similar magnitude in the other direction (as when the heat wave ends). To address this issue, we propose the following simple model to describe the spot price spikes: A spike of a fixed magnitude occurs at the change from the normal situation to the heat-wave situation, corresponding to the transition from state 0 to state 1 of a Markov process. Such change is followed by a spike of the same magnitude in the opposite direction, occurring as a transition of the Markov process from state 1 to state 0.

Let be a Markov process in continuous time with state space , and denote the transition intensity from state 0 to state 1 by and the transition intensity from state 1 to state 0 by ,

9

For simplicity, assume that Z is independent of X, Y.

Let the spot price of an energy unit be given by

10

where are deterministic functions. Obviously, this description of the spot price process is meaningful only if the commodity cannot be stored, because otherwise selling energy when and buying the money market account guarantees a positive gain on no investment.

Let be the price at time t of a futures contract with maturity T on the energy unit. It is shown in Appendix B that there exist values such that is a Markov process with transition intensities under an equivalent probability measure . The futures price is a martingale under , and consequently

If are deterministic, the expectation can be evaluated to yield

11

where

12

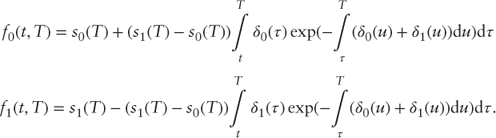
The pricing of the futures contracts can thus be described as follows: The futures price is equal to the expectation of its maturity value, calculated as if the transition intensities of the spot price process were not the actual values , but rather some other values . The intensities cannot be derived from the character of the spot price process, so the pricing is again only relative to the values of other contracts.

The same principle applies to pricing of options. As to the forward contracts, their price is the same as the price of the corresponding futures contracts, due to our assumption that Z is independent of X.

As an example, suppose are constant. Then

We note that here the value of long forward and futures contracts tends to a finite limit

This cannot happen with contracts on storable commodities, where the contract prices increase without limits as the time to maturity increases.

The spot price

We can now propose the following description of the energy spot price process (see Figure 29.2): The spot price has a continuous component and a spike component,

13

The continuous component is subject to the dynamics

14

and the spike component is given by

15

The quantity , which is the magnitude of the spike, is defined as follows: Let be a series of identically distributed positive random variables independent of each other and of . Let be the consecutive transition times of the process from state 0 to state 1,

Then

Typically, the parameters of the continuous component and the transition intensities of the spike component will show an annual periodicity, and .

Futures contracts are priced as

which can be evaluated as

16

where

Here a is a quantity not necessarily equal to . For forward contracts, we have similarly

17

Conclusion

The paper provides a general framework for the pricing of derivatives on nonstorable commodities. It is demonstrated that options and other derivatives can only be valued from the futures or forward curve, rather than from the spot price. A specific process is proposed to describe the observed spot price spikes and time-varying volatility.

Appendix A: Pricing of Futures, Forwards, and Options

Futures

We use the setting described by Eqs. (1), (2), and (3). Building a portfolio comprising futures with maturity , futures with maturity , and bonds with maturity , one obtains through classical argument

Hence

Put

and let be a probability measure whose Radon-Nikodym derivative with respect to P is defined by

The processes

are Wiener processes under . Then

and is a martingale under . Since at the contract maturity , we obtain

This gives the pricing of the futures contracts.

If energy were storable, then (or times a factor accounting for the convenience yield) would also be a martingale under , but this will not be the case for nonstorable commodities.

Forwards

Let be the price at time t of a forward contract on the energy unit at maturity T, with

The wealth gain over an interval resulting from holding the forward contract is

The presence on the left-hand side of reflects the fact that gains or losses on G are locked in the forward position up to its maturity, hence need to be discounted when analyzed at time . Such discounting does not apply to the future contract change in value, since futures are marked to market over time.

Again, standard arguments provide

Hence

so that is a martingale under and

Options

Finally, consider a European option on an energy unit with an expiration date T, and denote its price by . Let the terms of the option specify that

An arbitrage argument applied to the option, a futures contract , a bond , and the money market account implies that

and therefore is a martingale under . The option price is then

Appendix B: Spot Price Spikes

We work in the setting described by Eqs. (9), (10), and (11). Assume that Z is independent of X, Y, and that are adapted to a filtration K_t generated by on an augmented probability space . Write

Then

Consideration of an arbitrage position for Z(t) = 0 yields

The quantity must be positive, because otherwise shorting bonds for each future contract would generate a sure positive gain with no investment.

By the same argument for ,

with positive. On substitution,

The values of are adapted. Let be a probability measure that is the same as before on J, but under which is a Markov process with transition intensities . The measure is equivalent to P, with Radon-Nikodym derivative

Then

Therefore, is a martingale under , and

References

1. Amin, K., and R. Jarrow. (1992). “Pricing Options on Risky Assets in a Stochastic Interest Rate Economy.” Mathematical Finance 22, 217–237, reprinted as Chapter 15 in Vasicek and Beyond, L. Hughston (ed.), London: Risk Publications.
2. Black, F., and M. Scholes. (1973). “On the Pricing of Options and Corporate Liabilities.” Journal of Political Economics, 81, 637–659.
3. Cox, J., J. Ingersoll, and S. Ross. (1981). “The Relation Between Forward Prices and Futures Prices.” Journal of Financial Economics, 9, 321–346.
4. Eydeland, A., and H. Geman. (1998). “Pricing Power Derivatives.” Risk, October, 71–73.
5. Geman, H. (1989). “The Importance of the Forward Neutral Probability Measure in a Stochastic Approach to Interest Rates.” ESSEC working paper.
6. Geman, H., and A. Roncoroni. (2001). “A Class of Marked Point Processes for Modeling Electricity Prices.” ESSEC working paper.
7. Hakansson, N. (1979). “The Fantastic World of Finance: Progress and the Free Lunch.” Journal of Quantitative and Financial Analysis 14 (4), 717–734.