Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

4
Robotic Vehicle Model

In this chapter we extend the graph rigidity‐based formation control framework to multi‐robotic vehicles. As opposed to the simple linear models of Chapters 2 and 3, the agent model here will include the nonlinear kinematics and dynamics of the vehicle. Specifically, we will consider a class of robotic vehicles moving in 2D which includes unicycle robots, marine (surface) vessels, underwater vehicles with constant depth, and aircraft with constant altitude.

In the first part of the chapter we will only account for the nonholonomic kinematics of the vehicles and design a velocity‐level control law based on the main result from Chapter 2. In the second part, we will include the holonomic vehicle dynamics in the control design. Since the resulting dynamic model will be a second‐order nonlinear differential equation, the backstepping methodology will again be utilized to embed the velocity‐level inputs from Chapter 2 in the torque/force‐level control law. Two controllers will be presented in this second part. First, we consider the case where the dynamics are completely known, leading to the design of a fully model‐based formation controller. We then assume the model is subject to parametric uncertainty. In this case, we use adaptive control tools to add parameter adaptation to the control law for the purpose of compensating for the unknown parameters.

The discussions in this chapter are limited to the static formation acquisition problem. Extensions to the other formation problems are left as an exercise for the reader.

4.1 Model Description

Consider a heterogenous system of robotic vehicles moving autonomously on the plane. Figure 4.1 depicts the th vehicle, where the reference frame is fixed to the Earth. The moving reference frame is attached to the th vehicle with the axis aligned with its heading (longitudinal) direction, which is given by angle and measured counterclockwise from the axis. Point denotes the th vehicle's center of mass, which is assumed to coincide with its center of rotation.

We assume the following model for the vehicles 92, 93

(4.1a)

(4.1b)

for , where the first (resp., second) equation describes the vehicle kinematics (resp., dynamics). In (4.1a), is the position and orientation of relative to (a.k.a. the pose of the robot), , is the th robot's translational speed in the direction of , is the th robot's angular speed about the vertical axis passing through , and

(4.2)

In (4.1b), diag, is the th vehicle mass, is the th vehicle moment of inertia about the vertical axis passing through , is the constant damping matrix, and represents the force/torque‐level control input provided by the actuation system.

Image described by caption and surrounding text. — Figure 4.1The th robotic vehicle.

The main challenge in dealing with (4.1) is that the vehicle kinematics 4.1a is nonholonomic¹ since the dimension of the admissible velocity space () is smaller than the dimension of the configuration space (). This is because the vehicle cannot move in the direction of axis (e.g., the wheels of a robotic car cannot slide sideways). In other words, nonholonomic constraints limit the system mobility by constraining the path that the robot can take from an initial pose to a final pose. From a control perspective, it has been shown that nonholonomic systems cannot be stabilized with continuous, static state feedback 95. This is known as Brockett's condition.

4.2 Nonholonomic Kinematics

We will first only consider the kinematic equation 4.1a and design a velocity‐level control law by treating as the control input. As in previous chapters, we will make use of the basic formation acquisition control term formulated in Section 2.1.

4.2.1 Control Design

Since 4.1a is a single‐integrator‐like equation, we will decompose it as follows

(4.3a)

(4.3b)

where are the velocities of point in the and directions, respectively. If we could directly specify these velocities, then (4.3a) is identical to (2.1) and we just set to (2.20). Therefore, the problem becomes to simply solve the algebraic equations

(4.4a)

(4.4b)

for and where are given by the right‐hand side of (2.20). If we multiply the top (resp., bottom) equation by (resp., ) and add them up, we obtain

(4.5)

If we divide (4.4b) by (4.4a), we get

(4.6)

Now, since we cannot directly specify , we let represent the desired value for and set it to the right‐hand side of (4.6).² If is the orientation error, we have that

(4.7)

where

and

Based on (4.7), we can design

(4.8)

to make exponentially stable.

4.2.2 Simulation Results

The simulation of the kinematic control law given by (4.5) and (4.8) consisted of five vehicles forming the regular pentagon in Figure 4.2, where , , , , , , , , and .

The initial pose of each vehicle was set to

The control gains were chosen as and .

The trajectory of the pose of point for each vehicle is shown in Figure 4.3. Notice that the final orientation of each vehicle is 0 rad since becomes zero when the formation is acquired and therefore the right‐hand side of ( 4.6 ) also becomes zero.³ The distance and orientation errors are depicted in Figure 4.4 while the control inputs are given in Figure 4.5.

Two graphs with time on the horizontal axis, ei and θi on the vertical axis, and multiple curves plotted originating from the vertical axis for Distance errors eij(t), (i, j) (top) and orientation errors θi(t), i = 1,..., 5 (bottom). — Figure 4.4Distance errors , (top) and orientation errors , (bottom).

Two graphs with time on the horizontal axis, vi and ωi on the vertical axis, and multiple curves plotted originating from the vertical axis for Control inputs vl(t), i = 1,...5 (top) and ωl(t), i = 1,...5 (bottom). — Figure 4.5Control inputs , (top) and , 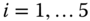(bottom).

4.3 Holonomic Dynamics

Here, we use a trick that bypasses the nonholonomic constraint present in (4.1) and allows us to treat the robot as an Euler–Lagrange system. To this end, we define the “hand” position for the th robot as the point that lies a distance along the axis from point (see point in Figure 4.1). The hand position is then given by

(4.9)

In practice, the hand position could represent a point of interest on the robot such as an end‐effector or a sensor.

The advantage of using (4.9) as the point to be controlled is that its kinematics are holonomic for any . Specifically, from (4.1a), (4.2), and ( 4.9 ), we have that

(4.10)

where

(4.11)

which is invertible for .⁴ The trade‐off for this simplification is that we are no longer controlling the robot per se. Rather, we are controlling point and the robot center of mass could end up anywhere on a circle of radius around .

Taking the time derivative of (4.10) and pre‐multiplying the resulting equation by , we obtain

(4.12)

where (4.1b) and ( 4.10 ) were used. Now, pre‐multiplying (4.12) by , we arrive at the following Euler–Lagrange‐like dynamic model

(4.13)

where

(4.14)

The expressions for the mass matrix and the Coriolis/centripetal matrix are given in Appendix D.

The transformed dynamics (4.13) satisfy the following properties, which can be easily verified from the expressions in Appendix D. These properties will prove useful during the subsequent control design and stability analysis.

4.3.1 Model‐Based Control

In this section, we assume model (4.19) is exactly known for each of the vehicles. We begin by rewriting (4.19) as

(4.19a)

(4.19b)

where represents the hand velocity of the th robotic vehicle relative to . Comparing (4.19) with (3.1), one can see that the double‐integrator model is a simplified version of (4.19).

Due to this similarity, we use a Lyapunov function candidate akin to the one in (3.5). Namely, we introduce the function

(4.20)

where was defined in (2.10), was defined in (3.4)⁵, , and

Note that (4.20) is positive definite with respect to because of Property 4.1.

After taking the time derivative of ( 4.20 ), we obtain

(4.21)

where ( 4.13 ) and (4.16) were used,

and .

The control law that solves the formation acquisition problem is given in the following theorem.

Proof

The proof of part (i) is very similar to the proof of Theorem 3.1 so some details are omitted. Substituting (4.22) into (4.21) leads to

(4.23)

From (4.15) and ( 4.20 ), we have that

(4.24)

for , where

(4.25)

The rest follows as in the proof of Theorem 3.1.

Because we use a transformed model in the control design, it is important to show that all system signals (including “internal” signals) are bounded. Since is exponentially stable, we know , from which we can show using (2.6) and (2.9). From (3.9) and (2.15), we then know . From (3.4), we can state that . From (3.12), we know . Now, since and converge to zero exponentially, so does (see (3.4) and (3.9)), therefore (see Appendix B). From ( 4.22 ), we conclude that . From (4.11), we can see that since all elements of the matrix are trigonometric terms. Therefore, we know from (4.14) that . From ( 4.13 ) and ( 4.15 ), we have that . Since , we know from ( 4.10 ). Then, from (4.1a) and ( 4.2 ), we have that . From (4.1b), it is obvious that . Since converges to zero exponentially, we know from ( 4.10 ) that converges to zero exponentially. This in turn tells us that , and therefore , converge to zero exponentially from (4.1a). As a result, . Finally, from ( 4.9 ), we know that . This concludes the proof of part (ii).□

A comparison of ( 4.22 ) with (3.8) shows that the extra terms in ( 4.22 ) are used to cancel the dynamic terms that appear in ( 4.21 ), i.e., to feedback linearize the system. As a result, the right‐hand sides of (4.23) and (3.10) are identical.

The th control input is given by

(4.26)

where was defined in (3.16). In comparison to (3.15), the control input for the th vehicle is also a function of its own heading angle and rate, which can be measured with onboard sensors. Notice that the controller does not depend on the hand position or the center of mass position .

4.3.2 Adaptive Control

Here we consider the more realistic case where the parameters in (4.18) are subject to uncertainty and therefore their values are unknown to the designer.

First, by making use of Property 4.3, ( 4.21 ) can be rewritten as

(4.27)

where

represents the matrix direct sum (see Appendix A), and . Likewise, the model‐based controller ( 4.22 ) can be expressed as

(4.28)

We now have the constraint that the parameter vector is unknown and cannot be used in the control law. Therefore, the formation controller will include a dynamic estimate of each , whose adaptation law will be part of the control design. To this end, let be the th parameter estimate and define the corresponding parameter estimation error as

(4.29)

To solve the problem, we use the (indirect) adaptive control

(4.30a)

(4.30b)

where was defined in (3.9), , and is constant, diagonal, and positive definite. This is a certainty equivalence‐type control law since is simply replaced by the estimate that comes from the adaptation law (4.30b). The following theorem delineates the stability result we obtain with (4.30).

Proof

Define the Lyapunov function candidate

(4.31)

where was given in ( 4.20 ). Differentiating (4.31) and then substituting (4.30a) yields

(4.32)

where (4.27) was used. Now, after substituting (4.30b) into (4.32), we obtain

(4.33)

By following the arguments originally set forth in the proof of Theorem 2.1, we can state

(4.34)

From ( 4.31 ) and (4.34), we know that . From (2.6) and (2.8), we then know . From (3.9), we know ; thus, from (3.4). From (3.14) and (3.12), we know . Since , we know from ( 4.10 ). From (4.1a) and ( 4.2 ), we have that . From (4.30a) and the fact that appears only through trigonometric functions, we know . Then, since , we have that from ( 4.14 ). From ( 4.13 ) and ( 4.15 ), we know . From (4.1b), we know .

It follows from ( 4.34 ) that for . Since we previously showed that , we can invoke Theorem C.3 to conclude that as for . Therefore, we know from (2.9) that as for . From this point, we can again proceed as in the proof of Theorem 3.1 to claim Iso as for .□

4.3.3 Simulation Results

A five‐vehicle simulation was conducted using the following parameters: kg, kg‐, diag kg/s, 0.004 kg‐/s, and m for . The simulation consisted of applying control law (4.30) to (4.1) using the fact that from ( 4.14 ). The desired formation was the regular convex pentagon described in Section 2.6.1.

The initial position of the th vehicle, , was randomly chosen as a perturbation about while its initial orientation, , was randomly set to a value between 0 and . The initial position of each vehicle's mass center was then obtained from ( 4.9 ). The initial translational and angular speed of each vehicle were set to m/s and rad/s, respectively. The initial conditions for the parameter estimate vector was . The control and adaptation gains were set to , , and .

Figure 4.6 shows the trajectories of the robots’ hand position , forming the desired shape, while Figure 4.7 shows the distance errors , converging to zero. Notice that the vehicle orientations are rather random upon reaching the final position. This is because the controller is based on the hand position, which is a point, rather than on the vehicle position and orientation. The actual control inputs applied to (4.1) are depicted in Figure 4.8. As an example of the behavior of the parameter estimates, the parameter estimates for vehicle 1, , are shown in Figure 4.9. The fourth and fifth components of converge to zero since they are related to and , respectively, which were set to zero in the simulation. The parameter estimates for all the other vehicles also converged to constants as expected.

Graph with time on the horizontal axis, eij on the vertical axis, and multiple curves plotted in different shaded originating from the vertical axis for distance errors eij(t). — Figure 4.7Distance errors , .

4.4 Notes and References

Some work in the literature has accounted for the vehicle kinematics and dynamics during the design of coordination controllers for multi‐robot systems. For nonholonomic models, results can be divided into two categories: the purely kinematic model where the control inputs are at the velocity level and the dynamic model where the inputs are at the actuator level. Examples of work based on the kinematic model are the following. A class of simple control laws for assembling and coordinating the motions of nonholonomic vehicle formations was discussed in 31. In 96, the nonholonomic kinematics was used to design a formation maneuvering controller and experimental results were presented for three‐wheeled mobile robots. Unicycle robot kinematics were used in 97,98 for designing formation maneuvering controllers. Vision‐based control laws for parallel and balanced circular formations using a consensus approach were developed in 99. In 100, a leader–follower‐type solution was presented for the formation maneuvering problem where the inter‐vehicle interactions are modeled by a spanning tree graph. In 101, a sliding mode controller based on a nonholonomic kinematic model was proposed to stabilize the inter‐robot distances in a cyclic polygon formation. In 102, 103, the rendezvous and formation acquisition problems for unicycle kinematic agents were solved using a discontinuous, time‐invariant control law.

For the case of nonholonomic dynamics, the model of a unicycle robot was used in 104 to design a formation control scheme that maintains the prescribed formation while avoiding obstacle and inter‐vehicle collisions. In 105, a flocking and connectivity‐preserving control algorithm was proposed using each robot's state and the heading angles of neighboring robots. In 2, 36, a class of coordination schemes, including aggregation, foraging, formation acquisition, and target interception controllers, were presented for holonomic and nonholonomic dynamics with uncertainty. The work in 106 introduced a receding‐horizon, leader–follower control framework to solve the formation problem with a rapid error convergence rate.

Examples of work based on the holonomic dynamic model are the following. In 77, consensus‐type controller–observers were formulated to allow a team of followers to track a dynamic leader whose motion is known by only a subset of the followers. A synchronization tracking controller was designed in 107 for the cooperative multi‐robot system. A finite‐time consensus tracking controller for leader–follower multi‐robot systems was proposed in 108. In 109, a robust adaptive formation controller was designed under the presence of parameter uncertainties in the system model. Under the assumption of functional uncertainties, 110 constructed a neural network controller that ensures the multi‐robot system is synchronized with the motion of a dynamic target. In 111, a passive decomposition approach was used to decouple the solution of the formation acquisition and formation maneuvering problems. In 112, an adaptive neural network controller was introduced for formations of marine vessels with uncertain dynamics using the dynamic surface control technique. A formation acquisition and flocking‐type controller was designed in 113 for a fleet of ships using the integrator backstepping technique. Other work that employed backstepping as a means of compensating for the robot dynamics during formation control includes 114–116. The formation maneuvering of fully actuated marine vessels was studied in 117 using the passivity‐based group coordination framework. In 118, a target interception scheme was developed using sliding mode control for vehicle dynamics subject to uncertainty and disturbances.