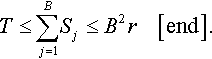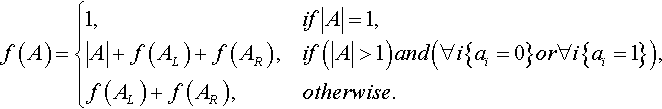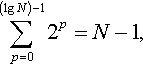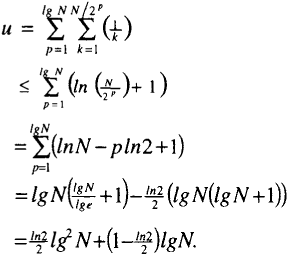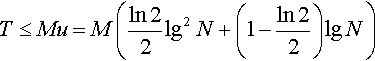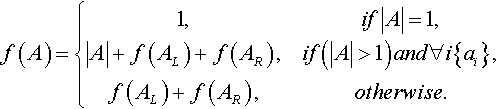Analysis of recombinative algorithms on a non-separable building-block problem
Richard A. Watson [email protected] Dynamical & Evolutionary Machine Organization, Volen Center for Complex Systems, Brandeis University, Waltham, MA, USA
Abstract
Our analysis seeks to exemplify the utility of crossover by studying a nonseparable building-block problem that is as easy as possible under recombination but very hard for any kind of mutation-based algorithm. The interdependent fitness contributions of blocks in this problem produce a search space that has an exponential number of local optima for a mutation-only algorithm. In contrast, the problem has no local optima for a recombinative algorithm - that is, there is always a path of monotonically increasing fitness leading to the global optimum. We give an upper bound on the expected time for a recombinative algorithm to solve this problem by proving the existence of a path to the solution and calculating the time for each step on this path. Ordinarily, such a straightforward approach would be defeated because both the existence of a path, and the time for a step, are dependent on the state of the population when using recombination. However, to calculate an upper bound on the expected time it is sufficient to know certain properties, or invariants, of the population rather than its exact state. Our initial proofs utilise a 'recombinative hill-climber', which applies crossover repeatedly to just two strings, for this purpose. Though our analysis does not transfer directly to a GA with a full population, a solution time based on the assumption that the population has the necessary invariant properties agrees with empirical results.
1 INTRODUCTION
A fitness landscape is a surface defined by a space of candidate solutions, a fitness function acting on these solutions giving the height of the surface at that point, and a neighbourhood metric that determines the proximity of solutions in the space (Jones 1995). We understand certain properties of this landscape to indicate critical features of problem difficulty – for example, a rugged surface, with many local optima, is taken to indicate a difficult problem (Kauffman 1993). Despite the common usage of fitness landscapes in attempting to gain intuition about problems, we are aware that they have their limitations. Jones cautions us that the proximity of points in the space should be determined by the variation operators provided by the algorithm. For example, two points that are distant under mutation may be close under recombination and so these two different neighbourhood metrics produce very different fitness landscapes. From this point of view, properties like ruggedness do not indicate the difficulty of a problem, per se, but rather the difficulty of a problem for some algorithm. The task of a successful algorithm can therefore be seen as the task of re-organizing the space of candidate solutions such that the resulting landscape is favourable: for example, to reorganize the space such that there are fewer local optima. Characterising the different features of a fitness landscape under different operators can assist us in understanding the problem class for which those operators are well suited.
Unfortunately, it is very difficult to imagine exactly what kind of structure a fitness landscape has when it is transformed by recombination, and worse, since the reachable-points from any given point are dependent on the current state of the population, the shape of the landscape must change as search progresses. Although this may limit the intuition we can gain from imagining landscapes, we may nonetheless retain the notion that under a successful variation operator a problem may be 'easy', whereas under another operator, say mutation, the problem may appear difficult.
It can be quite straightforward to calculate an expected time to solution when there are no local optima in a problem – that is, when there is a path of monotonically increasing fitness from any point in the search space to the solution. In this case, the expected time is simply the product of the length of this path and the expected time for each step on the path. This is the approach that we will take in the following analyses. The interesting part will be to prove the existence of such a path under recombination despite the fact that there is no such path for a mutation based algorithm. Ordinarily, such a straightforward approach would be defeated because both the existence of a path, and the time for a step, are dependent on the state of the population when using recombination. However, to calculate an upper bound on the expected time it is sufficient to know certain properties, or invariants, of the population rather than its exact state. For example, Wright and Zhao (1999) provide an analysis of a recombinative algorithm on a separable building-block problem by using the property of the algorithm that prevents alleles from being lost. Under these conditions (that we will detail shortly) there is always some recombination operation that will improve the fitness of the best individual in the population.
Here we extend this idea to a non-separable, hierarchical building-block problem. First, we analyse a 'recombinative hill-climber' that applies crossover repeatedly to just two strings. This simplification provides appropriate invariants that enable us to prove that there is always some choice of crossover points that will improve fitness, and to give an expected time to find such an improvement. Accordingly, we are able to give an analytical time to solution on this problem, and this is far faster than could be expected from a mutation-based hill-climber.
These analyses are possible because of particular regularities in the standard form of the problem; when these regularities are removed the recombinative hill-climber fails. Nevertheless, the principle of an algorithm that follows the recombination landscape is useful to us in less restricted cases. We show that a variant of the problem that is not solvable by the recombinative hill-climber is solvable by a true GA – that is, a GA using a population. Though our analysis does not transfer directly to the true GA, a solution time based on the assumption that the GA is exploiting the recombination landscape agrees with empirical results.
1.1 A TEST PROBLEM APPROPRIATE FOR RECOMBINATION
The building-block hypothesis (Holland 1975, Goldberg 1989) states that the GA will perform well when it is possible to combine low-order schemata of above-average fitness to find higher-order schemata of higher-fitness. The simplest kind of problem for us to imagine where this property of schemata is true is a separable building-block function. That is, a problem where the fitness of a string can be described as the sum of fitness contributions from a number of non-overlapping partitions. When such a problem has tight-linkage, (i.e. when the bits of a partition are adjacent on the genome), then it is quite possible for recombination to combine above average fitness schemata corresponding to these blocks to find higher-order schemata of higher-fitness. Accordingly, much of the GA literature uses building-block problems that are separable. However, the unfortunate characteristic of tight-linkage separable building-block problems is that they can be solved by mutation-based hill-climbers much faster than by GAs (Forrest and Mitchell 1993, and Mitchell et al, 1995). Even when each building-block corresponds to a deceptive trap function, a particular hill-climber, the macromutation hill-climber (MMHC), can out-perform the GA by using the assumption of tight-linkage to cluster mutations on one sub-function at a time (Jones, 1995 pp. 57–58). So we must look to a different kind of problem to exemplify the utility of the GA.
There are at least two ways to break these hill-climbing algorithms that perform so well on separable problems. One is make the problems non-separable, and the other is to remove the assumption that the bits of a block are adjacent on the genome. These two alternatives correspond to unfavourable epistatic linkage and unfavourable genetic linkage, respectively. Genetic linkage refers to the proximity of genes on the genome and their corresponding tendency to travel together during crossover. Epistatic linkage refers to the interdependency of gene contributions (without regard for gene position).1 The trouble with problems that have poor genetic linkage is that, although they defeat all kinds of hill-climber, including the MMHC, they also defeat the GA - when the bits of a block are non-adjacent, crossover cannot combine building-blocks effectively. There has been considerable effort directed at overcoming difficult genetic linkage (e.g. Harik & Goldberg 1996, Kargupta 1997) and the resultant algorithms use recombination operators that are more intelligent than standard crossover. But, our intent in this paper is to address ordinary crossover on building-block problems of tight genetic linkage – the subject of the building-block hypothesis. So, let us return to the other alternative – epistatic linkage. In these problems the fitness of a string cannot be decomposed into the sum of fitness contributions from non-overlapping sub-blocks because the value of one block depends on the setting of bits in another block. The trouble with problems that have epistatic linkage is that its difficult to understand how any algorithm could possibly identify such blocks if their fitnesses are interdependent in this manner. It seems to be a contradiction that a problem can have identifiable sub-parts when these subparts are strongly and non-linearly dependent on one another.
This is likely the reason why issues of epistatic linkage have largely been overshadowed in the GA literature by problems of difficult genetic linkage.2 However, previous work (Watson et al 1998, Watson & Pollack 1999a) identified the class of hierarchically decomposable problems which show that it is possible to define a problem with strong epistatic linkage, (i.e. where the building-blocks are not separable), and yet the blocks can still be discovered and recombined. The canonical example of this problem class, which we call Hierarchical-if-and-only-if (H-IFF), defeats the mutation-based hill-climbing algorithms that solve separable problems. But the GA is able to solve this problem with ordinary two-point crossover. Since this problem is designed to be hard in mutation space but easy in recombination space it provides an appropriate problem for our analyses.
A non-separable building-block problem such as H-IFF is not amenable to analytic approaches usually adopted in the literature. Firstly, it is not possible to apply any analysis that assumes that the population as a whole converges incrementally on particular hyperplanes. In H-IFF the operation of recombination may be defeated if the population is allowed to converge at even one locus. Secondly, most analyses assume separable problems, and, surprisingly often, focus on the extreme case where every bit is separable – the max-ones problem. However, Wright and Zhao (1999) provide an approach to analysis that, although directed at separable building-block problems, can be adapted for our purposes. Their approach is to prove that there is always a way to improve fitness, and then to give a solution time based on the product of the length of the path to the solution, and the time for each step on the path. Here we extend this work to use the same approach for a non-separable problem.
The remainder of this paper is organized as follows: Section 2 describes the analysis of Wright & Zhao. We provide a variation of their model that will be easy to adapt to our needs, and describe the Gene Invariant GA (GIGA) on which both their and our analyses are based. Section 3 describes the problem, H-IFF, that we will analyse, and discusses some of its properties. Section 4.1 proves several theorems for the expected time to find a global optimum in H-IFF using a 'recombinative hill-climber' based on GIGA with a population of two. Our analyses are possible because of particular symmetries in the problem that match properties of GIGA, but the principle behind the operation of recombination is more general. In Section 4.2, we then discuss a variant of H-IFF that is not solvable by the recombinative hill-climber but is solvable by a GA using a real population. Our proofs for solution time cannot be transferred to the population case directly, but we can give an estimate of solution time based on assumptions about the state of the population. These assumptions are somewhat heavy-handed but experimental results in Section 5 support our analytic results, and suggest that the GA is using the recombinative landscape effectively. Section 6 concludes.
2 ANALYSIS ON SEPARABLE PROBLEMS
The analysis provided by Wright & Zhao (1999), and the analyses that follow, feature the Gene Invariant GA (GIGA) (Culberson 1992). The variant of GIGA that best suits our purposes is described in Figure 1.

There are several features to note about this algorithm. Competition is restricted to parents versus their offspring. The two offspring are created from the parents using the same crossover point(s) and so each gene donated by the parents will be acquired by exactly one of the offspring. Given this and the fact that either both offspring are retained or both parents are retained (and there is no mutation) it follows that alleles are never lost from the population – hence, 'Gene Invariant' GA. Finally, note that the algorithm is elitist – the fittest member of the population cannot be replaced by an inferior individual.
Wright & Zhao add several other assumptions to this model: the problem is separable; a set of crossover masks is used that restrict crossover to operations that move exactly one block from one parent to the other; finally, the population is systematically initialised such that every possible bit combination within each block is present. This initialisation gives a population size of ck, where c is the size of the alphabet and k is the number of bits in a block.
These simplifying assumptions enable a useful property to follow: given the gene invariance property of the algorithm and that crossover points are not permitted to move partial blocks, it is guaranteed that building-blocks are never lost from the population; since all possible candidates for a block are present in the initial population and they can never be lost, there will always be some individual in the population that has any block that should be required. Thus, if the best individual in the population is not yet optimal then it must have some sub- optimal block, and this block can be obtained from some member of the population using some crossover mask. This is the invariant property of the population that is required for the analysis. Although the exact structure of the population is not known, this property ensures that there is always some way to improve fitness using recombination.
To calculate an upper bound on the expected time, T, required for the population to find an individual that has reached the global optimum3 Wright & Zhao focus attention on the fittest individual in the population. Their version of the algorithm asserts that one of the parents is the fittest individual (and the other parent is selected at random). The possible states that the algorithm may pass through in the course of search, i.e. the possible populations, are then categorized into equivalence sets based on the fitness of the fittest individual. T is then given by the maximum possible number of fitness increases of this fittest individual, and the time expected for each increase. This yields T = Br(D/d), where B is the number of blocks in the problem (equals the number of crossover masks), r is the size of the population, D is the difference in fitness between the global optimum and the worst possible string, and d is the difference in fitness between the global optimum and the next best string (i.e. the minimum fitness increase for finding a correct block).
In Theorem 1 below we modify the proof provided by Wright & Zhao and use the same assumptions about the problem, crossover masks, and initialisation. However, Wright & Zhao categorize the state of the algorithm using the fitness of the fittest individual in the population and always use this individual as one of the parents. But, we will categorize the state of the algorithm using the number of fully optimised blocks in a particular individual, which we will always use as one of the parents. But, this individual may not be the fittest individual in the population. Indeed, although the fittest individual possible (the global optimum) must have all blocks fully optimised, the fittest individual in the population at a given time does not necessarily have any blocks fully optimised.
In order to transform the theorem to work on the number of optimised blocks we need to be sure that we never reduce the number of optimised blocks when we accept an offspring. We cannot directly measure the number of fully optimised blocks in an individual; neither can we infer the number of fully optimised blocks from a fitness measure. However, we can use the following observation: a fitness increase created by changing one block in an individual cannot reduce the number of fully optimised blocks in that individual. Figure 2 describes a modified algorithm that ensures this condition is applied.

This algorithm is almost the same as the algorithm in Figure 1, but the replacement is more specific about which offspring is compared to which parent. Note that the algorithm only selects one new parent in each iteration, and only evaluates one of the new offspring. This means that maybe the second offspring, c2, was fitter than the one evaluated – and maybe we missed an opportunity to increase fitness. But for our purposes, it is more important that we know that p1 does not decrease in the number of optimised blocks. Although, the algorithm in Figure 2 explicitly makes reference to the fact that the partitions of blocks are known, and that the crossover masks only swap one block at a time, we are not adding any new assumptions to those used by Wright and Zhao. Importantly, note that the modified algorithm maintains the gene invariant property, and the property that building-blocks are never lost from the population.
The intuition behind this analysis is now very simple. T is given by the product of the number of blocks to be found, and the time to find a block in another individual and move it in by crossover. The number of blocks is B, and getting a block into the best individual requires finding the right crossover mask (of which there are B), and picking the right donor individual (of which there are r) – hence B2r, or B2(ck).
This expected time has the desirable property that it is not dependent on any measurement of fitness values in the problem. And the resultant upper bound for T is lower than that which Wright & Zhao provide, at least whenever B < (D/d). Both analytic times assume that each crossover mask corresponds to exactly one block. However, Wright and Zhao's analysis could be modified to a more general set of masks, giving T ≤ Mr(D/d), where M is the number of crossover masks used. This set of masks may include masks that match with more than one block so long as they only match with whole blocks, and it must include the set of masks that correspond to the single fitness blocks, as before. In any case, an approach based on counting optimised blocks, rather than fitness improvements, is better suited to our needs in the following sections.
So we have an upper bound on the expected time to solution for a recombinative algorithm on a separable building-block problem. However, we have to ask whether the simplified problems and algorithms involved in these analyses have captured the interesting properties of a GA. We have permitted modifications to the algorithm that do not violate the assumptions made about the problem – but we notice that we are getting gradually closer to something much simpler than a GA. In fact, notice that using only the same assumptions about a problem as those used above (i.e. that the partitions of building-blocks are known), a simple systematic hill-climbing technique would suffice. That is, in a separable problem with known partitions, each subset of interdependent parameters may be searched exhaustively – i.e. each block may be processed systematically by testing every possible bit combination within that block and selecting the highest fitness configuration. Whilst one block is being processed, we hold the setting of bits in other blocks constant to some arbitrary configuration. The particular configuration of bits used in other blocks does not matter since we know that the blocks are separable. Since systematic search within a block requires testing ck bit configurations, and there are B blocks to be processed, this simple systematic search takes only T ≤ Bck.
Further, for their analysis using GIGA, Wright & Zhao suggest that if the partitioning of blocks is not known then their analytic time can be multiplied by the number of possible partitionings. Since this can be applied to our simple systematic hill-climber too, by this analysis, the simple method is still superior even if the partitioning is not known. We make this observation not to criticize the approach of Wright and Zhao, rather we present it as an illustration that separable problems simply do not justify the use of a population-based recombinative technique. Nonetheless, the above version of Wright & Zhao's analysis provides a good starting point for an analysis of GIGA on H-IFF which is not separable and, we shall argue, does require a recombinative algorithm.
3 HIERARCHICAL-IF-AND-ONLY-IF
In previous work we provided a test problem with sub-blocks that are strongly and non-linearly dependent on one another yet the problem is GA-friendly (Watson et al 1998, Watson & Pollack 1999a). H-IFF is a hierarchically decomposable building-block problem where the blocks are non-separable in a sense which is a little stronger than usual. We define a non-separable building-block problem as one where the optimal setting of bits in one block is dependent on the setting of bits in some other block (or blocks). In this case, we may also say that the blocks are interdependent.
This definition excludes some building-block problems in the literature that are non-separable in a degenerate sense. For example, the second version of the Royal Road problem, RR2, has non-linear interactions between blocks such that the fitness of certain combinations of blocks is not equal to the sum of their independent fitness contributions. However, the 'bonus' fitness contributions never contradict the setting of blocks that are rewarded at the individual block level, and this kind of problem is still solvable by simple mutation-based hill-climbing algorithms.
In H-IFF the interdependency of blocks is implemented in the following manner. At any given level in the hierarchical structure there are two equally valuable schemata for each block. These competing schemata within each block are maximally distinct – specifically, all-ones and all-zeros. From the perspective of this level, it does not matter which solution is found – the blocks are, as far as this level goes, separable. However, higher-order schemata, from the next level up in the hierarchy, are then used to reward particular configurations of schemata from the previous level. For a given block, which of the two schemata should be used depends on which has been used in a neighbouring block – if the neighbouring block is based on ones then so should the block in question, if zeros then zeros. This compatibility of blocks is rewarded by fitness contributions from the next level of the hierarchical structure. Each correct pair of blocks creates a new single block for the next level in the hierarchy. This means that the blocks at the original level were not, in fact, separable, and it creates an interdependency between blocks which is strongly non-linear, but it is highly structured.
We define the fitness of a string using H-IFF with the recursive function given below, Equation 1, (Watson & Pollack 1999a). This function interprets a string as a binary tree and recursively decomposes the string into left and fight halves. Each resultant sub-string constitutes a building-block and confers a fitness contribution equal to its size if all the bits in the block have the same value - either all ones or all zeros. The fitness of the whole string is the sum of these fitness contributions for all blocks at all levels. Figure 3 evaluates an example string using H-IFF.

where A is a block of bits, {a1,a2,… an}, |A| is the size of the block = n, ai is the ith element of A, and AL and AR are the left and right halves of A (i.e. AL = {a1,…an/2}, AR = {an/2,…an}). The length of the string evaluated, must equal 2p where p is an integer (the number of hierarchical levels).
Some features of this apparently simple function should be highlighted. Each block, either ones or zeros, represents a schema that contains one of the two global optima at all-ones or all-zeros. Local optima in H-IFF occur when incompatible building-blocks are brought together. For example, consider “11110000”; when viewed as two blocks from the previous level (i.e. “1111…” and “…0000”) both blocks are good - but when these incompatible blocks are put together they create a sub-optimal string that is maximally distant from the next best strings i.e. “11111111” and “00000000”. However, although local optima and global optima are distant in Hamming space, they may be close in recombination space (Jones 1995); for example, consider a population containing both “11110000” and “00001111” individuals. Thus H-IFF exemplifies a class of problems for which recombinative algorithms are well suited. Watson et al (1998), showed that H-IFF is easy for a GA to solve given that diversity in the population is maintained and genetic linkage is tight. But, since the local optima in H- IFF are numerous and evenly distributed, H-IFF is very hard for any kind of mutation-based hill-climber.
The first proviso for success of the GA, appropriate population diversity, is discussed in (Watson & Pollack 1999a), and superior alternative methods have since been used in (Watson & Pollack 2000a), and (Watson & Pollack 2000b), as will be employed later in this paper. Algorithms to address the second proviso, poor linkage, are addressed in (Watson & Pollack 1999b) and (Watson & Pollack 2000a). The latter work shows that a new form of recombinative algorithm, the “Symbiogenic Evolutionary Adaptation Model” (SEAM), can solve the shuffled H-IFF problem, which has the same epistatic linkage structure as H-IFF but the position of bits is randomly re-ordered giving it difficult genetic linkage also. However, we will not address the poor linkage problem or this new algorithm in this paper. Our focus here is to demonstrate the utility of standard crossover on a building-block problem with tight genetic linkage, as described by the Building-Block Hypothesis.
Tight linkage permits the crossover masks provided by two-point crossover to include a mask for every building-block in H-IFF. And later we will show that one-point is similarly appropriate for H-IFF. The success of the algorithms we analyse depends on this, and the match of the building-blocks to the crossover operators certainly gives crossover an advantage over mutation. Indeed, this is the intent behind the design of the problem. Nonetheless, a successful algorithm must still resolve the strong epistatic linkage in H-IFF. The fact that removing problems of genetic linkage does not make H-IFF easy is evidenced by the fact that non-population based hill-climbers based on the assumption of tight linkage, i.e. macromutation hill climbing, MMHC, cannot solve H-IFF (Watson et al 1998). (Note that MMHC can solve the Royal Road problems, or tight-linkage concatenated trap functions often used in GA testing (Goldberg 1989), much faster than the GA (Jones 1995)).
Variations and more general forms of H-IFF that allow different alphabets (instead of binary), different numbers of sub-blocks per block (instead of pairs), unequal fitness contributions of blocks, and the construction of other hierarchically-consistent building-block functions, are defined in (Watson & Pollack 1999a). For the purposes of this paper, the canonical form given above, and one new variant described later, will be sufficient for illustration.
3.1 DIMENSIONAL REDUCTION
How is it that the GA is able to solve H-IFF easily despite the strong interdependency of blocks? From a bottom-up point of view, we can see H-IFF as defining a hierarchy of building-blocks which may be assembled together in pairs, doubling in size and reward at each level. Accordingly, an algorithm that exploits this structure will be seen to progress from searching combinations of bits at the bottom level, to searching combinations of schemata of successively higher order, at all subsequent levels. At each transition in levels, the dimensionality of the problem is reduced. For example, at the first level in a H-IFF of just 4 bits there are two size two blocks to be processed. Each block has four possible combinations of bits two of which are solutions. At the next level there is one size-four block to be processed, but rather than searching all 16 combinations of bits we need only search the four combinations of “00” and “11” solutions from the previous level. This dimensional reduction enables a recombinative algorithm to take advantage of the problem structure.
Notice that this view is in contrast to the discovery of blocks in a separable problem. In a separable problem the blocks at the first level are discovered unambiguously – there is only one best solution to each block – thus there is no need to search combinations of blocks at the next level (if there is a next level). Similarly, the kind of recombination that is required to put separable blocks together is degenerate – consider the number of block combinations to be searched given by CB, where C is the number of solutions to each block, and B is the number of blocks. In a separable problem C = 1. This is why a hill-climber is able to solve separable problems – there is no need to maintain competing sub-solutions because there are no interdependencies between blocks, and thus the sub-problems can be processed sequentially. In contrast, the structure of H-IFF requires that competing sub-solutions are maintained by the population for at least as long as is required to resolve their interdependencies at the next level in the hierarchy. Section 4 will formalize these intuitive concepts.
3.2 THE H-IFF LANDSCAPE FOR MUTATION HILL-CLIMBERS
Using the notion of a path to solution and the expected time for steps on this path, we may reasonably say that an algorithm is not reliably successful on a problem if there is no guaranteed path to solution, if the path may be exponentially long, or if any step on the path takes exponential time. For a single-bit mutation hill-climber there is no guaranteed path on H-IFF. H-IFF has 2N/2 local optima under single-bit mutation (where N is the size of the problem in bits), only two of which are globally optimal. More generally, a k-bit mutation hill- climber will be faced with 2(N/h) local optima, where h is the smallest integer power of 2 which is greater than k, i.e. h = 2P > k.5 A random mutation hill climber (RMHC) (Forrest and Mitchell 1993) mutates every bit with a given probability Pmut. In principle no problem can have local optima under this operator since the probability of moving from any point to any other point is non-zero. However, consider the case where the current string is N/2 zeros followed by N/2 ones. The next best string is the global optima at all ones or all zeros. To achieve this jump, mutation must flip N/2 bits whilst keeping N/2 undisrupted. The best mutation rate to achieve this is Pmut = 0.5 and this gives an expected time for the step which is 2N – and search is equivalent to random guessing. A macro-mutation hill-climber, MMHC (Jones 1995), has the best chance of success. MMHC chooses two points and randomises the loci between them, thus concentrating mutations on a particular sub-string whilst leaving the remainder untouched. But still, to escape from the next-best optima it must choose the fight points which has probability 1/N(N-1) (this allows macro-mutations both 'inside' and 'outside' the chosen points), and assign all ones (or all zeros) to N/2 bits – this occurs in expected time O(N22(N/2)). Thus we see that by these criteria, all these mutation-based hill-climbers either have no guaranteed path to the optimum, or cannot be guaranteed to take a step on the path in time less than exponential in N.
4 ANALYSES ON H-IFF
The approach of Wright and Zhao is quite intuitive: their algorithm and assumptions guarantee that there is always some choice of parents for which some crossover operation can produce an offspring that is the next step in a progression of individuals which increase in fitness. In other words, their approach is to prove that separable building-block problems have no local optima using their algorithm. We follow the same approach but for non-separable building-block problems, and whereas the proof of Wright and Zhao is based on the fitness of an individual, our approach, as used in Theorem 1, is based on the number of blocks that are fully optimised in an individual.
This condition is central to our approach in this paper. It refers to the ability of an algorithm to utilize the building-block structure of a problem. Or alternatively, to an invariant property of a population that enables an algorithm to utilize the building-block structure. Any algorithm that satisfies Condition 1 and follows such a progression will take time T ≤ BS, where B is the number of blocks to be found in a globally optimal string (equals the maximum number of steps in the progression), and S is the expected time for each step in the progression. For a recombinative algorithm where Condition 1 holds, S ≤ PM, where P is the number of different ways of choosing parents, and M is the number of crossover masks, thus
Equation 2 will hold for any problem that can be described in terms of blocks in some way such that Condition 1 holds. Proving that Condition 1 holds (and that an algorithm follows this progression) will be more or less difficult depending on the assumptions made about the algorithm and the problem. In the separable problem addressed in Theorem 1, Condition 1 holds because all possible configurations for each block are given by initialisation and cannot be lost by the variation operators that the algorithm uses. In Theorem 1, M = B, and P = r, the size of the population. We cannot expect to prove Condition 1 for a standard recombinative algorithm on a general non-separable problem. However, H-IFF is specifically designed to be easy for a recombinative algorithm and, GIGA is ideally suited for adaptation to our purposes.
4.1 A RECOMBINATIVE HILL-CLIMBER
For Theorems 2 and 3 we will reduce the GIGA to a form of hill-climber – by which we mean that we will not use a population to speak of – just two strings. However, this will be a recombinative hill-climber not a mutation-based hill-climber, Figure 4.

Hoehn and Reeves (1996) call recombination like that above “complementary crossover”. Alternatively, one might call it a macro-mutation hill-climber (MMHC) from (Jones 95) that uses bit-flip mutation (instead of assignment of a new random value). Arguably, this is a degenerate form of recombination. Hoehn and Reeves point out that a second parent is redundant. And we concede that the choice of complementary parents is ideally suited to the complementary schemata rewarded in H-IFF. Nonetheless, we maintain that it is more informative to regard the above algorithm as recombining two strings (that happen to be complementary) rather than bit-flipping. Hoehn and Reeves agree that there is a close relation between this operator and crossover, and suggest that the fitness landscape under this operator “reasonably approximates the crossover landscape”. The purpose of using this algorithm here is to illustrate the concept of the crossover landscape as it is found in H-IFF, and to provide a basis for understanding how a true GA might operate on this class of problems by avoiding the local optima inherent in the mutation landscape.
The following theorems do not assume that the algorithm is provided with a set of crossover masks corresponding to blocks in the problem. Ordinary crossover may be used with no restriction on where crossover points may fall. Theorem 2 is based on two-point crossover, Theorem 3 is based on one-point crossover - in the latter case it is a little more difficult to show that Condition 1 holds. Note that these analyses are not restricted to just the one problem instance defined in Equation 1. H-IFF has regular block sizes within a level, regular fitness contributions for blocks within a level, exactly two sub-blocks per block, and global optima that happen to be all-ones and all-zeros. The analyses hold for the class of problems with any of these particulars relaxed, but for these analyses, the global optima must be complementary, and the fitness contribution of competing schemata in the same block partition must be the same. We will discuss in Section 4.2 an extension to the class where building-blocks are not necessarily complementary.
Figure 5 illustrates the reasoning for Condition 1 under one point crossover.

Thus far we have proved that Condition 1 holds on H-IFF for the algorithm in Figure 4 using both 1-point and 2-point crossover. This shows that although a mutation hill-climber finds a number of local optima that is exponential in N, H-IFF has no local optima at all under recombination – there is always some way to increase the number of correct blocks, as Condition 1 states. In this sense, H-IFF exemplifies the transformation of a fitness landscape under different operators from a problem that is very hard under mutation into a problem that is as easy as it could be under crossover. Having shown that there is always a path to an optimum, we now focus on improving our estimate of the time to traverse this path.
We may improve on the upper bounds given in theorems 2 and 3 by returning to our original reasoning, T ≤ BS, where B is the number of blocks to be found (i.e. steps on the path to the optimum) and S is the expected time to find a block (i.e. time to take a step). In the above theorems we prove Condition 1 to assert that there is at least one crossover operation that will find a block given some choice of parents. So we have used S ≤ PM,and accordingly, T ≤ BPM. But it should be clear that for this algorithm on H-IFF there will be many opportunities to increase the number of correct blocks. For example, at the beginning of search there are many size-two blocks to be found and many possible crossovers that may find one.
So, we can use an estimate of time to progress along the path to the optimum that takes account of the fact that the expected time for a step changes with each step, as the number of possible ways to find a block changes. The time to find one of q available blocks is PM/q, thus:
where B is the maximum number of steps in the path to the optimum, P is the number of choices of parents, M is the number of possible crossovers, and qb is the number of ways that an additional block can be swapped-in at the bth step.
Thus, we may write T ≤ PMu, where u is the sum of 1/q for all steps in the path to the optimum. Theorem 4 uses an upper bound on u to give an improved time to solution on H- IFF.
4.2 FROM A RECOMBINATIVE HILL-CLIMBER TO A RECOMBINATIVE POPULATION
Theorems 2 through 4 use the recombinative hill-climber of Figure 4, and in fact, demonstrate that a population greater than this degenerate case of two is not strictly necessary to solve the canonical form of H-IFF. However, this is only the case because of biases in the algorithm that match particular properties of H-IFF. Specifically, GIGA is biased toward finding complementary individuals (a bias which becomes 'the rule' when the population is of size 2), and H-IFF has competing schemata that are exactly complementary. It is quite easy to break this non-population based version of GIGA by making the global optima in H-IFF non-complementary. We can do this by choosing two random strings as the global optima and rewarding left and right sub-strings recursively. Alternatively, and without loss of generality, we can keep one of the optima at all ones and randomise the other. Either way, the bits in the two global optima will agree in some loci and be complementary in others. This prevents the algorithm given in Figure 4 from succeeding since the complement of a good block is no longer (necessarily) a good block. Equation 4 defines a variant of H-IFF based on this idea, that we will refer to as H-IFF2. F(A) runs through the string twice using f and sums results; before the first pass the string is XORed with one global optimum, and before the second it is XORed with the second global optimum, f(A) now simply checks for blocks of all zeros. The fitness of a string, A, under H-IFF2 is given by:
![]()
where A, AL, and AR are as per Equation 1, and p![]() q is the bit-wise exclusive OR of p with q, and g1 and g2 are the two global optima.
q is the bit-wise exclusive OR of p with q, and g1 and g2 are the two global optima.
In the experiments that follow we will use the all-ones string as g1, and g2 = “010101…” (i.e. loci with an odd index take the value 0, and the even loci take the value 1). Thus the two optima have exactly 50% of bits in agreement and 50% complementary. The proofs of Theorems 2 through 4 are not valid for the function in Equation 4 – it should be clear that the recombinative hill-climber cannot succeed on this problem. However, if we re-introduce an adequate population we can recover a successful algorithm. Unfortunately, we are not able to prove a time to solution on this problem using a population. However, we will see that an estimate based on assumed invariants of the population gives reasonable times. Specifically, we use the rather heavy-handed assumption below. This assumption states explicitly that diversity is being maintained appropriately for recombination to work effectively. It supposes a level-wise discovery of blocks and that all members of the population progress together.
This estimate of the expected time for a GA on H-IFF takes no account of the population size, selection pressure, or any other aspect of the algorithm – all of these are embedded in Assumption 1. Nonetheless, our empirical results given in the next section give times to solution that are under this upper bound on expected time and accordingly, support the validity of the assumption for our experimental set-up.
5 EXPERIMENTAL RESULTS
5.1 VERIFYINGTHEOREM 4: RECOMBINATIVE HILL-CLIMBER WITH ONE-POINT CROSSOVER APPLIED TO H-IFF.
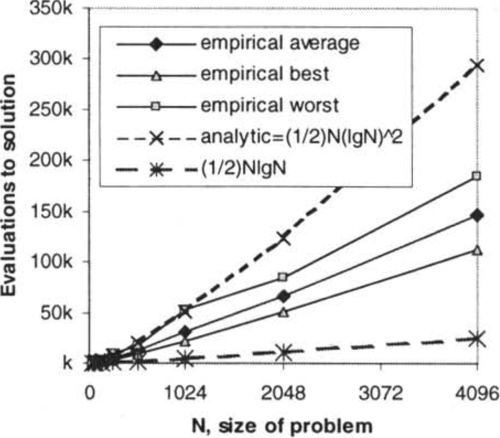
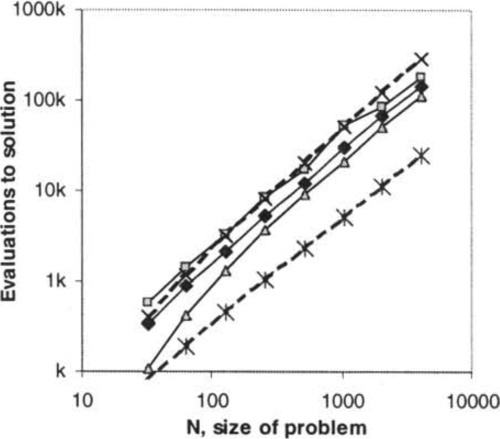
To validate Theorem 4 we implemented the algorithm of Figure 4 with one-point crossover. Figure 6a) shows the results of 30 runs on each problem size N = 32 doubling to N = 4096. All 30 runs were successful at every size. We show the fastest, the slowest and the mean time to find the solution from each N. The analytical time, T ≤ 1/2Nlg2N, provides a good upper bound. It appears to be too high by a factor less than lgN (see 1/2NlgN curve for comparison). Figure 6b) shows the same data on a log log plot.
5.2 VERIFYINGTHEOREM 5: GA WITH TWO-POINT CROSSOVER APPLIED TO H-IFF2
Theorem 5 is not based on any particular GA and empirically, we find that the algorithm in Figure 7, deterministic crowding, works faster and more reliably than GIGA on this problem. This is possibly because deterministic crowding (Mahfoud 1995) allows some convergence whilst also segregating competition and thereby maintaining diversity.

Pairing rule: if H(pl,cl) + H(p2,c2) < H(pl,c2) + H(p2,cl) then pair p1 with c1, and p2 with c2, else pair p1 with c2, and p2 with c1, where H gives the genotypic Hamming distance between two individuals.
Figure 8a) shows the solution times for the algorithm in Figure 4 for N = 32 doubling to N = 256 and for population sizes from 32 doubling to 4096. Average solution times over 30 runs are shown only for those population sizes that succeeded on at least 90% of runs (in an evaluation limit of 200 times the population size). For example, only the population size 4096 succeeded reliably on N = 256. We see that the time to solution is approximately linear with population size for those sizes that succeed. We also note that for each doubling of N, the minimum population size that succeeds reliably quadruples (See log log plot in Figure 8b).
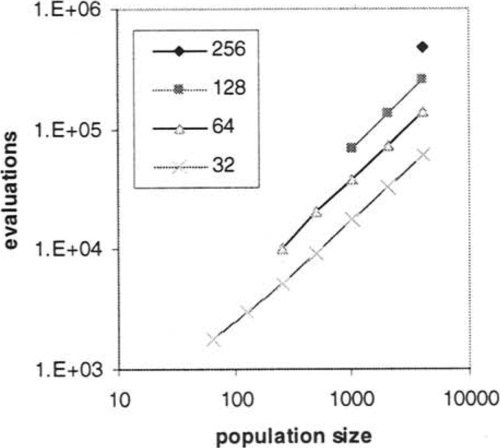
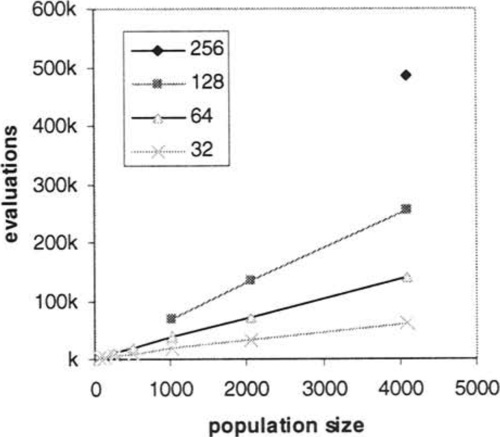
Since we are interested in whether there is any configuration for the GA such that time to solution is reliably better than our upper bound, we now focus on the smallest population size that succeeds reliably. We extract the average time to solution for each N using this population size, i.e. the first point on each curve. These points are compared with analytic time, from Theorem 5 in Figure 9a). This expected time, T ≤ 1/2N2lg2N, provides an overestimate of the experimental time. Figure 9b), shows the same data as 9a) on a log log plot.
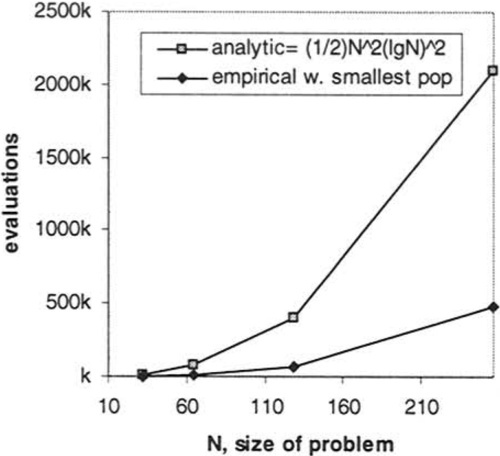
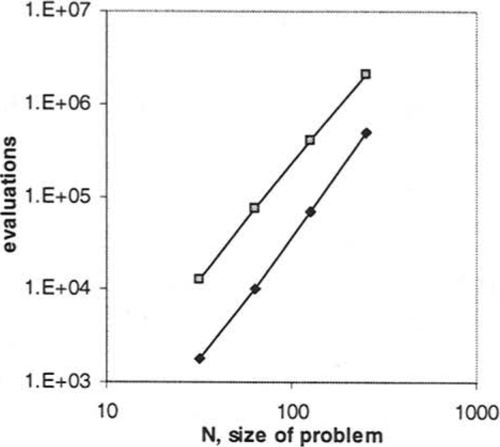
The fact that the empirical time is better than our analytic time does not necessarily mean that Assumption 1 was correct. However, we can make some statements about the operation of the algorithm from this result. Note that the algorithm uses elitist replacement; an individual can only be replaced by a new offspring if the new individual is fitter. An algorithm incorporating such a replacement strategy cannot succeed unless its variation operators successfully manipulate the search space so as to ensure that there is always at least one way in which a fitter individual can be created from the current population. Note also, that in H-IFF, since all blocks within a level are the same fitness, and higher level blocks must contain correct lowerlevel blocks, superior fitness can only arise from a greater number of correct blocks. Thus we know that since this algorithm succeeds then there must be a progression of individuals with monotonically increasing number of correct blocks, i.e. Condition 1 must be true. Further, we may say that an algorithm that performs better than our analytic time, as this algorithm does, either has more opportunities to find a next step on a path to the optimum, or has a shorter path than we than we thought. These observations suggest that the GA is able to properly exploit the decomposable structure of H-IFF by following the crossover landscape.
6 CONCLUSIONS
We have provided an analytic time to solution for a recombinative algorithm on a nonseparable building-block problem. The upper bound on expected time is based on proving a path to the optimum and the time for each step on the path. In the limited case of a population of two we have proved that the expected time to solution is at most O(Nlg2N), where N is the size of the problem in bits. This is verified empirically. For the more general population case we provide a time O(N21g2N) based on the assumption that, at any time, the state of the population is such that the algorithm is able to provide recombination steps that follow the path we have described.
This time estimate does not take account of population size (though we know empirically that time increases approximately linearly with population size for a given N). Instead, factors such as this are embedded into the assumption that the population is sufficient to provide recombinative steps. The empirical times therefore use the smallest population size (for each N) that succeeds reliably. In these cases it seems that there is a population size for which the GA succeeds reliably and our analytic time to solution is an overestimate.
These expected times are in contrast to the performance of mutation-based hill-climbers which either fail, or are not guaranteed to find solution in less than time exponential in N.
Our test problem does not involve difficult genetic linkage and the algorithm does not involve non-standard crossover operators – we use building-blocks with tight genetic linkage, and ordinary two-point crossover, as the Building-Block Hypothesis suggests. It is the epistatic linkage between building-blocks that makes the problem difficult for mutation, whereas an algorithm that is able to search combinations of building-blocks finds this problem easy. More specifically, the problem has a landscape with an exponential number of local optima for mutation, but in contrast, under the adaptive reorganisation of the landscape afforded by a population-based recombinative algorithm there are no local optima. Finally, our experimental results verify that the GA with crossover is able to properly exploit the hierarchically decomposable structure of this problem class and illustrate the potential value of recombination in more general non-separable problems.
Acknowledgements
Many thanks to Alden Wright for suggesting that H-IFF may yield to an adaptation of his analysis, and assisting with my preliminary analyses. Thanks also to the anonymous reviewers, and the members of DEMO at Brandeis especially Ofer Melnik, Anthony Bucci, and Jordan Pollack.