Towards a Theory of Strong Overgeneral Classifiers
Tim Kovacs [email protected] School of Computer Science University of Birmingham Birmingham B15 2TT United Kingdom
Abstract
We analyse the concept of strong overgeneral rules, the Achilles’ heel of traditional Michigan-style learning classifier systems, using both the traditional strength-based and newer accuracy-based approaches to rule fitness. We argue that different definitions of overgenerality are needed to match the goals of the two approaches, present minimal conditions and environments which will support strong overgeneral rules, demonstrate their dependence on the reward function, and give some indication of what kind of reward functions will avoid them. Finally, we distinguish fit overgeneral rules, show how strength and accuracy-based fitness differ in their response to fit overgenerals and conclude by considering possible extensions to this work.
1 INTRODUCTION
Learning Classifier Systems (LCS) typically use a Genetic Algorithm (GA) to evolve sets of if-then rules called classifiers to determine their behaviour in a problem environment. In Pittsburghstyle LCS the GA operates on chromosomes which are complete solutions (entire sets of rules), whereas in the more common Michigan-style LCS chromosomes are partial solutions (individual rules). In either case chromosome fitness is somehow determined by the performance of the LCS in a problem environment. We’ll consider LCS for reinforcement learning tasks, in which performance is measured by the amount of reward (a scalar) the environment gives the LCS. Precisely how to relate LCS performance to chromosome fitness has been the subject of much research, and is of great significance because adaptation of rules and LCS alike depends on it.
We undertake an analysis of the causes and effects of certain rule pathologies in Michigan LCS and trace them ultimately to the relation between LCS performance and rule fitness. We examine situations in which less desirable rules can achieve higher fitness than more desirable rules, which results in a mismatch between the goal of the LCS as a whole and the goal of the GA, since the goal of the GA is to find high-fitness rules.
We assume some familiarity with genetic algorithms, LCS, and Wilson’s XCS (Wilson, 1995), a new direction in LCS research. The most interesting feature of XCS is that it bases the fitness of rules on the accuracy with which they predict rewards, rather than the magnitude of rewards, as traditional LCS do. We call XCS an accuracy-based LCS to contrast it with traditional LCS, which we call strength-based LCS.
1.1 OVERGENERAL AND STRONG OVERGENERAL RULES
Dealing with overgeneral rules – rules which are simply too general – is a fundamental problem for LCS. Such rules may specify the desired action in a subset of the states they match, but, by definition, not in all states, so relying on them harms performance.
Another problem faced by some LCS is greedy classifier creation (Cliff and Ross, 1995; Wilson, 1994). To obtain better rules, an LCS’s GA allocates reproductive events preferentially to rules with higher fitness. Greedy classifier creation occurs in LCS in which the fitness of a rule depends on the magnitude of the reward it receives from the problem environment. In such systems rules which match in higher-rewarding parts of the environment will reproduce more than others. If the bias in reproduction of rules is strong enough there may be too few rules, or even no rules, matching low-rewarding states. (In the latter case, we say there’s a gap in the rules’ covering map of the input/action space.)
Cliff and Ross (1995) recognised that overgeneral rules can interact with greedy classifier creation, an effect Kovacs (2000) referred to as the problem of strong overgenerals. The interaction occurs when an overgeneral rule acts correctly in a high reward state and incorrectly in a low reward state. The rule is overgeneral because it acts incorrectly in one state, but at the same time it prospers because of greedy classifier creation and the high reward it receives in the other state. The proliferation of strong overgenerals can be disastrous for the performance of an LCS: such rules are unreliable, but outweigh more reliable rules when it comes to action selection. Worse, they may prosper under the influence of the GA, and may even reproduce more than reliable but low-rewarding rules, possibly driving them out of the population.
This work extends the analysis of strong overgenerals in (Kovacs, 2000) to show exactly what requirements must be met for them to arise in both strength and accuracy-based LCS. In order to compare the two approaches we begin by defining Goliath, a strength-based LCS which differs as little as possible from accuracy-based XCS, which allows us to isolate the effects of the fitness calculation on performance. We then argue that different definitions of overgenerality and strong overgenerality are appropriate for the two types of LCS. We later make a further, novel, distinction between strong and fit overgeneral rules. We present minimal environments which will support strong overgenerals, demonstrate the dependence of strong overgenerals on the reward function, and prove certain theorems regarding their prevalence under simplifying assumptions. We show that strength and accuracy-based fitness have different kinds of tolerance for biases (see section 3.5) in reward functions, and (within the context of various simplifying assumptions) to what extent we can bias them without producing strong overgenerals. We show what kinds of problems will not produce strong overgenerals even without our simplifying assumptions. We present results of experiments which show how XCS and Goliath differ in their response to fit overgenerals. Finally, we consider the value of the approach taken here and directions for further study.
2 BACKGROUND AND METHODOLOGY
2.1 LCS FOR REINFORCEMENT LEARNING
Reinforcement learning consists of cycles in which a learning agent is presented with an input describing the current environmental state, responds with an action and receives some reward as an indication of the value of its action. The reward received is defined by the reward function, which maps state/action pairs to the real number line, and which is part of the problem definition (Sutton and Barto, 1998). For simplicity we consider only single-step tasks, meaning the agent’s actions do not affect which states it visits in the future. The goal of the agent is to maximise the rewards it receives, and, in single-step tasks, it can do so in each state independently. In other words, it need not consider sequences of actions in order to maximise reward.
When an LCS receives an input it forms the match set [M] of rules whose conditions match the environmental input.1 The LCS then selects an action from among those advocated by the rules in [M]. The subset of [M] which advocates the selected action is called the action set [A]. Occasionally the LCS will trigger a reproductive event, in which it calls upon the GA to modify the population of rules.
We will consider LCS in which, on each cycle, only the rules in [A] are updated based on the reward received - rules not in [A] are not updated.
2.2 THE STANDARD TERNARY LCS LANGUAGE
A number of representations have been used with LCS, in particular a number of variations based on binary and ternary strings. Using what we’ll call the standard ternary LCS language each rule has a single condition and a single action. Conditions are fixed length strings from {0, 1, #}l, while rule actions and environmental inputs are fixed length strings from {0,1}l. In all problems considered here l = 1.
A rule’s condition c matches an environmental input m if for each character mi the character in the corresponding position ci is identical or the wildcard (#). The wildcard is the means by which rules generalise over environmental states; the more #s a rule contains the more general it is. Since actions do not contain wildcards the system cannot generalise over them.
2.3 STRENGTH-BASED AND ACCURACY-BASED FITNESS
Although the fitness of a rule is determined by the rewards the LCS receives when it is used, LCS differ in how they calculate rule fitness. In traditional strength-based systems (see, e.g., Goldberg, 1989; Wilson, 1994), the fitness of a rule is called its strength. This value is used in both action selection and reproduction. In contrast, the more recent accuracy-based XCS (Wilson, 1995) maintains separate estimates of rule utility for action selection and reproduction.
One of the goals of this work is to compare the way strength and accuracy-based systems handle overgeneral and strong overgeneral rules. To do so, we'll compare accuracy-based XCS with a strength-based LCS called Goliath which differs as little as possible from XCS, and which closely resembles Wilson's ZCS (Wilson, 1994). To be more specific, Goliath (in single-step tasks) uses the delta rule to update rule strengths:
Strength (a.k.a. prediction):
sj←sj+β(R−sj)
![]()
where sj is the strength of rule j, 0 < β ≤ 1 is a constant controlling the learning rate and R is the reward from the environment. Goliath uses the same strength value for both action selection and reproduction. That is, the fitness of a rule in the GA is simply its strength.
XCS uses this same update to calculate rule strength,2 and uses strength in action selection, but goes on to derive other statistics from it. In particular, from strength it derives the accuracy of a rule, which it uses as the basis of its fitness in the GA. This is achieved by updating a number of parameters as follows (see Wilson, 1995, for more). Following the update of a rule’s strength sj, we update its prediction error εj:
Prediction error:
εj←εj+β(|R−sj|Rmax−Rmin−εj)
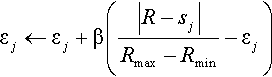
where Rmax and Rmin are the highest and lowest rewards possible in any state. Next we calculate the rule’s accuracy icy:
Accuracy:
kj={1ifεj<εoα(εj/εo)−votherwise
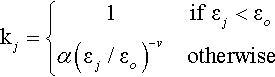
where 0 < εo is a constant controlling the tolerance for prediction error and 0 < α < 1 and 0 < v are constants controlling the rate of decline in accuracy when εo is exceeded. Once the accuracy of all rules in [A] has been updated we update each rule’s relative accuracy Kj@ #:
Relative accuracy:
K@#j←Kj∑x∈[A]Kx
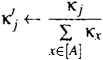
Finally, each rule’s fitness is updated:
Fitness:
Fj←Fj+β(K@#j−Fj)
![]()
To summarise, the XCS updates treat the strength of a rule as a prediction of the reward to be received, and maintain an estimate of the error εj in each rule’s prediction. An accuracy score Kj is calculated based on the error as follows. If error is below some threshold εo the rule is fully accurate (has an accuracy of 1), otherwise its accuracy drops off quickly. The accuracy values in the action set [A] are then converted to relative accuracies (the kj' update), and finally each rule’s fitness Fj is updated towards its relative accuracy.
To simplify, in XCS fitness is an inverse function of the error in reward prediction, with errors below εo being ignored entirely.
2.3.1 XCS, Goliath and other LCS
Goliath is not simply a straw man for XCS to outperform. It is a functional LCS, and is capable of solving some problems as well as any other LCS, including XCS. Goliath’s value is that we can study when and why it fails, and we can attribute any difference between its performance and that of XCS to the difference in fitness calculation.
Goliath differs from many other strength-based Michigan LCS in that it (following XCS) does not use any form of tax, and does not deduct rule “bids” from their strengths (see, e.g., Goldberg, 1989). See (Kovacs, 2001) for full details of both XCS and Goliath.
2.4 METHOD
LCS are complicated systems and analysis of their behaviour is often quite difficult. To make our analysis more tractable we’ll make a number of simplifications, perhaps the greatest of which is to study very small problems. Although very small, these problems illustrate different types of rules and the effects of different fitness definitions on them – indeed, they illustrate them better for their simplicity.
Another great simplification is to consider the much simpler case of single-step problems rather than multi-step ones. Multi-step problems present their own difficulties, but those present in the single-step case persist in the more complex multi-step case. We feel study of single-step problems can uncover fundamental features of the systems under consideration while limiting the complexity which needs to be dealt with.
To further simplify matters we’ll remove the GA from the picture and enumerate all possible classifiers for each problem, which is trivial given the small problems we’ll consider. Simplifying further still, we’ll consider only the expected values of rules, and not deviations from expectation. Similarly, we’ll consider steady state values, and not worry about how steady state values are reached (at least not until section 7). We’ll consider deterministic reward functions, although it would be easy to generalise to stochastic reward functions simply by referring to expected values. We’ll restrict our considerations to the standard ternary LCS language of section 2.2 because it is the most commonly used and because we are interested in fitness calculations and the ontology of rules, not in their representation. Finally, to simplify our calculations we’ll assume that, in all problem environments, states and actions are chosen equiprobably.
Removing the GA and choosing actions at random does not leave us with much of a classifier system. In fact, our simplifications mean that any quantitative results we obtain do not apply to any realistic applications of an LCS. Our results will, however, give us a qualitative sense of the behaviour of two types of LCS. In particular, this approach seems well suited to the qualitative study of rule ontology. Section 3 contains examples of this approach.
2.4.1 Default Hierarchies
Default Hierarchies (DHs) (see, e.g., Riolo, 1988; Goldberg, 1989; Smith, 1991) have traditionally been considered an important feature of strength-based LCS. XCS, however, does not support them because they involve inherently inaccurate rules. Although Goliath does not have this restriction, it does not encourage DHs, as some other LCS do, by, e.g., factoring rule specificity into action selection.
Consequently, default hierarchies have not been included in the analysis presented here, and their incorporation has been left for future work. DHs are potentially significant in that they may allow strength LCS to overcome some of the difficulties with strong overgeneral rules we will show them to have. If so, this would increase both the significance of DHs and the significance of the well-known difficulty of finding and maintaining them.
3 DEFINITIONS
3.1 CORRECT AND INCORRECT ACTIONS
Since the goal of our reinforcement learning agents is to maximise the rewards they receive, it’s useful to have terminology which distinguishes actions which do so from those which do not:
Correct action: In any given state the learner must choose from a set of available actions. A correct action is one which results in the maximum reward possible for the given state and set of available actions.
Incorrect action: One which does not maximise reward.
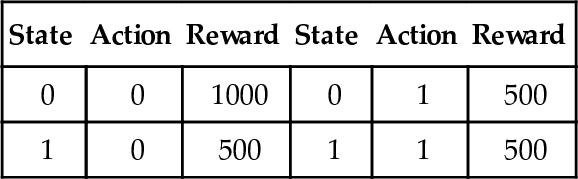
Table 1 defines a simple single-step test problem, in which for state 0 the correct action is 0, while in state 1 both actions 0 and 1 are correct. Note that an action is correct or incorrect only in the context of a given state, and the context of the rewards available in that state.
3.2 OVERGENERAL RULES
Table 2 shows all possible rules for the environment in table 1 using the standard ternary language of section 2.3. Each rule’s expected strength is also shown, using the simplifying assumption of equiprobable states and actions from section 2.4. The classification shown for each rule will eventually be explained in sections 3.2.2 and 3.2.3.
Table 2
All Possible Classifiers for the Simple Test Problem in Table 1 and their Classifications using Strength-Based and Accuracy-Based Fitness.
| Classifier | Condition | Action | E[Strength] | Strength Classification | Accuracy Classification |
| A | 0 | 0 | 1000 | Correct | Accurate |
| B | 0 | 1 | 500 | Incorrect | Accurate |
| C | 1 | 0 | 500 | Correct | Accurate |
| D | 1 | 1 | 500 | Correct | Accurate |
| E | # | 0 | 750 | Correct | Overgeneral |
| F | # | 1 | 500 | Overgeneral | Accurate |
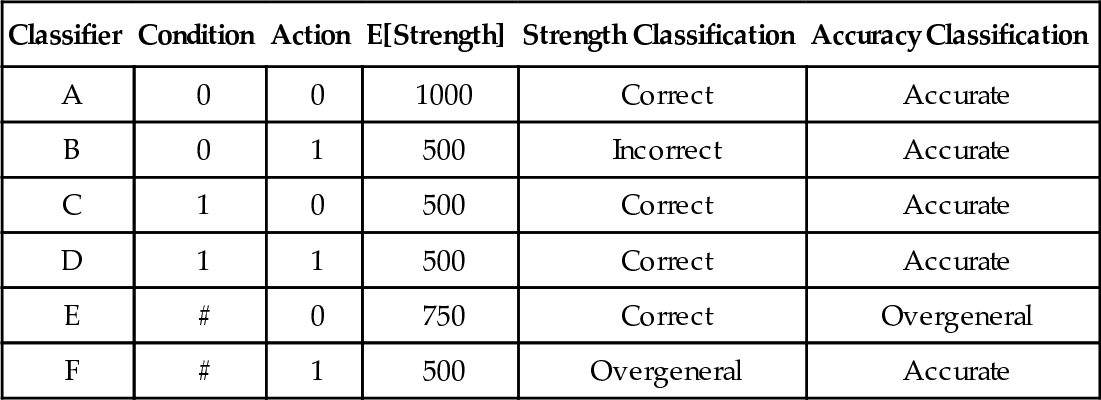
We’re interested in distinguishing overgeneral from non-overgeneral rules. Rules A,B,C and D are clearly not overgeneral, since they each match only one input. What about E and F? So far we haven’t explicitly defined overgenerality, so let’s make our implicit notion of overgenerality clear:
Overgeneral rule: A rule O from which a superior rule can be derived by reducing the generality of O’s condition.
This definition seems clear, but relies on our ability to evaluate the superiority of rules. That is, to know whether a rule X is overgeneral, we need to know whether there is any possible Y, some more specific version of X, which is superior to X. How should we define superiority?
3.2.1 Are Stronger Rules Superior Rules?
Can we simply use fitness itself to determine the superiority of rules? After all, this is the role of fitness in the GA. In other words, let’s say X is overgeneral if some more specific version Y is fitter than X.
In Goliath, our strength-based system, fitter rules are those which receive higher rewards, and so have higher strength. Let’s see if E and F are overgeneral using strength to define the superiority of rules.
Rule E. The condition of E can be specialised to produce A and C. C is inferior to E (it has lower strength) while A is superior (it has greater strength). Because A is superior, E is overgeneral.
This doesn’t seem right - intuitively E should not be overgeneral, since it is correct in both states it matches. In fact all three rules (A, C and E) advocate only correct actions, and yet A is supposedly superior to the other two. This seems wrong since E subsumes A and C, which suggests that, if any of the three is more valuable, it should be E.
Rule F. The condition of F can be specialised to produce B and D. Using strength as our value metric all three rules are are equally valuable, since they have the same expected strength, so F is not overgeneral.
This doesn’t seem right either – surely F is overgeneral since it is incorrect in state 0. Surely D should be superior to F since it is always correct.
Clearly using strength as our value metric doesn’t capture our intuitions about what the system should be doing.
To define the value of rules let’s return to the goal of the LCS, which, as mentioned earlier, is to maximise the reward it receives. Maximising reward means taking the correct action in each state. It is the correctness of its actions which determines a rule’s value, rather than how much reward it receives (its strength).
Recall from section 2.3 that strength is derived from environmental reward. Strength is a measure of how good – on average – a rule is at obtaining reward. Using strength as fitness in the GA, we will evolve rules which are – on average – good at obtaining reward. However, many of these rules will actually perform poorly in some states, and only achieve good average performance by doing particularly well in other states. Such rules are overgeneral; superior rules can be obtained by restricting their conditions to match only the states in which they do well.
To maximise rewards, we do not want to evolve rules which obtain the highest rewards possible in any state, but to evolve rules which obtain the highest rewards possible in the states in which they act. That is, rather than rules which are globally good at obtaining reward, we want rules which are locally good at obtaining reward. In other words, we want rules whose actions are correct in all states they match. What’s more, each state must be covered by a correct rule because an LCS must know how to act in each state. (In reinforcement learning terminology, we say it must have a policy.)
To encourage the evolution of consistently correct rules, rather than rules which are good on average, we can use techniques like fitness sharing. But, while such techniques may help, there remains a fundamental mismatch between using strength as fitness and the goal of evolving rules with consistently correct actions. See (Kovacs, 2000) for more.
3.2.2 Strength and Best Action Only Maps
To maximise rewards, a strength-based LCS needs a population of rules which advocates the correct action in each state. If, in each state, only the best action is advocated, the population constitutes a best action only map (Kovacs, 2000). While a best action only map is an ideal representation, it is still possible to maximise rewards when incorrect actions are also advocated, as long as they are not selected. This is what we hope for in practise.
Now let’s return to the question of how to define overgenerality in a strength-based system. Instead of saying X is overgeneral if some Y is fitter (stronger), let’s say it is overgeneral if some Y is more consistent with the goal of forming a best action only map; that is, if Y is correct in more cases than X.
Notice that we’re now speaking of the correctness of rules (not just the correctness of actions), and of their relative correctness at that. Let’s emphasise these ideas:
Fully Correct Rule: One which advocates a correct action in every state it matches.
Fully Incorrect Rule: One which advocates an incorrect action in every state it matches.
Overgeneral Rule: One which advocates a correct action in some states and an incorrect action in others (i.e. a rule which is neither fully correct nor fully incorrect).
Correctness of a Rule: The correctness of a rule is the proportion of states in which it advocates the correct action.3
The notion of the relative correctness of a rule allows us to say a rule Y is more correct (and hence less overgeneral) than a rule X, even if neither is fully correct.
Now let’s reevaluate E and F from table 2 to see how consistent they are with the goal of forming a best action only map. Rule E matches two states and advocates a correct action in both. This is compatible with forming a best action only map, so E is not overgeneral. Rule F also matches both states, but advocates an incorrect action in state 0, making F incompatible with the goal of forming a best action only map. Because a superior rule (D) can be obtain by specialising F, F is overgeneral.
Notice that we’ve now defined overgeneral rules twice: once in section 3.2 and once in this section. For the problems we’re considering here the two definitions coincide, although they do not always. For example, in the presence of perceptual aliasing (where an input to the LCS does not always describe a unique environmental state) a rule may be overgeneral by one definition but not by the other. That is, it may be neither fully correct nor fully incorrect, and yet it may be impossible to generate a more correct rule because a finer distinction of states cannot be expressed.
The above assumes the states referred to in the definition of overgenerality are environmental states. If we consider perceptual states rather than environmental states the rule is sometimes correct and sometimes incorrect in the same state (which is not possible in the basic environments studied here). We could take this to mean the rule is not fully correct, and thus overgeneral, or we might choose to do otherwise.
3.2.3 Accuracy and Complete Maps
While all reinforcement learners seek to maximise rewards, the approach of XCS differs from that of strength-based LCS. Where strength LCS seek to form best action only maps, XCS seeks to form a complete map: a set of rules such that each action in each state is advocated by at least one rule (Wilson, 1995; Kovacs, 2000). This set of rules allows XCS to approximate the entire reward function and (hopefully) accurately predict the reward for any action in any state. XCS’s fitness metric is consistent with this goal, and we’ll use it to define the superiority of rules for XCS.
The different approaches to fitness mean that while in strength-based systems we contrast fully correct, fully incorrect and overgeneral rules, with accuracy-based fitness we contrast accurate and inaccurate rules.
In XCS, fitter rules are those with lower prediction errors – at least up to a point: small errors in prediction are ignored, and rules with small enough errors are considered fully accurate (see the accuracy update in section 2.3). In other words, XCS has some tolerance for prediction error, or, put another way, some tolerance for changes in a rule’s strength, since changes in strength are what produce prediction error. We’ll use this tolerance for prediction error as our definition of overgenerality in XCS, and say that a rule is overgeneral if its prediction error exceeds the tolerance threshold, i.e. if εj ≥ εo. In XCS ‘overgeneral’ is synonymous with ‘not-fully-accurate’.
Although this work uses XCS as a model, we hope it will apply to other future accuracy-based LCS. To keep the discussion more general, instead of focusing on XCS and its error threshold, we’ll refer to a somewhat abstract notion of tolerance called τ. Let τ ≥ 0 be an accuracy-based LCS’s tolerance for oscillations in strength, above which a rule is judged overgeneral.
Like XCS’s error threshold, τ is an adjustable parameter of the system. This means that in an accuracy-based system, whether a rule is overgeneral or not depends on how we set τ. If τ is set very high, then both E and F from table 2 will fall within the tolerance for error and neither will be overgeneral. If we gradually decrease τ, however, we will reach a point where E is overgeneral while F is not. Notice that this last case is the reverse of the situation we had in section 3.2.2 when using strength-based fitness. So which rule is overgeneral depends on our fitness metric.
3.2.4 Defining Overgenerality
To match the different goals of the two systems we need different definitions of overgenerality:
Strength-based overgeneral: For strength-based fitness, an overgeneral rule is one which matches multiple states and acts incorrectly in some.4
Accuracy-based overgeneral: For accuracy-based fitness, an overgeneral rule is one which matches multiple states, some of which return (sufficiently) different rewards, and hence has (sufficiently) oscillating strength. Here a rule is overgeneral if its oscillations exceed τ.
Note that the strength definition requires action on the part of the classifiers while the accuracy definition does not. Thus we can have overgenerals in a problem which allows 0 actions (or, equivalently, 1 action) using accuracy (see, e.g., table 3), but not using strength.
3.3 STRONG OVERGENERAL RULES
Now that we’ve finally defined overgenerality satisfactorily let’s turn to the subject of strong overgenerality. Strength is used to determine a rule’s influence in action selection, and action selection is a competition between alternatives. Consequently it makes no sense to speak of the strength of a rule in isolation. Put another way, strength is a way of ordering rules. With a single rule there are no alternative orderings, and hence no need for strength.
In other words, strength is a relation between rules; a rule can only be stronger or weaker than other rules – there is no such thing as a rule which is strong in isolation. Therefore, for a rule to be a strong overgeneral, it must be stronger than another rule. In particular, a rule’s strength is relevant when compared to another rule with which it competes for action selection.
Now we can define strong overgeneral rules, although to do so we need two definitions to match our two definitions of overgenerality:
Strength-based strong overgeneral: A rule which sometimes advocates an incorrect action, and yet whose expected strength is greater than that of some correct (i.e. not-overgeneral) competitor for action selection.
Accuracy-based strong overgeneral: A rule whose strength oscillates unacceptably, and yet whose expected strength is greater than that of some accurate (i.e. not-overgeneral) competitor for action selection.
The intention is that competitors be possible, not that they need actually exist in a given population.
The strength-based definition refers to competition with correct rules because strength-based systems are not interested in maintaining incorrect rules (see section 3.2.2). This definition suits the analysis in this work. However, situations in which more overgeneral rules have higher fitness than less overgeneral – but still overgeneral – competitors are also pathological. Parallel scenarios exist for accuracy-based fitness. Such cases resemble the well-known idea of deception in GAs, in which search is lead away from desired solutions (see, e.g., Goldberg, 1989).
3.4 FIT OVERGENERAL RULES
In our definitions of strong overgenerals we refer to competition for action selection, but rules also compete for reproduction. To deal with the latter case we introduce the concept of fit overgerterals as a parallel to that of strong overgenerals. A rule can be both, or either. The definitions for strength and accuracy-based fit overgenerals are identical to those for strong overgenerals, except that we refer to fitness (not expected strength) and competition for reproduction (not action selection):
Strength-based fit overgeneral: A rule which sometimes advocates an incorrect action, and yet whose expected fitness is greater than that of some correct (i.e. not-overgeneral) competitor for reproduction.
Accuracy-based fit overgeneral: A rule whose strength oscillates unacceptably, and yet whose expected fitness is greater than that of some accurate (i.e. not-overgeneral) competitor for reproduction.
We won’t consider fit overgenerals as a separate case in our initial analysis since in Goliath any fit overgeneral is also a strong overgeneral.5 Later, in section 7, we’ll see how XCS handles both fit and strong overgenerals.
3.5 OTHER DEFINITIONS
For reference we include a number of other definitions:
Reward function: A function which maps state/action pairs to a numeric reward.
Constant function: A function which returns the same value regardless of its arguments. A function may be said to be constant over a range of arguments.
Unbiased reward function: One in which all correct actions receive the same reward.
Biased reward function: One which is not unbiased.
Best action only map: A population of rules which advocates only the correct action for each state.
Complete map: A population of rules such that each action in each state is advocated by at least one rule.
4 WHEN ARE STRONG OVERGENERALS POSSIBLE?
We’ve seen definitions for strong and fit overgeneral rules, but what are the exact conditions under which an environment can be expected to produce them? If such rules are a serious problem for LCS, knowing when to expect them should be a major concern: if we know what kinds of environment are likely to produce them (and how many) we’ll know something about what kinds of environment should be difficult for LCS (and how difficult).
Not surprisingly, the requirements for the production of strong and fit overgenerals depend on which definition we adopt. Looking at the accuracy-based definition of strong overgenerality we can see that we need two rules (a strong overgeneral and a not-overgeneral rule), that the two rules must compete for action selection, and that the overgeneral rule must be stronger than the not-overgeneral rule. The environmental conditions which make this situation possible are as follows:
1. The environment must contain at least two states, in order that we can have a rule which generalises (incorrectly).6
2. The environment may allow any number of actions in the two states, including 0 (or, equivalently, 1) action. (We’ll see later that strength-based systems differ in this respect.)
3. In order to be a strong overgeneral, the overgeneral must have higher expected strength than the not-overgeneral rule. For this to be the case the reward function must return different values for the two rules. More specifically, it must return more reward to the overgeneral rule.
4. The overgeneral and not-overgeneral rules must compete for action selection. This constrains which environments will support strong overgenerals.
The conditions which will support fit overgenerals are clearly very similar: 1) and 2) are the same, while for 3) the overgeneral must have greater fitness (rather than strength) than the not-overgeneral, and for 4) they must compete for reproduction rather than action selection.
4.1 THE REWARD FUNCTION IS RELEVANT
Let’s look at the last two requirements for strong overgenerals in more detail. First, in order to have differences in the expectations of the strengths of rules there must be differences in the rewards returned from the environment. So the values in the reward function are relevant to the formation of strong overgenerals. More specifically, it must be the rewards returned to competing classifiers which differ. So subsets of the reward function are relevant to the formation of individual strong or fit overgenerals.
In (Kovacs, 2000), having different rewards for different correct actions is called a bias in the reward function (see section 3.5). For strong or fit overgenerals to occur, there must be a bias in the reward function at state/action pairs which map to competing classifiers.
5 ACCURACY-BASED SYSTEMS
In section 4 we saw that, using the accuracy definition, strong overgenerals require an environment with at least two states, and that each state can have any number of actions. We also saw that the reward function was relevant but did not see exactly how. Now let’s look at a minimal strong overgeneral supporting environment for accuracy and see exactly what is required of the reward function to produce strong overgenerals. Table 3 shows a reward function for an environment with two states and one action and all possible classifiers for it. As always, the expected strengths shown are due to the simplifying assumption that states and actions occur equiprobably (section 2.4).
In section 2.4 we made a number of simplifying assumptions, and for now let’s make a further one: that there is no tolerance for oscillating strengths (τ = 0), so that any rule whose strength oscillates at all is overgeneral. This means rule E in table 3 is an overgeneral because it is updated towards different rewards. It is also a strong overgeneral because it is stronger than some not-overgeneral rule with which it competes, namely rule C. In section 4 we saw that strong overgenerals depend on the reward function returning more strength to the strong overgeneral than its not-overgeneral competitor. Are there reward functions under which E will not be a strong overgeneral? Since the strength of E is an average of the two rewards returned (labelled a and c in table 3 to correspond to the names of the fully specific rules which obtain them), and the strength of C is c, then as long as a > c, rule E will be a strong overgeneral. Symmetrically, if c > a then E will still be a strong overgeneral, in this case stronger than not-overgeneral rule A. The only reward functions which do not cause strong overgenerals are those in which a = c. So in this case any bias in the reward function makes the formation of a strong overgeneral possible.
If we allow some tolerance for oscillations in strength without judging a rule overgeneral, then rule E is not overgeneral only if a – c ≤ τ where τ is the tolerance for oscillations. In this case only reward functions in which a – c > τ will produce strong overgeneral rules.
5.1 A 2x2 ENVIRONMENT
We’ve just seen an example where any bias in the reward function will produce strong overgenerals. However, this is not the case when we have more than one action available, as in table 4. The strengths of the two fully generalised rules, E & F, are dependent only on the values associated with the actions they advocate. Differences in the rewards returned for different actions do not result in strong overgenerals – as long as we don’t generalise over actions, which was one of our assumptions from section 2.4.
5.2 SOME PROPERTIES OF ACCURACY-BASED FITNESS
At this point it seems natural to ask how common strong overgenerals are and, given that the structure of the reward function is related to their occurrence, to ask what reward functions make them impossible. In this section we’ll prove some simple, but perhaps surprising, theorems concerning overgeneral rules and accuracy-based fitness. However, we won’t go too deeply into the subject for reasons which will become clear later.
Let’s begin with a first approximation to when overgeneral rules are impossible:
More generally, strong overgenerals are impossible when the reward function is sufficiently close to constancy over each action that oscillations in any rule's strength are less than τ. Now we can see when strong overgenerals are possible:
In other words, if the rewards for the same action differ by more than τ the fully generalised rule for that action will be overgeneral. To avoid overgeneral rules completely, we’d have to constrain the reward function to be within i of constancy for each action. That overgeneral rules are widely possible should not be surprising. But it turns out that with accuracy-based fitness there is no distinction between overgeneral and strong overgeneral rules:
Taking theorems 2 and 3 together yields:
In short, using accuracy-based fitness and reasonably small x only a highly restricted class of reward functions and environments do not support strong overgeneral rules. These theorems hold for environments with more than 2 actions.
Note that the ‘for each action’ part of the theorems we’ve just seen depends on the inability of rules to generalise over actions, a syntactic limitation of the standard LCS language. If we remove this arbitrary limitation then we further restrict the class of reward functions which will not support strong overgenerals.
6 STRENGTH-BASED SYSTEMS
We’ve seen how the reward function determines when strong overgeneral classifiers are possible in accuracy-based systems. Now let’s look at the effect of the reward function using Goliath, our strength-based system. Recall from the strength-based definition of strong overgenerals that we need two rules (a strong overgeneral and a not-overgeneral correct rule), that the two rules must compete for action selection, and that the overgeneral rule must be stronger than the correct rule. The conditions which make this situation possible are the same as those for accuracy-based systems, except for a change to condition 2: there needs to be at least one state in which at least two actions are possible, so that the overgeneral rule can act incorrectly. (It doesn’t make sense to speak of overgeneral rules in a strength-based system unless there is more than one action available.)
A second difference is that in strength-based systems there is no tolerance for oscillations in a rule’s strength built into the update rules. This tolerance is simply not needed in Goliath where all that matters is that a rule advocate the correct action, not that its strength be consistent.
A complication to the analysis done earlier for accuracy-based systems is that strength-based systems tend towards best action only maps (see section 3 and Kovacs, 2000). Simply put, Goliath is not interested in maintaining incorrect rules, so we are interested in overgenerals only when they are stronger than some correct rule. For example, consider the binary state binary action environment of table 5. Using this unbiased reward function, rules E & F are overgenerals (since they are sometimes incorrect), but not strong overgenerals because the rules they are stronger than (B & C) are incorrect. (Recall from the definition of a strong overgeneral in a strength LCS in section 3.3 that the strong overgeneral must be stronger than a correct rule.) This demonstrates that in strength-based systems (unlike accuracy-based systems) not all overgeneral rules are strong overgenerals.
Table 5
A 2x2 Unbiased Reward Function and all its Classifiers.
| State | Action | Reward | State | Action | Reward |
| 0 | 0 | 1000 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1000 |
| Classifier | Condition | Action | E[Strength] | Status | |
| A | 0 | 0 | 1000 | Correct | |
| B | 0 | 1 | 0 | Incorrect | |
| C | 1 | 0 | 0 | Incorrect | |
| D | 1 | 1 | 1000 | Correct | |
| E | # | 0 | 500 | Overgeneral | |
| F | # | 1 | 500 | Overgeneral | |
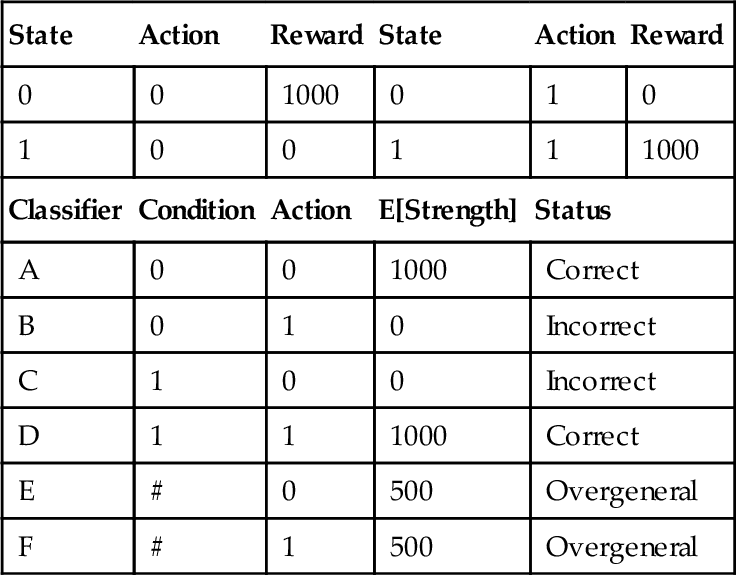
What consequence does this disinterest in incorrect rules have on the dependence of strong overgenerals on the reward function? The reward function in this example is not constant over either action, and the accuracy-based concept of tolerance does not apply. In an accuracy-based system there must be strong overgenerals under such conditions, and yet there are none in this example.
6.1 WHEN ARE STRONG OVERGENERALS IMPOSSIBLE IN A STRENGTH LCS?
Let’s begin with a first approximation to when strong overgenerals are impossible:
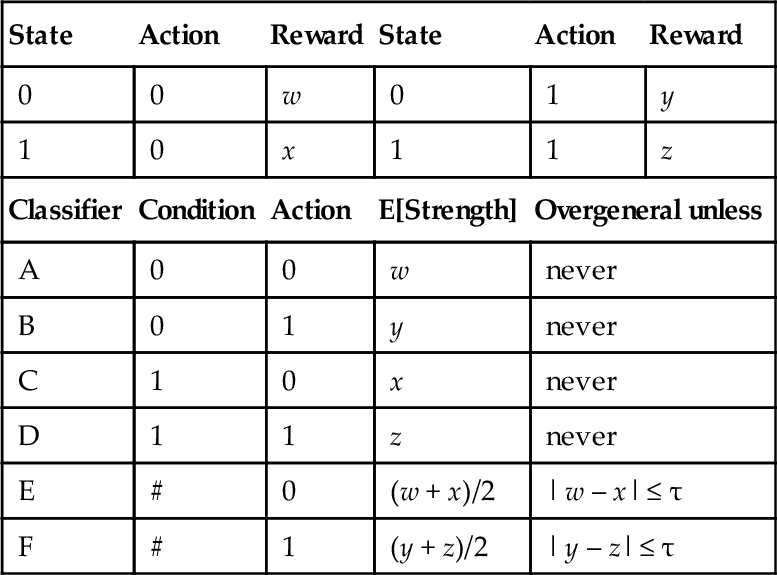
To make theorem 5 more concrete, reconsider the reward values in table 4. By definition, a correct action in a state is one which returns the highest reward for that state, so if we want w and z to be the only correct actions then w > y,z > x. If the reward function returns the same value for all correct actions then w = z. Then the strengths of the overgeneral rules are less than those of the correct accurate rules: E’s expected strength is (w + x)/2 which is less than A’s expected strength of wand F’s expected strength is (y + z)/2 which is less than D’s z, so the overgenerals cannot be strong overgenerals. (If w < y and z < x then we have a symmetrical situation in which the correct action is different, but strong overgenerals are still impossible.)
6.2 WHAT MAKES STRONG OVERGENERALS POSSIBLE IN STRENGTH LCS?
It is possible to obtain strong overgenerals in a strength-based system by defining a reward function which returns different values for correct actions. An example of a minimal strong overgeneral supporting environment for Goliath is given in table 6. Using this reward function, E is a strong overgeneral, as it is stronger than the correct rule D with which it competes for action selection (and for reproduction if the GA runs in the match set or panmictically (see Wilson, 1995)).
Table 6
A 2x2 Biased Reward Function which is a Minimal Strong Overgeneral Environment for Strength-Based LCS, and all its Classifiers.
| State | Action | Reward | State | Action | Reward |
| 0 | 0 | w = 1000 | 0 | 1 | y = 0 |
| 1 | 0 | x = 0 | 1 | 1 | z = 200 |
| Classifier | Condition | Action | E[Strength] | Strong overgeneral if | |
| A | 0 | 0 | w = 1000 | never | |
| B | 0 | 1 | y = 0 | never | |
| C | 1 | 0 | x = 0 | never | |
| D | 1 | 1 | z = 200 | never | |
| E | # | 0 | (w + x)/2 = 500 | (w + x)/2 > z | |
| F | # | 1 | (y + z)/2 = 100 | (y + z)/2 > z | |
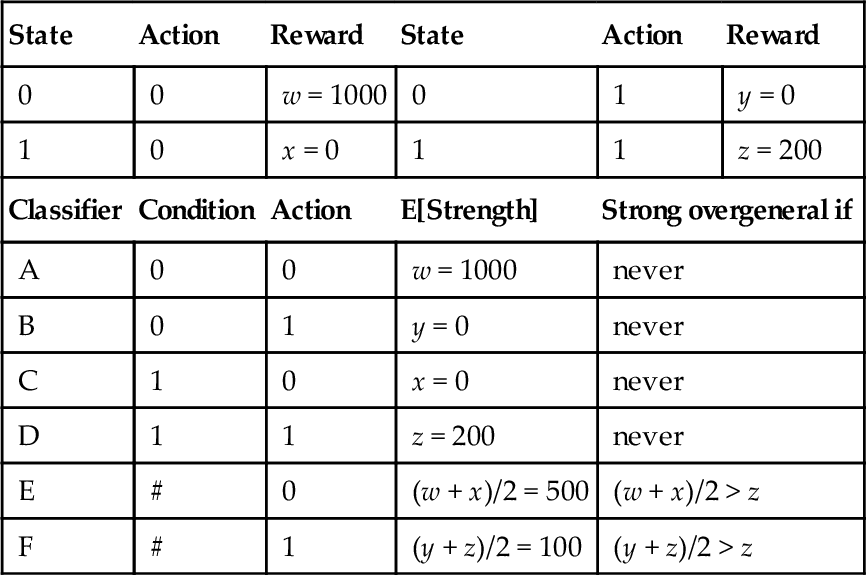
However, not all differences in rewards are sufficient to produce strong overgenerals. How much tolerance does Goliath have before biases in the reward function produce strong overgenerals? Suppose the rewards are such that w and z are correct (i.e. w > y,z > x) and the reward function is biased such that w > z. How much of a bias is needed to produce a strong overgeneral? I.e. how much greater than z must w be? Rule E competes with D for action selection, and will be a strong overgeneral if its expected strength exceeds D’s, i.e. if (w + x)/2 > z, which is equivalent to w > 2z – x. So a bias of w > 2z – x means E will be a strong overgeneral with respect to D, while a lesser bias means it will not.
E also competes with A for reproduction, and will be fitter than A if (w + x)/2 > w, which is equivalent to x > w. So a bias of x > w means E will be a fit overgeneral with respect to A, while a lesser bias means it will not. (Symmetrical competitions occur between F & A and F & D.)
We’ll take the last two examples as proof of the following theorem:
The examples in this section show there is a certain tolerance for differences in rewards within which overgenerals are not strong enough to outcompete correct rules. Knowing what tolerance there is is important as it allows us to design single-step reward functions which will not produce strong overgenerals. Unfortunately, because of the simplifying assumptions we’ve made (see section 2.4) these results do not apply to more realistic problems. However, they do tell us how biases in the reward function affect the formation of strong overgenerals, and give us a sense of the magnitudes involved. An extension of this work would be to find limits to tolerable reward function bias empirically. Two results which do transfer to more realistic cases are theorems 1 and 5, which tell us under what conditions strong overgenerals are impossible for the two types of LCS. These results hold even when our simplifying assumptions do not.
7 THE SURVIVAL OF RULES UNDER THE GA
We’ve examined the conditions under which strong overgenerals are possible under both types of fitness. The whole notion of a strong overgeneral is that of an overgeneral rule which can outcompete other, preferable, rules. But, as noted earlier, there are two forms of competition between rules: action selection and reproduction. Our two systems handle the first in the same way, but handle reproduction differently. In this section we examine the effect of the fitness metric on the survival of strong overgenerals.
XCS and Goliath were compared empirically on the environment in table 5. For these tests the GA was disabled and all possible rules inserted into the LCS at the outset. The following settings were used: β = 0.2, εo = 0.01 (see section 2.3). The number of cycles shown on the x-axes of the following figures indicates the number of explore cycles using Wilson’s pure explore/exploit scheme (Wilson, 1994), which is effectively the number of environmental inputs seen by the LCS.7
Figure 1 shows the fitness of each rule using strength (left) and accuracy (right), with results averaged over 100 runs. The first thing to note is that we are now considering the development of a rule’s strength and fitness over time (admittedly with the GA turned off), whereas until this section we had only considered steady state strengths (as pointed out in section 2.4). We can see that the actual strengths indeed converge towards the expected strengths shown in table 5. We can also see that the strengths of the overgeneral rules (E & F) oscillate as they are updated towards different values.
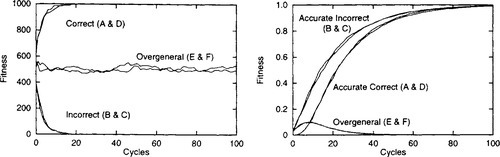
Using strength (figure 1, left), the correct rules A & D have highest fitness, so if the GA was operating we’d expect Goliath to reproduce them preferentially and learn to act correctly in this environment.
Using accuracy (figure 1, right), all accurate rules (A, B, C & D) have high fitness, while the overgenerals (E & F) have low fitness. Note that even though the incorrect rules (B & C) have high fitness and will survive with the GA operational, they have low strength, so they will not have much influence in action selection. Consequently we can expect XCS to learn to act correctly in this environment.
While both systems seem to be able to handle the unbiased reward function, compare them on the same problem when the reward function is biased as in table 6. Consider the results shown in figure 2 (again, averaged over 100 runs). Although XCS (right) treats the rules in the same way now that the reward function is biased, Goliath (left) treats them differently. In particular, rule E, which is overgeneral, has higher expected strength than rule D, which is correct, and with which it competes for action selection. Consequently E is a strong overgeneral (and a fit overgeneral if E and D also compete for reproduction).
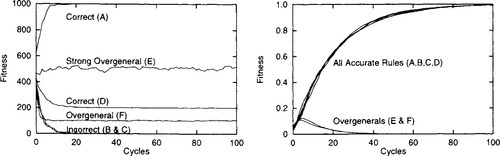
These trivial environments demonstrate that accuracy-based fitness is effective at penalising overgeneral, strong overgeneral, and fit overgeneral rules. This shouldn’t be surprising: for accuracy, we’ve defined overgeneral rules precisely as those which are less than fully accurate. With fitness based on accuracy these are precisely the rules which fare poorly.
With Goliath’s use of strength as fitness, strong overgenerals are fit overgenerals. But with XCS’s accuracy-based fitness, strong overgenerals – at least those encountered so far – have low fitness and can be expected to fare poorly. It is unknown whether XCS can suffer from fit overgenerals, but it may be possible if we suitably bias the variance in the reward function.
8 DISCUSSION
We’ve analysed and extended the concept of overgeneral rules under different fitness schemes. We consider dealing with such rules a major issue for Michigan-style evolutionary rule-based systems in general, not just for the two classifier systems we have considered here. For example, the use of alternative representations (e.g. fuzzy classifiers), rule discovery systems (e.g. evolution strategies) or the addition of internal memory should not alter the fundamental types of rules which are possible. In all these cases, the system would still be confronted with the problems of greedy classifier creation, overgeneral, strong overgeneral, and fit overgeneral rules. Only by modifying the way in which rule fitness is calculated, or by restricting ourselves to benign reward functions, can we influence which types of rules are possible.
Although we haven’t described it as such, this work has examined the fitness landscapes defined by the reward function and the fitness scheme used. We can try to avoid pathological fitness landscapes by choosing suitable fitness schemes, which is clearly essential if we are to give evolutionary search the best chance of success. This approach of altering the LCS to fit the problem seems more sensible than trying to alter the problem to fit the LCS by using only reward functions which strength LCS can handle.
8.1 EXTENSIONS AND QUANTITATIVE ANALYSIS
We could extend the approach taken in this work by removing some of the simplifying assumptions we made in section 2.4 and dealing with the resultant additional complexity. For example, we could put aside the assumption of equiprobable states and actions, and extend the inequalities showing the requirements of the reward function for the emergence of strong overgenerals to include the frequencies with which states and actions occur. Taken far enough such extensions might allow quantitative analysis of non-trivial problems. Unfortunately, while some extensions would be fairly simple, others would be rather more difficult.
At the same time, we feel the most significant results from this approach are qualitative, and some such results have already been obtained: we have refined the concept of overgenerality (section 3.2), argued that strength and accuracy-based LCS have different goals (section 3.2), and introduced the concept of fit overgenerals (section 3.4).
We’ve seen that, qualitatively, strong and fit overgenerals depend essentially on the reward function, and that they are very common. We’ve also seen that the newer accuracy-based fitness has, so far, dealt with them much better than Goliath’s more traditional strength-based fitness (although we have not yet considered default hierarchies). This is in keeping with the analysis in section 3.2.1 which suggests that using strength as fitness results in a mismatch between the goals of the LCS and its GA.
Rather than pursue quantitative results we would prefer to extend this qualitative approach to consider the effects of default hierarchies and mechanisms to promote them, and the question of whether persistent strong and fit overgenerals can be produced under accuracy-based fitness. Also of interest are multi-step problems and hybrid strength/accuracy-based fitness schemes, as opposed to the purely strength-based fitness of Goliath and purely accuracy-based fitness of XCS.
Acknowledgements
Thank you to Manfred Kerber and the anonymous reviewers for comments, and to the organisers for their interest in classifier systems. This work was funded by the School of Computer Science at the University of Birmingham.