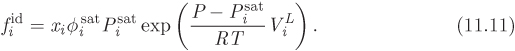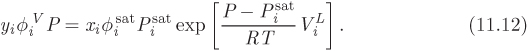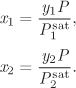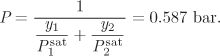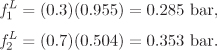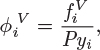Chapter 11. Ideal Solution

In the previous chapter we developed the general criteria for phase equilibrium and showed how the phase diagram and all other properties of a mixture can be calculated if the equation of state is known. In all property calculations that are based on equations of state we are starting from the ideal-gas state and use the equation of state to calculate residual properties, in effect, to extrapolate from the ideal gas to the actual state of the system. This approach works quite well for mixtures of nonpolar molecules whose interactions are captured accurately by cubic equations of state. Mixtures of strongly interacting molecules cannot be described by these methods with sufficient accuracy.¹ A different approach is needed to do calculations with these systems. Instead of using the ideal-gas state as the starting point to describe a liquid mixture, we use a state closer to the liquid itself: the ideal solution. In this chapter we define the ideal solution, identify systems that can be described under the simplified assumptions of the ideal-solution theory, and calculate their phase diagram.

1. Several adaptations of equations of state are now available that can be applied to strongly interacting systems. These are beyond the scope of this book. The interested reader may consult Ref. [3].

The learning objectives for this chapter are to:

1. Define the ideal solution.

2. Obtain equations for the primary properties (volume, enthalpy, entropy) of ideal solution.

3. Obtain the fugacity of component in ideal solution.

4. Calculate the phase diagram of ideal solutions using Raoult’s law.

11.1 Ideality in Solution

In a pure liquid all interactions are between molecules of the same kind. In solution, molecules are surrounded by a mix of similar and dissimilar molecules. The behavior of the solution is ultimately determined by the balance of self- and cross-interactions. A special case of practical and theoretical importance is when cross- and self-interactions are identical in magnitude. This situation arises when molecules are very similar in chemical nature and size, as in solutions of neighboring members of a homologous series. We call this special system an ideal solution. The ideal solution is defined by the following properties:

where the superscript ^id is used to refer to “ideal solution.” Because molecules that form ideal solutions interact with each other in the same manner as among themselves, there is no change of volume or enthalpy when the pure components are mixed to form the solution. The entropy, on the other hand, does not remain constant but increases by exactly the same amount as when ideal gases mix. There is a close relationship between ideal solutions and ideal mixtures, but an important difference as well: in the ideal-gas mixture, self-interactions and cross-interactions are both zero; in ideal solution, self- and cross-interactions are of equal strength, but they are not zero. In fact, they are quite strong, as a result of the close proximity of molecules in the liquid. The ideal-gas mixture, therefore, should be thought of as a special case of ideal solution. It has the properties of the ideal-solution, eqs. (11.1)–(11.3) but also additional special properties (for example, it obeys the ideal-gas law) that the ideal solution does not have.

Equations (11.1)–(11.3) give the primary properties of mixing. All other properties may be obtained by their relationship to those given above. In particular, for the internal energy and Gibbs free energy we obtain

which are obtained by writing U^id = H^id − PV^id, and G^id = H^id − TS^id. From these equations we may easily identify the corresponding partial molar properties:

The most important partial molar property is the chemical potential. It is the partial molar Gibbs free energy and is given by

Here, is the chemical potential of component in ideal solution, and G_i is the chemical potential (molar Gibbs free energy) of the pure liquid at the same temperature and pressure.

11.2 Fugacity in Ideal Solution

The key problem is to calculate the phase diagram of ideal solution and for this we first need an expression for fugacity. We start with the basic relationship between fugacity and chemical potential in eq. (10.18). Taking state A to be component i in ideal solution, and state B the pure component at the same temperature and pressure, we have

where we use eq. (11.9) to write the result on the far right. Solving for f_i we obtain the following simple expression:

This states that the fugacity of component in ideal solution is the product of the pure-component fugacity, and the mol fraction of component in solution. This equation is known as the Lewis-Randall rule and is the basis for VLE calculations with ideal solutions.

For the fugacity of pure liquid at the temperature and pressure of the solution we use the Poynting equation, which relates this fugacity to the fugacity of the saturated liquid at same temperature:

where is the saturation pressure, is the fugacity coefficient of the saturated pure component, and is the molar volume of the pure liquid. Then, the fugacity in ideal solution takes the form,

Here, except for the mol fraction, all other properties in the right-hand side refer to pure liquid i.

11.3 VLE in Ideal Solution–Raoult’s Law

To perform VLE calculations with ideal solutions, we begin with the equilibrium condition that requires the fugacity of component i to be the same in the liquid and in the vapor:

For the fugacity of the liquid we use eq. (11.11); for the fugacity of the component in the vapor we use the general expression, Combining these expressions, the equilibrium criterion now takes the form,

Here, is the fugacity coefficient of component i in the vapor, not to be confused with , which refers to the saturated pure component i at the same temperature. This result takes a much simpler form if pressure is relatively low. Then, the Poynting correction can be neglected and the fugacity coefficients may be set to 1. With these simplifications, eq. (11.12) becomes

This is known Raoult’s law and requires only the saturation pressure of the pure components. The assumptions that make this simple equation valid are that the total pressure and the saturation pressure of component i be sufficiently low. Raoult’s law should be understood as a shortcut for quick calculations.

In a binary mixture, Raoult’s law gives

These two equations, along with the normalization conditions for the mol fractions,

x₁ + x₂ = 1,

y₁ + y₂ = 1,

constitute four equations that relate the following six variables:

{x₁, x₂, y₁, y₂, P, T}.

Temperature appears implicitly in the saturation pressure of pure component, which is assumed to be known as a function of temperature, usually via the Antoine equation, or some similar temperature-dependent expression. The six unknowns and four equations result in two degrees of freedom.² The typical problems are classified as “bubble T or P,” “dew T or P,” or “flash.” These classifications were introduced in Chapter 10 and are summarized again in Table 11-1. Solution strategies for performing these calculations are outlined below.

2. The same result is reached through application of the phase rule: with two components (N = 2) and two phases (π = 2), the degrees of freedom are F = N + 2 – π = 2.

Table 11-1: Classification of VLE Problems

Bubble P Calculation

Following the designation of VLE problems introduced in Chapter 10, in the bubble P problem we know temperature and the composition of the liquid and seek pressure and the composition of the vapor. Adding eqs. (11.14) and (11.15) to eliminate the unknown vapor fractions we obtain the bubble pressure of the solution:

The vapor mol fractions are then calculated from eqs. (11.14) and (11.15):

where P is the bubble pressure calculated above. Notice that according to eq. (11.16), the bubble pressure of an ideal solution is an average of the saturation pressures of the pure components.

Bubble T Calculation

In this case we know liquid composition and total pressure, and seek to calculate vapor composition and temperature. Again we add eqs. (11.14) and (11.15) to eliminate the unknown vapor fractions:

In this equation, the unknown is temperature, which appears implicitly in the saturation pressure through an equation such as the Antoine. Because this is a nonlinear equation in T, it requires a numerical solution. Once temperature is known, the saturation pressures are calculated and the vapor mole fractions are obtained as before, using

Dew P Calculation

Here the knowns are temperature and the composition of the vapor, and we seek to calculate pressure and the composition of liquid. We begin by solving eqs. (11.14) and (11.15) for the unknown mol fractions:

Adding these equations we eliminate the unknown compositions and obtain an equation that is solved for the dew pressure:

Once the dew pressure is known, the liquid mole fractions are obtained from eqs. (11.18) and (11.19).

Dew T Calculation

In this problem we know pressure and the composition of the vapor, and seek temperature and the composition of the liquid. As in the previous case, we first solve Raoult’s law for the liquid mol fractions to obtain eqs. (11.18) and (11.18), then add them to obtain

This equation is solved for the unknown dew temperature. Once T is known, the saturation pressures are calculated and the mole fractions of the liquid are obtained by substitution into Raoult’s law.

Flash Calculation

In flash separations, a mixture of known overall composition is brought into the two-phase region and the resulting liquid and vapor are separated into two streams whose composition is given by the tie line that corresponds to the temperature and pressure in the separator. Calculations are streamlined by making use of the K factors. These were defined in Chapter 8 as K_i = y_i/x_i, and in the case of ideal solution are given by

Using the K factors, Raoult’s law is written as

In addition, we have the mass balance between feed and the liquid and vapor streams at the exit:

where L and V are the fractions of liquid and vapor. Equations (11.23)–(11.26), along with the normalization conditions for the mole fractions, constitute the available equations of the flash problem. The corresponding variables are:

z_i, x_i, y_i, L, V, P, T.

For a binary system this leads to three degrees of freedom, which means that three independent variables must be specified for the problem to be well-defined.³ The solution procedure will then depend on which variables are known and which must be solved for.

3. Including the three normalization conditions (for z_i, x_i, and y_i) we have seven equations and 10 unknowns, or three degrees of freedom. In this case, in addition to the two degrees for vapor-liquid equilibrium of binary mixture we have one additional degree of freedom for the material balance between inlet and outlet of the separator.

11.4 Energy Balances

Energy balances involving ideal solutions require the internal energy (closed system) or the enthalpy (open system), both of which are given by straightforward expressions in terms of the corresponding properties of the pure liquids at the pressure and temperature of the solution:

For processes that do not involve change of composition, the change of the solution enthalpy is

where ΔH_i is the enthalpy change of the pure liquid between the pressure and temperature of the initial and final state. If the process involves no phase change, the term ΔH_i may be calculated by integration of the liquid heat capacity between the initial (T₁) and final (T₂) temperatures:⁴

4. Since pressure makes negligible contribution to the enthalpy of liquids, this equation may be used even if the pressure changes between initial and final states.

Alternatively, ΔH_i may be calculated from tabulated values, or from an appropriate equation of state. The internal energy of the solution is calculated in a similar manner.⁵

5. Alternatively, once the enthalpy change is known, the internal energy of component i is

ΔU_i = ΔH_i − Δ(PV_i) ≈ ΔH_i,

where Δ(PV_i) is the difference in the product PV_i between the initial and final state and is usually small enough to be negligible.

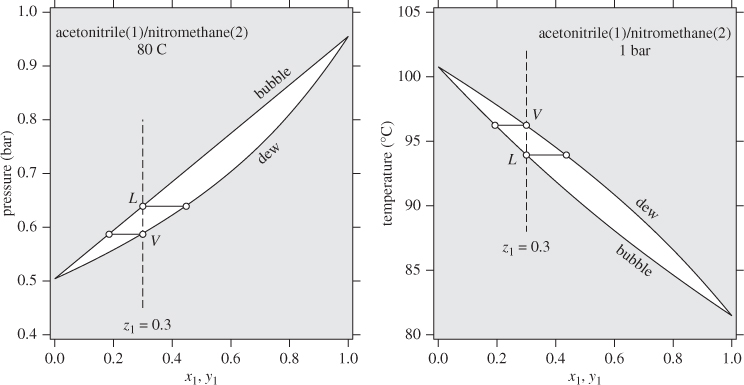
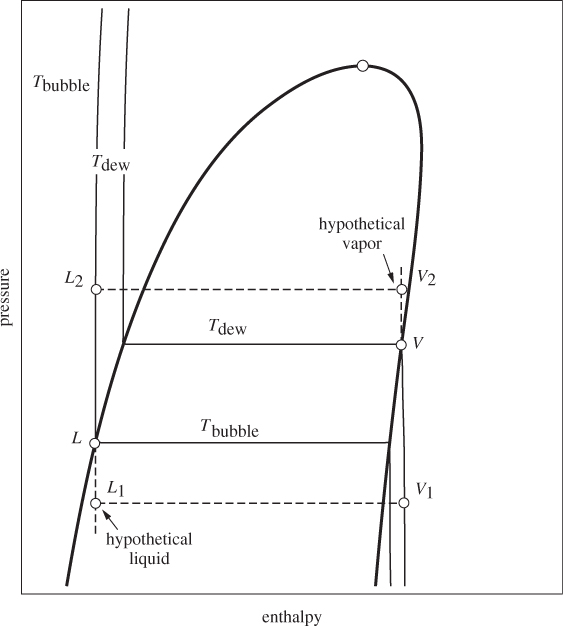
For processes that involve phase transformation, the general approach is to use the ideal-solution equation for the enthalpy of the liquid and treat the vapor phase as an ideal-gas mixture. This reduces the problem to a calculation of the enthalpies of pure liquid and pure vapor components. If the calculation involves states near the phase boundary, hypothetical states may be involved, whose properties must be calculated by extrapolation from known real states. As an example, consider the constant-pressure heating of a solution that contains 30% acetonitrile in nitromethane, at 1 bar. This is shown by the line LV on the Txy graph in Figure 11-1. The enthalpy change for this process is

where H_dew is the enthalpy of the vapor at the dew point and H_bubble is the enthalpy of the liquid in the bubble point. The enthalpy of the liquid calculated by the ideal-solution equation,

H_bubble = z₁H_L1 + z₂H_L2,

where z_i is the composition of the liquid and H_Li is the enthalpy of pure liquid i at the bubble temperature and pressure P, the fixed pressure of the process. Treating the vapor as an ideal-gas mixture, its enthalpy is

H_dew = z₁H_V1 + _z2H_V2,

where H_Vi is the enthalpy of pure vapor of component i at the dew temperature and pressure P. Taking the difference between the two expressions, the enthalpy change between the bubble and dew point is

The problem, therefore, is reduced to the calculation of enthalpy changes of pure components. Notice that two of the states involved in this equation are hypothetical: pure acetonitrile at the bubble temperature of the solution is a vapor; and pure nitromethane is liquid at the dew temperature of the mixture. Accordingly, H_L1 refers to the enthalpy of a hypothetical liquid at T_bubble, P, and H_V2 refers to a hypothetical vapor at T_dew, P. The properties of these hypothetical states may be approximated as those of the corresponding saturated phases: H_L1 is taken to be the enthalpy of the pure saturated liquid at T_bubble, and H_V2 as the enthalpy of the pure saturated vapor at T_dew.

11.5 Noncondensable Gases

When only a single component is present (pure fluid), below the boiling temperature the system is liquid, and above it vapor. When two liquids are mixed to form a solution, then a component produces a vapor over a range of temperatures, from the bubble point to the dew point. This range is expanded even further if the second component is a gas above its critical temperature. We refer to such a gas as noncondensable to emphasize the fact that it does not undergo a vapor-liquid transition as long as temperature remains above the critical point. For example, pure water⁶ at 1 atm cannot exist as vapor below 100 °C but in the presence of air it produces vapor even at room temperature. The presence of a noncondensable gas alters the phase behavior of a system, even when the gas itself has negligible solubility in the liquid. In reality, gases have a finite solubility in the liquid and they participate in phase equilibrium by partitioning between both phases. This problem will be discussed in Chapter 13. However, under pressures and temperatures near ambient, the solubility of most gases in liquids is low and it is an acceptable approximation to assume that the liquid phase contains only the condensable species.

6. By “pure water” we mean a system that contains only water but no other substance. We may visualize such experiment by placing liquid water in a cylinder with a piston and moving the piston to touch the free surface of the liquid so that no gas is present.

Suppose that an ideal solution of two components (i = 1, 2) is in the presence of a noncondensable gas (subscript g). Neglecting the solubility of the gas in the liquid, the liquid contains only the liquid components while the gas contains the noncondensable gas well as vapors of the liquid components. The vapor/liquid equilibrium of the condensable components is described by Raoult’s law:

along with the normalization conditions

The only difference here is that the normalization condition of the gas-phase mole fractions must include the noncondensable species. It is the presence of the noncondensable species that allows the condensable components to form a vapor and establish vapor/liquid equilibrium. If it is absent, vapor/liquid equilibrium can be established only when the following equation is satisfied:

When the noncondensable gas is present, this equation becomes⁷

7. Multiply eq. (11.32) by the total pressure P, then substitute eqs. (11.29), (11.30) into the result.

and can be satisfied even when because air “fills in” the difference.

Applications–Humidification

In humidification we are dealing with a single condensable species (water) in the presence of a noncondensable gas (air). As a condensable species, water obeys Raoult’s law:⁸

8. A pure liquid is a special case of an ideal solution since all interactions are of the same strength (self-interactions).

Since the solubility of air is neglected, the mol fraction of water in the liquid is 1 and the above equation simplifies to

This equation states that the partial pressure of water vapor in the presence of liquid water is equal to the saturation pressure of pure water at this temperature. Equation 11.33, along with the normalization condition, fully specify the problem (y_a stands for the mole fraction of air). The relative humidity, RH, is defined as the ratio of the partial pressure of water vapor in air relative to the saturation pressure of water at the same temperature.

If RH < 1, the air is unsaturated in water vapor. If RH = 1, it is saturated, that is, it holds the maximum amount of water vapor that is possible at the given pressure and temperature. The relative humidity of unsaturated air can be increased by manipulating any of the factors in the above equation: by bringing more water vapor into the system (increasing y_w), by increasing pressure, or by decreasing temperature (causes the saturation pressure to decrease). Once the system becomes saturated (RH = 1), it reaches the dew point. Attempting to increase the relative humidity past this point causes enough vapor to condense so as to keep the relative humidity equal to 1. The dew point, of the gas is defined by the condition RH = 1, or

which in thermodynamic language expresses the fact that fugacity of water in the liquid () is equal to the fugacity of water in the vapor (y_wP). The solution of problems based on these equations is demonstrated in the examples that follow. Although the discussion is for water in air, the same ideas apply to any condensable species in the presence of a noncondensable gas.

11.6 Summary

The ideal solution is a useful idealization that simplifies VLE calculations of systems composed of molecules whose cross interactions are nearly identical to their self interactions. It is an idealization because such similarity is encountered only in an approximate sense. It is very useful because several real systems are actually well approximated by ideal solutions. When this is the case, a property of the mixture can be calculated solely from the properties of the pure components and the amounts of components. The VLE problem, in particular, is very straightforward and reduces to Raoult’s law. Compared to calculations that are based on equations of state, calculations with ideal solutions are very simple and require no interaction parameters or mixing rules. This simplicity comes with the limitation that ideal-solution theory works with a small number of systems whose self- and cross-interactions are similar. The true value of the ideal solution is that it provides the basis for treating more complex solutions through the introduction of excess properties. This approach is discussed in the next chapter.

11.7 Problems

Problem 11.1: A vapor mixture of acetone (1) and nitromethane (2) (y₁ = 0.7) initially at P = 1 bar and 110 °C is to be liquified by compression under constant temperature.

a) At what pressure does the system fully become a liquid?

b) Calculate the composition of the last bubble that condenses.

c) What is the fugacity of nitromethane in the liquid when the system is at the conditions of part (a)?

Assume that the system behaves according to Raoult’s law. The saturation pressures of pure acetone and nitromethane at 110 °C are 463 kPa, and 132.4 kPa respectively.

Problem 11.2: A mixture contains n-pentane, n-hexane, and n-heptane at equal mole fractions. The temperature is 55 °C.

a) Calculate the bubble and dew pressure at 55 °C.

b) What is the phase of the system at 1.7 bar, 55 °C? If a two-phase system, calculate the amount and composition of each phase.

c) Repeat the previous part at 0.5 bar.

d) The pressure is adjusted so that 75% of the mixture is vapor while the temperature remains at 55 °C. Determine the pressure and the compositions of the two phases.

Additional data: At 55 °C the saturation pressures of n-C₅, n-C₆, and n-C₇ are 1.903 bar, 0.644 bar, and 0.231 bar respectively.

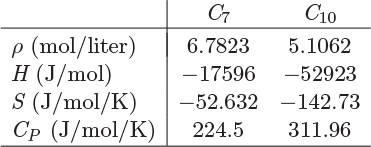
Problem 11.3: a) Calculate the enthalpy, entropy, and volume of a solution that contains 37.5% by mole heptane in decane, at 15 °C, 1 bar.

b) Calculate the amount of heat needed to raise the temperature of the solution to 40 °C under constant pressure of 1 bar.

c) Calculate the entropy change of the solution in part b.

Additional data: You may assume that the components form an ideal solution. The following properties of the pure components at 15 °C, 1 bar are known:

Problem 11.4: Assuming normal heptane and normal octane to form ideal solutions, do the following:

a) Calculate the chemical potential of n-C₇(1) in solution with n-C₈(2) at 40 °C, 1 bar, x₁ = 0.45. The reference state is the pure liquid at 40 °C, 1 bar.

b) Calculate the fugacity of normal heptane at the conditions of part (a).

c) Calculate the bubble pressure of the solution (x₁ = 0.45) at 40 °C.

d) Calculate the dew pressure of the solution at 40 °C.

e) Calculate the bubble temperature at 1 bar.

f) Calculate the dew temperature at 1 bar.

g) Calculate the amount and composition of vapor and liquid when a solution with z₁ = 0.45 is flashed to 40 °C, 0.065 bar.

Problem 11.5: A tank that contains a mixture of normal heptane (1)/normal octane is delivered to you. The composition of the mixture is unknown but the tank labels state that the bubble temperature of the mixture at 1 bar is 103 °C.

a) What is the composition of the mixture?

b) What is the dew temperature at 1 bar?

c) The mixture is to be flashed at 120 °C, 1.5 bar. Determine the recovery of normal heptane in the vapor stream.

d) You are requested to flash the mixture so that the liquid stream is 85% of the inlet (by mol). If the pressure is 1.5 bar, what temperature should be used?

Additional data: The saturation pressures of the two components are given by the Antoine equation:

where P^sat is in mm Hg, t is in Kelvin, and the parameters A_i, B_i, C_i, are

Problem 11.6: a) A stream contains a mixture of 40% normal heptane (by mol) and 60% toluene. Calculate the bubble and dew pressure of the mixture at 120 °C.

b) You are requested to adjust the volatility of the mixture so that the bubble pressure at 120 °C is 4 bar. You may add either normal pentane or normal octane. Which component will you add and in what amount? Report the amount as mol of additive per mole of the original solution.

c) Regardless of your answer in part (b), your supervisor instructs you to add 0.2 moles of normal octane per mol of solution. This new stream is flashed and the vapor and liquid streams are separated. The available information for the streams in the separator are shown below. Fill out the missing entries and determine the pressure:

Additional information: The saturation pressures at 120 °C are: P_pentane = 9.2 bar, P_heptane = 1.8 bar, P_octane = 1.1 bar, P_toluene = 1.0 bar.

Problem 11.7: Assuming toluene (1) and heptane (2) to form ideal solutions, answer the following:

a) A solution of the two components that contains 62% mol toluene is slowly heated at constant pressure. When the solution begins to boil the temperature reads 120 °C. What is the pressure?

b) The bubble pressure at 120 °C of a mixture of the two components is 2 bar. What is the dew pressure of this mixture at 120 °C?

c) A mixture of toluene and heptane that contains 61% by mole toluene is at 120 °C, 2.45 bar. What is the fugacity of toluene in this mixture?

Additional data: The saturation pressures of the pure components at 120 °C are: ,

Problem 11.8: You have just been delivered a tank containing a mixture of n-butane (83.3% by mol) and n-octane at 25 °C and 1 bar. Your boss asks you to measure the viscosity of the mixture, so you have to take a sample for analysis. One technician (twice your age, and smiling) says you should collect the sample in a test tube because the contents are in the liquid phase. Another technician (three times your age, also smiling) says you should use a balloon because the contents of the tank are in the vapor phase. A third technician is looking at you waiting for your instructions. This is your first day on the job. What do you do?

State all your assumptions and justify your reasoning with calculations—this is no time for wrong decisions!

Additional data: The saturation pressures of the components at 25 °C are: n-butane: 2.34 bar; n-octane: 0.0175 bar

Problem 11.9: Assuming the system methanol(1)/ethanol(2) to form ideal solutions, do the following:

a) Calculate the bubble and dew pressure at 100 °C of a mixture that contains 20% methanol by mol.

b) Construct a Pxy graph at 100 °C.

c) Construct a Txy graph at 1.2 bar.

d) A stream that contains a methanol/ethanol mixture with 32% mol methanol is flashed to 100 °C to a pressure such that the molar rate of the vapor stream is 75% of the feed. Determine the temperature and the composition of the two phases. The Antoine equation for the pure components are given below:

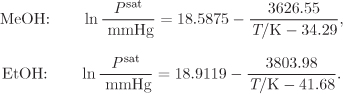
Problem 11.10: a) A solution contains 25% by mol methanol in ethanol. The pressure is reduced at constant temperature T = 85 °C until the first bubble appears. What is the composition of that bubble?

b) We continue to reduce the pressure until the last drop evaporates. What is the composition of that drop?

Use the data in Problem 11.9.

Problem 11.11: A mixture contains 82% by mol nitromethane in acetonitrile. Determine the phase of the system at the conditions given below. If the system is in the vapor-liquid region, report the fraction of each phase.

a) 85 °C, 1 bar.

b) 120 °C, 2.7 bar.

Additional data: Assume the components to form an ideal solution. The saturation pressures for the pure components are given below.

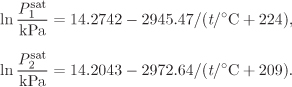
Problem 11.12: a) Assuming that methanol (1), ethanol (2), acetonitrile (3), and nitromethane (4), form ideal solutions, calculate the bubble and dew pressure at 120 °C of a mixture that contains equal moles of each of the four components.

b) What is the phase of this mixture at 1 bar, 120 °C?

Additional data: the saturation pressures are: P₁ = 6.43239 bar, P₂ = 4.34246 bar, P₃ = 3.02411 bar, P₄ = 1.75725 bar.

Problem 11.13: The exhaust stream from a combustion process contains 10% water vapor (by mol). The pressure of the stream is 2 bar and the temperature 100 °C.

a) What is the relative humidity of the stream?

b) What is its dew temperature?

c) The stream is to be cooled to 25 °C at constant pressure. To avoid condensation, the exhaust stream is mixed with dry air prior to cooling. How much air is needed? Report the result in moles of dry air per mole of gas.

Problem 11.14: The pressure is 1 bar, the relative humidity is 75%, and the dew temperature is 25 °C.

a) What is the mol fraction of water vapor in the air?

b) What is the temperature?

c) Your dehumidifier removes water vapor from air by cooling the air to 12 °C.

What fraction of water vapor is removed from the air?

d) What is the dew temperature of the air at the exit of the dehumidifier?

e) State and justify all your assumptions clearly.

Problem 11.15: a) A solution that contains nitromethane in acetonitrile is heated at constant pressure of 1 bar until the first bubble appears. If the temperature at this point is 85 °C, what is the composition of the original solution?

b) You are delivered a mixture of nitromethane in acetonitrile. The composition is not known but you are told that the dew temperature at 1 bar is 93.5 °C. What is the phase at 111 °C, 2 bar?

Problem 11.16: At 80 °C, 1.32 bar the system methanol(1)/ethanol(2) is in vapor-liquid equilibrium. The composition of the two phases is x₁ = 0.25, y₁ = 0.37. Calculate the fugacity, fugacity coefficient of each component in each phase. You may assume that the vapor phase is in the ideal-gas state.