9
Optimal Inference and Alternatives to the QMLE*
The most commonly used estimation method for GARCH models is the QML method studied in Chapter 7. One of the attractive features of this method is that the asymptotic properties of the QMLE are valid under mild assumptions. In particular, no moment assumption is required on the observed process in the pure GARCH case. However, the QML method has several drawbacks, motivating the introduction of alternative approaches. These drawbacks are the following: (i) the estimator is not explicit and requires a numerical optimisation algorithm; (ii) the asymptotic normality of the estimator requires the existence of a moment of order 4 for the noise η t ; (iii) the QMLE is inefficient in general; (iv) the asymptotic normality requires the existence of moments for ε t in the general ARMA–GARCH case; and (v) a complete parametric specification is required.
In the ARCH case, the QLS estimator defined in Section 6.2 addresses point (i) satisfactorily, at the cost of additional moment conditions. The maximum likelihood (ML) estimator studied in Section 9.1 of this chapter provides an answer to points (ii) and (iii), but it requires knowledge of the density f of η t . Indeed, it will be seen that adaptive estimators for the set of all the parameters do not exist in general semi‐parametric GARCH models. Concerning point (iii), it will be seen that the QML can sometimes be optimal outside of trivial case where f is Gaussian. In Section 9.2, the ML estimator will be studied in the (quite realistic) situation where f is mis‐specified. It will also be seen that the so‐called local asymptotic normality (LAN) property allows us to show the local asymptotic optimality of test procedures based on the ML. In Section 9.3, less standard estimators are presented in order to address to some of the points (i)–(v).
In this chapter, we focus on the main principles of the estimation methods and do not give all the mathematical details. Precise regularity conditions justifying the arguments used can be found in the references that are given throughout the chapter or in Section 9.4.
9.1 Maximum Likelihood Estimator
In this section, the density
f
of the strong white noise (η
t
) is assumed known. This assumption is obviously very strong and the effect of the mis‐specification of
f
will be examined in Section 9.2 . Conditionally on the
σ
‐field ℱ
t − 1
generated by {ε
u
: u < t}, the variable ε
t
has the density
x → σ
t
−1
f(x/σ
t
). It follows that, given the observations ε1,…, ε
n
, and the initial values ![]() , the conditional likelihood is defined by
, the conditional likelihood is defined by
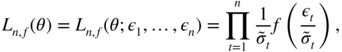
where ![]() is recursively defined, for
t ≥ 1, by
is recursively defined, for
t ≥ 1, by

A maximum likelihood estimator (MLE) is obtained by maximising the likelihood on a compact subset Θ*
of the parameter space. Such an estimator is denoted by ![]() .
.
9.1.1 Asymptotic Behaviour
Under the above‐mentioned regularity assumptions, the initial conditions are asymptotically negligible and, using the ergodic theorem, we have almost surely

using Jensen's inequality and the fact that

Adapting the proof of the consistency of the QMLE, it can be shown that ![]() almost surely as
n → ∞.
almost surely as
n → ∞.
Assuming in particular that θ 0 belongs to the interior of the parameter space, a Taylor expansion yields

We have

It is easy to see that (ν t , ℱ t ) is a martingale difference (using, for instance, the computations of Exercise 9.1). It follows that
where ℑ is the Fisher information matrix, defined by

Note that
ζ
f
is equal to
σ
2
times the Fisher information for the scale parameter
σ > 0 of the densities
σ
−1
f(⋅/σ). When
f
is the ![]() (0,1) density, we thus have
ζ
f
= σ
2 × 2/σ
2 = 2.
(0,1) density, we thus have
ζ
f
= σ
2 × 2/σ
2 = 2.
We now turn to the other terms of the Taylor expansion (9.2). Let
We have
thus, using the invertibility of ℑ ,
Note that
With the previous notation, the QMLE has the asymptotic variance

The following proposition shows that the QMLE is not only optimal in the Gaussian case.
Note that when f is of the form ( 9.9) then we have

up to a constant which does not depend on θ . It follows that in this case the MLE coincides with the QMLE, which entails the sufficient part of Proposition 9.1.
9.1.2 One‐Step Efficient Estimator
Figure 9.1 shows the graph of the family of densities for which the QMLE and MLE coincide (and thus for which the QML is efficient). When the density f does not belong to this family of distributions, we have ζ f (∫x 4 f(x)dx − 1) > 4, and the QMLE is asymptotically inefficient in the sense that


Figure 9.1 Density ( 9.9) for different values of a > 0. When η t has this density, the QMLE and MLE have the same asymptotic variance.
is positive definite. Table 9.1 shows that the efficiency loss can be important.
Table 9.1
Asymptotic relative efficiency (ARE) of the MLE with respect to the QMLE, ![]() , when
, when ![]() , where
f
ν
denotes the Student
t
density with
ν
degrees of freedom.
, where
f
ν
denotes the Student
t
density with
ν
degrees of freedom.
| ν | 5 | 6 | 7 | 8 | 9 | 10 | 20 | 30 | ∞ |
| ARE | 5/2 | 5/3 | 7/5 | 14/11 | 6/5 | 15/13 | 95/92 | 145/143 | 1 |
An efficient estimator can be obtained from a simple transformation of the QMLE, using the following result (which is intuitively true by (9.7)).
In practice, one can take the QMLE as a preliminary estimator: ![]() .
.
9.1.3 Semiparametric Models and Adaptive Estimators
In general, the density
f
of the noise is unknown, but
f
and
f
′
can be estimated from the normalised residuals ![]() ,
t = 1,…, n
(for instance, using a kernel non‐parametric estimator). The estimator
,
t = 1,…, n
(for instance, using a kernel non‐parametric estimator). The estimator ![]() (or the one‐step estimator
(or the one‐step estimator ![]() ) can then be utilised. This estimator is said to be adaptive if it inherits the efficiency property of
) can then be utilised. This estimator is said to be adaptive if it inherits the efficiency property of ![]() for any value of
f
. In general, it is not possible to estimate all the GARCH parameters adaptively.
for any value of
f
. In general, it is not possible to estimate all the GARCH parameters adaptively.
Take the ARCH(1) example

where η t has the double Weibull density
The subscript 0 is added to signify the true values of the parameters. The parameter ![]() , where
θ
0 = (ω
0, α
0)′
, is estimated by maximising the likelihood of the observations ε1,…, ε
n
conditionally on the initial value ε0
. In view of (9.3), the first two components of the score are given by
, where
θ
0 = (ω
0, α
0)′
, is estimated by maximising the likelihood of the observations ε1,…, ε
n
conditionally on the initial value ε0
. In view of (9.3), the first two components of the score are given by

with
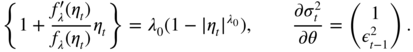
The last component of the score is

Note that

where γ = 0.577… is the Euler constant. It follows that the score satisfies

where

and ![]() . By the general properties of an information matrix (see Exercise 9.4 for a direct verification), we also have
. By the general properties of an information matrix (see Exercise 9.4 for a direct verification), we also have
The information matrix ℑ being such that ℑ 12 ≠ 0, the necessary Stein's condition (see Bickel 1982) for the existence of an adaptive estimator is not satisfied. The intuition behind this condition is the following. In view of the previous discussion, the asymptotic variance of the MLE of ϑ 0 should be of the form

When
λ
0
is unknown, the optimal asymptotic variance of a regular estimator of
θ
0
is thus
ℑ
11
. Knowing
λ
0
, the asymptotic variance of the MLE of
θ
0
is ![]() . If there exists an adaptive estimator for the class of the densities of the form
f
λ
(or for a larger class of densities), then we have
. If there exists an adaptive estimator for the class of the densities of the form
f
λ
(or for a larger class of densities), then we have ![]() . Since
. Since ![]() (see Exercise 6.7), this is possible only if
ℑ
12 = 0, which is not the case here.
(see Exercise 6.7), this is possible only if
ℑ
12 = 0, which is not the case here.
Reparameterising the model, Drost and Klaassen (1997) showed that it is, however, possible to obtain adaptive estimates of certain parameters. To illustrate this point, return to the ARCH(1) example with the parameterisation

Let ϑ = (α, c, λ) be an element of the parameter space. The score now satisfies

Thus ![]() with
with

where

It can be seen that this matrix is invertible because its determinant is equal to ![]() . Moreover,
. Moreover,

The MLE enjoying optimality properties in general, when λ 0 is unknown, the optimal variance of an estimator of (α 0, c 0) should be equal to

When λ 0 is known, a similar calculation shows that the MLE of (α 0, c 0) should have the asymptotic variance

We note that ![]() . Thus, in presence of the unknown parameter
c
, the MLE of
α
0
is equally accurate when
λ
0
is known or unknown. This is not particular to the chosen form of the density of the noise, which leads us to think that there might exist an estimator of
α
0
that adapts to the density
f
of the noise (in presence of the nuisance parameter
c
). Drost and Klaassen (1997) showed the actual existence of adaptive estimators for some parameters of an extension of (9.12).
. Thus, in presence of the unknown parameter
c
, the MLE of
α
0
is equally accurate when
λ
0
is known or unknown. This is not particular to the chosen form of the density of the noise, which leads us to think that there might exist an estimator of
α
0
that adapts to the density
f
of the noise (in presence of the nuisance parameter
c
). Drost and Klaassen (1997) showed the actual existence of adaptive estimators for some parameters of an extension of (9.12).
9.1.4 Local Asymptotic Normality
In this section, we will see that the GARCH model satisfies the so‐called LAN property, which has interesting consequences for the local asymptotic properties of estimators and tests. Let ![]() be a sequence of local parameters around the parameter
be a sequence of local parameters around the parameter ![]() , where (h
n
) is a bounded sequence of ℝ
p + q + 1
. Consider the local log‐likelihood ratio function
, where (h
n
) is a bounded sequence of ℝ
p + q + 1
. Consider the local log‐likelihood ratio function

The Taylor expansion of this function around 0 leads to
where, as we have already seen,
It follows that
The properties (9.13)–(9.14) are called LAN. It entails that the MLE is locally asymptotically optimal (in the minimax sense and in various other senses; see van der Vaart 1998). The LAN property also makes it very easy to compute the local asymptotic distributions of statistics, or the asymptotic local powers of tests. As an example, consider tests of the null hypothesis
against the sequence of local alternatives
The performance of the Wald, score, and of likelihood ratio tests will be compared.
Wald Test Based on the MLE
Let ![]() be the (q + 1)th component of the MLE
be the (q + 1)th component of the MLE ![]() . In view of ( 9.7) and ( 9.13)–( 9.14), we have under
H
0
that
. In view of ( 9.7) and ( 9.13)–( 9.14), we have under
H
0
that
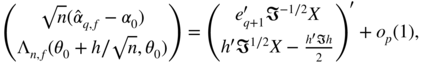
where ![]() , and
e
i
denotes the
ith vector of the canonical basis of ℝ
p + q + 1
, noting that the (q + 1)th component of
, and
e
i
denotes the
ith vector of the canonical basis of ℝ
p + q + 1
, noting that the (q + 1)th component of ![]() is equal to
α
0
. Consequently, the asymptotic distribution of the vector defined in (9.15) is
is equal to
α
0
. Consequently, the asymptotic distribution of the vector defined in (9.15) is

Le Cam's third lemma (see van der Vaart 1998, p. 90; see also Exercise 9.3) and the contiguity of the probabilities ![]() and
and ![]() (implied by the LAN properties ( 9.13)–( 9.14)) show that, for
(implied by the LAN properties ( 9.13)–( 9.14)) show that, for ![]() ,
,
The Wald test (and also the
t
test) is defined by the rejection region ![]() where
where
and ![]() denotes the (1 − α
)‐quantile of a chi‐square distribution with 1 degree of freedom. This test has asymptotic level
α
and local asymptotic power
denotes the (1 − α
)‐quantile of a chi‐square distribution with 1 degree of freedom. This test has asymptotic level
α
and local asymptotic power ![]() , where Φ
c
(⋅) denotes the cumulative distribution function of a non‐central chi‐square with 1 degree of freedom and non‐centrality parameter
1
, where Φ
c
(⋅) denotes the cumulative distribution function of a non‐central chi‐square with 1 degree of freedom and non‐centrality parameter
1

This test is locally asymptotically uniformly most powerful among the asymptotically unbiased tests.
Score Test Based on the MLE
The score (or Lagrange multiplier) test is based on the statistic

where ![]() is the MLE under
H
0
, that is, constrained by the condition that the (q + 1)th component of the estimator is equal to
α
0
. By the definition of
is the MLE under
H
0
, that is, constrained by the condition that the (q + 1)th component of the estimator is equal to
α
0
. By the definition of ![]() , we have
, we have

In view of (9.17) and (9.18), the test statistic can be written as

Under
H
0
, almost surely ![]() and
and ![]() . Consequently,
. Consequently,

and

Taking the difference, we obtain

which, using ( 9.17), gives
From (9.20), we obtain

Using this relation, ![]() and ( 9.18), it follows that
and ( 9.18), it follows that

Using (9.19), we have
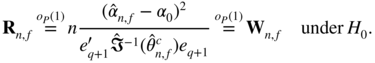
By Le Cam's third lemma, the score test thus inherits the local asymptotic optimality properties of the Wald test.
Likelihood Ratio Test Based on the MLE
The likelihood ratio test is based on the statistic ![]() . The Taylor expansion of the log‐likelihood around
. The Taylor expansion of the log‐likelihood around ![]() leads to
leads to

thus, using ![]() , (9.5) and (9.21),
, (9.5) and (9.21),
under H 0 and H n . It follows that the three tests exhibit the same asymptotic behaviour, both under the null hypothesis and under local alternatives.
Tests Based on the QML
We have seen that the W n, f , R n, f , and L n, f tests based on the MLE are all asymptotically equivalent under H 0 and H n (in particular, they are all asymptotically locally optimal). We now compare these tests to those based on the QMLE, focusing on the QML Wald whose statistic is
where ![]() is the (q + 1)th component of the QML
is the (q + 1)th component of the QML ![]() , and
, and ![]() is
is

or an asymptotically equivalent estimator.
Recall that

Using ( 9.13)–( 9.14), (9.8), and Exercise 9.2, we obtain

under H 0 . The previous arguments, in particular Le Cam's third lemma, show that
The local asymptotic power of the ![]() test is thus
test is thus ![]() , where the non‐centrality parameter is
, where the non‐centrality parameter is

Figure 9.2 displays the local asymptotic powers of the two tests, ![]() (solid line) and
(solid line) and ![]() (dashed line), when
f
is the normalised Student
t
density with 5 degrees of freedom and when
θ
0
is such that
(dashed line), when
f
is the normalised Student
t
density with 5 degrees of freedom and when
θ
0
is such that ![]() . Note that the local asymptotic power of the optimal Wald test is sometimes twice as large as that of score test.
. Note that the local asymptotic power of the optimal Wald test is sometimes twice as large as that of score test.

Figure 9.2
Local asymptotic power of the optimal Wald test  (solid line) and of the standard Wald test
(solid line) and of the standard Wald test  (dotted line), when
(dotted line), when  and
ν = 5.
and
ν = 5.
9.2 Maximum Likelihood Estimator with Mis‐specified Density
The MLE requires the (unrealistic) assumption that
f
is known. What happens when
f
is mis‐specified, that is, when we use ![]() with
h ≠ f
?
with
h ≠ f
?
In this section, the usual assumption ![]() will be replaced by alternative moment assumptions that will be more relevant for the estimators considered. Under some regularity assumptions, the ergodic theorem entails that
will be replaced by alternative moment assumptions that will be more relevant for the estimators considered. Under some regularity assumptions, the ergodic theorem entails that

Here, the subscript f is added to the expectation symbol in order to emphasise the fact that the random variable η 0 follows the distribution f , which does not necessarily coincide with the ‘instrumental’ density h . This allows us to show that
Note that the estimator ![]() can be seen as a non‐Gaussian QMLE.
can be seen as a non‐Gaussian QMLE.
9.2.1 Condition for the Convergence of  to
θ
0
to
θ
0
Note that under suitable identifiability conditions, σ t (θ 0)/σ t (θ) = 1 if and only if θ = θ 0 . For the consistency of the estimator (that is, for θ * = θ 0 ), it is thus necessary for the function σ → E f g(η 0, σ), where g(x, σ) = log σh(xσ), to have a unique maximum at 1:
It is sometimes useful to replace condition (9.25) by one of its consequences that is easier to handle. Assume the existence of
If there exists a neighborhood
V(1) of 1 such that ![]() the dominated convergence theorem shows that ( 9.25) implies the moment condition
the dominated convergence theorem shows that ( 9.25) implies the moment condition
Obviously, condition ( 9.25) is satisfied for the ML, that is, when h = f (see Exercise 9.5), and also for the QML, as the following example shows.
The following example shows that for condition ( 9.25) to be satisfied, it is sometimes necessary to reparameterise the model and to change the identifiability constraint Eη 2 = 1.
The previous examples show that a particular choice of
h
corresponds to a natural identifiability constraint. This constraint applies to a moment of
η
t
(![]() when
h
is
when
h
is ![]() , and
E ∣ η
t
∣ = 1 when
h
is Laplace). Table 9.3 gives the natural identifiability constraints associated with various choices of
h
. When these natural identifiability constraints are imposed on the GARCH model, the estimator
, and
E ∣ η
t
∣ = 1 when
h
is Laplace). Table 9.3 gives the natural identifiability constraints associated with various choices of
h
. When these natural identifiability constraints are imposed on the GARCH model, the estimator ![]() can be interpreted as a non‐Gaussian QMLE, and converges to
θ
0
, even when
h ≠ f
.
can be interpreted as a non‐Gaussian QMLE, and converges to
θ
0
, even when
h ≠ f
.
Table 9.3
Identifiability constraint under which ![]() is consistent.
is consistent.
| Law | Instrumental density h | Constraint |
| Gaussian |

|
|
| Double gamma |
|
|
| Laplace |
|
E ∣η t ∣ = 1 |
| Gamma |
|
|
| Double inverse gamma |
|
|
| Double inverse χ 2 |
|
|
| Double Weibull |
|
E|η t | λ = 1 |
| Gaussian generalised |
|
E|η t | λ = 1 |
| Inverse Weibull |
|
E|η t |−λ = 1 |
| Double log‐normal |

|
E log ∣η t ∣ = m |
9.2.2 Convergence of  and Interpretation of the Limit
and Interpretation of the Limit
The following examples show that the estimator ![]() based on the mis‐specified density
h ≠ f
generally converges to a value
θ
* ≠ θ
0
which can be interpreted in a reparameterised model.
based on the mis‐specified density
h ≠ f
generally converges to a value
θ
* ≠ θ
0
which can be interpreted in a reparameterised model.
9.2.3 Choice of Instrumental Density h
We have seen that, for any fixed
h
, there exists an identifiability constraint implying the convergence of ![]() to
θ
0
(see Table 9.3). In practice, we do not choose the parameterisation for which
to
θ
0
(see Table 9.3). In practice, we do not choose the parameterisation for which ![]() converges, but the estimator that guarantees a consistent estimation of the model of interest. The instrumental function
h
is chosen to estimate the model under a given constraint, corresponding to a given problem. As an example, suppose that we wish to estimate the conditional moment
converges, but the estimator that guarantees a consistent estimation of the model of interest. The instrumental function
h
is chosen to estimate the model under a given constraint, corresponding to a given problem. As an example, suppose that we wish to estimate the conditional moment ![]() of a GARCH (p, q) process. It will be convenient to consider the parameterisation ε
t
= σ
t
η
t
under the constraint
of a GARCH (p, q) process. It will be convenient to consider the parameterisation ε
t
= σ
t
η
t
under the constraint ![]() . The volatility
σ
t
will then be directly related to the conditional moment of interest, by the relation
. The volatility
σ
t
will then be directly related to the conditional moment of interest, by the relation ![]() . In this particular case, the Gaussian QMLE is inconsistent (because, in particular, the QMLE of
α
i
converges to
. In this particular case, the Gaussian QMLE is inconsistent (because, in particular, the QMLE of
α
i
converges to ![]() ). In view of (9.26), to find relevant instrumental functions
h
, one can solve
). In view of (9.26), to find relevant instrumental functions
h
, one can solve
since ![]() and
E{1 + h
′(x)/h(η
t
)η
t
} = 0. The densities that solve this differential equation are of the form
and
E{1 + h
′(x)/h(η
t
)η
t
} = 0. The densities that solve this differential equation are of the form
For λ = 1, we obtain the double Weibull, and for λ = 4 a generalised Gaussian, which is in accordance with the results given in Table 9.3.
For the more general problem of estimating conditional moments of ∣ε
t
∣ or log ∣ ε
t
∣, Table 9.4 gives the parameterisation (that is, the moment constraint on
η
t
) and the type of estimator (that is, the choice of
h
) for the solution to be only a function of the volatility
σ
t
(a solution which is thus independent of the distribution
f
of
η
t
). It is easy to see that for the instrumental function
h
of Table 9.4, the estimator ![]() depends only on
r
and not on
c
and
λ
. Indeed, taking the case
r > 0, up to some constant we have
depends only on
r
and not on
c
and
λ
. Indeed, taking the case
r > 0, up to some constant we have

Table 9.4 Choice of h as function of the prediction problem.
| Problem | Constraint | Solution | Instrumental density, h |
| E t − 1|ε t | r , r > 0 | E|η t | r = 1 |
|
c|x| λ − 1 exp(−λ|x| r /r), λ > 0 |
| E t − 1|ε t |−r | E|η t |−r = 1 |
|
c|x|−λ − 1 exp(−λ|x|−r /r) |
| E t − 1 log |ε t | | E log |η t | = 0 | log σ t |
|
which shows that ![]() does not depend on
c
and
λ
. In practice, one can thus choose the simplest constants in the instrumental function, for instance
c = λ = 1.
does not depend on
c
and
λ
. In practice, one can thus choose the simplest constants in the instrumental function, for instance
c = λ = 1.
9.2.4 Asymptotic Distribution of 
Using arguments similar to those of Section 7.4, a Taylor expansion shows that, under ( 9.25),

where

and

The ergodic theorem and the CLT for martingale increments (see Section A.2) then entail that

where

with g 1(x, σ) = ∂g(x, σ)/∂σ and g 2(x, σ) = ∂g 1(x, σ)/∂σ .
Table 9.5 completes Table 9.1. Using the previous examples, this table gives the ARE of the QMLE and Laplace QMLE with respect to the MLE, in the case where f follows the Student t distribution. The table does not allow us to obtain the ARE of the QMLE with respect to Laplace QMLE, because the noise η t has a different normalisation with the standard QMLE or the Laplace QMLE (in other words, the two estimators do not converge to the same parameter).
Table 9.5
Asymptotic relative efficiency of the MLE with respect to the QMLE and to the Laplace QMLE: ![]() and
and ![]() , where
φ
denotes the
, where
φ
denotes the ![]() density, and
density, and ![]() the Laplace density.
the Laplace density.
|
|
ν | ||||||||
| 5 | 6 | 7 | 8 | 9 | 10 | 20 | 30 | 100 | |
| MLE – QMLE | 2.5 | 1.667 | 1.4 | 1.273 | 1.2 | 1.154 | 1.033 | 1.014 | 1.001 |
| MLE – Laplace | 1.063 | 1.037 | 1.029 | 1.028 | 1.030 | 1.034 | 1.070 | 1.089 | 1.124 |
For the QMLE, the Student
t
density
f
ν
with
ν
degrees of freedom is normalised so that Eηt
2 = 1, that is, the density of
η
t
is ![]() . For the Laplace QMLE,
η
t
has the density
f(y) = E ∣ t
ν
∣ f
ν
(yE ∣ t
ν
∣), so that
E ∣ η
t
∣ = 1.
. For the Laplace QMLE,
η
t
has the density
f(y) = E ∣ t
ν
∣ f
ν
(yE ∣ t
ν
∣), so that
E ∣ η
t
∣ = 1.
9.3 Alternative Estimation Methods
The estimation methods presented in this section are less popular among practitioners than the QML and LS methods, but each has specific features of interest.
9.3.1 Weighted LSE for the ARMA Parameters
Consider the estimation of the ARMA part of the ARMA(P, Q)‐GARCH (p, q) model

where (η t ) is an iid(0,1) sequence and the coefficients ω 0 , α 0i and β 0j satisfy the usual positivity constraints. The orders P, Q, p , and q are assumed known. The parameter vector is
the true value of which is denoted by
ϑ
0
, and the parameter space Ψ ⊂ ℝ
P + Q + 1
. Given observations
X
1,…, X
n
and initial values, the sequence ![]() is defined recursively by (7.22). The weighted LSE is defined as a measurable solution of
is defined recursively by (7.22). The weighted LSE is defined as a measurable solution of

where the weights ω t are known positive measurable functions of X t − 1, X t − 2, …. One can take, for instance,

with E|X 1|2s < ∞ and s ∈ (0, 1). It can be shown that there exist constants K > 0 and ρ ∈ (0, 1) such that

This entails that

Thus

which implies a finite variance for the score vector ![]() . Ling (2005) deduces the asymptotic normality of
. Ling (2005) deduces the asymptotic normality of ![]() , even in the case
, even in the case ![]()
9.3.2 Self‐Weighted QMLE
Recall that, for the ARMA‐GARCH models, the asymptotic normality of the QMLE has been established under the condition ![]() (see Theorem 7.5). To obtain an asymptotically normal estimator of the parameter
(see Theorem 7.5). To obtain an asymptotically normal estimator of the parameter ![]() of the ARMA‐GARCH model (9.29) with weaker moment assumptions on the observed process, Ling (2007) proposed a self‐weighted QMLE of the form
of the ARMA‐GARCH model (9.29) with weaker moment assumptions on the observed process, Ling (2007) proposed a self‐weighted QMLE of the form

where ![]() , using standard notation. To understand the principle of this estimator, note that the minimised criterion converges to the limit criterion
l(ϕ) = E
ϕ
ω
t
ℓ
t
(ϕ) satisfying
, using standard notation. To understand the principle of this estimator, note that the minimised criterion converges to the limit criterion
l(ϕ) = E
ϕ
ω
t
ℓ
t
(ϕ) satisfying

The last expectation (when it exists) is null, because η t is centred and independent of the other variables. The inequality x − 1 ≥ log x entails that

Thus, under the usual identifiability conditions, we have
l(ϕ) ≥ l(ϕ
0), with equality if and only if
ϕ = ϕ
0
. Note that the orthogonality between
η
t
and the weights
ω
t
is essential. Ling (2007) showed the convergence and asymptotic normality of ![]() under the assumption
E|X
1|
s
< ∞ for some
s > 0.
under the assumption
E|X
1|
s
< ∞ for some
s > 0.
9.3.3 L p Estimators
The previous weighted estimator requires the assumption ![]() . Practitioners often claim that financial series admit few moments. A GARCH process with infinite variance is obtained either by taking large values of the parameters, or by taking an infinite variance for
η
t
. Indeed, for a GARCH(1, 1) process, each of the two sets of assumptions
. Practitioners often claim that financial series admit few moments. A GARCH process with infinite variance is obtained either by taking large values of the parameters, or by taking an infinite variance for
η
t
. Indeed, for a GARCH(1, 1) process, each of the two sets of assumptions
- (i)
 ,
, - (ii)

implies an infinite variance for ε
t
. Under (i), and strict stationarity, the asymptotic distribution of the QMLE is generally Gaussian (see Section 7.1.1), whereas the usual estimators have non‐standard asymptotic distributions under (ii) (see Berkes and Horváth 2003b; Hall and Yao 2003; Mikosch and Straumann 2002), which causes difficulties for inference. As an alternative to the QMLE, it is thus interesting to define estimators having an asymptotic normal distribution under (ii), or even in the more general situation where both
α
01 + β
01 > 1 and ![]() are allowed. A GARCH model is usually defined under the normalisation constraint
are allowed. A GARCH model is usually defined under the normalisation constraint ![]() . When the assumption that
. When the assumption that ![]() exists is relaxed, the GARCH coefficients can be identified by imposing, for instance, that the median of
exists is relaxed, the GARCH coefficients can be identified by imposing, for instance, that the median of ![]() is
τ = 1. In the framework of ARCH(q) models, Horváth and Liese (2004) consider
L
p
estimators, including the
L
1
estimator
is
τ = 1. In the framework of ARCH(q) models, Horváth and Liese (2004) consider
L
p
estimators, including the
L
1
estimator

where, for instance, ![]() . When
. When ![]() admits a density, continuous and positive around its median
τ = 1, the consistency and asymptotic normality of these estimators are shown in Horváth and Liese (2004), without any moment assumption. An alternative to
L
p
‐estimators, which only requires
admits a density, continuous and positive around its median
τ = 1, the consistency and asymptotic normality of these estimators are shown in Horváth and Liese (2004), without any moment assumption. An alternative to
L
p
‐estimators, which only requires ![]() and can be applied to ARMA‐GARCH, is the self‐weighted quasi‐maximum exponential likelihood estimator studied by Zhu and Ling (2011).
and can be applied to ARMA‐GARCH, is the self‐weighted quasi‐maximum exponential likelihood estimator studied by Zhu and Ling (2011).
9.3.4 Least Absolute Value Estimation
For ARCH and GARCH models, Peng and Yao (2003) studied several least absolute deviations estimators. An interesting specification is

With this estimator, it is convenient to define the GARCH parameters under the constraint that the median of ![]() is 1. A reparameterisation of the standard GARCH models is thus necessary. Consider, for instance, a GARCH(1, 1) with parameters
ω
,
α
1
and
β
1
, and a Gaussian noise
η
t
. Since the median of
is 1. A reparameterisation of the standard GARCH models is thus necessary. Consider, for instance, a GARCH(1, 1) with parameters
ω
,
α
1
and
β
1
, and a Gaussian noise
η
t
. Since the median of ![]() is
τ = 0.4549…, the median of the square of
is
τ = 0.4549…, the median of the square of ![]() is 1, and the model is rewritten as
is 1, and the model is rewritten as
It is interesting to note that the error terms ![]() are iid with median 0 when
θ = θ
0
. Intuitively, this is the reason why it is pointless to introduce weights in the sum (9.30). Under the moment assumption
are iid with median 0 when
θ = θ
0
. Intuitively, this is the reason why it is pointless to introduce weights in the sum (9.30). Under the moment assumption ![]() and some regularity assumptions, Peng and Yao (2003) show that there exists a local solution of ( 9.30) which is weakly consistent and asymptotically normal, with rate of convergence
n
1/2
. This convergence holds even when the distribution of the errors has a fat tail: only the moment condition
and some regularity assumptions, Peng and Yao (2003) show that there exists a local solution of ( 9.30) which is weakly consistent and asymptotically normal, with rate of convergence
n
1/2
. This convergence holds even when the distribution of the errors has a fat tail: only the moment condition ![]() is required.
is required.
9.3.5 Whittle Estimator
In Chapter 2, we have seen that, under the condition that the fourth‐order moments exist, the square of a GARCH(p, q) satisfies the ARMA(max(p, q), q) representation
where

The spectral density of ![]() is
is

Let ![]() be the empirical autocovariance of
be the empirical autocovariance of ![]() at lag
h
. At Fourier frequencies
λ
j
= 2πj/n ∈ (−π, π], the periodogram
at lag
h
. At Fourier frequencies
λ
j
= 2πj/n ∈ (−π, π], the periodogram

can be considered as a non‐parametric estimator of ![]() . Let
. Let

It can be shown that

with equality if and only if θ = θ 0 (see Proposition 10.8.1 in Brockwell and Davis 1991). In view of this inequality, it is natural to consider the so‐called Whittle estimator

For ARMA with iid innovations, the Whittle estimator has the same asymptotic behaviour as the QMLE and LSE (which coincide in that case). For GARCH models, the Whittle estimator still exhibits the same asymptotic behaviour as the LSE, but it is generally less accurate than the QMLE. Moreover, Giraitis and Robinson (2001), Mikosch and Straumann (2002), and Straumann (2005) have shown that the consistency requires the existence of ![]() , and that the asymptotic normality requires
, and that the asymptotic normality requires ![]() .
.
9.4 Bibliographical Notes
The central reference of Sections 9.1 and 9.2 is Berkes and Horváth (2004), who give precise conditions for the consistency and asymptotic normality of the estimators ![]() . Slightly different conditions implying consistency and asymptotic normality of the MLE can be found in Francq and Zakoïan (2006c). These results were extended to a general conditionally heteroskedastic model and used for prediction purposes by Francq and Zakoian (2013b). Additional results, in particular concerning the interesting situation where the density
f
of the iid noise is known up to a nuisance parameter, are available in Straumann (2005). Newey and Steigerwald (1997) show that, in general conditional heteroscedastic models, a suitable parameterisation allows to consistently estimate part of the volatility parameter by non‐Gaussian QML estimation. Fan, Qi, and Xiu (2014) and Francq, Lepage, and Zakoian (2011) propose multi‐steps consistent estimators of the GARCH volatility parameters based on non‐Gaussian QML estimators. The adaptative estimation of the GARCH models is studied in Drost and Klaassen (1997) and also in Engle and González‐Rivera (1991), Linton (1993), González‐Rivera and Drost (1999), and Ling and McAleer (2003b). Drost and Klaassen (1997), Drost, Klaassen and Werker (1997), Ling and McAleer (2003a), and Lee and Taniguchi (2005) give mild regularity conditions ensuring the LAN property of GARCH.
. Slightly different conditions implying consistency and asymptotic normality of the MLE can be found in Francq and Zakoïan (2006c). These results were extended to a general conditionally heteroskedastic model and used for prediction purposes by Francq and Zakoian (2013b). Additional results, in particular concerning the interesting situation where the density
f
of the iid noise is known up to a nuisance parameter, are available in Straumann (2005). Newey and Steigerwald (1997) show that, in general conditional heteroscedastic models, a suitable parameterisation allows to consistently estimate part of the volatility parameter by non‐Gaussian QML estimation. Fan, Qi, and Xiu (2014) and Francq, Lepage, and Zakoian (2011) propose multi‐steps consistent estimators of the GARCH volatility parameters based on non‐Gaussian QML estimators. The adaptative estimation of the GARCH models is studied in Drost and Klaassen (1997) and also in Engle and González‐Rivera (1991), Linton (1993), González‐Rivera and Drost (1999), and Ling and McAleer (2003b). Drost and Klaassen (1997), Drost, Klaassen and Werker (1997), Ling and McAleer (2003a), and Lee and Taniguchi (2005) give mild regularity conditions ensuring the LAN property of GARCH.
Several estimation methods for GARCH models have not been discussed here, among them Bayesian methods (see Geweke 1989), the generalised method of moments (see Rich, Raymond, and Butler 1991), variance targeting and robust methods (see Muler and Yohai 2008, Hill 2015). Rank‐based estimators for GARCH coefficients (except the intercept) were recently proposed by Andrews (2009). These estimators are shown to be asymptotically normal under assumptions which do not include the existence of a finite fourth moment for the iid noise.
9.5 Exercises
9.1 (The score of a scale parameter is centred)
Show that if f is a differentiable density such that ∫ ∣ x ∣ f(x)dx < ∞, then

Deduce that the score vector defined by ( 9.3) is centred.
-
9.2 (Covariance between the square and the score of the scale parameter) Show that if
f
is a differentiable density such that ∫|x|3
f(x)dx < ∞, then

-
9.3 (Intuition behind Le Cam's third lemma) Let
φ
θ
(x) = (2πσ
2)−1/2 exp(−(x − θ)2/2σ
2) be the
 density and let the log‐likelihood ratio
density and let the log‐likelihood ratio
Determine the distribution of

when
 , and then when
, and then when  .
. -
9.4 (Fisher information) For the parametrisation (9.11), verify that

-
9.5 (Condition for the consistency of the MLE) Let
η
be a random variable with density
f
such that
E|η|
r
< ∞ for some
r ≠ 0. Show that

-
9.6 (Case where the Laplace QMLE is optimal) Consider a GARCH model whose noise has the Γ(b, b) distribution with density

where b > 0. Show that the Laplace QMLE is optimal.
-
9.7 (Comparison of the MLE, QMLE and Laplace QMLE) Give a table similar to Table 9.5, but replace the Student
t
distribution
f
ν
by the double Γ(b, p) distribution

where b, p > 0.
-
9.8 (Asymptotic comparison of the estimators
 ) Compute the coefficient
) Compute the coefficient  defined by (9.28) for each of the instrumental densities
h
of Table 9.4. Compare the asymptotic behaviour of the estimators
defined by (9.28) for each of the instrumental densities
h
of Table 9.4. Compare the asymptotic behaviour of the estimators  .
. -
9.9 (Fisher information at a pseudo‐true value)
Consider a GARCH (p, q) model with parameter
- Give an example of an estimator which does not converge to
θ
0
, but which converges to a vector of the formwhere ϱ is a constant.
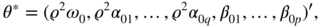
- What is the relationship between
 and
and  ?
? - Let Λϱ = diag(ϱ−2
I
q + 1, I
p
) and

Give an expression for J(θ *) as a function of J(θ 0) and Λϱ .
- Give an example of an estimator which does not converge to
θ
0
, but which converges to a vector of the form
-
9.10 (Asymptotic distribution of the Laplace QMLE) Determine the asymptotic distribution of the Laplace QMLE when the GARCH model does not satisfy the natural identifiability constraint
E ∣ η
t
∣ = 1, but the usual constraint
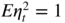 .
.
