In the previous chapter, there was an info box that introduced the concept of a tensor. That info box was a little simplified. If you google what a tensor is, you will get very conflicting results, which only serve to confuse. I don't want to add to the confusion. Instead, I shall only briefly touch on tensors in a way that will be relevant to our project, and in a way very much like how a typical textbook on Euclidean geometry introduces the concept of a point: by holding it to be self-evident from use cases.
Likewise, we will hold tensors to be self-evident from use. First, we will look at the concept of multiplication:
- First, let's define a vector:
. You can think of it as this diagram:
- Next, let's multiply the vector by a scalar value:
. The result is something like this:
There are two observations:
- The general direction of the arrow doesn't change.
- Only the length changes. In physics terms, this is called the magnitude. If the vector represents the distance travelled, you would have traveled twice the distance along the same direction.
So, how would you change directions by using multiplications alone? What do you have to multiply to change directions? Let's try the following matrix, which we will call T, for transformation:
Now if we multiply the transformation matrix with the vector, we get the following:
And if we plot out the starting vector and the ending vector, we get the resultant output:
As we can see, the direction has changed. The magnitude too has changed.
Now, you might be saying, hang on, isn't this just Linear Algebra 101?. Yes, it is. But to really understand a tensor, we must learn how to construct one. The matrix that we just used is also a tensor of rank-2. The proper name for a tensor of rank-2 is a dyad.
At around the same time as I was developing the earliest versions of Gorgonia, I was following a most excellent BBC TV series called Orphan Black, in which the Dyad Institute is the primary foe of the protagonists. They were quite villainous and that clearly left an impact in my mind. I decided against naming it thus. In retrospect, this seemed like a rather silly decision.
Now let's consider the transformation dyad. You can think of the dyad as a vector u times a vector v. To write it out in equation form:
At this point, you may be familiar with the previous chapter's notion of linear algebra. You might think to yourself: if two vectors multiply, that'd end up with a scalar value, no? If so, how would you multiply two vectors and get a matrix out of it?
Here, we'd need to introduce a new type of multiplication: the outer product (and by contrast, the multiplication introduced in the previous chapter is an inner product). We write outer products with this symbol: 
.
Specifically speaking, the outer product, also known as a dyad product, is defined as such:
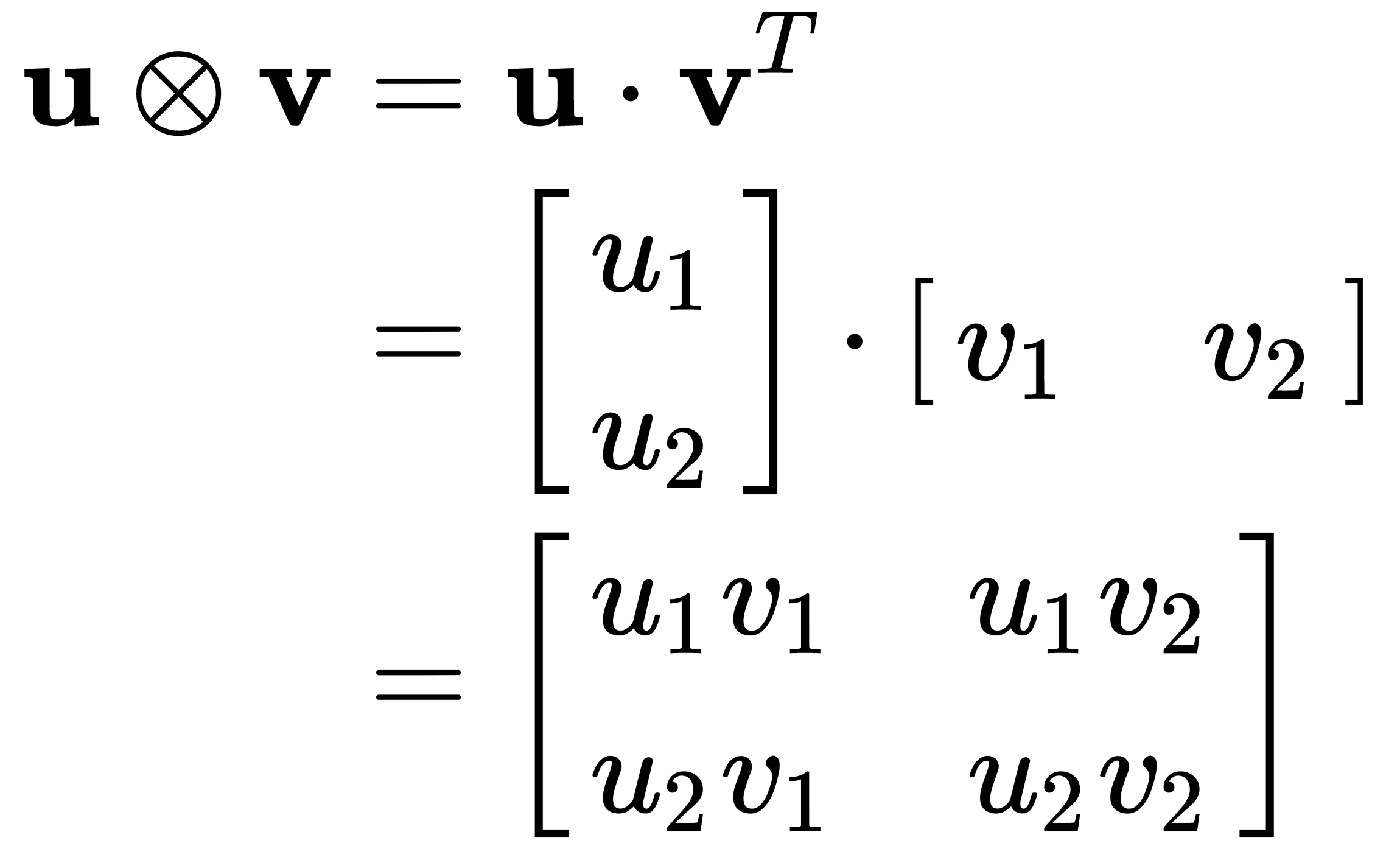
We won't be particularly interested in the specifics of u and v in this chapter. However, being able to construct a dyad from its constituent vectors is an integral part of what a tensor is all about.
Specifically, we can replace T with uv:
Now we get 
as the scalar magnitude change and u as the directional change.
So what is the big fuss with tensors? I can give two reasons.
Firstly, the idea that dyads can be formed from vectors generalizes upward. A three-tensor, or triad can be formed by a dyad product uvw, a four-tensor or a tetrad can be formed by a dyad product uvwx, and so on and so forth. This affords us a mental shortcut that will be very useful to us when we see shapes that are associated with tensors.
The useful mental model of what a tensor can be thought as is the following: a vector is like a list of things, a dyad is like a list of vectors, a triad is like a list of dyads, and so on and so forth. This is absolutely helpful when thinking of images, like those that we've seen in the previous chapter:
An image can be seen as a (28, 28) matrix. A list of ten images would have the shape (10, 28, 28). If we wanted to arrange the images in such a way that it's a list of lists of ten images, it'd have a shape of (10, 10, 28, 28).
All this comes with a caveat of course: a tensor can only be defined in the presence of transformation. As a physics professor once told me: that which transforms like a tensor is a tensor. A tensor devoid of any transformation is just an n-dimensional array of data. The data must transform, or flow from tensor to tensor in an equation. In this regards, I think that TensorFlow is a ridiculously well-named product.