Group Theory
10.1 Introduction
In this chapter, we will provide neither proofs nor detailed applications of group theory for either mathematics or scientific subjects. It will suffice to acquaint you with some of the motivation, terminology, and possible uses of this highly developed and widely applied branch of mathematics. Group theory deals with collections of entities which can be transformed among themselves by some appropriate operation. For example, the integers constitute a group (containing an infinite number of members) which can be transformed into one another by the operation of addition (which includes subtraction). Likewise, under the operation of multiplication, the four complex numbers ![]() can be recycled among themselves. Two versions of the Yin and Yang symbol (Figure 10.1) can be turned into one another by reversing the colors black and white or by rotating the figure by
can be recycled among themselves. Two versions of the Yin and Yang symbol (Figure 10.1) can be turned into one another by reversing the colors black and white or by rotating the figure by ![]() . Palindromes are words or phrases which read the same in either direction—like “RADAR” and Napoleon’s lament, “Able was I ere I saw Elba.” And, of course, everyone has marveled at the beautiful sixfold symmetry of snowflakes. Interpersonal behavior can develop symmetry, as in “tit for tat.” The algebraic expression
. Palindromes are words or phrases which read the same in either direction—like “RADAR” and Napoleon’s lament, “Able was I ere I saw Elba.” And, of course, everyone has marveled at the beautiful sixfold symmetry of snowflakes. Interpersonal behavior can develop symmetry, as in “tit for tat.” The algebraic expression ![]() is unchanged in value when x and y are interchanged. Likewise, the forms of Maxwell’s equations in free space (in the appropriate units) are preserved when the fields
is unchanged in value when x and y are interchanged. Likewise, the forms of Maxwell’s equations in free space (in the appropriate units) are preserved when the fields ![]() and
and ![]() are interchanged. Group-theoretical relationships are often revealed by patterns among the members of the collection. For example, in elementary particle theory, the systematic arrangement of masses, and spins of hadrons (particles subject to the strong interaction) eventually led to the quark model for baryons and mesons.
are interchanged. Group-theoretical relationships are often revealed by patterns among the members of the collection. For example, in elementary particle theory, the systematic arrangement of masses, and spins of hadrons (particles subject to the strong interaction) eventually led to the quark model for baryons and mesons.

Figure 10.1 Yin-Yang symbol and its color inverse. The original could then be retrieved by a 180° rotation. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this book.)
Symmetry in a technical sense implies that certain things remain invariant even when they are subject to some type of transformation. In fact, some of the fundamental laws of physics can be based on exact or approximate invariance of systems under certain real or abstract symmetry operations. In several important instances, an invariance or a symmetry implies a conservation law, a general principle known as Noether’s theorem. For example, the equations of mechanics appear to be invariant to an advance or retardation in the time variable. From this invariance, the conservation of energy can be deduced. Similarly, invariance with respect to translation and rotation in space implies conservation of linear and angular momentum, respectively. In quantum mechanics, the invariance of the Schrödinger equation with respect to a phase factor ![]() in the wavefunction
in the wavefunction ![]() implies the conservation of electric charge. More generally, localized invariance with respect to a phase factor
implies the conservation of electric charge. More generally, localized invariance with respect to a phase factor ![]() implies the existence of the quantized electromagnetic field. Such principles can be formalized as gauge field theories, which provide the basic structure of the Standard Model for electromagnetic, weak, and strong interactions.
implies the existence of the quantized electromagnetic field. Such principles can be formalized as gauge field theories, which provide the basic structure of the Standard Model for electromagnetic, weak, and strong interactions.
The strong nuclear force is insensitive to the distinction between neutrons and protons. These can be treated as alternative states of a single particle called a nucleon, differing in isotopic spin or isospin. It is found, for example, that the nuclei ![]() and
and ![]() have similar energy-level spectra. Isospin is, however, only an approximate symmetry. It is “broken” by electromagnetic interactions, since protons have electric charge while neutrons do not. Broken symmetry is a central theme in fundamental physics. An open question is how our Universe evolved to break the symmetry between matter and antimatter, so that it is now dominated by matter.
have similar energy-level spectra. Isospin is, however, only an approximate symmetry. It is “broken” by electromagnetic interactions, since protons have electric charge while neutrons do not. Broken symmetry is a central theme in fundamental physics. An open question is how our Universe evolved to break the symmetry between matter and antimatter, so that it is now dominated by matter.
10.2 Symmetry Operations
As a more concrete and elementary introduction to group theory, consider the symmetry operations which transform an equilateral triangle into an indistinguishable copy of itself. These are shown in Figure 10.2, with the vertices labeled as 1, 2, and 3. A group always contains an identity element, designated E, which represents the default operation of “doing nothing.” A positive (counterclockwise) rotation by an angle of ![]() is designated
is designated ![]() and the corresponding clockwise rotation is designated
and the corresponding clockwise rotation is designated ![]() . Reflections (or
. Reflections (or ![]() rotations) through the three vertices are designated
rotations) through the three vertices are designated ![]() , and
, and ![]() . These symmetry operations are represented in Figure 10.2 using colored triangles.
. These symmetry operations are represented in Figure 10.2 using colored triangles.
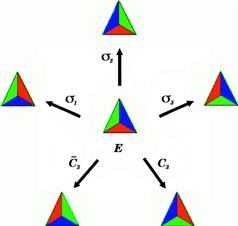
Figure 10.2 Symmetry operations on an equilateral triangle, shown with the aid of colored areas. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this book.)
The definitive property of a group is that successive application of two operations is equivalent to some single operation. For example,
![]() (10.1)
(10.1)
where the operation on the right is understood to be performed first. For the same two operations in reversed order, we find
![]() (10.2)
(10.2)
Thus, group elements do not, in general, commute
![]() (10.3)
(10.3)
although they may commute, as do ![]() and
and ![]() . (A group in which all products of elements commute is known as an Abelian group.) The algebra of the group can be summarized by the following
. (A group in which all products of elements commute is known as an Abelian group.) The algebra of the group can be summarized by the following ![]() group multiplication table:
group multiplication table:

Note that each operation appears exactly once, and only once, in each row and in each column. The group describing the symmetry operations on an equilateral triangle is designated in molecular theory as ![]() has precisely the same structure as the
has precisely the same structure as the ![]() possible permutations of three objects. The latter is known as the symmetric group of order 3, designated
possible permutations of three objects. The latter is known as the symmetric group of order 3, designated ![]() . These symmetry and permutation groups are said to be isomorphous—their abstract properties are identical although they apply to completely different sorts of objects.
. These symmetry and permutation groups are said to be isomorphous—their abstract properties are identical although they apply to completely different sorts of objects.
10.3 Mathematical Theory of Groups
A group is defined as a set of h abstract elements ![]() together with a rule for combination of these elements, which we usually refer to as a product. The mathematical properties of groups are entirely independent of any physical attributes that can be ascribed to their elements or rule of combination. For concreteness, however, we will usually apply the concepts of group theory to sets of geometrical symmetry operations. The elements of a group must fulfill the following four conditions:
together with a rule for combination of these elements, which we usually refer to as a product. The mathematical properties of groups are entirely independent of any physical attributes that can be ascribed to their elements or rule of combination. For concreteness, however, we will usually apply the concepts of group theory to sets of geometrical symmetry operations. The elements of a group must fulfill the following four conditions:
1. The product of any two elements of the group gives another element of the group. That is, ![]() with
with ![]() .
.
2. Group multiplication obeys an associative law, ![]() .
.
You can verify each of these conditions in the multiplication table for the group ![]() shown in the previous section. The number of elements h is called the order of the group. Thus,
shown in the previous section. The number of elements h is called the order of the group. Thus, ![]() is a group of order
is a group of order ![]() .
.
A subgroup is a smaller group selected from the elements of a given group, which itself fulfills all the properties of a group. For example, the set ![]() is itself a group of order 3. Likewise, each of the sets
is itself a group of order 3. Likewise, each of the sets ![]() for
for ![]() is a subgroup of order 2. Finally the identity element E is the trivial case of a subgroup of order 1. It can be proven that the order of any subgroup must be a divisor of the order of the group g.
is a subgroup of order 2. Finally the identity element E is the trivial case of a subgroup of order 1. It can be proven that the order of any subgroup must be a divisor of the order of the group g.
Every element of a group, say X, can be subjected to a set of similarity transformations using all the elements of the group, ![]() with
with ![]() , whereby
, whereby
![]() (10.4)
(10.4)
The element X, along with all the elements ![]() thus generated (there may be duplicates) are said to belong to the same class. The group
thus generated (there may be duplicates) are said to belong to the same class. The group ![]() has three classes:
has three classes: ![]()
![]() , and
, and ![]() . Evidently, for symmetry groups, the members of each class perform similar geometric operations, but oriented differently in space. The identity element, E, is always in a class by itself. The class structure of this group can be designated
. Evidently, for symmetry groups, the members of each class perform similar geometric operations, but oriented differently in space. The identity element, E, is always in a class by itself. The class structure of this group can be designated ![]() . Again, the number of members or each class must be a divisor of the order of the group g.
. Again, the number of members or each class must be a divisor of the order of the group g.
10.4 Representations of Groups
A set of quantities which obeys the group multiplication table is called a representation of the group. Because of the possible noncommutativity of group elements, simple numbers are not always adequate to represent groups; we must often use matrices. The group ![]() has three irreducible representations, or IRs, which cannot be broken down into simpler representations. A trivial, but nonetheless important, representation of every group is the totally symmetric representation, in which each group element is represented by 1. The multiplication table then simply reiterates that
has three irreducible representations, or IRs, which cannot be broken down into simpler representations. A trivial, but nonetheless important, representation of every group is the totally symmetric representation, in which each group element is represented by 1. The multiplication table then simply reiterates that ![]() . For
. For ![]() this is called the
this is called the ![]() representation:
representation:
![]() (10.5)
(10.5)
A slightly less trivial representation is ![]() :
:
![]() (10.6)
(10.6)
Much more exciting is the E representation, which requires ![]() matrices:
matrices:
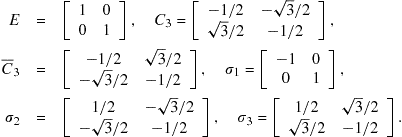 (10.7)
(10.7)
We can also find the following three-dimensional representation of the group, which we designate by ![]() :
:
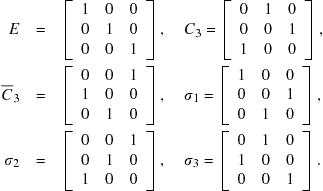 (10.8)
(10.8)
This is however a reducible representation of the group. By this we mean that there exists a similarity transformation, ![]() , which when applied to each of the matrices in (10.8) reduces them all to block diagonal form. For the
, which when applied to each of the matrices in (10.8) reduces them all to block diagonal form. For the ![]() representation, the matrix
representation, the matrix
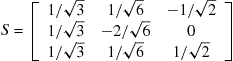 (10.9)
(10.9)
gives a reduction into a block diagonal form
 (10.10)
(10.10)
in which upper box stands for a one-dimensional representation, while the block of four boxes stands for a two-dimensional representation. In this case, these are, respectively, the ![]() and E representations. This reduction of the
and E representations. This reduction of the ![]() representation can be expressed symbolically as
representation can be expressed symbolically as
![]() (10.11)
(10.11)
A representation which cannot be further transformed into lower-dimensional representations is called an irreducible representation. We state without proof that the number of irreducible representations of a group is equal to the number of classes. Another important theorem states that the sum of the squares of the dimensionalities of the irreducible representations of a group adds up to the order of the group. Thus, for ![]() , we find
, we find ![]() . The general result is
. The general result is
![]() (10.12)
(10.12)
where ![]() is the dimension of the irreducible representation r.
is the dimension of the irreducible representation r.
We have usually referred to the operations of a group generically as multiplications. But, as mentioned earlier, addition can also be considered a group operation.
10.5 Group Characters
The trace or character of a matrix is defined as the sum of the elements along the main diagonal:
![]() (10.13)
(10.13)
For many purposes, it suffices to know just the characters of a matrix representation of a group, rather than the complete matrices. For example, the characters for the E representation of ![]() in Eq. (10.7) are given by
in Eq. (10.7) are given by
![]() (10.14)
(10.14)
Note that the characters for all operations in the same class are equal. Thus, the preceding equation can be abbreviated to
![]() (10.15)
(10.15)
For one-dimensional representations, such as ![]() and
and ![]() , the characters are equal to the matrices themselves, so Eqs. (10.5) and (10.6) can be directly read as character tables.
, the characters are equal to the matrices themselves, so Eqs. (10.5) and (10.6) can be directly read as character tables.
The characters of a group have an interesting orthonormality property:
![]() (10.16)
(10.16)
where the sum is over all the elements of the group, with r and s labeling two representations of the group. The last formula can, in fact, be derived from what is known as the Wonderful Orthogonality Theorem, which we state without proof:
![]() (10.17)
(10.17)
Here ![]() means the mnth matrix element of the representation r, with dimension
means the mnth matrix element of the representation r, with dimension ![]() , of the group element G.
, of the group element G.
For many purposes, particularly in applications to molecules, the essential information about a symmetry group is summarized in its character table. The character table for ![]() is shown here:
is shown here:

The last two columns show how the Cartesian coordinates ![]() , combinations of Cartesian coordinates and rotations
, combinations of Cartesian coordinates and rotations ![]() transform under the operations of the group. This is the only character table we will display explicitly. Character tables for all the relevant symmetry groups are given in many textbooks on group theory, quantum chemistry, and spectroscopy.
transform under the operations of the group. This is the only character table we will display explicitly. Character tables for all the relevant symmetry groups are given in many textbooks on group theory, quantum chemistry, and spectroscopy.
10.6 Group Theory in Quantum Mechanics
When a molecule belongs to the symmetry of a group ![]() , this means that each member of the group commutes with the molecular Hamiltonian
, this means that each member of the group commutes with the molecular Hamiltonian
![]() (10.18)
(10.18)
We now treat the group elements ![]() as operators on wavefunctions or orbitals
as operators on wavefunctions or orbitals ![]() , which are generally functions in three dimensions. Commuting operators can have simultaneous eigenfunctions. A representation of the group of dimension d means that there must exist a set of d degenerate eigenfunctions of H, which we designate by
, which are generally functions in three dimensions. Commuting operators can have simultaneous eigenfunctions. A representation of the group of dimension d means that there must exist a set of d degenerate eigenfunctions of H, which we designate by ![]() that transform among themselves in accord with the corresponding d-dimensional matrix representation of the group
that transform among themselves in accord with the corresponding d-dimensional matrix representation of the group ![]() . For example, if the eigenvalue
. For example, if the eigenvalue ![]() is d-fold degenerate, the vanishing commutators imply that, for
is d-fold degenerate, the vanishing commutators imply that, for
![]() (10.19)
(10.19)
Thus each ![]() is also an eigenfunction of H with the same eigenvalue
is also an eigenfunction of H with the same eigenvalue ![]() and must therefore be representable as a linear combination of the eigenfunctions
and must therefore be representable as a linear combination of the eigenfunctions ![]() More precisely, the eigenfunctions transform among themselves according to the relation
More precisely, the eigenfunctions transform among themselves according to the relation
![]() (10.20)
(10.20)
where ![]() means, in this case, the
means, in this case, the ![]() element of the matrix representing the operator
element of the matrix representing the operator ![]() . The character of the identity operation E immediately shows the degeneracy of the eigenvalues of that symmetry. The
. The character of the identity operation E immediately shows the degeneracy of the eigenvalues of that symmetry. The ![]() character table reveals that molecules of that same symmetry (for example, ammonia,
character table reveals that molecules of that same symmetry (for example, ammonia, ![]() ) can have only nondegenerate and twofold degenerate energy levels.
) can have only nondegenerate and twofold degenerate energy levels.
10.7 Molecular Symmetry Operations
Much information about molecules can be deduced from their symmetry group, even without quantum-mechanical computations. Specifically, we are dealing with point groups, so called because at least one point in the molecule remains fixed under all the symmetry operations of the group. Following is an enumeration of the types of symmetry operations that are needed to describe molecular configurations:
1. E: The identity transformation meaning do nothing (from the German Einheit, meaning unity.)
2. ![]() : Clockwise rotation by an angle of 2!/n radians (n is an integer). The axis for which n is maximum is called the principal axis.
: Clockwise rotation by an angle of 2!/n radians (n is an integer). The axis for which n is maximum is called the principal axis.
3. ![]() : Reflection through a plane (Spiegel is German for mirror).
: Reflection through a plane (Spiegel is German for mirror).
4. ![]() : Horizontal reflection plane, one passing through the origin and perpendicular to the principal axis.
: Horizontal reflection plane, one passing through the origin and perpendicular to the principal axis.
5. ![]() : Vertical reflection plane, one passing through the origin and containing the principal axis.
: Vertical reflection plane, one passing through the origin and containing the principal axis.
6. ![]() : Diagonal or dihedral reflection in a plane through the origin and containing the principal axis. Similar to
: Diagonal or dihedral reflection in a plane through the origin and containing the principal axis. Similar to ![]() except that it also bisects the angles between two
except that it also bisects the angles between two ![]() axes perpendicular to the principal axis.
axes perpendicular to the principal axis.
7. i: Inversion through the origin. In Cartesian coordinates, the transformation ![]() . Irreducible representations under this symmetry operation are classified as g (even) or u (odd).
. Irreducible representations under this symmetry operation are classified as g (even) or u (odd).
8. ![]() : An improper rotation or rotation-reflection axis. Clockwise rotation through an angle of 2!/n radians followed by a reflection in the plane perpendicular to the axis of rotation. Also known as an alternating axis of symmetry. Note that
: An improper rotation or rotation-reflection axis. Clockwise rotation through an angle of 2!/n radians followed by a reflection in the plane perpendicular to the axis of rotation. Also known as an alternating axis of symmetry. Note that ![]() is equivalent to
is equivalent to ![]() and
and ![]() is equivalent to i.
is equivalent to i.
Improper rotations can be visualized as shown in Figure 10.3.
Every molecule can be characterized as belonging to some group of symmetry operations from the above list, under which it can be transformed into indistinguishable copies of itself. We cannot, however, have arbitrary combinations of symmetry operations. For example, a molecule with a ![]() axis of rotation can only have mirror planes which either contain the axis or are perpendicular to it. We have been using the Schoenflies classification scheme, most favored by chemists. (Crystallographers generally use the International or Hermann-Mauguin classification).
axis of rotation can only have mirror planes which either contain the axis or are perpendicular to it. We have been using the Schoenflies classification scheme, most favored by chemists. (Crystallographers generally use the International or Hermann-Mauguin classification).
A symbol such as ![]() actually has a triple meaning in group theory. It can represent a symmetry element, namely an n-fold axis of rotation. It also designates the symmetry operation of rotation by
actually has a triple meaning in group theory. It can represent a symmetry element, namely an n-fold axis of rotation. It also designates the symmetry operation of rotation by ![]() radians about this axis. Finally, in the caligraphic form
radians about this axis. Finally, in the caligraphic form ![]() , it represents the symmetry group containing the elements
, it represents the symmetry group containing the elements ![]() .
.
Molecular structures illustrating the most important symmetry operations are given in the companion volume: S. M. Blinder, Introduction to Quantum Mechanics, Elsevier, 2004, pp. 206-212.

