Chapter One
Probability Space
1.1 Introduction/Purpose of the Chapter
The most important object when working with probability is the proper definition of the space studied. Typically, one wants to obtain answers about real-life phenomena which do not have a predetermined outcome. For example, when playing a complex game a person may be wondering: What are my chances to win this game? Or, am I paying too much to play this game, and is there perhaps a different game I should rather play? A certain civil engineer wants to know what is the probability that a particular construction material will fail under a lot of stress. To be able to answer these and other questions, we need to make the transition from reality to a space describing what may happen and to create consistent laws on that space. This framework allows the creation of a mathematical model of the random phenomena. This model, should it be created in the proper (consistent) way, will allow the modeler to provide approximate answers to the relevant questions asked. Thus, the first and the most important step in creating consistent models is to define a probability space which is capable of answering the interesting questions that may be asked.
We denote with Ω the set that contains all the possible outcomes of a random experiment. The set Ω is often called sample space or universal sample space. For example, if one rolls a die, Ω = {1, 2, 3, 4, 5, 6}. The space Ω does not necessarily contain numbers but rather some representation of the outcomes of the real phenomena. For example, if one looks at the types of bricks which may be used to build a house, a picture of each possible brick is a possible representation of each element of Ω.
A generic element of Ω will be denoted by ω. Any collection of outcomes (elements in Ω) is called an event. That is, an event is any subset of the sample space Ω. We will use capital letters from the beginning of the alphabet (A, B, C, etc.) to denote events.
In probability, one needs to measure the size of these events. Since an event is just a subset, we need to define those subsets of 3 Ω that can be measured. The concept of sigma algebra allows us to define a collection of subsets of the sample space on which a measure can be defined. In this chapter we introduce the notion of algebra and sigma algebra and we discuss their basic properties.
1.2 Vignette/Historical Notes
The first recorded notions of Probability Theory appear in 1654 in an exchange of letters between the famous mathematicians Blaise Pascal and Pierre de Fermat. The correspondence was prompted by a simple observation by Antoine Gombaud Chevalier de Méré, a French nobleman with an interest in gambling and who was puzzled by an apparent contradiction concerning a popular dice game. The game consisted of throwing a pair of dice 24 times; the problem was to decide whether or not to bet even money on the occurrence of at least one “double six” during the 24 throws. A seemingly well-established gambling rule led de Méré to believe that betting on a double six in 24 throws would be profitable (based on the payoff of the game). However, his own calculations based on many repetitions of the 24 throws indicated just the opposite. If we translate de Méré problem in todays language, he was trying to establish if the event has probability greater than 0.5. Today the confusion is easy to pinpoint to the proper definition of the probability space. For example, the convention at the time was that rolling a three (two and one showing on the dice) would be the same as rolling a two (a double one). Puzzled by this and other similar gambling problems, de Méré wrote to Pascal. The further correspondence between Fermat and Pascal is the first known documentation of the fundamental principles of the theory of probability.
The first formal treatment of probability theory was provided by Pierre-Simon, marquis de Laplace (1749–1827) in his Théorie Analytique des Probabilités published in 1812. (Laplace, 1886, republished). In 1933 the monograph Grundbegriffe der Wahrscheinlichkeitsrechnung by the Russian preeminent mathematician Andrey Nikolaevich Kolmogorov (1903–1987) outlined the axiomatic approach that forms the basis of the modern probability theory as we know it today (Kolmogoroff, 1973, republished).
1.3 Notations and Definitions
The following notations will be used throughout the book for set (event) operations. In the following, ω is any element and A, B are any sets in the sample space Ω.
- We describe a set or a collection of elements using a notation of the form
![]()
- ø is a notation for the set that does not contain any element. This set is called the empty set.
- ω
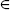 A denotes that the element ω is in the set A; we say “ω belongs to A.” Obviously, ω ∉ A means that the element is not in the set.
A denotes that the element ω is in the set A; we say “ω belongs to A.” Obviously, ω ∉ A means that the element is not in the set. - A ⊆ B denotes that A is a subset of B; that is, every element in A is also in B. The set A may actually be equal to B. In contrast, the notation A ⊂ B means that A is a proper subset of B; that is, A is strictly included in B. Mathematically, A ⊆ B is equivalent to the following statement: Any x
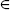 A implies x
A implies x 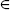 B.
B. - Union of sets:
![]()
- Intersection of sets:
![]()
- Complement of a set:
![]()
- Difference of two sets:
![]()
- Symmetric difference:
![]()
- Two sets A, B such that A∩ B = ø are called disjoint or mutually exclusive sets.
- A collection of sets A1, A2, …, An such that A1 ∪ A2 ∪ … ∪ An = Ω and Ai∩ Aj = ø for any i ≠ j is called a partition of the space Ω.
Every set operation may be expressed in terms of basic operations. For example,
![]()
There is a distributive law for intersection over union. If A, B, C are included in Ω, then
![]()
and
![]()
Furthermore, Ωc =ø and øc = Ω, and for all A ⊂ Ω we have
![]()
The De Morgan laws are also very important:
All of these rules may be extended to any finite number of sets in an obvious way. More details and further references about set operations may be found in Billingsley (1995) or Chung (2000).
1.4 Theory and Applications
1.4.1 Algebras
We introduce the notion of σ-algebra (or σ-field) to introduce a collection of sets which we may measure. In other words, we introduce a proper domain of definition for the (soon to be introduced) probability function. First let us denote
![]()
that is, ![]() is the collection of all possible subsets of Ω, a set containing all possible sets in Ω. This collection is called the parts of Ω.
is the collection of all possible subsets of Ω, a set containing all possible sets in Ω. This collection is called the parts of Ω.
An algebra on Ω is a collection of such sets in ![]() (including Ω) which is closed under complementarity and finite union.
(including Ω) which is closed under complementarity and finite union.
Let us list some immediate property of an algebra.
Proof: Note that these are properties of the collection of sets. The collection ![]() must contain these. Specifically, ø = Ωc and since Ω
must contain these. Specifically, ø = Ωc and since Ω ![]()
![]() the second point in Definition 1.1 says that ø
the second point in Definition 1.1 says that ø ![]()
![]() . Since
. Since
![]()
by the DeMorgan laws (1.1), points ii and iii in Definition 1.1 imply that (A ∩ B)c is in ![]() and so A ∩ B is in
and so A ∩ B is in ![]() . The proof for the third part is a simple induction on n ≥ 2, with the verification step already provided in iii of Definition 1.1.
. The proof for the third part is a simple induction on n ≥ 2, with the verification step already provided in iii of Definition 1.1. ![]()
1.4.2 Sigma Algebras
A σ-algebra on Ω is a generalization of an algebra on Ω.
Definition 1.3 implies other properties of a σ-algebra. For example, if a sigma algebra contains two elements A and B, it also contains A ∩ B and A ∪ B. The fact that the intersection must be in the σ-algebra is an easy consequence of point ii in the above definitions. For the σ-algebra case the intersection can be extended to a countable number of events as the next result shows.
Proof: Since ø = Ωc and ![]() , it follows that
, it follows that
![]()
For the second part, we note that
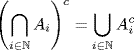
and since for every ![]() ,
, ![]() from the second part of the definition, their countable union is
from the second part of the definition, their countable union is ![]() , and thus its complement is
, and thus its complement is ![]() .
. ![]()
The σ-algebra is a very nice collection of sets. Using simple the operations union, intersection, complementarity, and difference applied to any sets in the σ-algebra, we end up with a set still in the σ-algebra. In fact, we may apply these simple operations in any combination a countably infinite number of times and we still end up with a set in the σ-algebra.
However, a noncountable intersection or union of the elements of a σ-algebra does not necessarily belongs to it (although it may). This can only happen when the index n is in some continuous set—for example, n ![]() (0, 1). Such situations are advanced: however, they become relevant when talking about stochastic processes. Extra care has to be observed in these cases. In the context of stochastic processes, we will introduce filtrations, which are simply increasing σ-algebras.
(0, 1). Such situations are advanced: however, they become relevant when talking about stochastic processes. Extra care has to be observed in these cases. In the context of stochastic processes, we will introduce filtrations, which are simply increasing σ-algebras.
Because of these nice properties, a σ-algebra provides a suitable domain of definition for the probability function (and thus defines probabilities of random events). However, a σ-algebra is a very abstract concept which, in general, is hard to work with. To simplify notions, we introduce the next definition. It will be much easier to work with the generators of a σ-algebra.
This will be a recurring theme in probability; in order to show a property for a big class, we show the property for a small generating subset of the class and then use standard arguments to extend the property to the entire class.
The idea, as mentioned earlier, is to verify some statement on the set ![]() . Then, due to the properties that would be presented later, the said statement will be extended and be valid for all the sets in σ(
. Then, due to the properties that would be presented later, the said statement will be extended and be valid for all the sets in σ(![]() ).
).
Proof: The proof is left as an exercise (see Exercise 1.12). ![]()
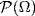 is a σ-algebra, the largest possible σ-algebra on Ω.
is a σ-algebra, the largest possible σ-algebra on Ω.- If the collection
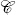 is already a σ-algebra, then σ(
is already a σ-algebra, then σ(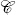 ) =
) = 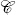 .
. - If
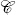 = {∅} or
= {∅} or 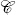 = {Ω}, then σ(
= {Ω}, then σ(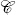 ) = {∅, Ω}, the smallest possible σ-algebra on Ω.
) = {∅, Ω}, the smallest possible σ-algebra on Ω. - If
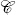 ⊆
⊆ 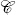 accprime, then σ(
accprime, then σ(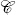 ) ⊆ σ(
) ⊆ σ(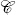 accprime).
accprime). - If
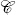 ⊆
⊆ 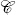 ' ⊆ σ(
' ⊆ σ(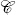 ), then σ(
), then σ(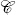 ') = σ(
') = σ(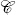 ).
).
Again, these properties are easy to derive directly from the definition and are left as exercise.
In general, listing all the elements of a σ-algebra explicitly is hard. Only in simple cases is this is even possible. This explains why we prefer to work with the generating collection ![]() instead of directly with the σ-algebra σ(
instead of directly with the σ-algebra σ(![]() ).
).
1.4.3 Measurable Spaces
After introducing σ-algebras, we are now able to give the notion of a space on which we can introduce probability measure.
On this type of space we shall introduce the probability measure.
1.4.4 Examples
Solution: A common mistake made by students who learn these notions is the following argument:
A ⊂ B; therefore, using the fourth property in the proposition above, we obtain σ(A) ⊆ σ(B) and therefore the σ-algebra asked is σ(A, B) = σ(B) = {Ω, ø, B, Bc}.
This argument is wrong on several levels. Firstly, the quoted property refers to collections of sets and not to the sets themselves. While it is true that A ⊂ B, it is not true that {A} ⊂ {B} as collections of sets. Instead, {A} ⊂ {A, B} and indeed this implies σ(A) ⊆ σ(A, B) (and similarly for σ(B)). But this just means that the result should contain all the sets in σ(A) (the sets in the previous example).
Second, as this example shows and as the following proposition says, it is not true that σ(A) ∪ σ(B) = σ(A, B), so we can't just simply list all the elements in σ(A) and σ(B) together. The only way to solve this problem is the hard way—that is, actually calculating the sets.
Clearly, σ(A, B) should contain the basic sets and their complements; thus
![]()
The σ-algebra should also contain all their unions according to the definition. Therefore, it must contain
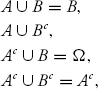
where the equalities are obtained using that A ⊂ B. So the only new set to be added is A ∪ Bc and thus its complement as well: (A ∪ Bc)c = Ac ∩ B. Now we need to verify that by taking unions we do not obtain any new sets, a task left for the reader. In conclusion, when A ⊂ B we have
![]()
![]()
Proof: For part 2 there is nothing to show. A counterexample is immediate from the previous exercise. Take ![]() and
and ![]() . Example 1.3 calculates σ(A, B), and it is simple to see that
. Example 1.3 calculates σ(A, B), and it is simple to see that ![]() needs more sets to become a σ-algebra. It is worth mentioning that in some trivial cases the union may be a σ-algebra, such as for example when
needs more sets to become a σ-algebra. It is worth mentioning that in some trivial cases the union may be a σ-algebra, such as for example when ![]() and they both contain a countable number of elements.
and they both contain a countable number of elements.
For part 1 we need to verify the three properties in the definition of the sigma algebra. For example, take A in ![]() . So A belongs to both collections of sets. Since
. So A belongs to both collections of sets. Since ![]() is a σ-algebra by definition, we have
is a σ-algebra by definition, we have ![]() . Similarly,
. Similarly, ![]() . Therefore,
. Therefore, ![]() . The rest of the definition is verified in a similar manner.
. The rest of the definition is verified in a similar manner. ![]()
1.4.5 The Borel σ-Algebra
Let Ω be a topological space (think geometry is defined in this space, and this assures us that the open subsets exist in this space).
In the special case when ![]() , we denote
, we denote ![]() , the Borel sets of
, the Borel sets of ![]() . This
. This ![]() is the most important σ-algebra. The reason is that most experiments on abstract spaces Ω may be made equivalent with experiments on
is the most important σ-algebra. The reason is that most experiments on abstract spaces Ω may be made equivalent with experiments on ![]() (as we shall see later when we talk about random variables). Thus, if we define a probability measure on
(as we shall see later when we talk about random variables). Thus, if we define a probability measure on ![]() , we have a way to calculate probabilities for most experiments.
, we have a way to calculate probabilities for most experiments.
There is nothing special about using the open sets as generators, except for the fact that the open sets can be defined in any topological space. The Borel sets over ![]() may be generated by various other classes of intervals; in the end the result is the same σ-algebra. Please see problem 2.10 for these classes of generators.
may be generated by various other classes of intervals; in the end the result is the same σ-algebra. Please see problem 2.10 for these classes of generators.
Pretty much, any subset of ![]() you can think about is in
you can think about is in ![]() . However, it is possible (though very difficult) to explicitly construct a subset of
. However, it is possible (though very difficult) to explicitly construct a subset of ![]() which is not in
which is not in ![]() . See (Billingsley, 1995, page 45) for such a construction in the case Ω = (0, 1]. These sets are generally constructed using a Cantor set argument.
. See (Billingsley, 1995, page 45) for such a construction in the case Ω = (0, 1]. These sets are generally constructed using a Cantor set argument.
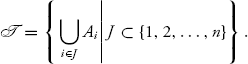
Solution: We start by proving that ![]() is a σ-algebra. First,
is a σ-algebra. First,
![]()
which implies that ![]() .
.
Suppose that ![]() is an element of
is an element of ![]() . Then its complement is
. Then its complement is
![]()
This is easy to see since Ai form a partition of Ω. Thus ![]() and the intersection of these gives exactly the sets not indexed by J. Therefore, Ac
and the intersection of these gives exactly the sets not indexed by J. Therefore, Ac ![]()
![]() .
.
Moreover, for any integer ![]() .
.
![]()
which implies that ![]() is closed under finite number of unions, and
is closed under finite number of unions, and ![]() is an algebra. Furthermore, since the total index set {1, 2, …, n} is finite, any countable union
is an algebra. Furthermore, since the total index set {1, 2, …, n} is finite, any countable union ![]() of subsets Jp is also included in {1, 2, …, n} and
of subsets Jp is also included in {1, 2, …, n} and ![]() is closed under countable unions, thus it is in fact a σ-algebra.
is closed under countable unions, thus it is in fact a σ-algebra.
Since ![]() is a σ-algebra which contains the events Ai, it must also contain the sigma algebra generated by A1, …, An. This means that
is a σ-algebra which contains the events Ai, it must also contain the sigma algebra generated by A1, …, An. This means that ![]() ⊇ σ(A1, …, An).
⊇ σ(A1, …, An).
Conversely, σ(A1, …, An) is a σ-algebra, thus by definition it must contain any countable (in particular finite) union of Ai's. But the set of finite unions is precisely ![]() , which shows that
, which shows that ![]() ⊆ σ(A1, …, An).
⊆ σ(A1, …, An).
The double inclusion above then shows that ![]() is the σ-algebra generated by A1, …, An.
is the σ-algebra generated by A1, …, An. ![]()
Solution: 1. We need to verify the three properties of a σ-algebra. Clearly ø ![]()
![]() , and by the definition of
, and by the definition of ![]() we have Ac
we have Ac ![]()
![]() if A
if A ![]()
![]() .
.
Let An be a sequence of events included in ![]() . We have two possibilities: Either all An's in the sequence are countable, or there exist an event in the sequence (An)n which is not countable.
. We have two possibilities: Either all An's in the sequence are countable, or there exist an event in the sequence (An)n which is not countable.
If every An is countable, then clearly
![]()
is countable (a countable union of countable sets is countable) and consequently ![]() nAn is in
nAn is in ![]() .
.
Suppose that there exists at least some set, say Ap, that is not countable. Since Ap ![]()
![]() , then
, then ![]() is countable. By DeMorgan laws (1.1) we have
is countable. By DeMorgan laws (1.1) we have
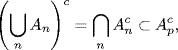
where the last inclusion holds because ![]() is countable. Thus, the complement of the set
is countable. Thus, the complement of the set ![]() is at most countable and therefore it belongs to
is at most countable and therefore it belongs to ![]() .
.
2. Clearly ![]() ⊆
⊆ ![]() . Recall that any finite set is also countable and so
. Recall that any finite set is also countable and so ![]() is a σ-algebra that contains all the finite parts of
is a σ-algebra that contains all the finite parts of ![]() . Since
. Since ![]() is the smallest σ-algebra that contains these finite parts, the inclusion follows.
is the smallest σ-algebra that contains these finite parts, the inclusion follows.
Conversely, we will prove that ![]() contains every set
contains every set ![]() such that A or Ac is finite or countable. Indeed, if A is countable, then A can be written as
such that A or Ac is finite or countable. Indeed, if A is countable, then A can be written as
![]()
Since every singleton {x} is in ![]() and
and ![]() is stable under countable union, we deduce that A
is stable under countable union, we deduce that A ![]()
![]() . If Ac is countable, the same argument applied to it will imply that Ac
. If Ac is countable, the same argument applied to it will imply that Ac ![]()
![]() . But
. But ![]() is a σ-algebra and so A
is a σ-algebra and so A ![]()
![]() . In either case we deduce that any set A in
. In either case we deduce that any set A in ![]() belongs to
belongs to ![]() . Therefore
. Therefore ![]() ⊆
⊆ ![]() , and by double inclusion the two are the same.
, and by double inclusion the two are the same.
3. The Borel σ-algebra contains all the finite subsets of ![]() . Therefore, we have
. Therefore, we have ![]() ⊂
⊂ ![]() . This inclusion is strict. Indeed, the interval (0, 1) is in
. This inclusion is strict. Indeed, the interval (0, 1) is in ![]() , but it is not in
, but it is not in ![]() because neither (0, 1) nor its complement is countable. Since
because neither (0, 1) nor its complement is countable. Since ![]() is the same as
is the same as ![]() , it is a proper subset (included strictly) of
, it is a proper subset (included strictly) of ![]() .
. ![]()
1.5 Summary
In this chapter we introduce the space on which probability is defined. This beginning chapter introduces the notion of σ-algebra, which is going to be the domain of definition for the probability measure. We need to know what we can measure and what we cannot. The sets that can be measured and given a probability will always be in the σ-algebra. Furthermore, this chapter introduces the basic notions of the set operations such as inclusion, intersection, and so on.
Exercises
1.1 Show that if A, B are two event in Ω, then
![]()
1.2 If (Ai)i![]() I is any collection of events in Ω, then show that
I is any collection of events in Ω, then show that
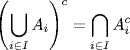
and
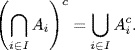
1.3 Roll a six-sided die. Use Ω = {1, 2, 3, 4, 5, 6} to denote the possible outcomes. An example of an event in this space Ω is A = {Roll an even number} = {2, 4, 6}. Find the cardinality (total number of elements) of ![]() .
.
1.4 Suppose two events A and B are in some space Ω. List the elements of the generated σ algebra σ(A, B) in the following cases:
1.5 An algebra which is not a σ-algebra
Let ![]() 0 be the collection of sets of the form (a1, a1'] ∪ (a2, a2'] ∪ … ∪ (am, am'], for any
0 be the collection of sets of the form (a1, a1'] ∪ (a2, a2'] ∪ … ∪ (am, am'], for any ![]() and all a1 < a1' < a2 < a2' < … < am < am' in Ω = (0, 1]. Verify that
and all a1 < a1' < a2 < a2' < … < am < am' in Ω = (0, 1]. Verify that ![]() 0 is an algebra. Show that
0 is an algebra. Show that ![]() 0 is not a σ-algebra.
0 is not a σ-algebra.
1.6 Let ![]() .
.
1.7 A σ-algebra does not necessarily contain all the events in Ω Let ![]() . Show that
. Show that ![]() is a σ-algebra.
is a σ-algebra.
Note that if Ω is uncountable, this implies that it contains a set A such that both A and Ac are uncountable, thus ![]() .
.
1.8 Show that the Borel sets of ![]() .
.
Hint: Show that the generating set is the same; that is, show that any set of the form (− ∞, x] can be written as countable union (or intersection) of open intervals and vice versa that any open interval in ![]() can be written as countable union (or intersection) of sets of the form (− ∞, x].
can be written as countable union (or intersection) of sets of the form (− ∞, x].
1.9 Show that the following classes all generate the Borel σ-algebra; or, expressed differently, show the equality of the following collections of sets:
![]()
where ![]() is the set of all rational numbers.
is the set of all rational numbers.
1.10 Let A, B, C be three events in a probability space. Express the following events in terms of elements in A, B, C using union, intersection, complementarity, etc.
1.11 Let ![]() ,
, ![]() be collections of subsets of Ω.
be collections of subsets of Ω.
1.12 Give a proof for Proposition 1.6.
Hint. Use exercise 1.11 for one of the two inclusions (the other one is obvious).
1.13 This problem gives the structure of the Borel σ-algebra on ![]() .
.
![]()
1.14 Prove the claim stated in Remark 1.11.
