Chapter Ten
Gaussian Random Vectors
10.1 Introduction/Purpose of the Chapter
Gaussian random variables and Gaussian random vectors (vectors whose components are jointly Gaussian, as defined in this chapter) play a central role in modeling real-life processes. Part of the reason for this is that noise like quantities encountered in many practical applications are reasonably modeled as Gaussian. Another reason is that Gaussian random variables and vectors turn out to be remarkably easy to work with (after an initial period of learning their features). Jointly Gaussian random variables are completely described by their means and covariances, which is part of the simplicity of working with them. Estimating these joint Gaussians means approximating only their means and covariances.
A third reason why Gaussian random variables and vectors are so important is that, in many cases, the performance measures we get for estimation and detection problems for the Gaussian case often bounds the performance for other random variables with the same means and covariances. For example, the minimum mean square estimator for Gaussian problems is the same as the linear least squares estimator for other problems with the same mean and covariance and, furthermore, has the same mean square performance. We will also find that this estimator has a simple expression as a linear function of the observations. Finally, we will find that the minimum mean square estimator for non-Gaussian problems always has a better performance than that for Gaussian problems with the same mean and covariance, but that the estimator is typically much more complex. The point of this example is that non-Gaussian problems are often more easily and more deeply understood if we first understand the corresponding Gaussian problem.
In this chapter, we develop the most important properties of Gaussian random variables and vectors, namely the moment-generating function, the moments, the joint densities, and the conditional probability densities.
10.2 Vignette/Historical Notes
The Gaussian distribution is named after Johann Carl Friedrich Gauss (30 April 1777–23 February 1855), one of the most famous mathematicians and physical scientists of the 18th century. Besides 301 probability and statistics, Gauss contributed significantly to many other fields, including number theory, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy, and optics.
Gauss work on a theory of the motion of planetoids disturbed by large planets, eventually published in 1809 as Theoria motus corporum coelestium in sectionibus conicis solem ambientum (Theory of motion of the celestial bodies moving in conic sections around the sun), contained an influential treatment of the method of least squares, a procedure which is used today in all sciences to minimize the impact of measurement error. Gauss proved the method under the assumption of normally distributed errors, a methodology that today is the first step in analysis of errors produced by very complex processes.
With the proper formulation of the Brownian motion (Wiener process) by Norbert Wiener in the 1950s the Gaussian process became mainstream for the theory of stochastic processes. The chaos theory developed in the 1970s owes a lot of gratitude to Gaussian processes to be able to produce useful formulas and bounds. Most of the machine learning theory uses assumptions about errors behaving like Gaussian processes. For all these reasons, learning about them is a crucial skill to be acquired by any aspiring student in probability.
10.3 Theory and Applications
10.3.1 The Basics
Let us first recall that a random variable follows the normal law N(μ, σ2) with σ > 0 if its density is given by
![]()
Before introducing the concept of Gaussian vector, let us list some properties of Gaussian random variables, which are already proven in the previous chapters of this book.
- The parameters μ and σ completely characterize the law of X.
- X ∼ N(μ, σ2) if and only if
![]()
- If X ∼ N(μ, σ2) and we denote μp = E(X − EX)p = E(X − μ)p, the p-central moment, then
![]()
![]()
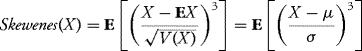
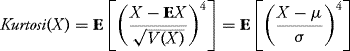
- If X ∼ N(μ, σ2), then
![]()
![]()
- The sum of two independent normal random variables is normal; that is, if
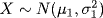 ,
, 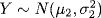 and X, Y are independent, then
and X, Y are independent, then
![]()
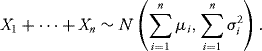
- The characteristic function of X ∼ N(μ, σ2) is
- The moment-generating function of X ∼ N(0, 1) is (see Proposition 9.16)
![]()
10.3.2 Equivalent Definitions of a Gaussian Vector
Let us now define the Gaussian vector.
The following two facts are immediate.
Proof: 1. Indeed, this follows from the definition by choosing αi = 1 and αj = 0 for every j ≠ i, j = 1, …, d.
2. It is a consequence of the definition of the Gaussian vector and of the Proposition 7.29. We mention that the assumption that Xi are independent is crucial. In this chapter, we will see examples showing that it is possible to have random vectors with each component Gaussian which are not Gaussian. ![]()
As we mention above, the mean and the variance characterize the law of a Gaussian random variable (one-dimensional). In the multidimensional case, the mean (which is a vector) and the covariance matrix will completely determine the law of a Gaussian vector.
Recall that if X = (X1, …, Xd) is a random vector, then
![]()
and the covariance matrix of X, denoted by ΛX = (ΛX(i, j))i,j=1,…,d, is defined by
![]()
for every i, j = 1, …, d.
Let us first remark that the mean and the covariance matrix of a Gaussian vector entirely characterize the first two moments (and thus the distribution) of every linear combination of the components of the vector. We recall the notation of a scalar product of two vectors:
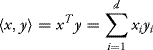
if ![]() , and we denoted by xT the transpose of the d × 1 matrix x.
, and we denoted by xT the transpose of the d × 1 matrix x.
Proof: It follows from Definition 10.1 that Y is a Gaussian r.v. (a linear combination of Gaussian random variables). It remains to compute its expectation and its variance. First
![]()
and
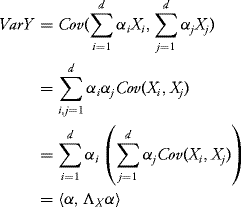
by noticing that the components of the vector ![]() are
are
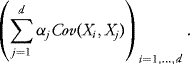
![]()
Using Proposition 10.4, it is possible to obtain the characteristic function of a Gaussian vector.
Proof: By definition, we have
![]()
Using Proposition 10.4, we have that, by Eq. (10.1),
![]()
where Y =![]() X, u
X, u ![]() . It suffices to note that
. It suffices to note that
![]()
for every ![]() .
. ![]()
Proof: Let ![]() and define
and define
![]()
For every ![]() we have
we have
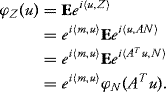
Suppose that X is a Gaussian vector. Since ΛX is symmetric and positive definite, there exists ![]() such that
such that
![]()
Let N1 ∼ N(0, Id). We apply Theorem 10.5 and the beginning of this proof. It follows that X and m + AN1 have the same characteristic function and therefore the same law. ![]()
The converse of Theorem 10.7 is also true.
Proof: Let
![]()
and consider the linear combination
![]()
where (AN)i is the component i of the vector ![]() , i = 1, …, d. Then, due to Proposition 10.4, we have
, i = 1, …, d. Then, due to Proposition 10.4, we have
![]()
So every linear combination of the components of X is a Gaussian random variable, which means that X is a Gaussian vector. ![]()
By putting together the results in Theorems 10.5, 10.7, and 10.8, we obtain three alternative characterization of a Gaussian vector.
Proof: The implication 1 ![]() 2 follows from Theorem 10.5. The implication 2
2 follows from Theorem 10.5. The implication 2 ![]() 3 is a consequence of the proof of Theorem 10.7. The implication 3
3 is a consequence of the proof of Theorem 10.7. The implication 3 ![]() 1 has been showed in Theorem 10.8.
1 has been showed in Theorem 10.8. ![]()
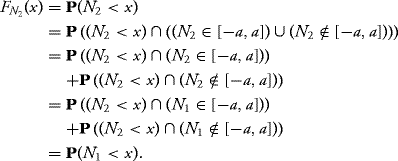
10.3.3 Uncorrelated Components and Independence
One of the most important properties of a Gaussian vector is the fact that its components are independent if and only if they are uncorrelated. One direction is always true for every random variable: If two random variables are independent, then they are uncorrelated. On the other hand, the converse is strongly related to the structure of the Gaussian vector, and it does not hold in general for other random variables. In Example 10.5 we show that that there exist Gaussian random variables (without the gaussian vector structure) which are uncorrelated but are not independent.
Proof: If Xi is independent by Xj, then clearly Cov(Xi, Xj) = 0, i ≠ j.
Suppose that Cov(Xi, Xj) = 0, i ≠ j. Denote by μ = EX and ΛX = (λi,j)i,j=1,…,d the mean vector and covariance matrix of the vector X. Since the individual covariances are zero, this matrix is a diagonal matrix and we have
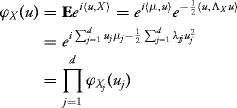
for every ![]() . We used the fact that for every j = 1, …, d, one has
. We used the fact that for every j = 1, …, d, one has
![]()
Since the characteristic function of the vector is the product of individual characteristic functions, the components of the vector X are independent. ![]()
Solution: Indeed, it is easy to see that (U, V) is a Gaussian vector (every linear combination of its components is a linear combination of X and Y and (X, Y) is a Gaussian vector). Moreover,
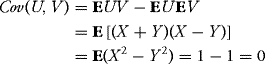
and the independence is obtained from Theorem 10.12. ![]()
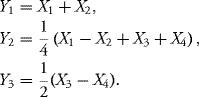
Solution: Let us first show that Y is a Gaussian vector. We note that
![]()
is a Gaussian vector with zero mean and covariance matrix I4. Take ![]() . Then
. Then
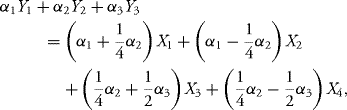
and this is a Gaussian r.v. since X is a Gaussian vector. Moreover,
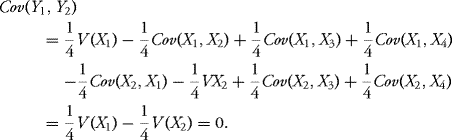
In the same way, we have
![]()
so Y1, Y2, Y3 are independent random variables. In fact, the vector Y is a Gaussian vector with EY = 0 and covariance matrix
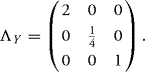
![]()
Solution: Since X − αY and Y are Gaussian random variables, it suffices to impose the condition
![]()
this implies
![]()
where we denoted with
![]()
the correlation coefficient between X and Y. ![]()
Solution: Let us show first that
![]()
Indeed, by computing the cumulative distribution function of Y, we get for every ![]()
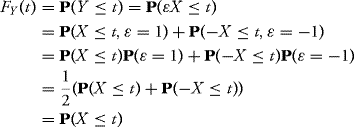
by using the fact that −X ∼ N(0, 1). So X, Y have the same law N(0, 1). Let us show that X, Y are uncorrelated. Indeed,
![]()
since Eε = 0. But it is easy to see that X and Y are not independent.
This example shows that it is possible to find two Gaussian uncorrelated r.v which are not independent. The reason why they are not independent is that the vector (X, Y) is not a Gaussian vector (see exercise 7.8). ![]()
A more general result can be stated as follows. The proof follows the arguments in the proof of Theorem 10.12.
10.3.4 The Density of a Gaussian Vector
Let X = (X1, …, Xd) be a Gaussian vector with independent components. Assume that for every i = 1, …, d we have
![]()
In this case it is easy to write the density of the vector X. It is, from Corollary 7.23,
In the case of a standard normal vector X ∼ N(0, Id), we have
![]()
When the components of X are not independent, we have the following.
Proof: From Theorem 10.7 we can write
![]()
where
![]()
We apply the change of variable formula (Theorem 7.24) to the function ![]() :
:
![]()
We have
![]()
We obtain
![]()
where fN denotes the density of the vector N ∼ N(0, Id). Since
![]()
and
![]()
we obtain the conclusion of the theorem. ![]()
However, in the case of degenerated Gaussian vectors, we have the property stated by the next proposition. We need to recall the notion of rank of a matrix. The rank of a matrix is the dimension of the vector space generated by its columns (or its rows). It is the largest possible dimension of a minor with determinant different from zero. A minor in a matrix can be constructed by eliminating any number of rows and columns. Obviously, if the d-dimensional matrix is invertible, then the rank of the matrix is d.
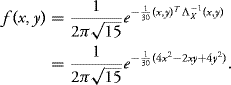
In the case of a Gaussian vector of dimension 2 (a Gaussian couple), we have the following:
Assume ρ2 ≠ 1. Then the density of the vector X is
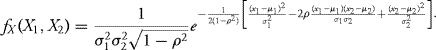
Proof: This follows from Theorem 10.4 since
![]()
![]()
10.3.5 Cochran's Theorem
Recall that if X ∼ N(0, 1), then ![]() , the gamma distribution with parameters
, the gamma distribution with parameters ![]() and
and ![]() . This law is called the chi square distribution and is usually denoted by χ2(1), with 1 denoting one degree of freedom. More generally, if X1, …, Xd are independent standard normal random variables, then
. This law is called the chi square distribution and is usually denoted by χ2(1), with 1 denoting one degree of freedom. More generally, if X1, …, Xd are independent standard normal random variables, then
![]()
follows the law ![]() and this is called the chi square distribution with d degrees of freedom, denoted by χ2(d).
and this is called the chi square distribution with d degrees of freedom, denoted by χ2(d).
This situation can be extended to nonstandard normal random variables.
Recall that the modulus (or the Euclidean norm) of a d-dimensional vector is
![]()
We can now state the Cochran theorem.
Proof: Let
![]()
be an orthonormal basis of Ej. Then
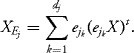
The random vectors ![]() are independent of distribution
are independent of distribution ![]() , so the random vectors
, so the random vectors ![]() are independent. To finish, it suffices to remark that
are independent. To finish, it suffices to remark that
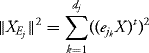
for every j = 1, …, d. ![]()
Let us give an important application of the Cochran's theorem to Gaussian random vectors.
Proof: We set for every i = 1, …, n
![]()
Then Yi are independent identically distributed N(0, 1). We also set
![]()
(by Vect(e) we mean the vector space of ![]() generated by the vector e). Then
generated by the vector e). Then
![]()
The projections of Y = (Y1, …, Yn) on E, E⊥ are independent and given by
![]()
and
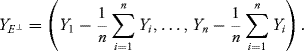
We therefore have
![]()
and
![]()
which gives the conclusion. ![]()
10.3.6 Matrix Diagonalization and Gaussian Vectors
We start with some notion concerning eigenvalues and eigenvectors of a matrix.
Proof: Let λ be an eigenvalue of A. If u ![]() Eλ is a corresponding eigenvector, then for every
Eλ is a corresponding eigenvector, then for every ![]() , α ≠ 0 we have
, α ≠ 0 we have
![]()
so
which shows that Eλ is closed under multiplication with scalars.
If ![]() is another vector in Eλ, then
is another vector in Eλ, then
![]()
so
Relations (10.6) and (10.7) show that Eλ is a vector space in ![]() .
. ![]()
Proof: If λ is an eigenvalue for A, there exists u ≠ 0, ![]() such that Au = λu; therefore
such that Au = λu; therefore
![]()
This implies that the matrix A − λIn is not invertible and thus det (A − λIn) = 0 .
Conversely, if det (A − λIn) = 0, then A − λIn is not invertible so there exists ![]() nonidentically zero such that (A − λIn)u = 0 .
nonidentically zero such that (A − λIn)u = 0 .
Finally, if λ is an eigenvalue of A, then the set of associated eigenvectors are the vectors ![]() satisfying (A − λIn)u = 0, which in fact is the definition of Ker(A − λIn).
satisfying (A − λIn)u = 0, which in fact is the definition of Ker(A − λIn). ![]()
In the case when A is diagonalizable, every column of the matrix P represents an eigenvector for A and the diagonal matrix D contains on its diagonal the eigenvalues of A. Each column i is an eigenvector for the eigenvalue i on the diagonal of D.
The following results apply to any random vector and not only the Gaussian random vectors. We shall review the requirement of a covariance matrix.
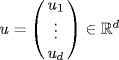 , u ≠ 0.
, u ≠ 0.Please note that uTAu is a number, thus its sign is unique. Further, we always consider vectors in ![]() as matrices having dimension d × 1.
as matrices having dimension d × 1.
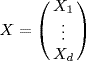 be a random vector with mean μ and covariance matrix ΛX. Then the matrix ΛX is symmetric and non-negative definite.
be a random vector with mean μ and covariance matrix ΛX. Then the matrix ΛX is symmetric and non-negative definite.Proof: To prove this proposition, let us first remark that the covariance matrix is a square matrix. Next, the element on row i column j is
![]()
thus the matrix must be symmetric.
About the positive definiteness for any 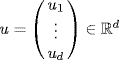 , we can construct the one-dimensional random variable: uTX. Since this is a valid random variable, its variance must be non-negative. So let us calculate this variance:
, we can construct the one-dimensional random variable: uTX. Since this is a valid random variable, its variance must be non-negative. So let us calculate this variance:
![]()
Since the number squared is one-dimensional, and a one-dimensional number is equal to its transpose, we may write
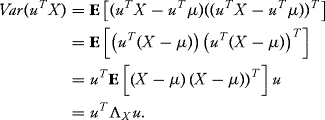
Thus, the condition that variance is non-negative translates into the condition that the covariance matrix is non-negative definite. ![]()
Checking that a square matrix is positive definite can be complicated. However, there is an easy way to check involving the eigenvalues of the matrix.
The following result is important because it can be applied to the covariance matrices.
The above result says that every symmetric positive definite matrix is diagonalizable in an orthonormal basis. That is, it can be transformed by elementary transformations into a diagonal matrix.
Proof: The proof follows by using Theorem 10.3.36. Since ΛX is a symmetric matrix, it can be diagonalizable in an orthonormal basis. That is, there exists an orthogonal matrix B such that BΛXBT is diagonal. The covariance of BX is BΛXBT, so the components of BX are independent Gaussian random variables. ![]()
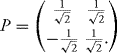
Exercises
Problems with Solution
10.1 Suppose
![]()
and define
![]()
Solution: Y is clearly a Gaussian vector since Y = AX with
![]()
where each component of Y is a linear combination of the original independent components Gaussian vector. To have the components of Y independent we need to impose the condition
![]()
But
![]()
Therefore if a + b = 0, the components Y1, Y2 are independent. Since
![]()
we will have in this case (a + b = 0)
![]()
![]()
10.2 Let X = (X1, X2, X3) be a random vector in ![]() with density
with density
![]()
![]()
Solution: Note that
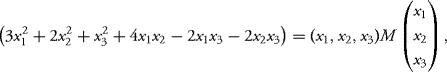
where
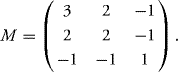
To see this decomposition, please think about how the polynomial terms appear. It helps to note that the diagonal elements give the squares in a unique way and thus they are easy to recognize. For the off diagonal elements note that twice the element gives the coefficient (because the matrix is symmetric).
Once we write it in this form, we recognize the density of aGaussian vector X with zero mean and covariance matrix
![]()
Consequently,
![]()
To solve part (b), we need to impose that
![]()
and
![]()
To impose these conditions, we need to calculate the covariance matrix:
![]()
Thus we need to know how to invert a matrix or to use a software program to do so. Using R gives
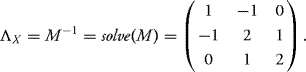
The command “solve(M)” is the R command to find the inverse of the matrix M. We can now read the covariances between the original vector components X1, X2, X3.
Now, using the matrix above and the formulas for the vector, the conditions are
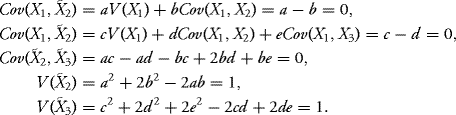
V (X1) is already 1. Using a = b and c = d from the first two equations, the later equations become
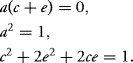
The first two equations are incompatible with a = 0, so we must have c = −e and either a = 1 or a = −1. Using this in the last equation gives e = 1. Thus the problem has more than one solution. Either of these vectors
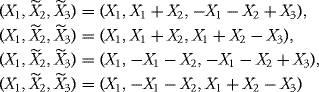
will have the desired properties.
Finally, for part (c), since either one of these vectors is Gaussian by requiring that the covariance matrix is the identity, we found components which are mutually independent. ![]()
10.3 Let X, X, Z be independent standard normal random variables. Denote
![]()
and
(10.8) ![]()
Show that U and V are independent.
Solution: Define
![]()
Clearly, A is a Gaussian vector with ![]() and covariance matrix
and covariance matrix
![]()
the identity matrix. It follows that the vector
![]()
is also a Gaussian vector (every linear combination of its components is a linear combination of X, Y, Z). We will show that the first component is independent of all the other three. To prove this since the vector is Gaussian, it suffices to show that the first component is uncorrelated with the other three. We have
![]()
and in a similar way
![]()
Therefore the r.v. X + Y + Z is independent of X − Y, X − Z, and Y − Z respectively. By the associativity property of the independence, we have that X + Y + Z is independent of (X − Y, X − Z, Y − Z) and, thus, independent of V. ![]()
10.4 Let X1, …, Xn be independent N(0, 1) distributed random variables. Let ![]() . Give a necessary and sufficient condition on the vector a in order to have X −
. Give a necessary and sufficient condition on the vector a in order to have X − ![]() a, X
a, X ![]() a and
a and ![]() a, X
a, X![]() independent.
independent.
Solution: The vector
![]()
is an (n + 1)-dimensional Gaussian vector and for every i = 1, …, n we obtain
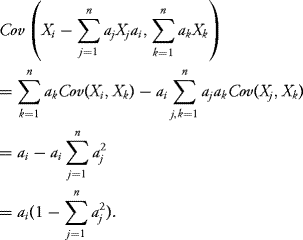
Therefore if we impose the condition
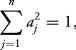
then all covariances between ![]() a, X
a, X![]() and the other terms of the vector will be zero. This will accomplish what is needed in the problem.
and the other terms of the vector will be zero. This will accomplish what is needed in the problem. ![]()
10.5 Let X = (X1, X2, …, Xn) denote an n-dimensional random vector with independent components such that ![]() for every i = 1, …, n. Define
for every i = 1, …, n. Define
![]()
Solution: As a sum of independent normal random variables, ![]() is a normal random variable. Its parameters can be easily calculated as mean
is a normal random variable. Its parameters can be easily calculated as mean ![]() and variance
and variance ![]() . So
. So
![]()
Note that the vector
![]()
is a Gaussian random vector. Indeed, every linear combination of its components is a linear combination of the components of X, so it is a Gaussian random variable. Therefore, ![]() and
and ![]() are independent if and only if they are uncorrelated; and after calculating the covariance, this is equivalent to
are independent if and only if they are uncorrelated; and after calculating the covariance, this is equivalent to
![]()
Hint for part (c): Wn is invariant by translation: Wn(X) = Wn(X + a) if X + a = (X1 + a, . . ., Xn + a) for ![]() . Consider also Proposition 10.24.
. Consider also Proposition 10.24. ![]()
10.6 Let (X, Y) be a Gaussian vector with mean 0 and covariance matrix
![]()
with ρ ![]() [− 1, 1]. What can be said about the random variables
[− 1, 1]. What can be said about the random variables
![]()
Solution: Clearly, (X, Z) is a Gaussian vector as a linear transformation of a Gaussian vector. Since
![]()
we note that the r.v.'s X and Z are independent. ![]()
10.7 Suppose X ∼ N(0, 1). Prove that for every x > 0 the following inequalities hold:
![]()
Solution: Consider the following functions defined on (0, ∞):
![]()
and
![]()
We need to show that
![]()
for every x > 0, where F is the c.d.f. of an N(0, 1) distributed random variable.
Since the normal c.d.f. does not have a closed form, we look at the derivatives of these functions. We need to check that for x > 0:
![]()
where ![]() is the standard normal density. Therefore, integrating the respective positive functions on (0, ∞), we obtain
is the standard normal density. Therefore, integrating the respective positive functions on (0, ∞), we obtain
![]()
and
![]()
![]()
Problems without Solution
10.8 Suppose
![]()
Show that XY has the same law as ![]()
Hint: Use the polarization formula
![]()
10.9 Prove the expression of the density function of the noncentral chi square distribution (10.5).
10.10 Let (X, Y) be a two-dimensional Gaussian vector with zero expectation and I2 covariance matrix. Compute
![]()
10.11 Let X, Y be two independent N(0, 1) distributed random variables. Define
![]()
![]()
10.12 Let X1, …, Xn be i.i.d. N(0, 1) random variables. Define
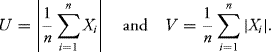
Compare and calculate EU and EV.
10.13 Let ![]() with
with
![]()
![]()
![]()
![]()
10.14 Suppose X ∼ N(0, Λ) where
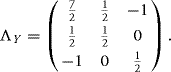
Let
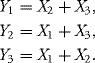
![]()
10.15 Let X = (X1, X2, X3) be a Gaussian vector with law N3(m, C) with density
![]()
where
![]()
![]()
10.16 Let (X, Y) be a normal random vector such that X and Y are standard normal N(0, 1). Suppose that Cov(X, Y) = ρ. Let ![]() and put
and put
![]()
10.17 Let (X, Y, Z) be a Gaussian vector with mean (1, 2, 3) and covariance matrix
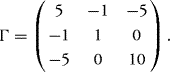
Set
![]()
10.18 If X is a standard normal random variable N(0, 1), let ϕ denote its characteristic function and F its c.d.f. For every p ≥ 1 integer, denote the p moment with
![]()
Let (Yn , n ≥ 1) be a sequence of independent r.v. with identical distribution N(0, 1). For every k ≥ 1 and n ≥ 1 integers, let
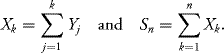
![]()
![]()
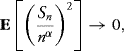
![]()
![]()
10.19 Let X1, X2, and X3 be three i.i.d. random variables where their distribution has zero mean and variance σ2 > 0. Denote
![]()
![]()
![]()
10.20 If X ∼ N(0, 1) and Y ∼ χ2(n, 1) and X, Y are independent, show that
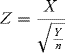
has a Student t distribution (tn) with n degrees of freedom. Specifically, show that the probability density function of Z is given by
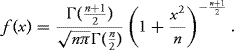
10.21 Assume X and Y are two independent N(0, 1) random variables. Find the law of
![]()
Hint: We know (how to prove) that X + Y and X − Y are independent and each has N(0, 2) distribution. Then, once we show that
![]()
is χ2(1) distributed, we will obtain
![]()
which follows a Student distribution with one degree of freedom (see exercise 20).
10.22 Consider the matrix
![]()
10.23 Consider the matrix
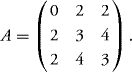
10.24 Let the matrix Σ be defined as
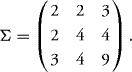
Check that the matrix is symmetric and positive definite. Find its eigenvalues and the associated eigenvectors. Now, let X be a Gaussian random vector with covariance matrix Σ and zero mean. Find a linear transformation that transforms X in a Gaussian vector with independent components.
