Principal component analysis (PCA) is one of the most intuitively simple and frequently used methods for applying dimension reduction to data and projecting it onto an orthogonal subspace of features. In a very general form, it can be represented as the assumption that all our observations look like some ellipsoid in the subspace of our original space. Our new basis in this space coincides with the axes of this ellipsoid. This assumption allows us to get rid of strongly correlated features simultaneously since the basis vectors of the space we project them onto are orthogonal.

The dimension of this ellipsoid is equal to the dimension of the original space, but our assumption that the data lies in a subspace of a smaller dimension allows us to discard the other subspaces in the new projection; namely, the subspace with the least extension of the ellipsoid. We can do this greedily, choosing a new element one by one on the basis of our new subspace, and then taking the axis of the ellipsoid with maximum dispersion successively from the remaining dimensions.

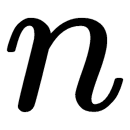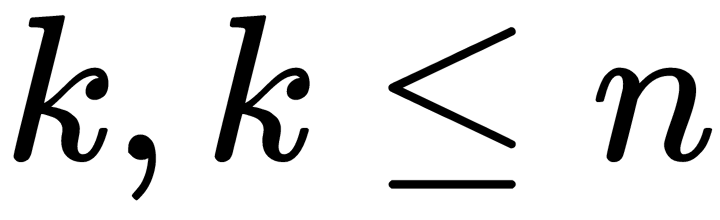To reduce the dimension of our data from  to , we need to choose the top  axes of such an ellipsoid, sorted in descending order by dispersion along the axes. To begin with, we calculate the variances and covariances of the original features. This is done by using a covariance matrix. By the definition of covariance, for two signs, 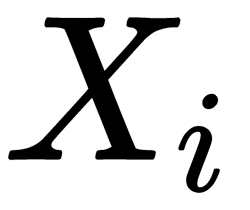 and 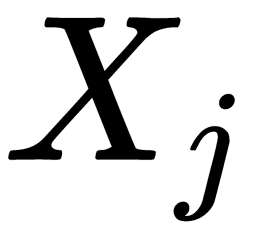, their covariance should be as follows:

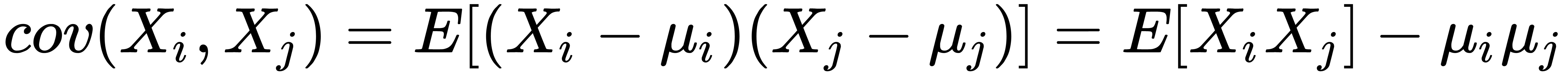
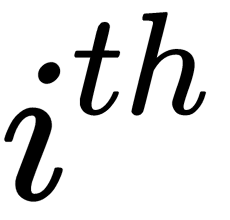Here,  is the mean of the  feature.

In this case, we note that the covariance is symmetric and that the covariance of the vector itself is equal to its dispersion. Thus, the covariance matrix is a symmetric matrix where the dispersions of the corresponding features lie on the diagonal and the covariances of the corresponding pairs of features lie outside the diagonal. In the matrix view, where 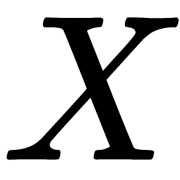is the observation matrix, our covariance matrix looks like this:

The covariance matrix is a generalization of variance in the case of multidimensional random variables – it also describes the shape (spread) of a random variable, as does the variance. Matrices such as linear operators have eigenvalues and eigenvectors. They are interesting because when we act on the corresponding linear space or transform it with our matrix, the eigenvectors remain in place, and they are only multiplied by the corresponding eigenvalues. This means they define a subspace that remains in place or goes into itself when we apply a linear operator matrix to it. Formally, an eigenvector, 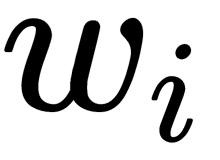_, with an eigenvalue for a matrix is defined simply as .

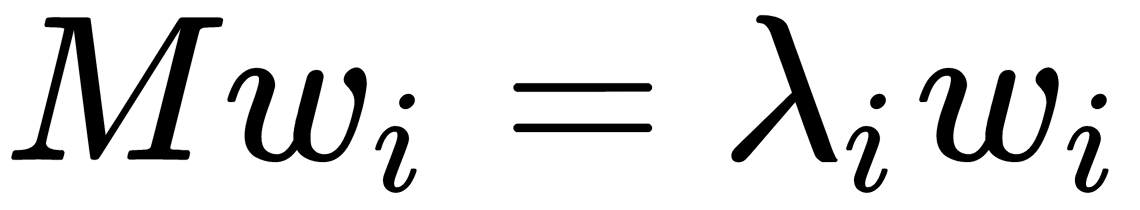The covariance matrix for our sample, _, can be represented as a product, 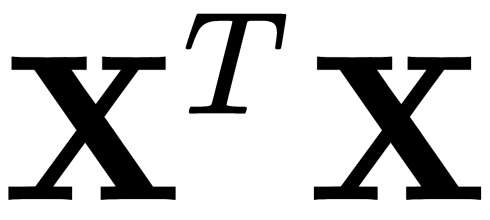. From the Rayleigh relation, it follows that the maximum variation of our dataset can be achieved along the eigenvector of this matrix, which corresponds to the maximum eigenvalue. This is also true for projections on a higher number of dimensions – the variance (covariance matrix) of the projection onto the m-dimensional space is maximum in the direction of  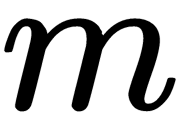eigenvectors with maximum eigenvalues. Thus, the principal components that we would like to project our data for are simply the eigenvectors of the corresponding top k pieces of the eigenvalues of this matrix.

The largest vector has a direction similar to the regression line, and by projecting our sample onto it, we lose information, similar to the sum of the residual members of the regression. It is necessary to make the operation, 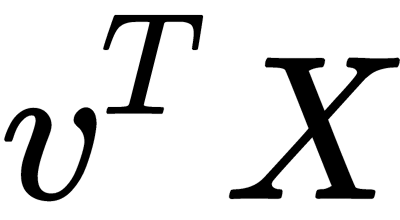 (the vector length (magnitude) should be equal to one), perform the projection. If we don't have a single vector and have a hyperplane instead, then instead of the vector, 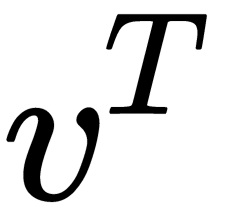, we take the matrix of basis vectors, 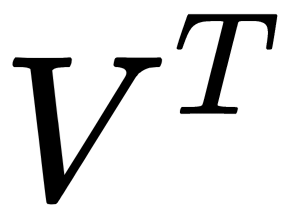. The resulting vector (or matrix) is an array of projections of our observations; that is, we need to multiply our data matrix on the basis vectors matrix, and we get the projection of our data orthogonally. Now, if we multiply the transpose of our data matrix and the matrix of the principal component vectors, we restore the original sample in the space where we projected it onto the basis of the principal components. If the number of components was less than the dimension of the original space, we lose some information.