The independent component analysis (ICA) method was proposed as a way to solve the problem of blind signal separation (BSS); that is, selecting independent signals from mixed data. Let's look at an example of the task of BSS. Suppose we have two people in the same room who are talking, generating acoustic waves. We have two microphones in different parts of the room, recording sound. The analysis system receives two signals from the two microphones, each of which is a digitized mixture of two acoustic waves – one from people speaking and one from some other noise (for example, playing music). Our goal is to select our initial signals from the incoming mixtures. Mathematically, the problem can be described as follows. We represent the incoming mixture in the form of a linear combination, where  represents the displacement coefficients and  represents the values of the vector of independent components:

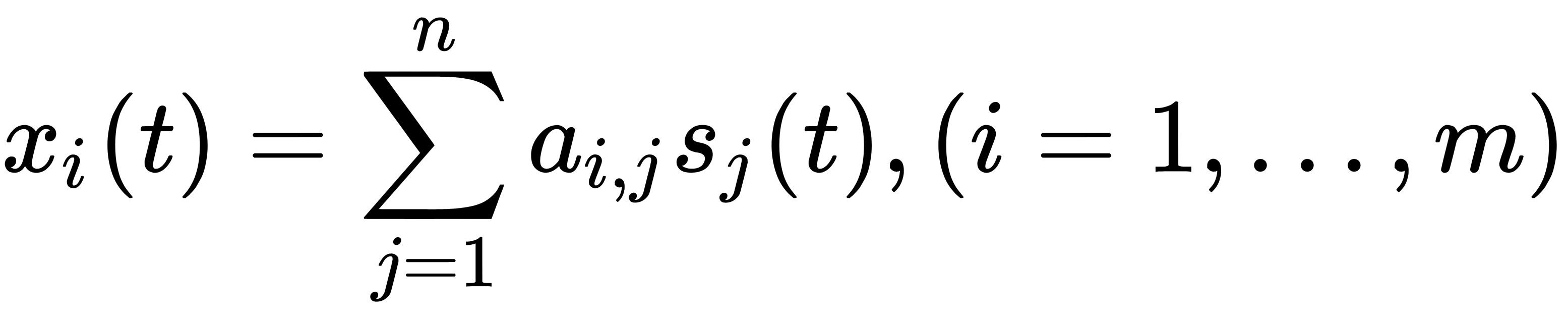
In matrix form, this can be expressed as follows:

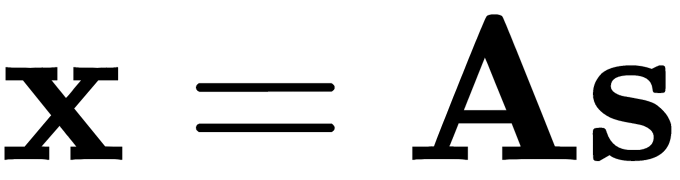
Here, we have to find the following:

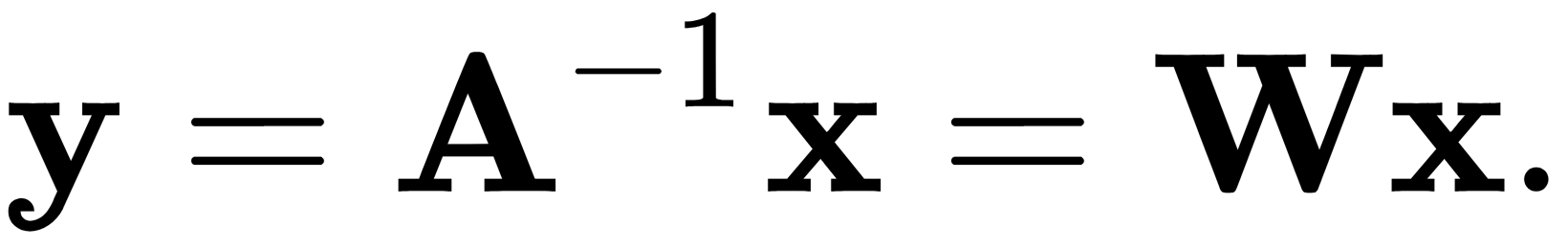
In this equation, 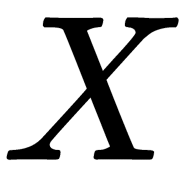 is a matrix of input signal values,  is a matrix of displacement coefficients or mixing matrix, and 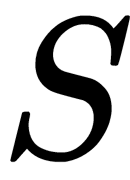 is a matrix of independent components. Thus, the problem is divided into two. The first part is to get the estimate, 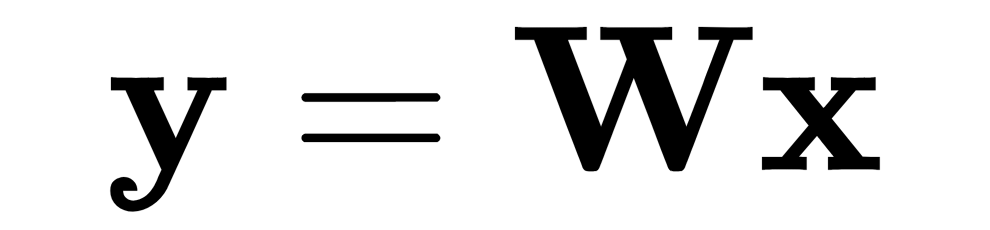, of the variables,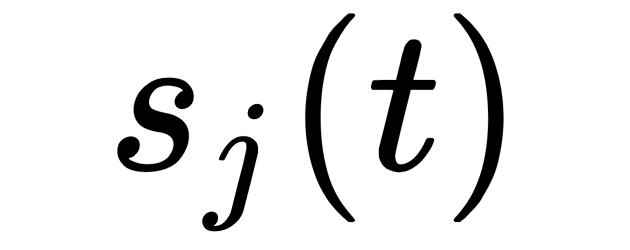, of the original independent components. The second part is to find the matrix,. How this method works is based on two principles:

• Independent components must be statistically independent ( 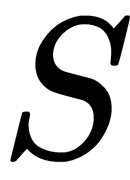matrix values). Roughly speaking, the values of one vector of an independent component do not affect the values of another component.
• Independent components must have a non-Gaussian distribution.

The theoretical basis of ICA is the central limit theorem, which states that the distribution of the sum (average or linear combination) of  independent random variables approaches Gaussian for 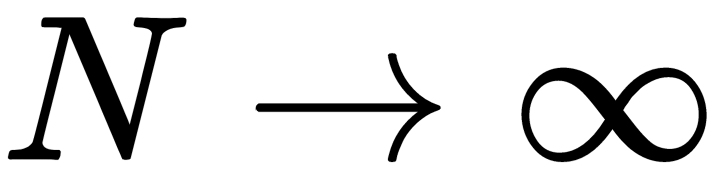. In particular, if  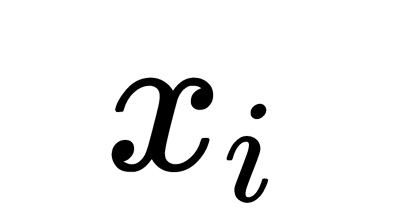are random variables independent of each other, taken from an arbitrary distribution with an average, 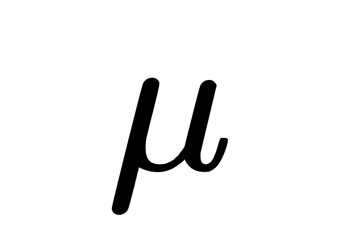,and a variance of 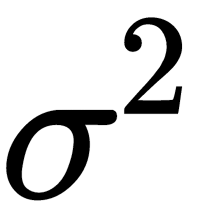, then if we denote the mean of these variables as 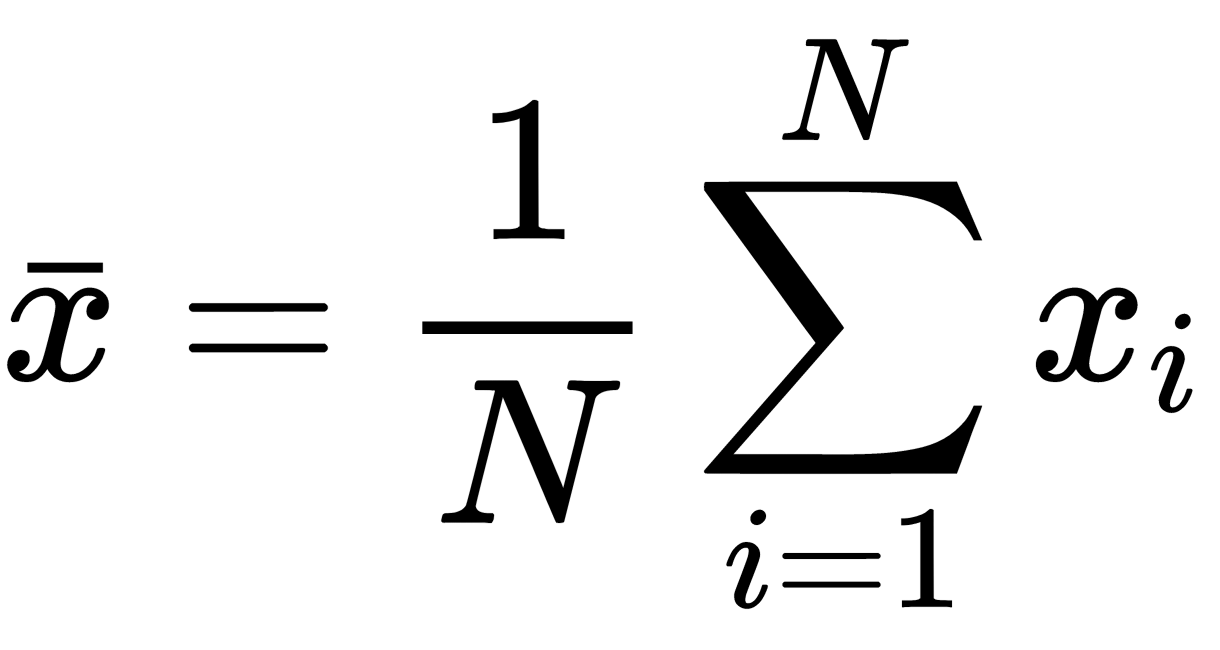, we can say that 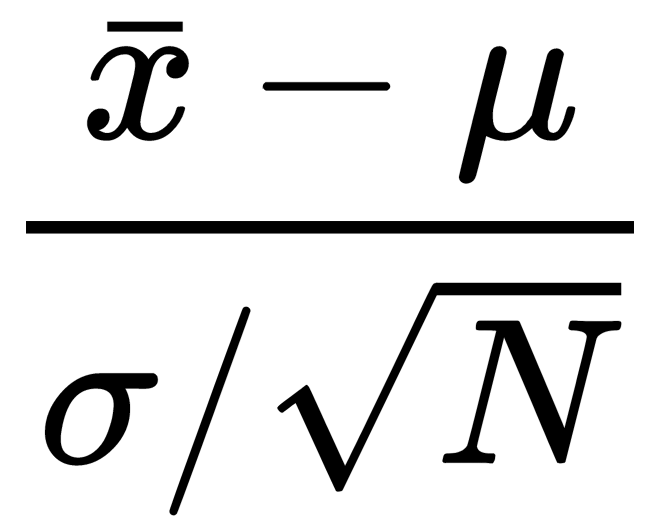approaches the Gaussian with a mean of 0 and a variance of 1. To solve the BSS problem, we need to find the matrix, , so that . Here, the  should be as close as possible to the original independent sources. We can consider this approach as the inverse process of the central limit theorem. All ICA methods are based on the same fundamental approach – finding a matrix, W, that maximizes non-Gaussianity, thereby minimizing the independence of .

The Fast ICA algorithm aims to maximize the function, 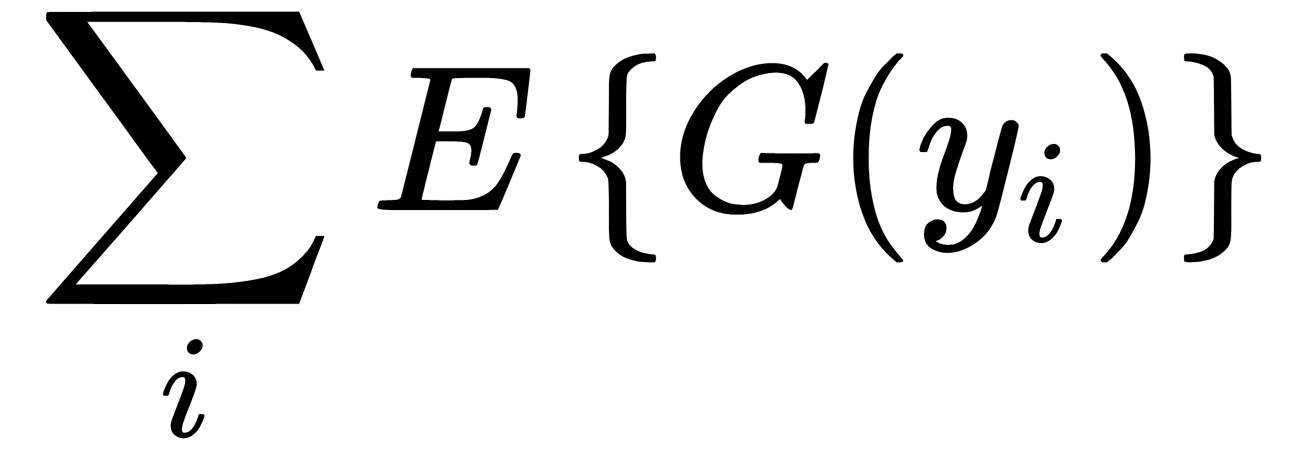, where  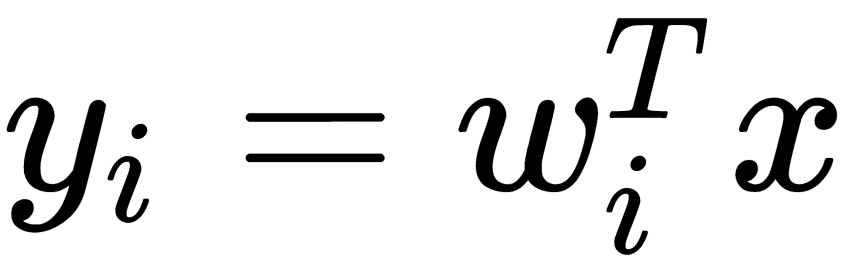are components of 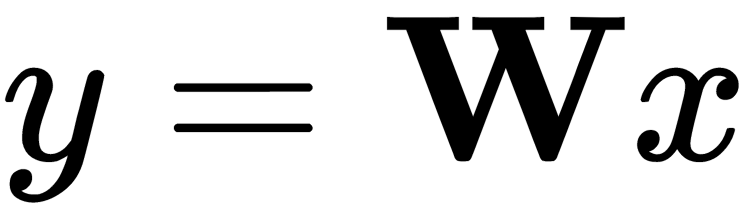. Therefore, we can rewrite the function's equation in the following form:

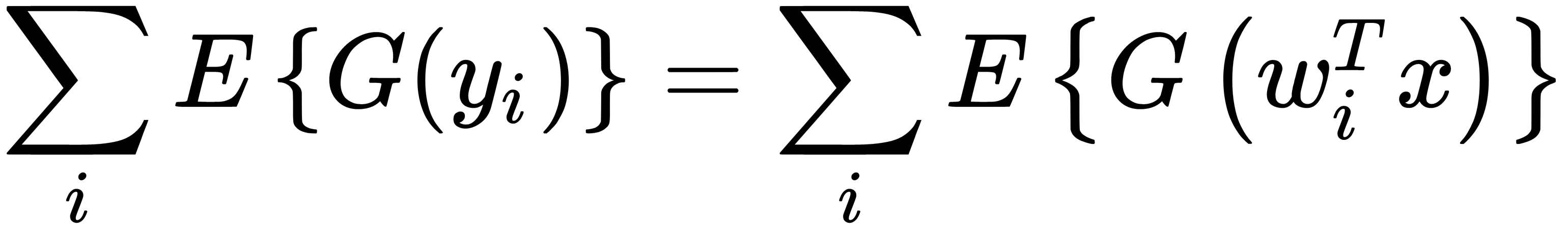
Here, the 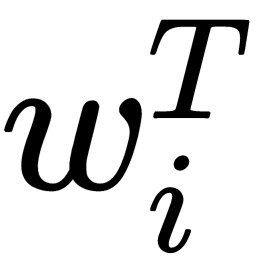 vector is the i^th row of the matrix, W.

The ICA algorithm performs the following steps:

1. Chooses the initial value of w.
2. Calculates 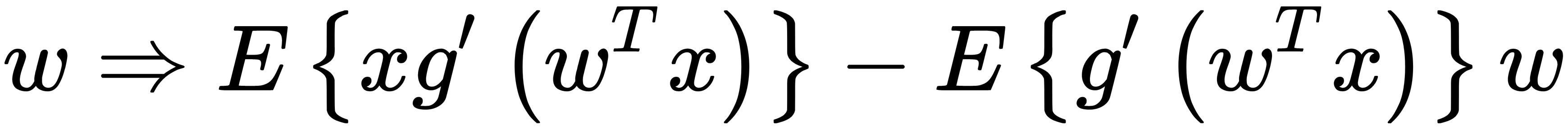, where 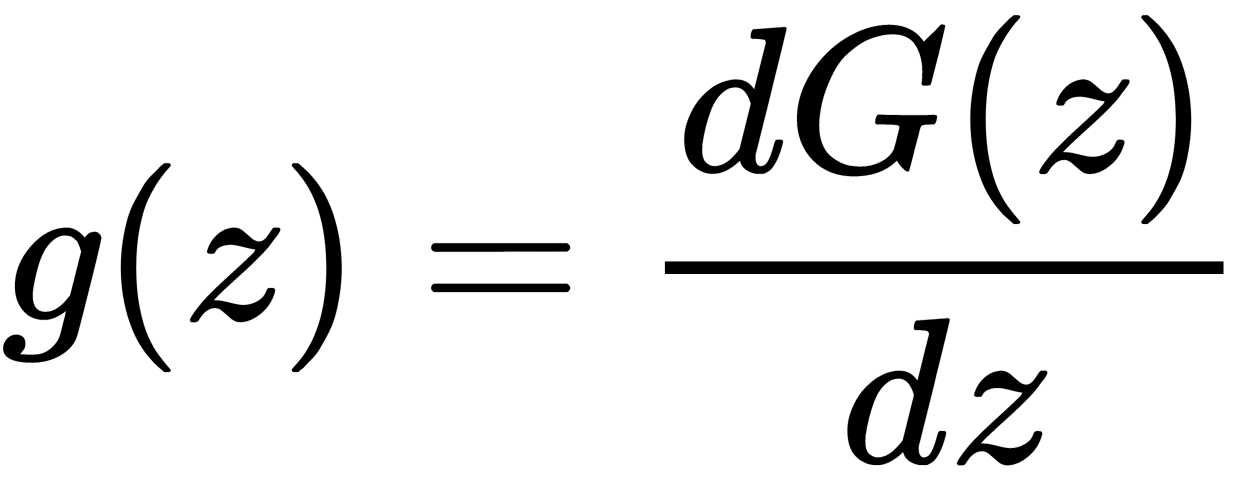is the derivative of the function, G(z).
3. Normalizes .
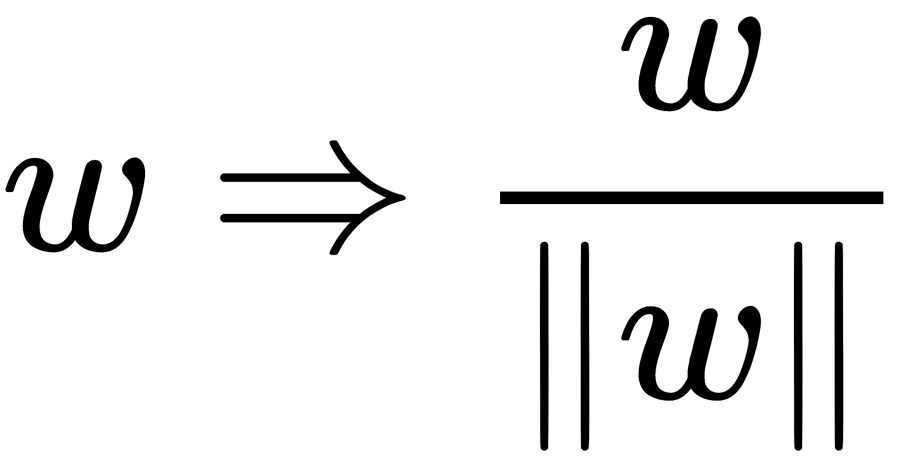4. Repeats the previous two steps until w stops changing.

To measure non-Gaussianity, Fast ICA relies on a nonquadratic nonlinear function, G (z), that can take the following forms: