Linear discriminant analysis (LDA) is a type of multivariate analysis that allows us to estimate differences between two or more groups of objects at the same time. The basis of discriminant analysis is the assumption that the descriptions of the objects of each k^th class are instances of a multidimensional random variable that's distributed according to the normal (Gaussian) law, 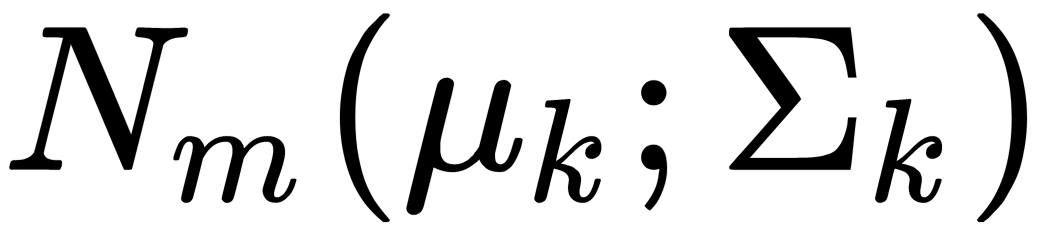, with an average, 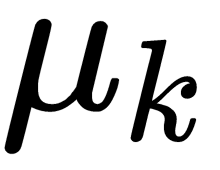_, and the following covariance matrix:

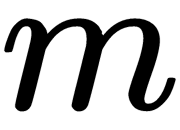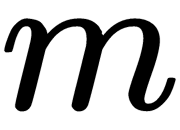The index, , indicates the dimension of the feature space. Consider a simplified geometric interpretation of the LDA algorithm for the case of two classes. Let the discriminant variables, , be the axes of the -dimensional Euclidean space. Each object (sample) is a point of this space with coordinates representing the fixed values of each variable. If both classes differ from each other in observable variables (features), they can be represented as clusters of points in different regions of the considered space that may partially overlap. To determine the position of each class, we can calculate its centroid, which is an imaginary point whose coordinates are the average values of the variables (features) in the class. The task of discriminant analysis is to create an additional  axis that passes through a cloud of points in such a way that the projections on it provide the best separability into two classes (in other words, it maximizes the distance between classes). Its position is given by a linear discriminant function (linear discriminant, LD) with weights, , that determine the contribution of each initial variable, :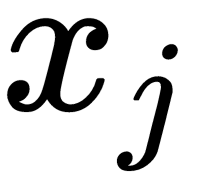

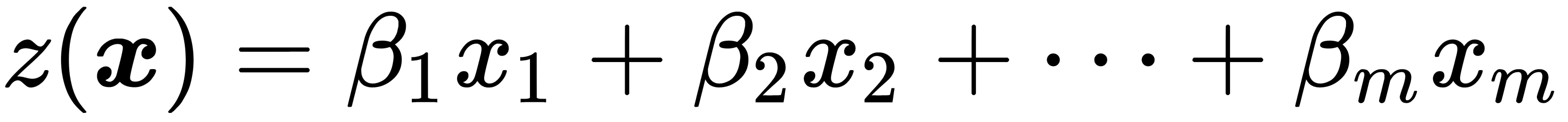
If we assume that the covariance matrices of the objects of classes 1 and 2 are equal, that is, 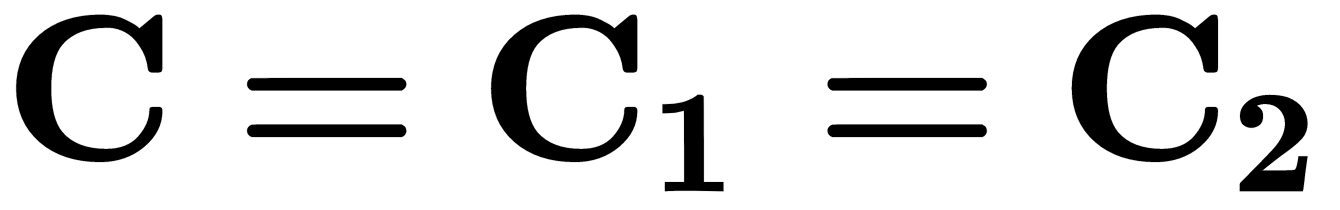, then the vector of coefficients, , of the linear discriminant, 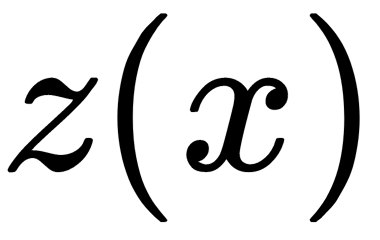, can be calculated using the formula 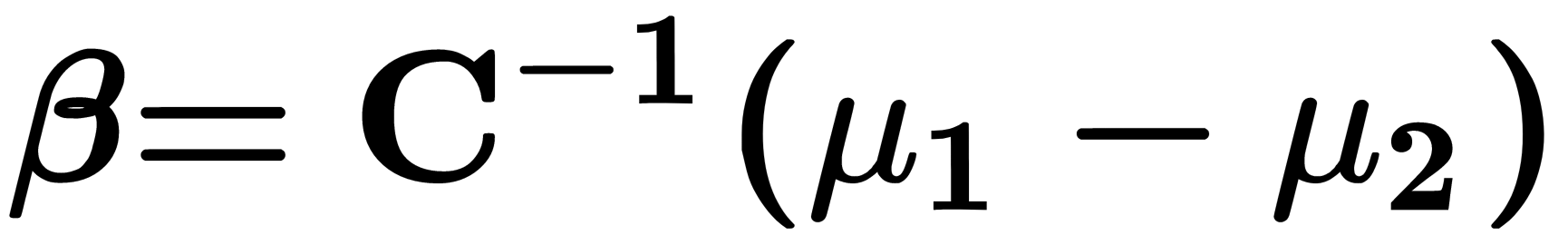, where  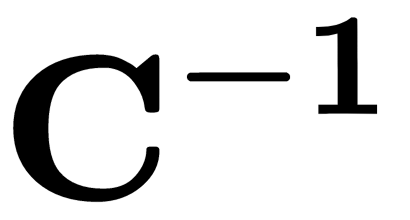is the inverse of the covariance matrix and  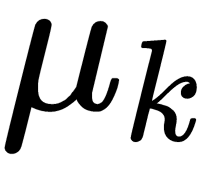is the mean of the  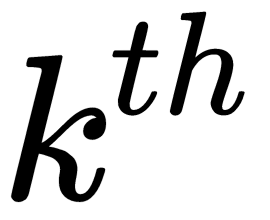class. The resulting axis coincides with the equation of a line passing through the centroids of two groups of class objects. The generalized Mahalanobis distance, which is equal to the distance between them in the multidimensional feature space, is estimated as 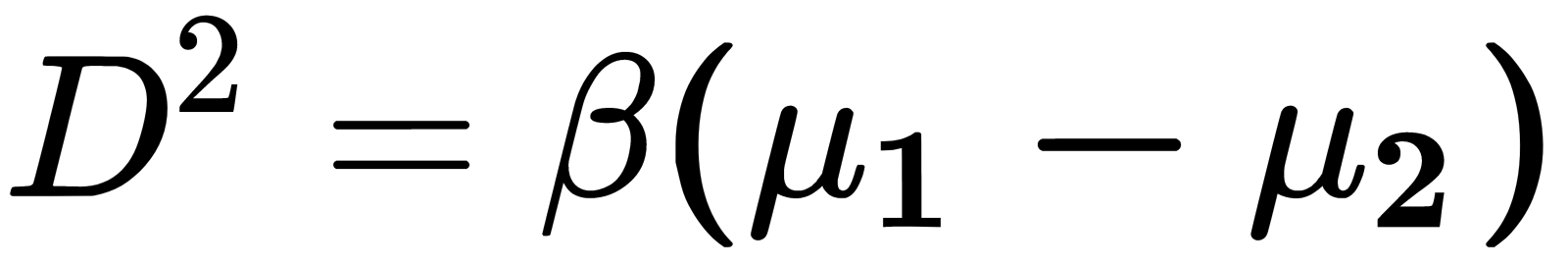. Thus, in addition to the assumption regarding the normal (Gaussian) distribution of class data, which in practice occurs quite rarely, the LDA has a stronger assumption about the statistical equality of intragroup dispersions and correlation matrices. If there are no significant differences between them, they are combined into a calculated covariance matrix, as follows:

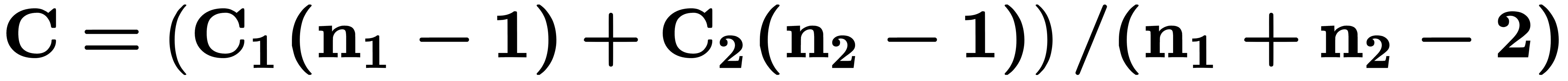
This principle can be generalized to a larger number of classes. The final algorithm may look like this:

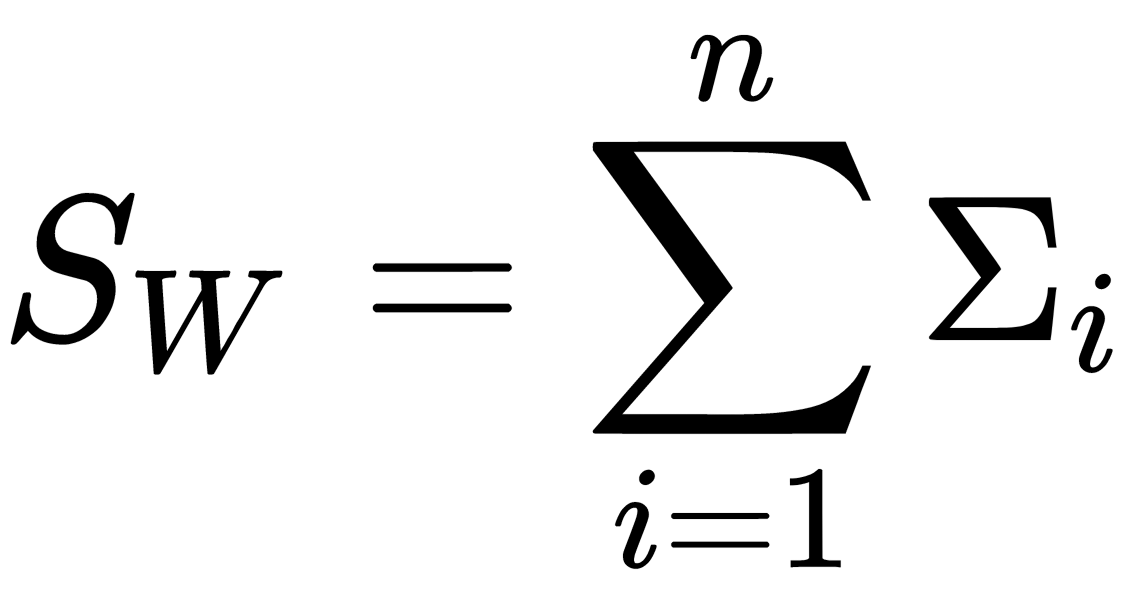
The interclass scattering matrix is calculated like this:

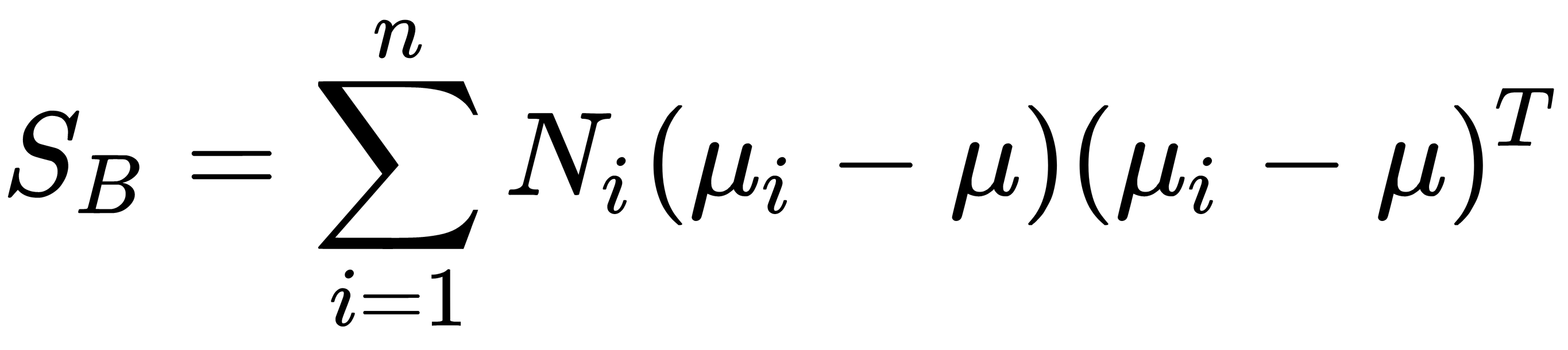
Here, 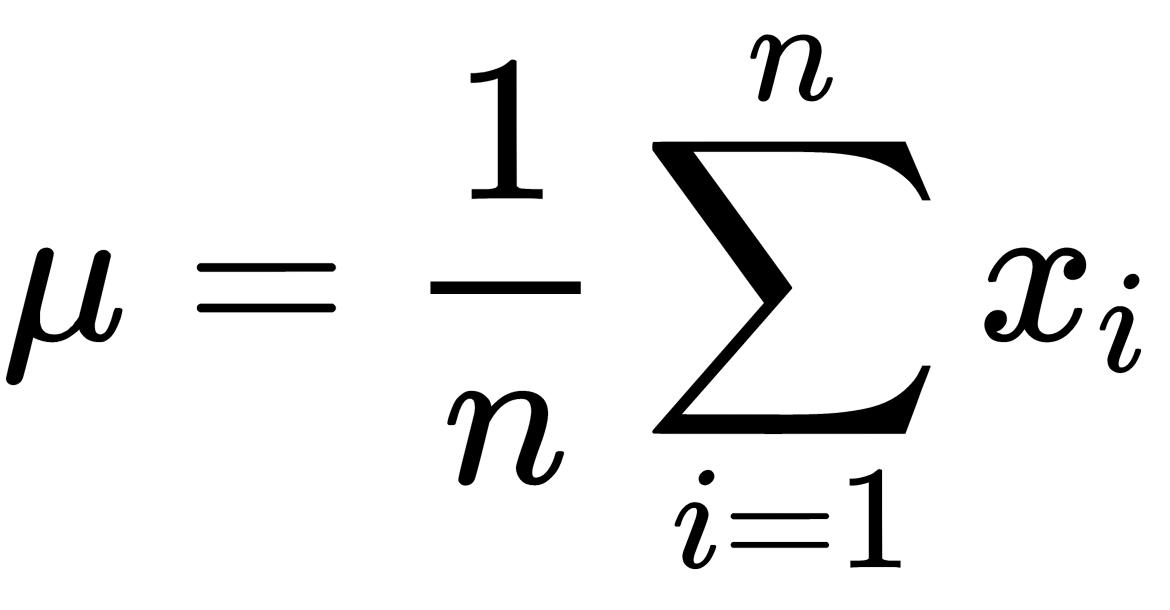_is the mean of all objects (samples),  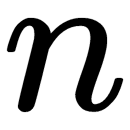is the number of classes,  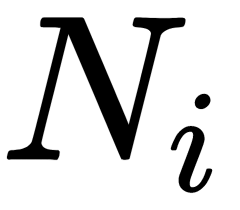is the number of objects in the i^th class, 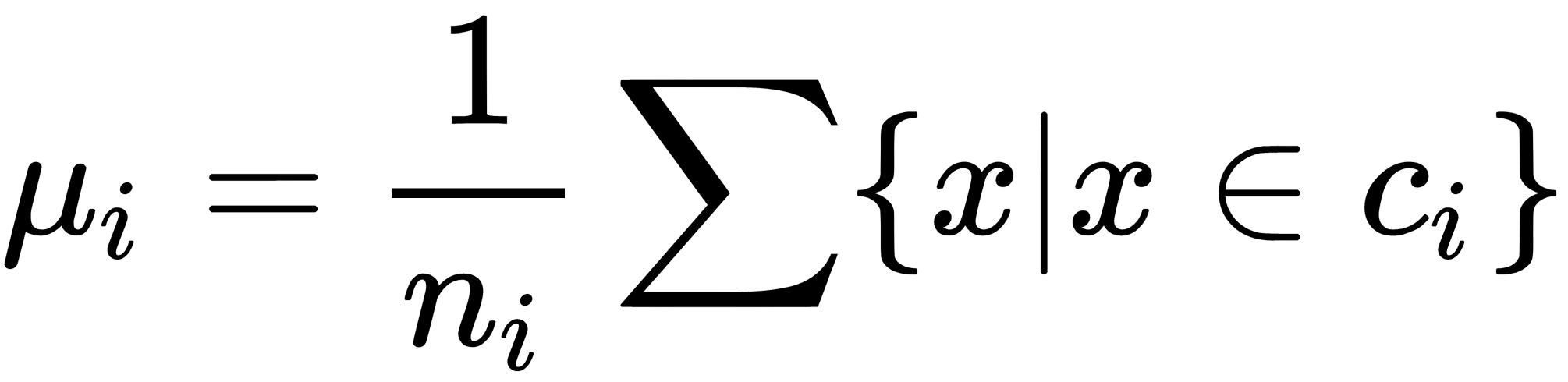is the intraclass' mean,  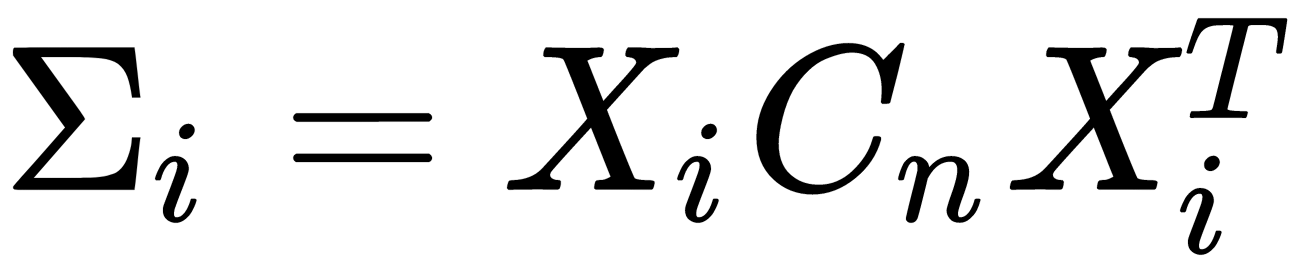is the scattering matrix for the i^th class, and  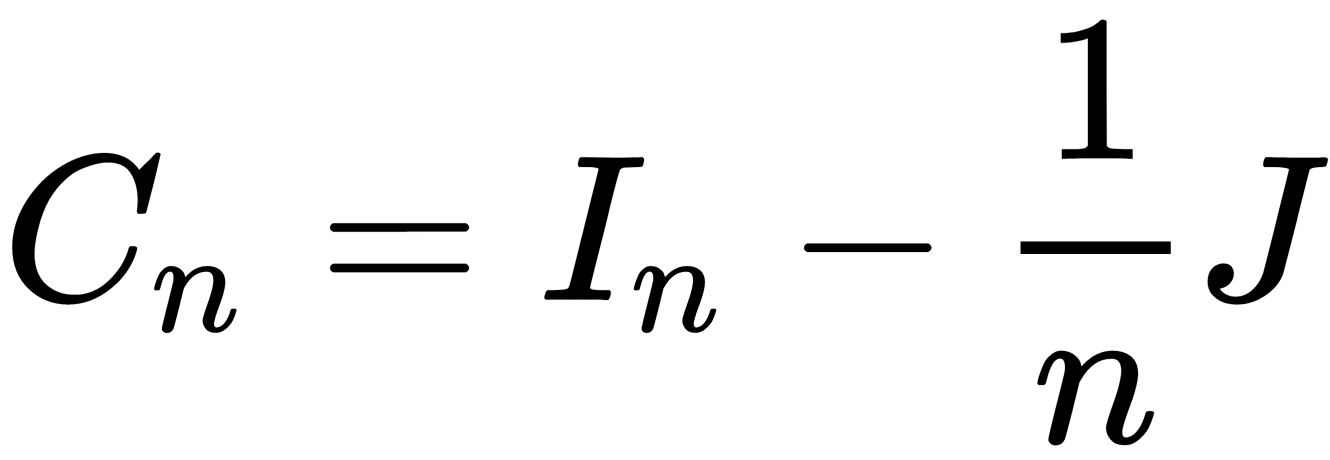is a centering matrix where  is the n x n matrix of all 1s.

Based on these matrices, the  matrix is calculated, for which the eigenvalues and the corresponding eigenvectors are determined. In the diagonal elements of the matrix, we must select the s of the largest eigenvalues and transform the matrix, leaving only the corresponding s rows in it. The resulting matrix can be used to convert all objects into the lower-dimensional space.

This method requires labeled data, meaning it is a supervised method.