Singular value decomposition (SVD) is an important method that's used to analyze data. The resulting matrix decomposition has a meaningful interpretation from a machine learning point of view. It can also be used to calculate PCA. SVD is rather slow. Therefore, when the matrices are too large, randomized algorithms are used. However, the SVD calculation is computationally more efficient than the calculation for the covariance matrix and its eigenvalues in the original PCA approach. Therefore, PCA is often implemented in terms of SVD. Let's take a look.
The essence of SVD is pure—any matrix (real or complex) is represented as a product of three matrices:

Here,  is a unitary matrix of order
is a unitary matrix of order 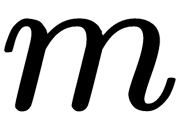 and
and  is a matrix of size
is a matrix of size  on the main diagonal, which is where there are non-negative numbers called singular values (elements outside the main diagonal are zero—such matrices are sometimes called rectangular diagonal matrices).
on the main diagonal, which is where there are non-negative numbers called singular values (elements outside the main diagonal are zero—such matrices are sometimes called rectangular diagonal matrices). is a Hermitian-conjugate
is a Hermitian-conjugate  matrix of order
matrix of order 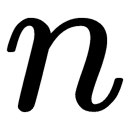 . The
. The 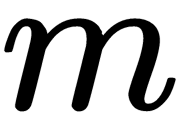 columns of the matrixes
columns of the matrixes  and
and 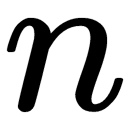 columns of the matrix
columns of the matrix  are called the left and right singular vectors of matrix
are called the left and right singular vectors of matrix  , respectively. To reduce the number of dimensions, matrix
, respectively. To reduce the number of dimensions, matrix  is important, the elements of which, when raised to the second power, can be interpreted as a variance that each component puts into a joint distribution, and they are in descending order:
is important, the elements of which, when raised to the second power, can be interpreted as a variance that each component puts into a joint distribution, and they are in descending order: 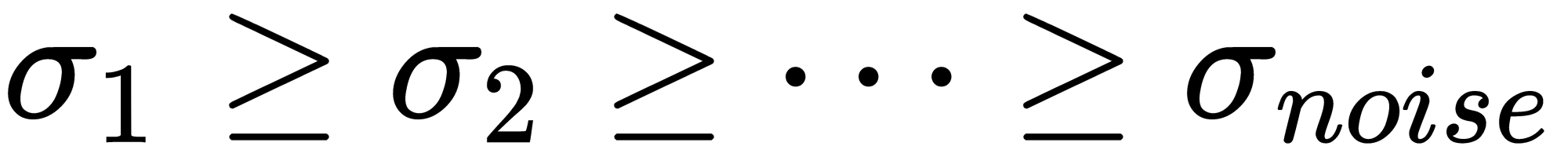 . Therefore, when we choose the number of components in SVD (as in PCA), we should take the sum of their variances into account.
. Therefore, when we choose the number of components in SVD (as in PCA), we should take the sum of their variances into account.
The relation between SVD and PCA can be described in the following way:  is the covariance matrix given by
is the covariance matrix given by 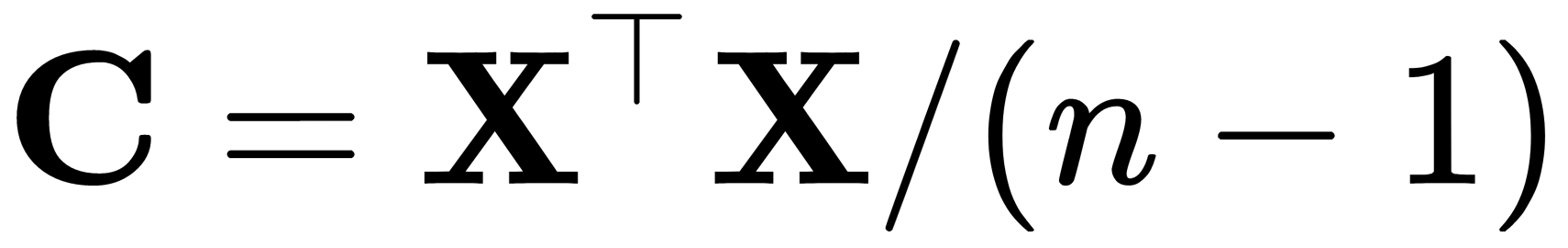 . It is a symmetric matrix, so it can be diagonalized:
. It is a symmetric matrix, so it can be diagonalized:  , where
, where  is a matrix of eigenvectors (each column is an eigenvector) and
is a matrix of eigenvectors (each column is an eigenvector) and  is a diagonal matrix of eigenvalues,
is a diagonal matrix of eigenvalues, 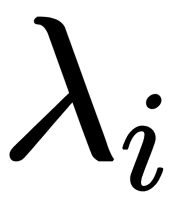 , in decreasing order on the diagonal. The eigenvectors are called principal axes or principal directions of the data. Projections of the data on the principal axes are called principal components, also known as principal component scores. They are newly transformed variables. The
, in decreasing order on the diagonal. The eigenvectors are called principal axes or principal directions of the data. Projections of the data on the principal axes are called principal components, also known as principal component scores. They are newly transformed variables. The  principal component is given by the
principal component is given by the  column of
column of  . The coordinates of the
. The coordinates of the 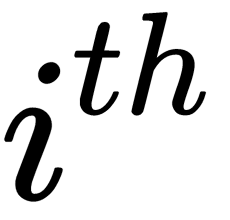 data point in the new principal component's space are given by the
data point in the new principal component's space are given by the 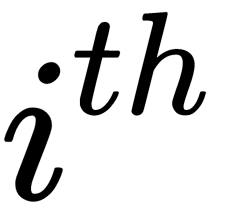 row of
row of 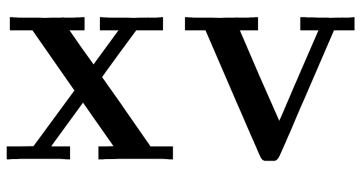 .
.
By performing SVD on  , we get
, we get  , where
, where  is a unitary matrix and
is a unitary matrix and  is the diagonal matrix of singular values,
is the diagonal matrix of singular values, 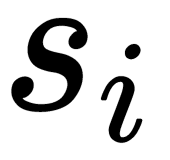 . We can observe that
. We can observe that 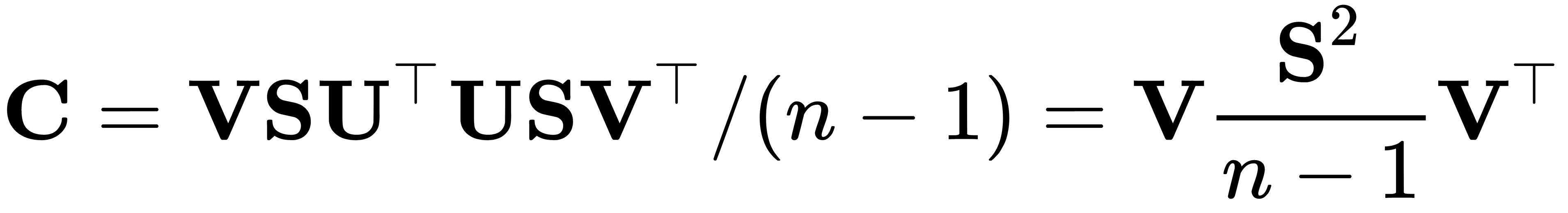 , which means that the right singular vectors,
, which means that the right singular vectors,  , are principal directions and that singular values are related to the eigenvalues of the covariance matrix via
, are principal directions and that singular values are related to the eigenvalues of the covariance matrix via 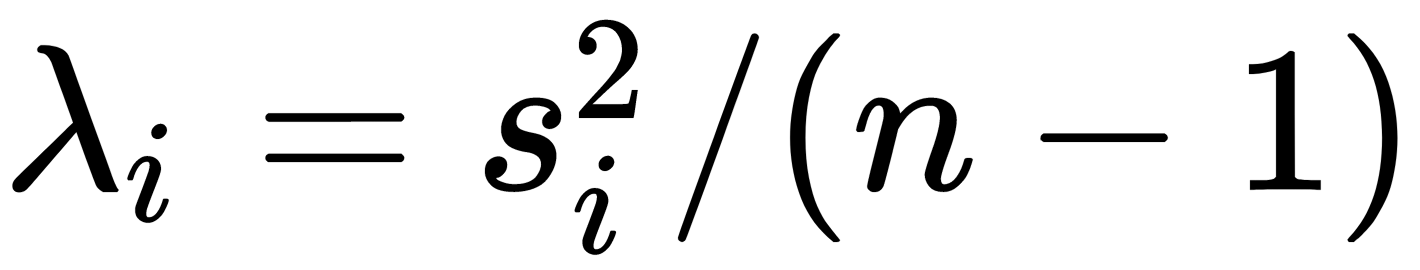 . Principal components are given by
. Principal components are given by 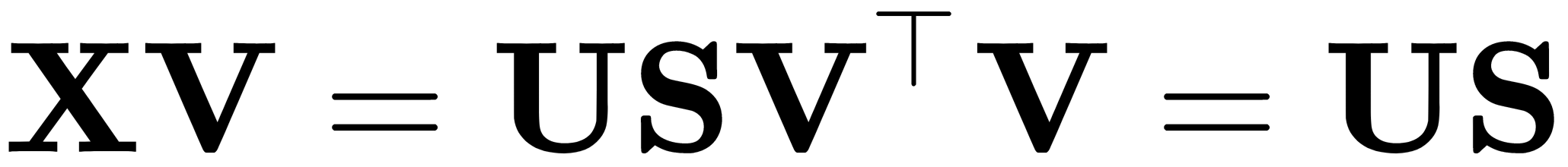 .
.
