LEARNING OBJECTIVES
After studying this chapter, you should be able to:
- 1 Identify accounting topics where the time value of money is relevant.
- 2 Distinguish between simple and compound interest.
- 3 Use appropriate compound interest tables.
- 4 Identify variables fundamental to solving interest problems.
- 5 Solve future and present value of 1 problems.
- 6 Solve future value of ordinary and annuity due problems.
- 7 Solve present value of ordinary and annuity due problems.
- 8 Solve present value problems related to deferred annuities and bonds.
- 9 Apply expected cash flows to present value measurement.
How Do I Measure That?
A significant part of accounting is measurement. And as we discussed in Chapter 2, we have a mixed-attribute measurement model. That is, many items are measured based on historical cost (e.g., property, plant, and equipment, inventory), but increasingly accounting measurements are based on fair value (e.g., financial instruments, impairments). Determining fair value of an item is fairly straightforward when market prices are available (Level 1 in the fair value hierarchy). However, when a market price is not available, accountants must rely on valuation models to develop a fair value estimate (Level 3 of the fair value hierarchy).
Developing fair value estimates based on a valuation model generally involves discounted cash flow techniques, which have three primary elements: (1) estimating the amounts and timing of future cash flows, (2) developing probability estimates for those cash flows, and (3) determining the appropriate discount rate to apply to the expected cash flows to arrive at a fair value estimate. Seems pretty straightforward, right? Actually, this can be a challenging process when applied to a variety of complex assets and liabilities for which IFRS requires a fair value estimate.
For example, many European financial institutions faced this challenge when they had to deal with losses on Greek bond holdings. Major banks, such as Crédit Agricole (FRA), Royal Bank of Scotland (GBR), and Dexia (FRA–BEL), and many others incurred substantial losses after securities markets seized up to the point that valid market prices for investment and loans were not readily available. A similar valuation challenge arose for companies with investments in auction rates securities (ARS). The fair value of ARS is generally determined at quarterly auctions. However, these auctions failed during the financial crisis, and ARS investors were forced to use a valuation model rather than market prices to determine fair value.
The IASB provides fair value estimation guidance (IFRS 13), but the Board also performs ongoing assessment of whether and to what extent additional valuation guidance is needed. In this regard, standard-setters have established advisory groups comprised of accounting and valuation professionals, preparers and users of financial statements, regulators, and other industry representatives. An example is the Valuation Resource Group (VRG). The VRG provides multiple viewpoints on application issues relating to fair value for financial reporting purposes. Here is a sampling of the issues discussed by the VRG:
- Measurement of contingent consideration in a business combination.
- Incorporating multi-period excess earnings in valuing intangible assets.
- Effects of premiums and discounts in fair value measurements.
- Determining the carrying amount of a reporting unit when performing the goodwill impairment test.
- Measurement uncertainty analysis disclosures.
As indicated, the list of topics is revealing as to the variety and complexity of the issues that must be addressed in implementing the fair value measurement principle. Discussion of these items by the VRG helped develop appropriate approaches for applying fair value guidance to specific examples. For example, with respect to the contingent consideration topic, the VRG noted that taxes must be considered when developing future cash flow estimates and that, in some cases, these tax effects are different for assets and liabilities.
The VRG provides good counsel to the standard-setters with respect to applying the fair value measurement principle. After studying this chapter, you should have a better understanding of time value of money principles and discounted cash flow techniques as they are applied in accounting measurements.
Sources: Ernst and Young, “Valuation Resource Group: Highlights of November 2010 Meeting,” Hot Topic—Update on Major Accounting and Auditing Activities, No. 2010-59 (5 November 2010).
PREVIEW OF CHAPTER 6
As we indicated in the opening story, as a financial expert in today's accounting environment, you will be expected to make present and future value measurements and to understand their implications. The purpose of this chapter is to present the tools and techniques that will help you measure the present value of future cash inflows and outflows. The content and organization of the chapter are as follows.

BASIC TIME VALUE CONCEPTS
LEARNING OBJECTIVE ![]()
Identify accounting topics where the time value of money is relevant.
In accounting (and finance), the phrase time value of money indicates a relationship between time and money—that a dollar received today is worth more than a dollar promised at some time in the future. Why? Because of the opportunity to invest today's dollar and receive interest on the investment. Yet, when deciding among investment or borrowing alternatives, it is essential to be able to compare today's dollar and tomorrow's dollar on the same footing—to “compare apples to apples.” Investors do that by using the concept of present value, which has many applications in accounting.
Applications of Time Value Concepts

Financial reporting uses different measurements in different situations—historical cost for equipment, net realizable value for inventories, fair value for investments. As we discussed in Chapter 2, the IASB increasingly is requiring the use of fair values in the measurement of assets and liabilities. According to the IASB's recent guidance on fair value measurements, the most useful fair value measures are based on market prices in active markets. Within the fair value hierarchy, these are referred to as Level 1. Recall that Level 1 fair value measures are the most reliable because they are based on quoted prices, such as a closing share price.
However, for many assets and liabilities, market-based fair value information is not readily available. In these cases, fair value can be estimated based on the expected future cash flows related to the asset or liability. Such fair value estimates are generally considered Level 3 (least reliable) in the fair value hierarchy because they are based on unobservable inputs, such as a company's own data or assumptions related to the expected future cash flows associated with the asset or liability. As discussed in the fair value guidance, present value techniques are used to convert expected cash flows into present values, which represent an estimate of fair value. [1]
![]() See the Authoritative Literature section (page 270).
See the Authoritative Literature section (page 270).
Because of the increased use of present values in this and other contexts, it is important to understand present value techniques.1 We list some of the applications of present value-based measurements to accounting topics below; we discuss many of these in the following chapters.
PRESENT VALUE-BASED ACCOUNTING MEASUREMENTS
1. NOTES. Valuing long-term receivables and payables that carry no stated interest rate or a lower than market interest rate.
2. LEASES. Valuing assets and obligations to be capitalized under long-term leases and measuring the amount of the lease payments and annual leasehold amortization.
3. PENSIONS AND OTHER POSTRETIREMENT BENEFITS. Measuring service cost components of employers' postretirement benefits expense and postretirement benefits obligation.
4. LONG-TERM ASSETS. Evaluating alternative long-term investments by discounting future cash flows. Determining the value of assets acquired under deferred payment contracts. Measuring impairments of assets.
5. SHARE-BASED COMPENSATION. Determining the fair value of employee services in compensatory share-option plans.
6. BUSINESS COMBINATIONS. Determining the value of receivables, payables, liabilities, accruals, and commitments acquired or assumed in a “purchase.”
7. DISCLOSURES. Measuring the value of future cash flows from oil and gas reserves for disclosure in supplementary information.
8. ENVIRONMENTAL LIABILITIES. Determining the fair value of future obligations for asset retirements.
In addition to accounting and business applications, compound interest, annuity, and present value concepts apply to personal finance and investment decisions. In purchasing a home or car, planning for retirement, and evaluating alternative investments, you will need to understand time value of money concepts.
The Nature of Interest
Interest is payment for the use of money. It is the excess cash received or repaid over and above the amount lent or borrowed (principal). For example, Corner Bank lends Hillfarm Company $10,000 with the understanding that it will repay $11,500. The excess over $10,000, or $1,500, represents interest expense.
The lender generally states the amount of interest as a rate over a specific period of time. For example, if Hillfarm borrowed $10,000 for one year before repaying $11,500, the rate of interest is 15% per year ($1,500 ÷ $10,000). The custom of expressing interest as a percentage rate is an established business practice.2 In fact, business managers make investing and borrowing decisions on the basis of the rate of interest involved, rather than on the actual dollar amount of interest to be received or paid.
How is the interest rate determined? One important factor is the level of credit risk (risk of non-payment) involved. Other factors being equal, the higher the credit risk, the higher the interest rate. Low-risk borrowers like Nokia (FIN) or adidas (DEU) can probably obtain a loan at or slightly below the going market rate of interest. However, a bank would probably charge the neighborhood bakery several percentage points above the market rate, if granting the loan at all.
The amount of interest involved in any financing transaction is a function of three variables:
VARIABLES IN INTEREST COMPUTATION
1. PRINCIPAL. The amount borrowed or invested.
2. INTEREST RATE. A percentage of the outstanding principal.
3. TIME. The number of years or fractional portion of a year that the principal is outstanding.
Thus, the following three relationships apply:
- The larger the principal amount, the larger the dollar amount of interest.
- The higher the interest rate, the larger the dollar amount of interest.
- The longer the time period, the larger the dollar amount of interest.
Simple Interest
Companies compute simple interest on the amount of the principal only. It is the return on (or growth of) the principal for one time period. The following equation expresses simple interest.3
![]()
where

To illustrate, Barstow Electric Inc. borrows $10,000 for 3 years with a simple interest rate of 8% per year. It computes the total interest it will pay as follows.

If Barstow borrows $10,000 for 3 months at 8%, the interest is $200, computed as follows.
![]()
Compound Interest
LEARNING OBJECTIVE ![]()
Use appropriate compound interest tables.
John Maynard Keynes, the legendary English economist, supposedly called it magic. Mayer Rothschild, the founder of the famous European banking firm, proclaimed it the eighth wonder of the world. Today, people continue to extol its wonder and its power. The object of their affection? Compound interest.
We compute compound interest on principal and on any interest earned that has not been paid or withdrawn. It is the return on (or growth of) the principal for two or more time periods. Compounding computes interest not only on the principal but also on the interest earned to date on that principal, assuming the interest is left on deposit.
To illustrate the difference between simple and compound interest, assume that Vasquez Company deposits $10,000 in the Last National Bank, where it will earn simple interest of 9% per year. It deposits another $10,000 in the First State Bank, where it will earn compound interest of 9% per year compounded annually. In both cases, Vasquez will not withdraw any interest until 3 years from the date of deposit. Illustration 6-1 shows the computation of interest Vasquez will receive, as well as its accumulated year-end balance.
ILLUSTRATION 6-1
Simple vs. Compound Interest
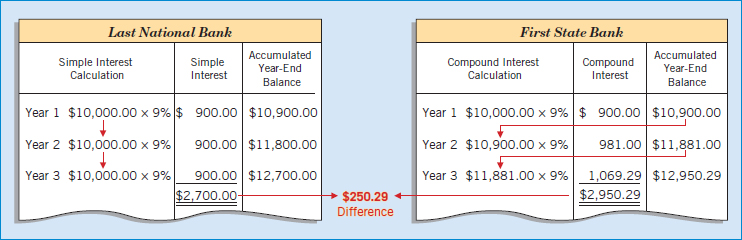
Note in Illustration 6-1 that simple interest uses the initial principal of $10,000 to compute the interest in all 3 years. Compound interest uses the accumulated balance (principal plus interest to date) at each year-end to compute interest in the succeeding year. This explains the larger balance in the compound interest account.
Obviously, any rational investor would choose compound interest, if available, over simple interest. In the example above, compounding provides $250.29 of additional interest revenue. For practical purposes, compounding assumes that unpaid interest earned becomes a part of the principal. Furthermore, the accumulated balance at the end of each year becomes the new principal sum on which interest is earned during the next year.
Compound interest is the typical interest computation applied in business situations. This occurs particularly in our economy, where companies use and finance large amounts of long-lived assets over long periods of time. Financial managers view and evaluate their investment opportunities in terms of a series of periodic returns, each of which they can reinvest to yield additional returns. Simple interest usually applies only to short-term investments and debts that involve a time span of one year or less.
What do the numbers mean? A PRETTY GOOD START
The continuing debate by governments as to how to provide retirement benefits to their citizens serves as a great context to illustrate the power of compounding. One proposed idea is for the government to give $1,000 to every citizen at birth. This gift would be deposited in an account that would earn interest tax-free until the citizen retires. Assuming the account earns a 5% annual return until retirement at age 65, the $1,000 would grow to $23,839. With monthly compounding, the $1,000 deposited at birth would grow to $25,617.
Why start so early? If the government waited until age 18 to deposit the money, it would grow to only $9,906 with annual compounding. That is, reducing the time invested by a third results in more than a 50% reduction in retirement money. This example illustrates the importance of starting early when the power of compounding is involved.
Compound Interest Tables (see pages 284–293)
We present five different types of compound interest tables at the end of this chapter. These tables should help you study this chapter as well as solve other problems involving interest.
INTEREST TABLES AND THEIR CONTENTS
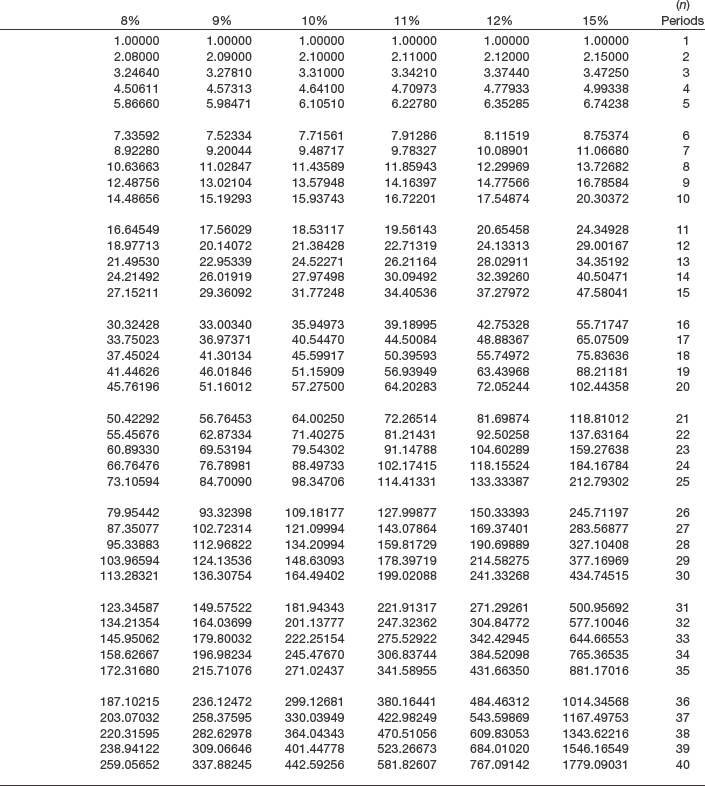
1. FUTURE VALUE OF 1 TABLE. Contains the amounts to which 1 will accumulate if deposited now at a specified rate and left for a specified number of periods (Table 6-1).
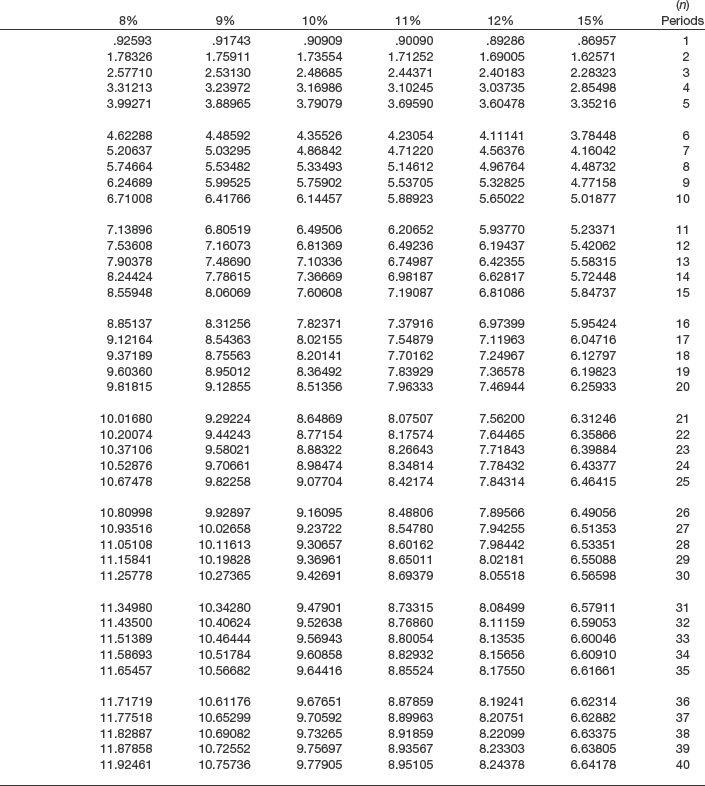
2. PRESENT VALUE OF 1 TABLE. Contains the amounts that must be deposited now at a specified rate of interest to equal 1 at the end of a specified number of periods (Table 6-2).
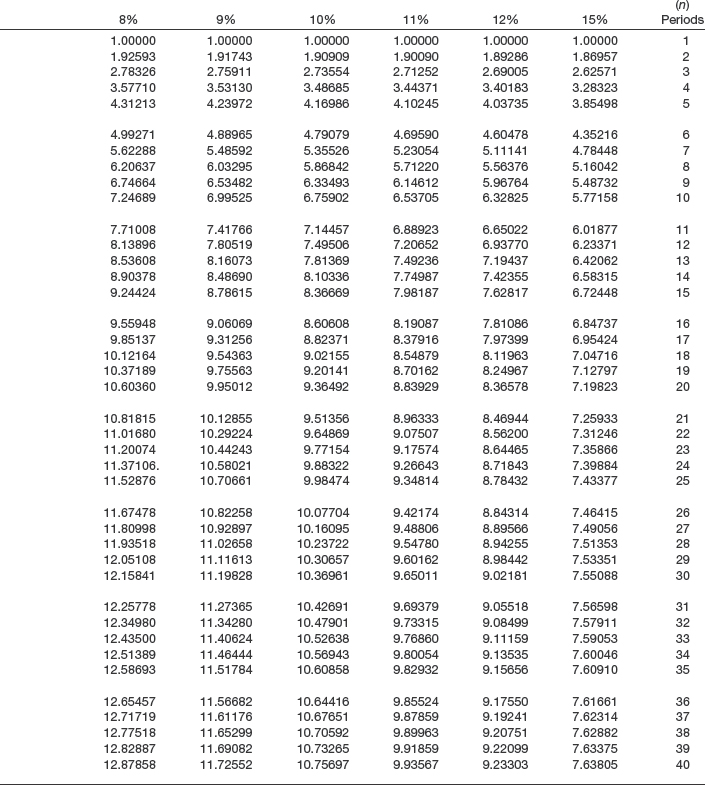
3. FUTURE VALUE OF AN ORDINARY ANNUITY OF 1 TABLE. Contains the amounts to which periodic rents of 1 will accumulate if the payments (rents) are invested at the end of each period at a specified rate of interest for a specified number of periods (Table 6-3).
4. PRESENT VALUE OF AN ORDINARY ANNUITY OF 1 TABLE. Contains the amounts that must be deposited now at a specified rate of interest to permit withdrawals of 1 at the end of regular periodic intervals for the specified number of periods (Table 6-4).
5. PRESENT VALUE OF AN ANNUITY DUE OF 1 TABLE. Contains the amounts that must be deposited now at a specified rate of interest to permit withdrawals of 1 at the beginning of regular periodic intervals for the specified number of periods (Table 6-5).
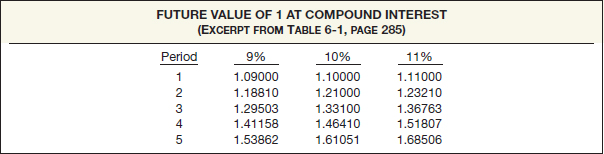
Illustration 6-2 presents the general format and content of these tables. It shows how much principal plus interest a dollar accumulates to at the end of each of five periods, at three different rates of compound interest.
ILLUSTRATION 6-2
Excerpt from Table 6-1
The compound tables rely on basic formulas. For example, the formula to determine the future value factor (FVF) for 1 is:
![]()
where
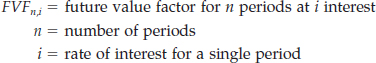
Financial calculators include preprogrammed FVFn,i and other time value of money formulas.
To illustrate the use of interest tables to calculate compound amounts, assume an interest rate of 9%. Illustration 6-3 shows the future value to which 1 accumulates (the future value factor).
ILLUSTRATION 6-3
Accumulation of Compound Amounts

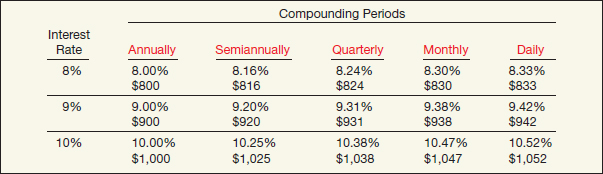
Throughout our discussion of compound interest tables, note the intentional use of the term periods instead of years. Interest is generally expressed in terms of an annual rate. However, many business circumstances dictate a compounding period of less than one year. In such circumstances, a company must convert the annual interest rate to correspond to the length of the period. To convert the “annual interest rate” into the “compounding period interest rate,” a company divides the annual rate by the number of compounding periods per year.
In addition, companies determine the number of periods by multiplying the number of years involved by the number of compounding periods per year. To illustrate, assume an investment of $1 for 6 years at 8% annual interest compounded quarterly. Using Table 6-1, page 284, read the factor that appears in the 2% column on the 24th row—6 years × 4 compounding periods per year, namely 1.60844, or approximately $1.61. Thus, all compound interest tables use the term periods, not years, to express the quantity of n. Illustration 6-4 shows how to determine (1) the interest rate per compounding period and (2) the number of compounding periods in four situations of differing compounding frequency.4
ILLUSTRATION 6-4
Frequency of Compounding

How often interest is compounded can substantially affect the rate of return. For example, a 9% annual interest compounded daily provides a 9.42% yield, or a difference of 0.42%. The 9.42% is the effective yield.5 The annual interest rate (9%) is the stated, nominal, or face rate. When the compounding frequency is greater than once a year, the effective-interest rate will always exceed the stated rate.
Illustration 6-5 shows how compounding for five different time periods affects the effective yield and the amount earned by an investment of $10,000 for one year.
ILLUSTRATION 6-5
Comparison of Different Compounding Periods
Fundamental Variables
LEARNING OBJECTIVE ![]()
Identify variables fundamental to solving interest problems.
The following four variables are fundamental to all compound interest problems.
FUNDAMENTAL VARIABLES
1. RATE OF INTEREST. This rate, unless otherwise stated, is an annual rate that must be adjusted to reflect the length of the compounding period if less than a year.
2. NUMBER OF TIME PERIODS. This is the number of compounding periods. (A period may be equal to or less than a year.)
3. FUTURE VALUE. The value at a future date of a given sum or sums invested assuming compound interest.
*. PRESENT VALUE. The value now (present time) of a future sum or sums discounted assuming compound interest.
Illustration 6-6 depicts the relationship of these four fundamental variables in a time diagram.
ILLUSTRATION 6-6
Basic Time Diagram

In some cases, all four of these variables are known. However, at least one variable is unknown in many business situations. To better understand and solve the problems in this chapter, we encourage you to sketch compound interest problems in the form of the preceding time diagram.
SINGLE-SUM PROBLEMS
LEARNING OBJECTIVE ![]()
Solve future and present value of 1 problems.
Many business and investment decisions involve a single amount of money that either exists now or will in the future. Single-sum problems are generally classified into one of the following two categories.
1. Computing the unknown future value of a known single sum of money that is invested now for a certain number of periods at a certain interest rate.
2. Computing the unknown present value of a known single sum of money in the future that is discounted for a certain number of periods at a certain interest rate.
When analyzing the information provided, determine first whether the problem involves a future value or a present value. Then apply the following general rules, depending on the situation:
- If solving for a future value, accumulate all cash flows to a future point. In this instance, interest increases the amounts or values over time so that the future value exceeds the present value.
- If solving for a present value, discount all cash flows from the future to the present. In this case, discounting reduces the amounts or values, so that the present value is less than the future amount.
Preparation of time diagrams aids in identifying the unknown as an item in the future or the present. Sometimes the problem involves neither a future value nor a present value. Instead, the unknown is the interest or discount rate, or the number of compounding or discounting periods.
Future Value of a Single Sum
To determine the future value of a single sum, multiply the future value factor by its present value (principal), as follows.
![]()
where

To illustrate, Bruegger Co. wants to determine the future value of €50,000 invested for 5 years compounded annually at an interest rate of 11%. Illustration 6-7 shows this investment situation in time-diagram form.
ILLUSTRATION 6-7
Future Value Time Diagram (n = 5, i = 11%)

Using the future value formula, Bruegger solves this investment problem as follows.

To determine the future value factor of 1.68506 in the formula above, Bruegger uses a financial calculator or reads the appropriate table, in this case Table 6-1 (11% column, 5-period row).
Companies can apply this time diagram and formula approach to routine business situations. To illustrate, assume that Shanghai Electric Power (CHN) deposited ¥250 million in an escrow account with Industrial and Commercial Bank of China (CHN) at the beginning of 2015 as a commitment toward a power plant to be completed December 31, 2018. How much will the company have on deposit at the end of 4 years if interest is 10%, compounded semiannually?
With a known present value of ¥250 million, a total of 8 compounding periods (4 × 2), and an interest rate of 5% per compounding period (.10 ÷ 2), the company can time-diagram this problem and determine the future value, as shown in Illustration 6-8.
ILLUSTRATION 6-8
Future Value Time Diagram (n = 8, i = 5%)
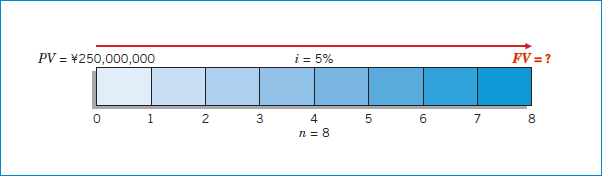
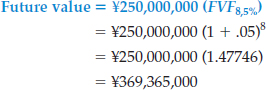
Using a future value factor found in Table 1 (5% column, 8-period row), we find that the deposit of ¥250 million will accumulate to ¥369,365,000 by December 31, 2018.
Present Value of a Single Sum
The Bruegger example (on page 247) shows that €50,000 invested at an annually compounded interest rate of 11% will equal €84,253 at the end of 5 years. It follows, then, that €84,253, 5 years in the future, is worth €50,000 now. That is, €50,000 is the present value of €84,253. The present value is the amount needed to invest now, to produce a known future value.
The present value is always a smaller amount than the known future value, due to earned and accumulated interest. In determining the future value, a company moves forward in time using a process of accumulation. In determining present value, it moves backward in time using a process of discounting.
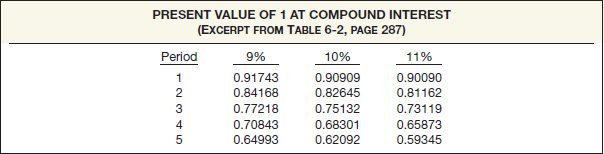
As indicated earlier, a “present value of 1 table” appears at the end of this chapter as Table 6-2. Illustration 6-9 demonstrates the nature of such a table. It shows the present value of 1 for five different periods at three different rates of interest.
ILLUSTRATION 6-9
Excerpt from Table 6-2
The following formula is used to determine the present value of 1 (present value factor).
![]()
where
![]()
To illustrate, assuming an interest rate of 9%, the present value of 1 discounted for three different periods is as shown in Illustration 6-10.
ILLUSTRATION 6-10
Present Value of 1 Discounted at 9% for Three Periods

The present value of any single sum (future value), then, is as follows.
![]()
where
To illustrate, what is the present value of €84,253 to be received or paid in 5 years discounted at 11% compounded annually? Illustration 6-11 shows this problem as a time diagram.
ILLUSTRATION 6-11
Present Value Time Diagram (n = 5, i = 11%)

Using the formula, we solve this problem as follows.

To determine the present value factor of 0.59345, use a financial calculator or read the present value of a single sum in Table 6-2 (11% column, 5-period row).
The time diagram and formula approach can be applied in a variety of situations. For example, assume that your rich uncle decides to give you $2,000 for a vacation when you graduate from college 3 years from now. He proposes to finance the trip by investing a sum of money now at 8% compound interest that will provide you with $2,000 upon your graduation. The only conditions are that you graduate and that you tell him how much to invest now.
To impress your uncle, you set up the time diagram in Illustration 6-12 and solve this problem as follows.
ILLUSTRATION 6-12
Present Value Time Diagram (n = 3, i = 8%)


Advise your uncle to invest $1,587.66 now to provide you with $2,000 upon graduation. To satisfy your uncle's other condition, you must pass this course (and many more).
Solving for Other Unknowns in Single-Sum Problems
In computing either the future value or the present value in the previous single-sum illustrations, both the number of periods and the interest rate were known. In many business situations, both the future value and the present value are known, but the number of periods or the interest rate is unknown. The following two examples are single-sum problems (future value and present value) with either an unknown number of periods (n) or an unknown interest rate (i). These examples, and the accompanying solutions, demonstrate that knowing any three of the four values (future value, FV; present value, PV; number of periods, n; interest rate, i) allows you to derive the remaining unknown variable.
Example–Computation of the Number of Periods
The Village of Somonauk wants to accumulate $70,000 for the construction of a veterans monument in the town square. At the beginning of the current year, the Village deposited $47,811 in a memorial fund that earns 10% interest compounded annually. How many years will it take to accumulate $70,000 in the memorial fund?
In this illustration, the Village knows both the present value ($47,811) and the future value ($70,000), along with the interest rate of 10%. Illustration 6-13 depicts this investment problem as a time diagram.
ILLUSTRATION 6-13
Time Diagram to Solve for Unknown Number of Periods

Knowing both the present value and the future value allows the Village to solve for the unknown number of periods. It may use either the future value or the present value formulas, as shown in Illustration 6-14.
ILLUSTRATION 6-14
Solving for Unknown Number of Periods

Using the future value factor of 1.46410, refer to Table 6-1 and read down the 10% column to find that factor in the 4-period row. Thus, it will take 4 years for the $47,811 to accumulate to $70,000 if invested at 10% interest compounded annually. Or, using the present value factor of 0.68301, refer to Table 6-2 and read down the 10% column to find that factor in the 4-period row.
Example–Computation of the Interest Rate
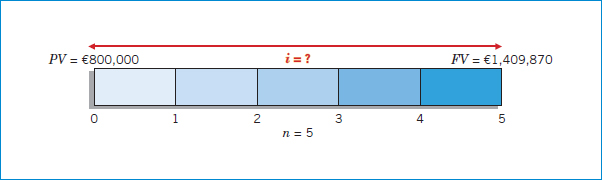
Advanced Design, Inc. needs €1,409,870 for basic research 5 years from now. The company currently has €800,000 to invest for that purpose. At what rate of interest must it invest the €800,000 to fund basic research projects of €1,409,870, 5 years from now?
The time diagram in Illustration 6-15 depicts this investment situation.
ILLUSTRATION 6-15
Time Diagram to Solve for Unknown Interest Rate
Advanced Design may determine the unknown interest rate from either the future value approach or the present value approach, as Illustration 6-16 shows.
ILLUSTRATION 6-16
Solving for Unknown Interest Rate

Using the future value factor of 1.76234, refer to Table 6-1 and read across the 5-period row to find that factor in the 12% column. Thus, the company must invest the €800,000 at 12% to accumulate to €1,409,870 in 5 years. Or, using the present value factor of .56743 and Table 6-2, again find that factor at the juncture of the 5-period row and the 12% column.
ANNUITIES
The preceding discussion involved only the accumulation or discounting of a single principal sum. However, many situations arise in which a series of dollar amounts are paid or received periodically, such as installment loans or sales; regular, partially recovered invested funds; or a series of realized cost savings.
![]() LEARNING OBJECTIVE
LEARNING OBJECTIVE
Solve future value of ordinary and annuity due problems.
For example, a life insurance contract involves a series of equal payments made at equal intervals of time. Such a process of periodic payment represents the accumulation of a sum of money through an annuity. An annuity, by definition, requires the following: (1) periodic payments or receipts (called rents) of the same amount, (2) the same-length interval between such rents, and (3) compounding of interest once each interval. The future value of an annuity is the sum of all the rents plus the accumulated compound interest on them.
Note that the rents may occur at either the beginning or the end of the periods. If the rents occur at the end of each period, an annuity is classified as an ordinary annuity. If the rents occur at the beginning of each period, an annuity is classified as an annuity due.
Future Value of an Ordinary Annuity
One approach to determining the future value of an annuity computes the value to which each of the rents in the series will accumulate, and then totals their individual future values.
For example, assume that $1 is deposited at the end of each of 5 years (an ordinary annuity) and earns 12% interest compounded annually. Illustration 6-17 shows the computation of the future value, using the “future value of 1” table (Table 6-1) for each of the five $1 rents.
ILLUSTRATION 6-17
Solving for the Future Value of an Ordinary Annuity
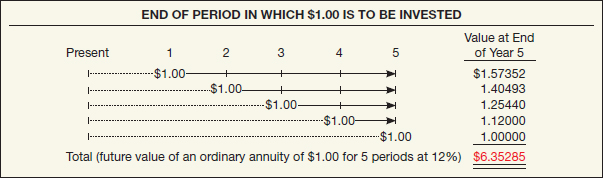
Because an ordinary annuity consists of rents deposited at the end of the period, those rents earn no interest during the period. For example, the third rent earns interest for only two periods (periods four and five). It earns no interest for the third period since it is not deposited until the end of the third period. When computing the future value of an ordinary annuity, the number of compounding periods will always be one less than the number of rents.
The foregoing procedure for computing the future value of an ordinary annuity always produces the correct answer. However, it can become cumbersome if the number of rents is large. A formula provides a more efficient way of expressing the future value of an ordinary annuity of 1. This formula sums the individual rents plus the compound interest, as follows.
![]()
where
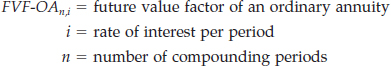
For example, FVF-OA5,12% refers to the value to which an ordinary annuity of 1 will accumulate in 5 periods at 12% interest.
Using the formula above has resulted in the development of tables, similar to those used for the “future value of 1” and the “present value of 1” for both an ordinary annuity and an annuity due. Illustration 6-18 provides an excerpt from the “future value of an ordinary annuity of 1” table.
ILLUSTRATION 6-18
Excerpt from Table 6-3

Interpreting the table, if $1 is invested at the end of each year for 4 years at 11% interest compounded annually, the value of the annuity at the end of the fourth year is $4.71 (4.70973 × $1.00). Now, multiply the factor from the appropriate line and column of the table by the dollar amount of one rent involved in an ordinary annuity. The result: the accumulated sum of the rents and the compound interest to the date of the last rent.
The following formula computes the future value of an ordinary annuity.
![]()
where

To illustrate, what is the future value of five $5,000 deposits made at the end of each of the next 5 years, earning interest of 12%? Illustration 6-19 depicts this problem as a time diagram.
ILLUSTRATION 6-19
Time Diagram for Future Value of Ordinary Annuity (n = 5, i = 12%)

Use of the formula solves this investment problem as follows.
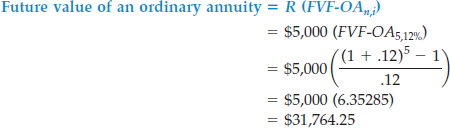
To determine the future value of an ordinary annuity factor of 6.35285 in the formula above, use a financial calculator or read the appropriate table, in this case, Table 6-3 (12% column, 5-period row).
To illustrate these computations in a business situation, assume that Hightown Electronics deposits $75,000 at the end of each 6-month period for the next 3 years, to accumulate enough money to meet debts that mature in 3 years. What is the future value that the company will have on deposit at the end of 3 years if the annual interest rate is 10%? The time diagram in Illustration 6-20 depicts this situation.
ILLUSTRATION 6-20
Time Diagram for Future Value of Ordinary Annuity (n = 6, i = 5%)

The formula solution for the Hightown Electronics situation is as follows.
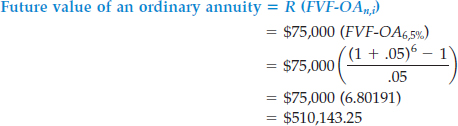
Thus, six 6-month deposits of $75,000 earning 5% per period will grow to $510,143.25.
Future Value of an Annuity Due
The preceding analysis of an ordinary annuity assumed that the periodic rents occur at the end of each period. Recall that an annuity due assumes periodic rents occur at the beginning of each period. This means an annuity due will accumulate interest during the first period (in contrast to an ordinary annuity rent, which will not). In other words, the two types of annuities differ in the number of interest accumulation periods involved.
If rents occur at the end of a period (ordinary annuity), in determining the future value of an annuity there will be one less interest period than if the rents occur at the beginning of the period (annuity due). Illustration 6-21 shows this distinction.
ILLUSTRATION 6-21
Comparison of the Future Value of an Ordinary Annuity with an Annuity Due

In this example, the cash flows from the annuity due come exactly one period earlier than for an ordinary annuity. As a result, the future value of the annuity due factor is exactly 12% higher than the ordinary annuity factor. For example, the value of an ordinary annuity factor at the end of period one at 12% is 1.00000, whereas for an annuity due it is 1.12000.
To find the future value of an annuity due factor, multiply the future value of an ordinary annuity factor by 1 plus the interest rate. For example, to determine the future value of an annuity due interest factor for 5 periods at 12% compound interest, simply multiply the future value of an ordinary annuity interest factor for 5 periods (6.35285), by one plus the interest rate (1 + .12), to arrive at 7.11519 (6.35285 × 1.12).
To illustrate the use of the ordinary annuity tables in converting to an annuity due, assume that Erin Berge plans to deposit £800 a year on each birthday of her son Venden. She makes the first deposit on his tenth birthday, at 6% interest compounded annually. Erin wants to know the amount she will have accumulated for college expenses by her son's eighteenth birthday.
If the first deposit occurs on Venden's tenth birthday, Erin will make a total of 8 deposits over the life of the annuity (assume no deposit on the eighteenth birthday), as shown in Illustration 6-22. Because all the deposits are made at the beginning of the periods, they represent an annuity due.
ILLUSTRATION 6-22
Annuity Due Time Diagram

Referring to the “future value of an ordinary annuity of 1” table for 8 periods at 6%, Erin finds a factor of 9.89747. She then multiplies this factor by (1 + .06) to arrive at the future value of an annuity due factor. As a result, the accumulated value on Venden's eighteenth birthday is £8,393.05, as calculated in Illustration 6-23.
ILLUSTRATION 6-23
Computation of Accumulated Value of Annuity Due

Depending on the college he chooses, Venden may have enough to finance only part of his first year of school.
Examples of Future Value of Annuity Problems
The foregoing annuity examples relied on three known values—amount of each rent, interest rate, and number of periods. Using these values enables us to determine the unknown fourth value, future value.
The first two future value problems we present illustrate the computations of (1) the amount of the rents and (2) the number of rents. The third problem illustrates the computation of the future value of an annuity due.
Computation of Rent
Assume that you plan to accumulate CHF14,000 for a down payment on a condominium apartment 5 years from now. For the next 5 years, you earn an annual return of 8% compounded semiannually. How much should you deposit at the end of each 6-month period?
The CHF14,000 is the future value of 10 (5 × 2) semiannual end-of-period payments of an unknown amount, at an interest rate of 4% (8% ÷ 2). Illustration 6-24 depicts this problem as a time diagram.
ILLUSTRATION 6-24
Future Value of Ordinary Annuity Time Diagram (n = 10, i = 4%)

Using the formula for the future value of an ordinary annuity, you determine the amount of each rent as follows.

Thus, you must make 10 semiannual deposits of CHF1,166.07 each in order to accumulate CHF14,000 for your down payment.
Computation of the Number of Periodic Rents
Suppose that a company's goal is to accumulate $117,332 by making periodic deposits of $20,000 at the end of each year, which will earn 8% compounded annually while accumulating. How many deposits must it make?
The $117,332 represents the future value of n(?) $20,000 deposits, at an 8% annual rate of interest. Illustration 6-25 depicts this problem in a time diagram.
ILLUSTRATION 6-25
Future Value of Ordinary Annuity Time Diagram, to Solve for Unknown Number of Periods

Using the future value of an ordinary annuity formula, the company obtains the following factor.
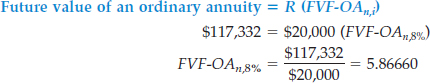
Use Table 6-3 and read down the 8% column to find 5.86660 in the 5-period row. Thus, the company must make five deposits of $20,000 each.
Computation of the Future Value
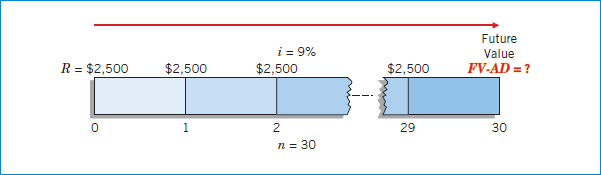
To create his retirement fund, Walter Goodwrench, a mechanic, now works weekends. Mr. Goodwrench deposits $2,500 today in a savings account that earns 9% interest. He plans to deposit $2,500 every year for a total of 30 years. How much cash will Mr. Goodwrench accumulate in his retirement savings account, when he retires in 30 years? Illustration 6-26 depicts this problem in a time diagram.
ILLUSTRATION 6-26
Future Value Annuity Due Time Diagram (n = 30, i = 9%)
Using the “future value of an ordinary annuity of 1” table, Mr. Goodwrench computes the solution as shown in Illustration 6-27.
ILLUSTRATION 6-27
Computation of Accumulated Value of an Annuity Due

Present Value of an Ordinary Annuity
![]() LEARNING OBJECTIVE
LEARNING OBJECTIVE
Solve present value of ordinary and annuity due problems.
The present value of an annuity is the single sum that, if invested at compound interest now, would provide for an annuity (a series of withdrawals) for a certain number of future periods. In other words, the present value of an ordinary annuity is the present value of a series of equal rents, to be withdrawn at equal intervals.
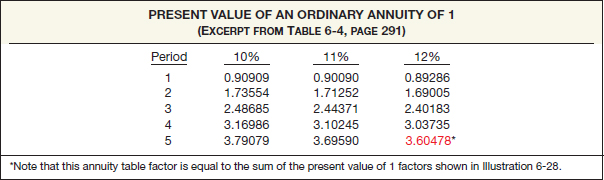
One approach to finding the present value of an annuity determines the present value of each of the rents in the series and then totals their individual present values. For example, we may view an annuity of $1, to be received at the end of each of 5 periods, as separate amounts. We then compute each present value using the table of present values (see pages 286–287), assuming an interest rate of 12%. Illustration 6-28 shows this approach.
ILLUSTRATION 6-28
Solving for the Present Value of an Ordinary Annuity

This computation tells us that if we invest the single sum of $3.60 today at 12% interest for 5 periods, we will be able to withdraw $1 at the end of each period for 5 periods. We can summarize this cumbersome procedure by the following formula.
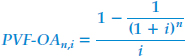
The expression PVF-OAn,i refers to the present value of an ordinary annuity of 1 factor for n periods at i interest. Ordinary annuity tables base present values on this formula. Illustration 6-29 shows an excerpt from such a table.
ILLUSTRATION 6-29
Excerpt from Table 6-4
The general formula for the present value of any ordinary annuity is as follows.
![]()
where
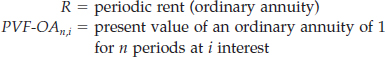
To illustrate with an example, what is the present value of rental receipts of $6,000 each, to be received at the end of each of the next 5 years when discounted at 12%? This problem may be time-diagrammed and solved as shown in Illustration 6-30.
ILLUSTRATION 6-30
Present Value of Ordinary Annuity Time Diagram

The formula for this calculation is as shown below.

The present value of the 5 ordinary annuity rental receipts of $6,000 each is $21,628.68. To determine the present value of the ordinary annuity factor 3.60478, use a financial calculator or read the appropriate table, in this case Table 6-4 (12% column, 5-period row).
What do the numbers mean? UP IN SMOKE
Time value of money concepts also can be relevant to public policy debates. For example, many governments must evaluate the financial cost-benefit of selling to a private operator the future cash flows associated with government-run services, such as toll roads and bridges. In these cases, the policy-maker must estimate the present value of the future cash flows in determining the price for selling the rights. In another example, some governmental entities had to determine how to receive the payments from tobacco companies as settlement for a national lawsuit against the companies for the healthcare costs of smoking.
In one situation, a governmental entity was due to collect 25 years of payments totaling $5.6 billion. The government could wait to collect the payments, or it could sell the payments to an investment bank (a process called securitization). If it were to sell the payments, it would receive a lump-sum payment today of $1.26 billion. Is this a good deal for this governmental entity? Assuming a discount rate of 8% and that the payments will be received in equal amounts (e.g., an annuity), the present value of the tobacco payment is:

Why would the government be willing to take just $1.26 billion today for an annuity whose present value is almost twice that amount? One reason is that the governmental entity was facing a hole in its budget that could be plugged in part by the lump-sum payment. Also, some believed that the risk of not getting paid by the tobacco companies in the future makes it prudent to get the money earlier.
If this latter reason has merit, then the present value computation above should have been based on a higher interest rate. Assuming a discount rate of 15%, the present value of the annuity is $1.448 billion ($5.6 billion ÷ 25 = $224 million; $224 million × 6.46415), which is much closer to the lump-sum payment offered to the governmental entity.
Present Value of an Annuity Due
In our discussion of the present value of an ordinary annuity, we discounted the final rent based on the number of rent periods. In determining the present value of an annuity due, there is always one fewer discount period. Illustration 6-31 shows this distinction.
ILLUSTRATION 6-31
Comparison of Present Value of an Ordinary Annuity with an Annuity Due
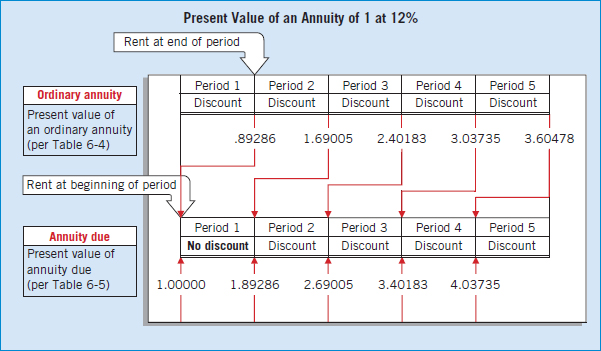
Because each cash flow comes exactly one period sooner in the present value of the annuity due, the present value of the cash flows is exactly 12% higher than the present value of an ordinary annuity. Thus, to find the present value of an annuity due factor, multiply the present value of an ordinary annuity factor by 1 plus the interest rate (that is, 1 + i).
To determine the present value of an annuity due interest factor for 5 periods at 12% interest, take the present value of an ordinary annuity for 5 periods at 12% interest (3.60478) and multiply it by 1.12 to arrive at the present value of an annuity due, 4.03735 (3.60478 × 1.12). We provide present value of annuity due factors in Table 6-5.
To illustrate, Space Odyssey, Inc., rents a communications satellite for 4 years with annual rental payments of $4.8 million to be made at the beginning of each year. If the relevant annual interest rate is 11%, what is the present value of the rental obligations? Illustration 6-32 shows the company's time diagram for this problem.
ILLUSTRATION 6-32
Present Value of Annuity Due Time Diagram (n = 4, i = 11%)

Illustration 6-33 shows the computations to solve this problem.
ILLUSTRATION 6-33
Computation of Present Value of an Annuity Due

Using Table 6-5 also locates the desired factor 3.44371 and computes the present value of the lease payments to be $16,529,808. (The difference in computations is due to rounding.)
Examples of Present Value of Annuity Problems
In the following three examples, we demonstrate the computation of (1) the present value, (2) the interest rate, and (3) the amount of each rent.
Computation of the Present Value of an Ordinary Annuity
You have just won a lottery totaling $4,000,000. You learn that you will receive a check in the amount of $200,000 at the end of each of the next 20 years. What amount have you really won? That is, what is the present value of the $200,000 checks you will receive over the next 20 years? Illustration 6-34 shows a time diagram of this enviable situation (assuming an appropriate interest rate of 10%).
You calculate the present value as follows.

ILLUSTRATION 6-34
Time Diagram to Solve for Present Value of Lottery Payments
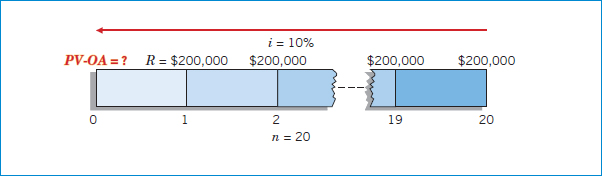
As a result, if the state deposits $1,702,712 now and earns 10% interest, it can withdraw $200,000 a year for 20 years to pay you the $4,000,000.
Computation of the Interest Rate
Many shoppers use credit cards to make purchases. When you receive the statement for payment, you may pay the total amount due or you may pay the balance in a certain number of payments. For example, assume you receive a statement from MasterCard with a balance due of €528.77. You may pay it off in 12 equal monthly payments of €50 each, with the first payment due one month from now. What rate of interest would you be paying?
The €528.77 represents the present value of the 12 payments of €50 each at an unknown rate of interest. The time diagram in Illustration 6-35 depicts this situation.
ILLUSTRATION 6-35
Time Diagram to Solve for Effective-Interest Rate on Loan

You calculate the rate as follows.

Referring to Table 6-4 and reading across the 12-period row, you find 10.57534 in the 2% column. Since 2% is a monthly rate, the nominal annual rate of interest is 24% (12 × 2%). The effective annual rate is 26.82% [(1 + .02)12 − 1]. Obviously, you are better off paying the entire bill now if possible.
Computation of a Periodic Rent
Juan and Marcia Perez have saved $36,000 to finance their daughter Maria's college education. They deposited the money in the Santos Bank, where it earns 4% interest compounded semiannually. What equal amounts can their daughter withdraw at the end of every 6 months during her 4 college years, without exhausting the fund? Illustration 6-36 (on page 262) shows a time diagram of this situation.
ILLUSTRATION 6-36
Time Diagram for Ordinary Annuity for a College Fund
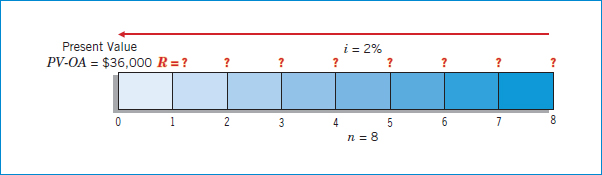
Determining the answer by simply dividing $36,000 by 8 withdrawals is wrong. Why? Because that ignores the interest earned on the money remaining on deposit. Maria must consider that interest is compounded semiannually at 2% (4% ÷ 2) for 8 periods (4 years × 2). Thus, using the same present value of an ordinary annuity formula, she determines the amount of each withdrawal that she can make as follows.
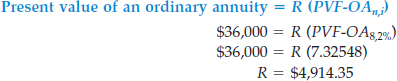
MORE COMPLEX SITUATIONS
LEARNING OBJECTIVE ![]()
Solve present value problems related to deferred annuities and bonds.
Solving time value problems often requires using more than one table. For example, a business problem may need computations of both present value of a single sum and present value of an annuity. Two such common situations are:
1. Deferred annuities.
2. Bond problems.
Deferred Annuities
A deferred annuity is an annuity in which the rents begin after a specified number of periods. A deferred annuity does not begin to produce rents until two or more periods have expired. For example, “an ordinary annuity of six annual rents deferred 4 years” means that no rents will occur during the first 4 years and that the first of the six rents will occur at the end of the fifth year. “An annuity due of six annual rents deferred 4 years” means that no rents will occur during the first 4 years and that the first of six rents will occur at the beginning of the fifth year.
Future Value of a Deferred Annuity
Computing the future value of a deferred annuity is relatively straightforward. Because there is no accumulation or investment on which interest may accrue, the future value of a deferred annuity is the same as the future value of an annuity not deferred. That is, computing the future value simply ignores the deferred period.
To illustrate, assume that Sutton Corporation plans to purchase a land site in 6 years for the construction of its new corporate headquarters. Because of cash flow problems, Sutton budgets deposits of $80,000 on which it expects to earn 5% annually, only at the end of the fourth, fifth, and sixth periods. What future value will Sutton have accumulated at the end of the sixth year? Illustration 6-37 shows a time diagram of this situation.
ILLUSTRATION 6-37
Time Diagram for Future Value of Deferred Annuity
Sutton determines the value accumulated by using the standard formula for the future value of an ordinary annuity:

Present Value of a Deferred Annuity
Computing the present value of a deferred annuity must recognize the interest that accrues on the original investment during the deferral period.
To compute the present value of a deferred annuity, we compute the present value of an ordinary annuity of 1 as if the rents had occurred for the entire period. We then subtract the present value of rents that were not received during the deferral period. We are left with the present value of the rents actually received subsequent to the deferral period.
To illustrate, Bob Bender has developed and copyrighted tutorial software for students in advanced accounting. He agrees to sell the copyright to Campus Micro Systems for 6 annual payments of $5,000 each. The payments will begin 5 years from today. Given an annual interest rate of 8%, what is the present value of the 6 payments?
This situation is an ordinary annuity of 6 payments deferred 4 periods. The time diagram in Illustration 6-38 depicts this sales agreement.
ILLUSTRATION 6-38
Time Diagram for Present Value of Deferred Annuity

Two options are available to solve this problem. The first is to use only Table 6-4, as shown in Illustration 6-39.
ILLUSTRATION 6-39
Computation of the Present Value of a Deferred Annuity

The subtraction of the present value of an annuity of 1 for the deferred periods eliminates the non-existent rents during the deferral period. It converts the present value of an ordinary annuity of $1.00 for 10 periods to the present value of 6 rents of $1.00, deferred 4 periods.
Alternatively, Bender can use both Table 6-2 and Table 6-4 to compute the present value of the 6 rents. He can first discount the annuity 6 periods. However, because the annuity is deferred 4 periods, he must treat the present value of the annuity as a future amount to be discounted another 4 periods. The time diagram in Illustration 6-40 depicts this two-step process.
ILLUSTRATION 6-40
Time Diagram for Present Value of Deferred Annuity (2-Step Process)

Calculation using formulas would be done in two steps, as follows.

The present value of $16,989.78 computed above is the same as in Illustration 6-39 although computed differently. (The $0.03 difference is due to rounding.)
Valuation of Long-Term Bonds
A long-term bond produces two cash flows: (1) periodic interest payments during the life of the bond, and (2) the principal (face value) paid at maturity. At the date of issue, bond buyers determine the present value of these two cash flows using the market rate of interest.
The periodic interest payments represent an annuity. The principal represents a single-sum problem. The current market value of the bonds is the combined present values of the interest annuity and the principal amount.
To illustrate, Alltech Corporation on January 1, 2015, issues $100,000 of 9% bonds due in 5 years with interest payable annually at year-end. The current market rate of interest for bonds of similar risk is 11%. What will the buyers pay for this bond issue?
The time diagram in Illustration 6-41 depicts both cash flows.
ILLUSTRATION 6-41
Time Diagram to Solve for Bond Valuation

Alltech computes the present value of the two cash flows by discounting at 11% as follows.
ILLUSTRATION 6-42
Computation of the Present Value of an Interest-Bearing Bond

By paying $92,608.10 at date of issue, the buyers of the bonds will realize an effective yield of 11% over the 5-year term of the bonds. This is true because Alltech discounted the cash flows at 11%.
Effective-Interest Method of Amortization of Bond Discount or Premium
In the previous example (Illustration 6-42), Alltech Corporation issued bonds at a discount, computed as follows.
ILLUSTRATION 6-43
Computation of Bond Discount

Alltech amortizes (writes off to interest expense) the amount of this discount over the life of the bond issue.
The procedure for amortization of a discount or premium is the effective-interest method. Under the effective-interest method:
1. The company issuing the bond first computes bond interest expense by multiplying the carrying value of the bonds at the beginning of the period by the effective-interest rate.
2. The company then determines the bond discount or premium amortization by comparing the bond interest expense with the interest to be paid.
Illustration 6-44 depicts the computation of bond amortization.
ILLUSTRATION 6-44
Amortization Computation

The effective-interest method produces a periodic interest expense equal to a constant percentage of the carrying value of the bonds. Since the percentage used is the effective rate of interest incurred by the borrower at the time of issuance, the effective-interest method results in matching expenses with revenues.
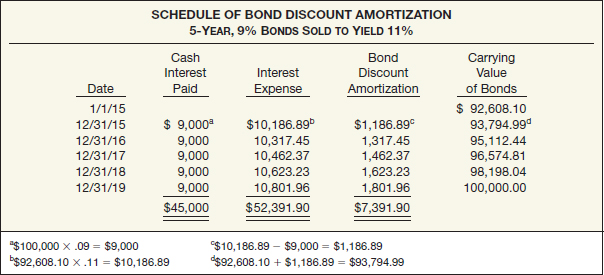
We can use the data from the Alltech Corporation example to illustrate the effective-interest method of amortization. Alltech issued $100,000 face value of bonds at a discount of $7,391.90, resulting in a carrying value of $92,608.10. Illustration 6-45 shows the effective-interest amortization schedule for Alltech's bonds.
ILLUSTRATION 6-45
Effective-Interest Amortization Schedule
We use the amortization schedule illustrated above for note and bond transactions in Chapters 7 and 14.
PRESENT VALUE MEASUREMENT
LEARNING OBJECTIVE ![]()
Apply expected cash flows to present value measurement.
In the past, most accounting calculations of present value relied on the most likely cash flow amount. IFRS 13 explains in detail a different approach called the expected cash flow approach. [7] It uses a range of cash flows and incorporates the probabilities of those cash flows to provide a more relevant measurement of present value.
To illustrate the expected cash flow model, assume that there is a 30% probability that future cash flows will be $100, a 50% probability that they will be $200, and a 20% probability that they will be $300. In this case, the expected cash flow would be $190 [($100 × 0.3) + ($200 × 0.5) + ($300 × 0.2)]. Traditional present value approaches would use the most likely estimate ($200). However, that estimate fails to consider the different probabilities of the possible cash flows.
Choosing an Appropriate Interest Rate
After determining expected cash flows, a company must then use the proper interest rate to discount the cash flows. The interest rate used for this purpose has three components:
THREE COMPONENTS OF INTEREST
1. PURE RATE OF INTEREST (2%–4%). This would be the amount a lender would charge if there were no possibilities of default and no expectation of inflation.
2. EXPECTED INFLATION RATE OF INTEREST (0%–?). Lenders recognize that in an inflationary economy, they are being paid back with less valuable dollars. As a result, they increase their interest rate to compensate for this loss in purchasing power. When inflationary expectations are high, interest rates are high.
3. CREDIT RISK RATE OF INTEREST (0%–5%). The government has little or no credit risk (i.e., risk of non-payment) when it issues bonds. A business enterprise, however, depending upon its financial stability, profitability, and liquidity, can have a low or a high credit risk.
The IASB takes the position that after computing the expected cash flows, a company should discount those cash flows by the risk-free rate of return. That rate is defined as the pure rate of return plus the expected inflation rate. The Board notes that the expected cash flow framework adjusts for credit risk because it incorporates the probability of receipt or payment into the computation of expected cash flows. Therefore, the rate used to discount the expected cash flows should consider only the pure rate of interest and the inflation rate.6
Example of Expected Cash Flow
To illustrate, assume that Juno's Appliance Outlet offers a 2-year warranty on all products sold. In 2015, Juno's Appliance sold $250,000 of a particular type of clothes dryer. Juno's Appliance entered into an agreement with Lorenzo's Repair to perform all warranty service on the dryers sold in 2015. To determine the warranty expense to record in 2015 and the amount of warranty liability to record on the December 31, 2015, statement of financial position, Juno's Appliance must measure the fair value of the agreement. Since there is not a ready market for these warranty contracts, Juno's Appliance uses expected cash flow techniques to value the warranty obligation.
Based on prior warranty experience, Juno's Appliance estimates the expected cash outflows associated with the dryers sold in 2015, as shown in Illustration 6-46 (on page 268).
ILLUSTRATION 6-46
Expected Cash Outflows—Warranties
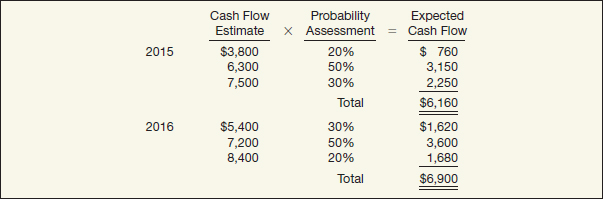
Applying expected cash flow concepts to these data, Juno's Appliance estimates warranty cash outflows of $6,160 in 2015 and $6,900 in 2016.
Illustration 6-47 shows the present value of these cash flows, assuming a risk-free rate of 5% and cash flows occurring at the end of the year.7
ILLUSTRATION 6-47
Present Value of Cash Flows

KEY TERMS
annuity, 252
annuity due, 252
compound interest, 242
deferred annuity, 262
discounting, 247
effective-interest method, 265
effective yield, 245
expected cash flow approach, 266
face rate, 245
future value, 246
future value of an annuity, 252
interest, 241
nominal rate, 245
ordinary annuity, 252
present value, 246
principal, 241
risk-free rate of return, 267
simple interest, 242
stated rate, 245
time value of money, 240
SUMMARY OF LEARNING OBJECTIVES
![]() Identify accounting topics where the time value of money is relevant. Some of the applications of present value–based measurements to accounting topics are (1) notes, (2) leases, (3) pensions and other postretirement benefits, (4) long-term assets, (5) sinking funds, (6) business combinations, (7) disclosures, and (8) installment contracts.
Identify accounting topics where the time value of money is relevant. Some of the applications of present value–based measurements to accounting topics are (1) notes, (2) leases, (3) pensions and other postretirement benefits, (4) long-term assets, (5) sinking funds, (6) business combinations, (7) disclosures, and (8) installment contracts.
![]() Distinguish between simple and compound interest. See items 1 and 2 in the Fundamental Concepts on page 269.
Distinguish between simple and compound interest. See items 1 and 2 in the Fundamental Concepts on page 269.
![]() Use appropriate compound interest tables. In order to identify which of the five compound interest tables to use, determine whether you are solving for (1) the future value of a single sum, (2) the present value of a single sum, (3) the future value of a series of sums (an annuity), or (4) the present value of a series of sums (an annuity). In addition, when a series of sums (an annuity) is involved, identify whether these sums are received or paid (1) at the beginning of each period (annuity due) or (2) at the end of each period (ordinary annuity).
Use appropriate compound interest tables. In order to identify which of the five compound interest tables to use, determine whether you are solving for (1) the future value of a single sum, (2) the present value of a single sum, (3) the future value of a series of sums (an annuity), or (4) the present value of a series of sums (an annuity). In addition, when a series of sums (an annuity) is involved, identify whether these sums are received or paid (1) at the beginning of each period (annuity due) or (2) at the end of each period (ordinary annuity).
![]() Identify variables fundamental to solving interest problems. The following four variables are fundamental to all compound interest problems. (1) Rate of interest: unless otherwise stated, an annual rate, adjusted to reflect the length of the compounding period if less than a year. (2) Number of time periods: the number of compounding periods (a period may be equal to or less than a year). (3) Future value: the value at a future date of a given sum or sums invested assuming compound interest. (4) Present value: the value now (present time) of a future sum or sums discounted assuming compound interest.
Identify variables fundamental to solving interest problems. The following four variables are fundamental to all compound interest problems. (1) Rate of interest: unless otherwise stated, an annual rate, adjusted to reflect the length of the compounding period if less than a year. (2) Number of time periods: the number of compounding periods (a period may be equal to or less than a year). (3) Future value: the value at a future date of a given sum or sums invested assuming compound interest. (4) Present value: the value now (present time) of a future sum or sums discounted assuming compound interest.
![]() Solve future and present value of 1 problems. See items 5(a) and 6(a) in the Fundamental Concepts below and on page 270.
Solve future and present value of 1 problems. See items 5(a) and 6(a) in the Fundamental Concepts below and on page 270.
![]() Solve future value of ordinary and annuity due problems. See item 5(b) in the Fundamental Concepts on page 270.
Solve future value of ordinary and annuity due problems. See item 5(b) in the Fundamental Concepts on page 270.
![]() Solve present value of ordinary and annuity due problems. See item 6(b) in the Fundamental Concepts on page 270.
Solve present value of ordinary and annuity due problems. See item 6(b) in the Fundamental Concepts on page 270.
![]() Solve present value problems related to deferred annuities and bonds. Deferred annuities are annuities in which rents begin after a specified number of periods. The future value of a deferred annuity is computed the same as the future value of an annuity not deferred. To find the present value of a deferred annuity, compute the present value of an ordinary annuity of 1 as if the rents had occurred for the entire period, and then subtract the present value of rents not received during the deferral period. The current market value of bonds combines the present values of the interest annuity and the principal amount.
Solve present value problems related to deferred annuities and bonds. Deferred annuities are annuities in which rents begin after a specified number of periods. The future value of a deferred annuity is computed the same as the future value of an annuity not deferred. To find the present value of a deferred annuity, compute the present value of an ordinary annuity of 1 as if the rents had occurred for the entire period, and then subtract the present value of rents not received during the deferral period. The current market value of bonds combines the present values of the interest annuity and the principal amount.
![]() Apply expected cash flows to present value measurement. The expected cash flow approach uses a range of cash flows and the probabilities of those cash flows to provide the most likely estimate of expected cash flows. The proper interest rate used to discount the cash flows is the risk-free rate of return.
Apply expected cash flows to present value measurement. The expected cash flow approach uses a range of cash flows and the probabilities of those cash flows to provide the most likely estimate of expected cash flows. The proper interest rate used to discount the cash flows is the risk-free rate of return.
FUNDAMENTAL CONCEPTS
1. SIMPLE INTEREST. Interest on principal only, regardless of interest that may have accrued in the past.
2. COMPOUND INTEREST. Interest accrues on the unpaid interest of past periods as well as on the principal.
3. RATE OF INTEREST. Interest is usually expressed as an annual rate, but when the compounding period is shorter than one year, the interest rate for the shorter period must be determined.
4. ANNUITY. A series of payments or receipts (called rents) that occur at equal intervals of time. Types of annuities:
(a) Ordinary Annuity. Each rent is payable (receivable) at the end of the period.
(b) Annuity Due. Each rent is payable (receivable) at the beginning of the period.
5. FUTURE VALUE. Value at a later date of a single sum that is invested at compound interest.
(a) Future Value of 1 (or value of a single sum). The future value of 1 (or a single given sum), FV, at the end of n periods at i compound interest rate (Table 6-1).
(b) Future Value of an Annuity. The future value of a series of rents invested at compound interest. In other words, the accumulated total that results from a series of equal deposits at regular intervals invested at compound interest. Both deposits and interest increase the accumulation.
6. PRESENT VALUE. The value at an earlier date (usually now) of a given future sum discounted at compound interest.
(a) Present Value of 1 (or present value of a single sum). The present value (worth) of 1 (or a given sum), due n periods hence, discounted at i compound interest (Table 6-2).
(b) Present Value of an Annuity. The present value (worth) of a series of rents discounted at compound interest. In other words, it is the sum when invested at compound interest that will permit a series of equal withdrawals at regular intervals.
(1) Present Value of an Ordinary Annuity. The value now of 1 to be received or paid at the end of each period (rents) for n periods, discounted at i compound interest (Table 6-4).
(2) Present Value of an Annuity Due. The value now of 1 to be received or paid at the beginning of each period (rents) for n periods, discounted at i compound interest (Table 6-5). To use Table 6-4 for an annuity due, apply this formula.

Authoritative Literature References
[1] International Accounting Standard 36, Impairment of Assets (London, U.K.: International Accounting Standards Committee Foundation, March 2004), Appendix A and International Financial Reporting Standard 7, Financial Instruments: Disclosures (London, U.K.: International Accounting Standards Committee Foundation, 2005), par. 27.
[2] International Accounting Standard 39, Financial Instruments: Recognition and Measurement (London, U.K.: International Accounting Standards Committee Foundation, 2003).
[3] International Accounting Standard 17, Leases (London, U.K.: International Accounting Standards Committee Foundation, 2003).
[4] International Accounting Standard 19, Employee Benefits (London, U.K.: International Accounting Standards Committee Foundation, 2001).
[5] International Accounting Standard 36, Impairment of Assets (London, U.K.: International Accounting Standards Committee Foundation, 2004).
[6] International Financial Reporting Standard 2, Share-Based Payment (London, U.K.: International Accounting Standards Committee Foundation, 2004).
[7] International Financial Reporting Standard 13, Fair Value Measurement (London, U.K.: International Accounting Standards Committee Foundation, 2011), paras. B12–B30; and International Accounting Standard 36, Impairment of Assets (London, U.K.: International Accounting Standards Committee Foundation, 2004), Appendix A.
[8] International Financial Reporting Standard 13, Fair Value Measurement (London, U.K.: International Accounting Standards Committee Foundation, 2011), paras. B14–B19; and International Accounting Standard 36, Impairment of Assets (London, U.K.: International Accounting Standards Committee Foundation, 2004), par. A3.
1. What is the time value of money? Why should accountants have an understanding of compound interest, annuities, and present value concepts?
2. Identify three situations in which accounting measures are based on present values. Do these present value applications involve single sums or annuities, or both single sums and annuities? Explain.
3. What is the nature of interest? Distinguish between “simple interest” and “compound interest.”
4. What are the components of an interest rate? Why is it important for accountants to understand these components?
5. Presented below are a number of values taken from compound interest tables involving the same number of periods and the same rate of interest. Indicate what each of these four values represents.
- (a) 6.71008
- (b) 2.15892
- (c) .46319
- (d) 14.48656
6. Jose Oliva is considering two investment options for a R$1,500 gift he received for graduation. Both investments have 8% annual interest rates. One offers quarterly compounding; the other compounds on a semiannual basis. Which investment should he choose? Why?
7. Regina Henry deposited $20,000 in a money market certificate that provides interest of 10% compounded quarterly if the amount is maintained for 3 years. How much will Regina Henry have at the end of 3 years?
8. Will Smith will receive $80,000 on December 31, 2020 (5 years from now), from a trust fund established by his father. Assuming the appropriate interest rate for discounting is 12% (compounded semiannually), what is the present value of this amount today?
9. What are the primary characteristics of an annuity? Differentiate between an “ordinary annuity” and an “annuity due.”
10. Kehoe, Inc. owes €40,000 to Ritter Company. How much would Kehoe have to pay each year if the debt is retired through four equal payments (made at the end of the year), given an interest rate on the debt of 12%? (Round to two decimal places.)
11. The Wangs are planning for a retirement home. They estimate they will need ¥20,000,000 4 years from now to purchase this home. Assuming an interest rate of 10%, what amount must be deposited at the end of each of the 4 years to fund the home price? (Round to two decimal places.)
12. Assume the same situation as in Question 11, except that the four equal amounts are deposited at the beginning of the period rather than at the end. In this case, what amount must be deposited at the beginning of each period? (Round to two decimals.)
13. Explain how the future value of an ordinary annuity interest table is converted to the future value of an annuity due interest table.
14. Explain how the present value of an ordinary annuity interest table is converted to the present value of an annuity due interest table.
15. In a book named Treasure, the reader has to figure out where a 2.2 pound, 24 kt gold horse has been buried. If the horse is found, a prize of $25,000 a year for 20 years is provided. The actual cost to the publisher to purchase an annuity to pay for the prize is $245,000. What interest rate (to the nearest percent) was used to determine the amount of the annuity? (Assume end-of-year payments.)
16. Verma Enterprises leases property to Pandey, Inc. Because Pandey, Inc. is experiencing financial difficulty, Verma agrees to receive five rents of £20,000 at the end of each year, with the rents deferred 3 years. What is the present value of the five rents discounted at 12%?
17. Answer the following questions.
- (a) On May 1, 2015, Goldberg Company sold some machinery to Newlin Company on an installment contract basis. The contract required five equal annual payments, with the first payment due on May 1, 2015. What present value concept is appropriate for this situation?
- (b) On June 1, 2015, Lin Inc. purchased a new machine that it does not have to pay for until May 1, 2017. The total payment on May 1, 2017, will include both principal and interest. Assuming interest at a 12% rate, the cost of the machine would be the total payment multiplied by what time value of money concept?
- (c) Guha Company wishes to know how much money it will have available in 5 years if five equal amounts of $35,000 are invested, with the first amount invested immediately. What interest table is appropriate for this situation?
- (d) Jane Lindholm invests in a “jumbo” $200,000, 3-year certificate of deposit at ING Bank. What table would be used to determine the amount accumulated at the end of 3 years?
18. Recently, Glenda Estes was interested in purchasing a Honda Acura. The salesperson indicated that the price of the car was either R$27,600 cash or R$6,900 at the end of each of 5 years. Compute the effective-interest rate to the nearest percent that Glenda would pay if she chooses to make the five annual payments.
19. Recently, property/casualty insurance companies have been criticized because they reserve for the total loss as much as 5 years before it may happen. The taxing authority has joined the debate because it says the full reserve is unfair from a taxation viewpoint. What do you believe is the taxing authority's position?
![]() BE6-1 Victor Romano invested $15,000 today in a fund that earns 8% compounded annually. To what amount will the investment grow in 3 years? To what amount would the investment grow in 3 years if the fund earns 8% annual interest compounded semiannually?
BE6-1 Victor Romano invested $15,000 today in a fund that earns 8% compounded annually. To what amount will the investment grow in 3 years? To what amount would the investment grow in 3 years if the fund earns 8% annual interest compounded semiannually?
![]() BE6-2 Tony Bautista needs R$25,000 in 4 years. What amount must he invest today if his investment earns 12% compounded annually? What amount must he invest if his investment earns 12% annual interest compounded quarterly?
BE6-2 Tony Bautista needs R$25,000 in 4 years. What amount must he invest today if his investment earns 12% compounded annually? What amount must he invest if his investment earns 12% annual interest compounded quarterly?
![]() BE6-3 Candice Willis will invest €30,000 today. She needs €150,000 in 21 years. What annual interest rate must she earn?
BE6-3 Candice Willis will invest €30,000 today. She needs €150,000 in 21 years. What annual interest rate must she earn?
![]() BE6-4 Bo Newman will invest $10,000 today in a fund that earns 5% annual interest. How many years will it take for the fund to grow to $17,100?
BE6-4 Bo Newman will invest $10,000 today in a fund that earns 5% annual interest. How many years will it take for the fund to grow to $17,100?
![]() BE6-5 Sally Medavoy will invest €8,000 a year for 20 years in a fund that will earn 12% annual interest. If the first payment into the fund occurs today, what amount will be in the fund in 20 years? If the first payment occurs at year-end, what amount will be in the fund in 20 years?
BE6-5 Sally Medavoy will invest €8,000 a year for 20 years in a fund that will earn 12% annual interest. If the first payment into the fund occurs today, what amount will be in the fund in 20 years? If the first payment occurs at year-end, what amount will be in the fund in 20 years?
![]() BE6-6 Steve Madison needs $250,000 in 10 years. How much must he invest at the end of each year, at 11% interest, to meet his needs?
BE6-6 Steve Madison needs $250,000 in 10 years. How much must he invest at the end of each year, at 11% interest, to meet his needs?
![]() BE6-7 Jose Garcia's lifelong dream is to own a fishing boat to use in his retirement. Jose has recently come into an inheritance of R$400,000. He estimates that the boat he wants will cost R$300,000 when he retires in 5 years. How much of his inheritance must he invest at an annual rate of 12% (compounded annually) to buy the boat at retirement?
BE6-7 Jose Garcia's lifelong dream is to own a fishing boat to use in his retirement. Jose has recently come into an inheritance of R$400,000. He estimates that the boat he wants will cost R$300,000 when he retires in 5 years. How much of his inheritance must he invest at an annual rate of 12% (compounded annually) to buy the boat at retirement?
![]() BE6-8 Refer to the data in BE6-7. Assuming quarterly compounding of amounts invested at 12%, how much of Jose Garcia's inheritance must be invested to have enough at retirement to buy the boat?
BE6-8 Refer to the data in BE6-7. Assuming quarterly compounding of amounts invested at 12%, how much of Jose Garcia's inheritance must be invested to have enough at retirement to buy the boat?
![]() BE6-9 Morgan Freeman is investing $16,380 at the end of each year in a fund that earns 10% interest. In how many years will the fund be at $100,000?
BE6-9 Morgan Freeman is investing $16,380 at the end of each year in a fund that earns 10% interest. In how many years will the fund be at $100,000?
![]() BE6-10 Henry Quincy wants to withdraw £30,000 each year for 10 years from a fund that earns 8% interest. How much must he invest today if the first withdrawal is at year-end? How much must he invest today if the first withdrawal takes place immediately?
BE6-10 Henry Quincy wants to withdraw £30,000 each year for 10 years from a fund that earns 8% interest. How much must he invest today if the first withdrawal is at year-end? How much must he invest today if the first withdrawal takes place immediately?
![]() BE6-11 Leon Tyler's VISA balance is $793.15. He may pay it off in 12 equal end-of-month payments of $75 each. What interest rate is Leon paying?
BE6-11 Leon Tyler's VISA balance is $793.15. He may pay it off in 12 equal end-of-month payments of $75 each. What interest rate is Leon paying?
![]() BE6-12 Maria Alvarez is investing $300,000 in a fund that earns 8% interest compounded annually. What equal amounts can Maria withdraw at the end of each of the next 20 years?
BE6-12 Maria Alvarez is investing $300,000 in a fund that earns 8% interest compounded annually. What equal amounts can Maria withdraw at the end of each of the next 20 years?
![]() BE6-13 Gomez Inc. will deposit $30,000 in a 12% fund at the end of each year for 8 years beginning December 31, 2015. What amount will be in the fund immediately after the last deposit?
BE6-13 Gomez Inc. will deposit $30,000 in a 12% fund at the end of each year for 8 years beginning December 31, 2015. What amount will be in the fund immediately after the last deposit?
![]() BE6-14 Liv Diaz wants to create a fund today that will enable her to withdraw R$25,000 per year for 8 years, with the first withdrawal to take place 5 years from today. If the fund earns 8% interest, how much must Liv invest today?
BE6-14 Liv Diaz wants to create a fund today that will enable her to withdraw R$25,000 per year for 8 years, with the first withdrawal to take place 5 years from today. If the fund earns 8% interest, how much must Liv invest today?
![]() BE6-15 Wong Inc. issues HK$2,000,000 of 7% bonds due in 10 years with interest payable at year-end. The current market rate of interest for bonds of similar risk is 8%. What amount will Wong receive when it issues the bonds (amounts in thousands)?
BE6-15 Wong Inc. issues HK$2,000,000 of 7% bonds due in 10 years with interest payable at year-end. The current market rate of interest for bonds of similar risk is 8%. What amount will Wong receive when it issues the bonds (amounts in thousands)?
![]() BE6-16 Zach Taylor is settling a £20,000 loan due today by making 6 equal annual payments of £4,727.53. Determine the interest rate on this loan if the payments begin one year after the loan is signed.
BE6-16 Zach Taylor is settling a £20,000 loan due today by making 6 equal annual payments of £4,727.53. Determine the interest rate on this loan if the payments begin one year after the loan is signed.
![]() BE6-17 Consider the loan in BE6-16. What payments must Zach Taylor make to settle the loan at the same interest rate but with the 6 payments beginning on the day the loan is signed?
BE6-17 Consider the loan in BE6-16. What payments must Zach Taylor make to settle the loan at the same interest rate but with the 6 payments beginning on the day the loan is signed?
(Interest rates are per annum unless otherwise indicated.)
![]() E6-1 (Using Interest Tables) For each of the following cases, indicate (a) to what rate columns, and (b) to what number of periods you would refer in looking up the interest factor.
E6-1 (Using Interest Tables) For each of the following cases, indicate (a) to what rate columns, and (b) to what number of periods you would refer in looking up the interest factor.
1. In a future value of 1 table
2. In a present value of an annuity of 1 table

![]() E6-2 (Simple and Compound Interest Computations) Sue Ang invests HK$30,000 at 8% annual interest, leaving the money invested without withdrawing any of the interest for 8 years. At the end of the 8 years, Sue withdraws the accumulated amount of money.
E6-2 (Simple and Compound Interest Computations) Sue Ang invests HK$30,000 at 8% annual interest, leaving the money invested without withdrawing any of the interest for 8 years. At the end of the 8 years, Sue withdraws the accumulated amount of money.
Instructions
(a) Compute the amount Sue would withdraw assuming the investment earns simple interest.
(b) Compute the amount Sue would withdraw assuming the investment earns interest compounded annually.
(c) Compute the amount Sue would withdraw assuming the investment earns interest compounded semiannually.
![]() E6-3 (Computation of Future Values and Present Values) Using the appropriate interest table, answer each of the following questions. (Each case is independent of the others.)
E6-3 (Computation of Future Values and Present Values) Using the appropriate interest table, answer each of the following questions. (Each case is independent of the others.)
(a) What is the future value of €9,000 at the end of 5 periods at 8% compounded interest?
(b) What is the present value of €9,000 due 8 periods hence, discounted at 11%?
(c) What is the future value of 15 periodic payments of €9,000 each made at the end of each period and compounded at 10%?
(d) What is the present value of €9,000 to be received at the end of each of 20 periods, discounted at 5% compound interest?
![]() E6-4 (Computation of Future Values and Present Values) Using the appropriate interest table, answer the following questions. (Each case is independent of the others.)
E6-4 (Computation of Future Values and Present Values) Using the appropriate interest table, answer the following questions. (Each case is independent of the others.)
(a) What is the future value of 20 periodic payments of $5,000 each made at the beginning of each period and compounded at 8%?
(b) What is the present value of $2,500 to be received at the beginning of each of 30 periods, discounted at 10% compound interest?
(c) What is the future value of 15 deposits of $2,000 each made at the beginning of each period and compounded at 10%? (Future value as of the end of the fifteenth period.)
(d) What is the present value of six receipts of $3,000 each received at the beginning of each period, discounted at 9% compounded interest?
![]() E6-5 (Computation of Present Value) Using the appropriate interest table, compute the present values of the following periodic amounts due at the end of the designated periods.
E6-5 (Computation of Present Value) Using the appropriate interest table, compute the present values of the following periodic amounts due at the end of the designated periods.
(a) £50,000 receivable at the end of each period for 8 periods compounded at 12%.
(b) £50,000 payments to be made at the end of each period for 16 periods at 9%.
(c) £50,000 payable at the end of the seventh, eighth, ninth, and tenth periods at 12%.
![]() E6-6 (Future Value and Present Value Problems) Presented below are three unrelated situations (amounts in thousands).
E6-6 (Future Value and Present Value Problems) Presented below are three unrelated situations (amounts in thousands).
(a) Li Chang Company recently signed a lease for a new office building, for a lease period of 10 years. Under the lease agreement, a security deposit of ¥1,200,000 is made, with the deposit to be returned at the expiration of the lease, with interest compounded at 10% per year. What amount will the company receive at the time the lease expires?
(b) Ron Wu Corporation, having recently issued a ![]() 20 million, 15-year bond issue, is committed to make annual sinking fund deposits of
20 million, 15-year bond issue, is committed to make annual sinking fund deposits of ![]() 620,000. The deposits are made on the last day of each year and yield a return of 10%. Will the fund at the end of 15 years be sufficient to retire the bonds? If not, what will the deficiency be?
620,000. The deposits are made on the last day of each year and yield a return of 10%. Will the fund at the end of 15 years be sufficient to retire the bonds? If not, what will the deficiency be?
(c) Under the terms of his salary agreement, president Juan Rivera has an option of receiving either an immediate bonus of R$40,000, or a deferred bonus of R$75,000 payable in 10 years. Ignoring tax considerations and assuming a relevant interest rate of 8%, which form of settlement should Rivera accept?
![]() E6-7 (Computation of Bond Prices) What would you pay for a $100,000 debenture bond that matures in 15 years and pays $10,000 a year in interest if you wanted to earn a yield of:
E6-7 (Computation of Bond Prices) What would you pay for a $100,000 debenture bond that matures in 15 years and pays $10,000 a year in interest if you wanted to earn a yield of:
![]()
![]() E6-8 (Computations for a Retirement Fund) Stephen Bosworth, a super salesman contemplating retirement on his fifty-fifth birthday, decides to create a fund on an 8% basis that will enable him to withdraw $25,000 per year on June 30, beginning in 2019 and continuing through 2022. To develop this fund, Stephen intends to make equal contributions on June 30 of each of the years 2015–2018.
E6-8 (Computations for a Retirement Fund) Stephen Bosworth, a super salesman contemplating retirement on his fifty-fifth birthday, decides to create a fund on an 8% basis that will enable him to withdraw $25,000 per year on June 30, beginning in 2019 and continuing through 2022. To develop this fund, Stephen intends to make equal contributions on June 30 of each of the years 2015–2018.
Instructions
(a) How much must the balance of the fund equal on June 30, 2018, in order for Stephen Bosworth to satisfy his objective?
(b) What are each of Stephen's contributions to the fund?
![]() E6-9 (Unknown Rate) Kross Company purchased a machine at a price of £100,000 by signing a note payable, which requires a single payment of £118,810 in 2 years. Assuming annual compounding of interest, what rate of interest is being paid on the loan?
E6-9 (Unknown Rate) Kross Company purchased a machine at a price of £100,000 by signing a note payable, which requires a single payment of £118,810 in 2 years. Assuming annual compounding of interest, what rate of interest is being paid on the loan?
![]() E6-10 (Unknown Periods and Unknown Interest Rate) Consider the following independent situations.
E6-10 (Unknown Periods and Unknown Interest Rate) Consider the following independent situations.
(a) R. Chopra wishes to become a millionaire. His money market fund has a balance of $148,644 and has a guaranteed interest rate of 10%. How many years must Chopra leave that balance in the fund in order to get his desired $1 million?
(b) Assume that Elvira Lehman desires to accumulate $1 million in 15 years using her money market fund balance of $239,392. At what interest rate must Elvira's investment compound annually?
![]() E6-11 (Evaluation of Purchase Options) Rossi Excavating Inc. is purchasing a bulldozer. The equipment has a price of €100,000. The manufacturer has offered a payment plan that would allow Rossi to make 10 equal annual payments of €15,582, with the first payment due one year after the purchase.
E6-11 (Evaluation of Purchase Options) Rossi Excavating Inc. is purchasing a bulldozer. The equipment has a price of €100,000. The manufacturer has offered a payment plan that would allow Rossi to make 10 equal annual payments of €15,582, with the first payment due one year after the purchase.
Instructions
(a) How much total interest will Rossi pay on this payment plan?
(b) Rossi could borrow €100,000 from its bank to finance the purchase at an annual rate of 8%. Should Rossi borrow from the bank or use the manufacturer's payment plan to pay for the equipment?
![]() E6-12 (Analysis of Alternatives) Brubaker Inc., a manufacturer of high-sugar, low-sodium, low-cholesterol TV dinners, would like to increase its market share in the Sunbelt. In order to do so, Brubaker has decided to locate a new factory in the Panama City area. Brubaker will either buy or lease a site depending upon which is more advantageous. The site location committee has narrowed down the available sites to the following three buildings.
E6-12 (Analysis of Alternatives) Brubaker Inc., a manufacturer of high-sugar, low-sodium, low-cholesterol TV dinners, would like to increase its market share in the Sunbelt. In order to do so, Brubaker has decided to locate a new factory in the Panama City area. Brubaker will either buy or lease a site depending upon which is more advantageous. The site location committee has narrowed down the available sites to the following three buildings.
Building A: Purchase for a cash price of $610,000, useful life 25 years.
Building B: Lease for 25 years with annual lease payments of $70,000 being made at the beginning of the year.
Building C: Purchase for $650,000 cash. This building is larger than needed; however, the excess space can be sublet for 25 years at a net annual rental of $6,000. Rental payments will be received at the end of each year. Brubaker Inc. has no aversion to being a landlord.
Instructions
In which building would you recommend that Brubaker Inc. locate, assuming a 12% cost of funds?
![]() E6-13 (Computation of Bond Liability) Messier Inc. manufactures cycling equipment. Recently, the vice president of operations of the company has requested construction of a new plant to meet the increasing demand for the company's bikes. After a careful evaluation of the request, the board of directors has decided to raise funds for the new plant by issuing €3,000,000 of 11% term corporate bonds on March 1, 2015, due on March 1, 2030, with interest payable each March 1 and September 1. At the time of issuance, the market interest rate for similar financial instruments is 10%.
E6-13 (Computation of Bond Liability) Messier Inc. manufactures cycling equipment. Recently, the vice president of operations of the company has requested construction of a new plant to meet the increasing demand for the company's bikes. After a careful evaluation of the request, the board of directors has decided to raise funds for the new plant by issuing €3,000,000 of 11% term corporate bonds on March 1, 2015, due on March 1, 2030, with interest payable each March 1 and September 1. At the time of issuance, the market interest rate for similar financial instruments is 10%.
![]() E6-14 (Computation of Pension Liability) Calder, Inc. is a furniture manufacturing company with 50 employees. Recently, after a long negotiation with the local labor union, the company decided to initiate a pension plan as a part of its compensation plan. The plan will start on January 1, 2015. Each employee covered by the plan is entitled to a pension payment each year after retirement. As required by accounting standards, the controller of the company needs to report the pension obligation (liability). On the basis of a discussion with the supervisor of the Personnel Department and an actuary from an insurance company, the controller develops the following information related to the pension plan.
E6-14 (Computation of Pension Liability) Calder, Inc. is a furniture manufacturing company with 50 employees. Recently, after a long negotiation with the local labor union, the company decided to initiate a pension plan as a part of its compensation plan. The plan will start on January 1, 2015. Each employee covered by the plan is entitled to a pension payment each year after retirement. As required by accounting standards, the controller of the company needs to report the pension obligation (liability). On the basis of a discussion with the supervisor of the Personnel Department and an actuary from an insurance company, the controller develops the following information related to the pension plan.

![]() E6-15 (Investment Decision) Derek Lee just received a signing bonus of $1,000,000. His plan is to invest this payment in a fund that will earn 6%, compounded annually.
E6-15 (Investment Decision) Derek Lee just received a signing bonus of $1,000,000. His plan is to invest this payment in a fund that will earn 6%, compounded annually.
Instructions
(a) If Lee plans to establish the DL Foundation once the fund grows to $1,898,000, how many years until he can establish the foundation?
(b) Instead of investing the entire $1,000,000, Lee invests $300,000 today and plans to make 9 equal annual investments into the fund beginning one year from today. What amount should the payments be if Lee plans to establish the $1,898,000 foundation at the end of 9 years?
![]() E6-16 (Retirement of Debt) Rual Fernandez borrowed $90,000 on March 1, 2013. This amount plus accrued interest at 12% compounded semiannually is to be repaid March 1, 2023. To retire this debt, Rual plans to contribute to a debt retirement fund five equal amounts starting on March 1, 2018, and for the next 4 years. The fund is expected to earn 10% per annum.
E6-16 (Retirement of Debt) Rual Fernandez borrowed $90,000 on March 1, 2013. This amount plus accrued interest at 12% compounded semiannually is to be repaid March 1, 2023. To retire this debt, Rual plans to contribute to a debt retirement fund five equal amounts starting on March 1, 2018, and for the next 4 years. The fund is expected to earn 10% per annum.
Instructions
How much must be contributed each year by Rual Fernandez to provide a fund sufficient to retire the debt on March 1, 2023?
![]() E6-17 (Computation of Amount of Rentals) Your client, Wyeth Leasing Company, is preparing a contract to lease a machine to Souvenirs Corporation for a period of 25 years. Wyeth has an investment cost of £421,087 in the machine, which has a useful life of 25 years and no salvage value at the end of that time. Your client is interested in earning an 11% return on its investment and has agreed to accept 25 equal rental payments at the end of each of the next 25 years.
E6-17 (Computation of Amount of Rentals) Your client, Wyeth Leasing Company, is preparing a contract to lease a machine to Souvenirs Corporation for a period of 25 years. Wyeth has an investment cost of £421,087 in the machine, which has a useful life of 25 years and no salvage value at the end of that time. Your client is interested in earning an 11% return on its investment and has agreed to accept 25 equal rental payments at the end of each of the next 25 years.
Instructions
You are requested to provide Wyeth with the amount of each of the 25 rental payments that will yield an 11% return on investment.
![]() E6-18 (Least Costly Payoff) Assume that Aoki Company has a contractual debt outstanding. Aoki has available two means of settlement: It can either make immediate payment of ¥3,500,000, or it can make annual payments of ¥400,000 for 15 years, each payment due on the last day of the year (yen in thousands).
E6-18 (Least Costly Payoff) Assume that Aoki Company has a contractual debt outstanding. Aoki has available two means of settlement: It can either make immediate payment of ¥3,500,000, or it can make annual payments of ¥400,000 for 15 years, each payment due on the last day of the year (yen in thousands).
Instructions
Which method of payment do you recommend, assuming an expected effective-interest rate of 8% during the future period?
![]() E6-19 (Least Costly Payoff) Assuming the same facts as those in E6-18 except that the payments must begin now and be made on the first day of each of the 15 years, what payment method would you recommend?
E6-19 (Least Costly Payoff) Assuming the same facts as those in E6-18 except that the payments must begin now and be made on the first day of each of the 15 years, what payment method would you recommend?
![]() E6-20 (Expected Cash Flows) For each of the following, determine the expected cash flows.
E6-20 (Expected Cash Flows) For each of the following, determine the expected cash flows.
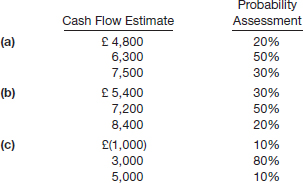
![]() E6-21 (Expected Cash Flows and Present Value) Angela Contreras is trying to determine the amount to set aside so that she will have enough money on hand in 2 years to overhaul the engine on her vintage used car. While there is some uncertainty about the cost of engine overhauls in 2 years, by conducting some research online, Angela has developed the following estimates.
E6-21 (Expected Cash Flows and Present Value) Angela Contreras is trying to determine the amount to set aside so that she will have enough money on hand in 2 years to overhaul the engine on her vintage used car. While there is some uncertainty about the cost of engine overhauls in 2 years, by conducting some research online, Angela has developed the following estimates.

Instructions
How much should Angela Contreras deposit today in an account earning 6%, compounded annually, so that she will have enough money on hand in 2 years to pay for the overhaul?
![]() E6-22 (Fair Value Estimate) Killroy Company owns a trade name that was purchased in an acquisition of McClellan Company. The trade name has a book value of $3,500,000, but according to IFRS, it is assessed for impairment on an annual basis. To perform this impairment test, Killroy must estimate the fair value of the trade name. (You will learn more about intangible asset impairments in Chapter 12.) It has developed the following cash flow estimates related to the trade name based on internal information. Each cash flow estimate reflects Killroy's estimate of annual cash flows over the next 8 years. The trade name is assumed to have no residual value after the 8 years. (Assume the cash flows occur at the end of each year.)
E6-22 (Fair Value Estimate) Killroy Company owns a trade name that was purchased in an acquisition of McClellan Company. The trade name has a book value of $3,500,000, but according to IFRS, it is assessed for impairment on an annual basis. To perform this impairment test, Killroy must estimate the fair value of the trade name. (You will learn more about intangible asset impairments in Chapter 12.) It has developed the following cash flow estimates related to the trade name based on internal information. Each cash flow estimate reflects Killroy's estimate of annual cash flows over the next 8 years. The trade name is assumed to have no residual value after the 8 years. (Assume the cash flows occur at the end of each year.)
![]()
(Interest rates are per annum unless otherwise indicated.)
![]() P6-1 (Various Time Value Situations) Answer each of these unrelated questions.
P6-1 (Various Time Value Situations) Answer each of these unrelated questions.
![]() (a) On January 1, 2015, Yang Corporation sold a building that cost ¥25,000,000 and that had accumulated depreciation of ¥10,000,000 on the date of sale. Yang received as consideration a ¥24,000,000 non-interest-bearing note due on January 1, 2018. There was no established exchange price for the building, and the note had no ready market. The prevailing rate of interest for a note of this type on January 1, 2015, was 9%. At what amount should the gain from the sale of the building be reported?
(a) On January 1, 2015, Yang Corporation sold a building that cost ¥25,000,000 and that had accumulated depreciation of ¥10,000,000 on the date of sale. Yang received as consideration a ¥24,000,000 non-interest-bearing note due on January 1, 2018. There was no established exchange price for the building, and the note had no ready market. The prevailing rate of interest for a note of this type on January 1, 2015, was 9%. At what amount should the gain from the sale of the building be reported?
(b) On January 1, 2015, Yang Corporation purchased 300 of the ¥100,000 face value, 9%, 10-year bonds of Walters Inc. The bonds mature on January 1, 2025, and pay interest annually beginning January 1, 2016. Yang purchased the bonds to yield 11%. How much did Yang pay for the bonds?
(c) Yang Corporation bought a new machine and agreed to pay for it in equal annual installments of ¥400,000 at the end of each of the next 10 years. Assuming that a prevailing interest rate of 8% applies to this contract, how much should Yang record as the cost of the machine?
(d) Yang Corporation purchased a special tractor on December 31, 2015. The purchase agreement stipulated that Yang should pay ¥2,000,000 at the time of purchase and ¥500,000 at the end of each of the next 8 years. The tractor should be recorded on December 31, 2015, at what amount, assuming an appropriate interest rate of 12%?
(e) Yang Corporation wants to withdraw ¥12,000,000 (including principal) from an investment fund at the end of each year for 9 years. What should be the required initial investment at the beginning of the first year if the fund earns 11%?
![]() P6-2 (Various Time Value Situations) Using the appropriate interest table, provide the solution to each of the following four questions by computing the unknowns.
P6-2 (Various Time Value Situations) Using the appropriate interest table, provide the solution to each of the following four questions by computing the unknowns.
![]() (a) What is the amount of the payments that Ned Winslow must make at the end of each of 8 years to accumulate a fund of $90,000 by the end of the eighth year, if the fund earns 8% interest, compounded annually?
(a) What is the amount of the payments that Ned Winslow must make at the end of each of 8 years to accumulate a fund of $90,000 by the end of the eighth year, if the fund earns 8% interest, compounded annually?
(b) Robert Hitchcock is 40 years old today and he wishes to accumulate $500,000 by his sixty-fifth birthday so he can retire to his summer place on Lake Hopatcong. He wishes to accumulate this amount by making equal deposits on his fortieth through his sixty-fourth birthdays. What annual deposit must Robert make if the fund will earn 12% interest compounded annually?
(c) Diane Ross has $20,000 to invest today at 9% to pay a debt of $47,347. How many years will it take her to accumulate enough to liquidate the debt?
(d) Cindy Houston has a $27,600 debt that she wishes to repay 4 years from today; she has $19,553 that she intends to invest for the 4 years. What rate of interest will she need to earn annually in order to accumulate enough to pay the debt?
![]() P6-3 (Analysis of Alternatives) Assume that Koh ShopMart has decided to surface and maintain for 10 years a vacant lot next to one of its stores to serve as a parking lot for customers. Management is considering the following bids involving two different qualities of surfacing for a parking area of 12,000 square yards (amounts in thousands).
P6-3 (Analysis of Alternatives) Assume that Koh ShopMart has decided to surface and maintain for 10 years a vacant lot next to one of its stores to serve as a parking lot for customers. Management is considering the following bids involving two different qualities of surfacing for a parking area of 12,000 square yards (amounts in thousands).
Bid A: A surface that costs ![]() 5.75 per square yard to install. This surface will have to be replaced at the end of 5 years. The annual maintenance cost on this surface is estimated at 25 cents per square yard for each year except the last year of its service. The replacement surface will be similar to the initial surface.
5.75 per square yard to install. This surface will have to be replaced at the end of 5 years. The annual maintenance cost on this surface is estimated at 25 cents per square yard for each year except the last year of its service. The replacement surface will be similar to the initial surface.
Bid B: A surface that costs ![]() 10.50 per square yard to install. This surface has a probable useful life of 10 years and will require annual maintenance in each year except the last year, at an estimated cost of 9 cents per square yard.
10.50 per square yard to install. This surface has a probable useful life of 10 years and will require annual maintenance in each year except the last year, at an estimated cost of 9 cents per square yard.
Instructions
Prepare computations showing which bid should be accepted by Koh ShopMart. You may assume that the cost of capital is 9%, that the annual maintenance expenditures are incurred at the end of each year, and that prices are not expected to change during the next 10 years.
![]() P6-4 (Evaluating Payment Alternatives) Ronald Long has just learned he has won a $500,000 prize in the lottery. The lottery has given him two options for receiving the payments. (1) If Ronald takes all the money today, the government will deduct taxes at a rate of 46% immediately. (2) The lottery offers Ronald a payout of 20 equal payments of $36,000 with the first payment occurring when Ronald turns in the winning ticket. Ronald will be taxed on each of these payments at a rate of 25%.
P6-4 (Evaluating Payment Alternatives) Ronald Long has just learned he has won a $500,000 prize in the lottery. The lottery has given him two options for receiving the payments. (1) If Ronald takes all the money today, the government will deduct taxes at a rate of 46% immediately. (2) The lottery offers Ronald a payout of 20 equal payments of $36,000 with the first payment occurring when Ronald turns in the winning ticket. Ronald will be taxed on each of these payments at a rate of 25%.
![]() P6-5 (Analysis of Alternatives) Julia Baker died, leaving to her husband Brent an insurance policy contract that provides that the beneficiary (Brent) can choose any one of the following four options.
P6-5 (Analysis of Alternatives) Julia Baker died, leaving to her husband Brent an insurance policy contract that provides that the beneficiary (Brent) can choose any one of the following four options.
(a) €55,000 immediate cash.
(b) €4,000 every 3 months payable at the end of each quarter for 5 years.
(c) €18,000 immediate cash and $1,800 every 3 months for 10 years, payable at the beginning of each 3-month period.
(d) €4,000 every 3 months for 3 years and $1,500 each quarter for the following 25 quarters, all payments payable at the end of each quarter.
Instructions
If money is worth 2½% per quarter, compounded quarterly, which option would you recommend that Brent exercise?
![]() P6-6 (Purchase Price of a Business) During the past year, Stacy McGill planted a new vineyard on 150 acres of land that she leases for €30,000 a year. She has asked you as her accountant to assist her in determining the value of her vineyard operation.
P6-6 (Purchase Price of a Business) During the past year, Stacy McGill planted a new vineyard on 150 acres of land that she leases for €30,000 a year. She has asked you as her accountant to assist her in determining the value of her vineyard operation.
The vineyard will bear no grapes for the first 5 years (1–5). In the next 5 years (6–10), Stacy estimates that the vines will bear grapes that can be sold for €60,000 each year. For the next 20 years (11–30) she expects the harvest will provide annual revenues of €110,000. But during the last 10 years (31–40) of the vineyard's life, she estimates that revenues will decline to €80,000 per year.
During the first 5 years the annual cost of pruning, fertilizing, and caring for the vineyard is estimated at €9,000; during the years of production, 6–40, these costs will rise to €12,000 per year. The relevant market rate of interest for the entire period is 12%. Assume that all receipts and payments are made at the end of each year.
Instructions
Dick Button has offered to buy Stacy's vineyard business by assuming the 40-year lease. On the basis of the current value of the business, what is the minimum price Stacy should accept?
![]() P6-7 (Time Value Concepts Applied to Solve Business Problems) Answer the following questions related to Dubois Inc.
P6-7 (Time Value Concepts Applied to Solve Business Problems) Answer the following questions related to Dubois Inc.
(a) Dubois Inc. has $600,000 to invest. The company is trying to decide between two alternative uses of the funds. One alternative provides $80,000 at the end of each year for 12 years, and the other is to receive a single lump-sum payment of $1,900,000 at the end of the 12 years. Which alternative should Dubois select? Assume the interest rate is constant over the entire investment.
(b) Dubois Inc. has completed the purchase of new iPad tablets. The fair value of the equipment is $824,150. The purchase agreement specifies an immediate down payment of $200,000 and semiannual payments of $76,952 beginning at the end of 6 months for 5 years. What is the interest rate, to the nearest percent, used in discounting this purchase transaction?
(c) Dubois Inc. loans money to John Kruk Corporation in the amount of $800,000. Dubois accepts an 8% note due in 7 years with interest payable semiannually. After 2 years (and receipt of interest for 2 years), Dubois needs money and therefore sells the note to Chicago National Bank, which demands interest on the note of 10% compounded semiannually. What is the amount Dubois will receive on the sale of the note?
(d) Dubois Inc. wishes to accumulate $1,300,000 by December 31, 2025, to retire bonds outstanding. The company deposits $200,000 on December 31, 2015, which will earn interest at 10% compounded quarterly, to help in the retirement of this debt. In addition, the company wants to know how much should be deposited at the end of each quarter for 10 years to ensure that $1,300,000 is available at the end of 2025. (The quarterly deposits will also earn at a rate of 10%, compounded quarterly.) (Round to even dollars.)
![]() P6-8 (Analysis of Alternatives) Ellison Inc., a manufacturer of steel school lockers, plans to purchase a new punch press for use in its manufacturing process. After contacting the appropriate vendors, the purchasing department received differing terms and options from each vendor. The Engineering Department has determined that each vendor's punch press is substantially identical and each has a useful life of 20 years. In addition, Engineering has estimated that required year-end maintenance costs will be £1,000 per year for the first 5 years, £2,000 per year for the next 10 years, and £3,000 per year for the last 5 years. Following is each vendor's sale package.
P6-8 (Analysis of Alternatives) Ellison Inc., a manufacturer of steel school lockers, plans to purchase a new punch press for use in its manufacturing process. After contacting the appropriate vendors, the purchasing department received differing terms and options from each vendor. The Engineering Department has determined that each vendor's punch press is substantially identical and each has a useful life of 20 years. In addition, Engineering has estimated that required year-end maintenance costs will be £1,000 per year for the first 5 years, £2,000 per year for the next 10 years, and £3,000 per year for the last 5 years. Following is each vendor's sale package.
Vendor A: £55,000 cash at time of delivery and 10 year-end payments of £18,000 each. Vendor A offers all its customers the right to purchase at the time of sale a separate 20-year maintenance service contract, under which Vendor A will perform all year-end maintenance at a one-time initial cost of £10,000.
Vendor B: Forty seminannual payments of £9,500 each, with the first installment due upon delivery. Vendor B will perform all year-end maintenance for the next 20 years at no extra charge.
Vendor C: Full cash price of £150,000 will be due upon delivery.
Instructions
Assuming that both Vendor A and B will be able to perform the required year-end maintenance, that Ellison's cost of funds is 10%, and the machine will be purchased on January 1, from which vendor should the press be purchased?
![]() P6-9 (Analysis of Business Problems) James Kirk is a financial executive with McDowell Enterprises. Although James Kirk has not had any formal training in finance or accounting, he has a “good sense” for numbers and has helped the company grow from a very small company ($500,000 sales) to a large operation ($45 million in sales). With the business growing steadily, however, the company needs to make a number of difficult financial decisions in which James Kirk feels a little “over his head.” He therefore has decided to hire a new employee with “numbers” expertise to help him. As a basis for determining whom to employ, he has decided to ask each prospective employee to prepare answers to questions relating to the following situations he has encountered recently. Here are the questions.
P6-9 (Analysis of Business Problems) James Kirk is a financial executive with McDowell Enterprises. Although James Kirk has not had any formal training in finance or accounting, he has a “good sense” for numbers and has helped the company grow from a very small company ($500,000 sales) to a large operation ($45 million in sales). With the business growing steadily, however, the company needs to make a number of difficult financial decisions in which James Kirk feels a little “over his head.” He therefore has decided to hire a new employee with “numbers” expertise to help him. As a basis for determining whom to employ, he has decided to ask each prospective employee to prepare answers to questions relating to the following situations he has encountered recently. Here are the questions.
(a) In 2015, McDowell Enterprises negotiated and closed a long-term lease contract for newly constructed truck terminals and freight storage facilities. The buildings were constructed on land owned by the company. On January 1, 2016, McDowell took possession of the leased property. The 20-year lease is effective for the period January 1, 2016, through December 31, 2035. Advance rental payments of $800,000 are payable to the lessor (owner of facilities) on January 1 of each of the first 10 years of the lease term. Advance payments of $400,000 are due on January 1 for each of the last 10 years of the lease term. McDowell has an option to purchase all the leased facilities for $1 on December 31, 2035. At the time the lease was negotiated, the fair value of the truck terminals and freight storage facilities was approximately $7,200,000. If the company had borrowed the money to purchase the facilities, it would have had to pay 10% interest. Should the company have purchased rather than leased the facilities?
(b) Last year, the company exchanged a piece of land for a zero–interest-bearing note. The note is to be paid at the rate of $15,000 per year for 9 years, beginning one year from the date of disposal of the land. An appropriate rate of interest for the note was 11%. At the time the land was originally purchased, it cost $90,000. What is the fair value of the note?
(c) The company has always followed the policy to take any cash discounts on goods purchased. Recently the company purchased a large amount of raw materials at a price of $800,000 with terms 1/10, n/30 on which it took the discount. McDowell has recently estimated its cost of funds at 10%. Should McDowell continue this policy of always taking the cash discount?
![]() P6-10 (Analysis of Lease vs. Purchase) Dunn Inc. owns and operates a number of hardware stores in the New England region. Recently, the company has decided to locate another store in a rapidly growing area of Maryland. The company is trying to decide whether to purchase or lease the building and related facilities.
P6-10 (Analysis of Lease vs. Purchase) Dunn Inc. owns and operates a number of hardware stores in the New England region. Recently, the company has decided to locate another store in a rapidly growing area of Maryland. The company is trying to decide whether to purchase or lease the building and related facilities.
Purchase: The company can purchase the site, construct the building, and purchase all store fixtures. The cost would be $1,850,000. An immediate down payment of $400,000 is required, and the remaining $1,450,000 would be paid off over 5 years at $350,000 per year (including interest; payments made at end of year). The property is expected to have a useful life of 12 years, and then it will be sold for $500,000. As the owner of the property, the company will have the following out-of-pocket expenses each period.

Lease: First Bank has agreed to purchase the site, construct the building, and install the appropriate fixtures for Dunn Inc. if Dunn will lease the completed facility for 12 years. The annual costs for the lease would be $270,000. Dunn would have no responsibility related to the facility over the 12 years. The terms of the lease are that Dunn would be required to make 12 annual payments (the first payment to be made at the time the store opens and then each following year). In addition, a deposit of $100,000 is required when the store is opened. This deposit will be returned at the end of the twelfth year, assuming no unusual damage to the building structure or fixtures.
Currently, the cost of funds for Dunn Inc. is 10%.
Instructions
Which of the two approaches should Dunn Inc. follow?
![]() P6-11 (Pension Funding) You have been hired as a benefit consultant by Jean Barclay, the owner of Attic Angels. She wants to establish a retirement plan for herself and her three employees. Jean has provided the following information. The retirement plan is to be based upon annual salary for the last year before retirement and is to provide 50% of Jean's last-year annual salary and 40% of the last-year annual salary for each employee. The plan will make annual payments at the beginning of each year for 20 years from the date of retirement. Jean wishes to fund the plan by making 15 annual deposits beginning January 1, 2015. Invested funds will earn 12% compounded annually. Information about plan participants as of January 1, 2015, is as follows.
P6-11 (Pension Funding) You have been hired as a benefit consultant by Jean Barclay, the owner of Attic Angels. She wants to establish a retirement plan for herself and her three employees. Jean has provided the following information. The retirement plan is to be based upon annual salary for the last year before retirement and is to provide 50% of Jean's last-year annual salary and 40% of the last-year annual salary for each employee. The plan will make annual payments at the beginning of each year for 20 years from the date of retirement. Jean wishes to fund the plan by making 15 annual deposits beginning January 1, 2015. Invested funds will earn 12% compounded annually. Information about plan participants as of January 1, 2015, is as follows.
Jean Barclay, owner: Current annual salary of £48,000; estimated retirement date January 1, 2040.
Colin Davis, flower arranger: Current annual salary of £36,000; estimated retirement date January 1, 2045.
Anita Baker, sales clerk: Current annual salary of £18,000; estimated retirement date January 1, 2035.
Gavin Bryars, part-time bookkeeper: Current annual salary of £15,000; estimated retirement date January 1, 2030.
In the past, Jean has given herself and each employee a year-end salary increase of 4%. Jean plans to continue this policy in the future.
Instructions
(a) Based upon the above information, what will be the annual retirement benefit for each plan participant? (Round to the nearest pound.) (Hint: Jean will receive raises for 24 years.)
(b) What amount must be on deposit at the end of 15 years to ensure that all benefits will be paid? (Round to the nearest pound.)
(c) What is the amount of each annual deposit Jean must make to the retirement plan?
![]()
 P6-12 (Pension Funding) Tim Buhl, newly appointed controller of STL, is considering ways to reduce his company's expenditures on annual pension costs. One way to do this is to switch STL's pension fund assets from First Security to NET Life. STL is a very well-respected computer manufacturer that recently has experienced a sharp decline in its financial performance for the first time in its 25-year history. Despite financial problems, STL still is committed to providing its employees with good pension and postretirement health benefits.
P6-12 (Pension Funding) Tim Buhl, newly appointed controller of STL, is considering ways to reduce his company's expenditures on annual pension costs. One way to do this is to switch STL's pension fund assets from First Security to NET Life. STL is a very well-respected computer manufacturer that recently has experienced a sharp decline in its financial performance for the first time in its 25-year history. Despite financial problems, STL still is committed to providing its employees with good pension and postretirement health benefits.
Under its present plan with First Security, STL is obligated to pay £43 million to meet the expected value of future pension benefits that are payable to employees as an annuity upon their retirement from the company. On the other hand, NET Life requires STL to pay only £35 million for identical future pension benefits. First Security is one of the oldest and most reputable insurance companies in Europe. NET Life has a much weaker reputation in the insurance industry. In pondering the significant difference in annual pension costs, Buhl asks himself, “Is this too good to be true?”
Instructions
Answer the following questions.
(a) Why might NET Life's pension cost requirement be £8 million less than First Security's requirement for the same future value?
(b) What ethical issues should Tim Buhl consider before switching STL's pension fund assets?
(c) Who are the stakeholders that could be affected by Buhl decision?
![]() P6-13 (Expected Cash Flows and Present Value) Danny's Lawn Equipment sells high-quality lawn mowers and offers a 3-year warranty on all new lawn mowers sold. In 2015, Danny sold $300,000 of new specialty mowers for golf greens for which Danny's service department does not have the equipment to do the service. Danny has entered into an agreement with Mower Mavens to perform all warranty service on the special mowers sold in 2015. Danny wishes to measure the fair value of the agreement to determine the warranty liability for sales made in 2015. The controller for Danny's Lawn Equipment estimates the following expected warranty cash outflows associated with the mowers sold in 2015.
P6-13 (Expected Cash Flows and Present Value) Danny's Lawn Equipment sells high-quality lawn mowers and offers a 3-year warranty on all new lawn mowers sold. In 2015, Danny sold $300,000 of new specialty mowers for golf greens for which Danny's service department does not have the equipment to do the service. Danny has entered into an agreement with Mower Mavens to perform all warranty service on the special mowers sold in 2015. Danny wishes to measure the fair value of the agreement to determine the warranty liability for sales made in 2015. The controller for Danny's Lawn Equipment estimates the following expected warranty cash outflows associated with the mowers sold in 2015.

Instructions
Using expected cash flow and present value techniques, determine the value of the warranty liability for the 2015 sales. Use an annual discount rate of 5%. Assume all cash flows occur at the end of the year.
![]() P6-14 (Expected Cash Flows and Present Value) At the end of 2015, Sawyer Company is conducting an impairment test and needs to develop a fair value estimate for machinery used in its manufacturing operations. Given the nature of Sawyer's production process, the equipment is for special use. (No second-hand market values are available.) The equipment will be obsolete in 2 years, and Sawyer's accountants have developed the following cash flow information for the equipment.
P6-14 (Expected Cash Flows and Present Value) At the end of 2015, Sawyer Company is conducting an impairment test and needs to develop a fair value estimate for machinery used in its manufacturing operations. Given the nature of Sawyer's production process, the equipment is for special use. (No second-hand market values are available.) The equipment will be obsolete in 2 years, and Sawyer's accountants have developed the following cash flow information for the equipment.

Instructions
Using expected cash flow and present value techniques, determine the fair value of the machinery at the end of 2015. Use a 6% discount rate. Assume all cash flows occur at the end of the year.
![]() P6-15 (Fair Value Estimate) Murphy Mining Company recently purchased a quartz mine that it intends to work for the next 10 years. According to state environmental laws, Murphy must restore the mine site to its original natural prairie state after it ceases mining operations at the site. To properly account for the mine, Murphy must estimate the fair value of this environmental liability. This amount will be recorded as a liability and added to the value of the mine on Murphy's books. (You will learn more about these environmental liabilities in Chapters 10 and 13.)
P6-15 (Fair Value Estimate) Murphy Mining Company recently purchased a quartz mine that it intends to work for the next 10 years. According to state environmental laws, Murphy must restore the mine site to its original natural prairie state after it ceases mining operations at the site. To properly account for the mine, Murphy must estimate the fair value of this environmental liability. This amount will be recorded as a liability and added to the value of the mine on Murphy's books. (You will learn more about these environmental liabilities in Chapters 10 and 13.)
There is no active market for environmental liabilities such as these, but Murphy has developed the following cash flow estimates based on its prior experience in mining-site restoration. It will take 3 years to restore the mine site when mining operations cease in 10 years. Each estimated cash outflow reflects an annual payment at the end of each year of the 3-year restoration period.

Instructions
(a) What is the estimated fair value of Murphy's environmental liability? Murphy determines that the appropriate discount rate for this estimation is 5%. Round calculations to the nearest dollar.
(b) Is the estimate developed for part (a) a Level 1 or Level 3 fair value estimate? Explain.
![]()
FINANCIAL REPORTING
Financial Reporting Problem
Marks and Spencer plc (M&S)
The financial statements of M&S (GBR) are presented in Appendix A. The company's complete annual report, including the notes to the financial statements, is available online.
Instructions
Refer to M&S's financial statements and the accompanying notes to answer the following questions.
(a) Examining each item in M&S's statement of financial position, identify those items that require present value, discounting, or interest computations in establishing the amount reported. (The accompanying notes are an additional source for this information.)
(b)(1) What interest rates are disclosed by M&S as being used to compute interest and present values?
(2) Why are there so many different interest rates applied to M&S's financial statement elements (assets, liabilities, revenues, and expenses)?
Financial Statement Analysis Case
Assume the following information for Alta Gas (CAN). In 2014, Alta estimated the cash inflows from its oil and gas producing properties to be $375,000 per year. During 2015, a write-down caused the estimate to be decreased to $275,000 per year. Production costs (cash outflows) associated with all these properties were estimated to be $125,000 per year in 2014, but this amount was revised to $155,000 per year in 2015.
Instructions
(Assume that all cash flows occur at the end of the year.)
(a) Calculate the present value of net cash flows for 2014–2016 (three years), using the 2014 estimates and a 10% discount factor.
(b) Calculate the present value of net cash flows for 2015–2017 (three years), using the 2015 estimates and a 10% discount factor.
(c) Compare the results using the two estimates. Is information on future cash flows from oil- and gas-producing properties useful, considering that the estimates must be revised each year? Explain.
Accounting, Analysis, and Principles
Johnson Co. accepts a note receivable from a customer in exchange for some damaged inventory. The note requires the customer to make 10 semiannual installments of $50,000 each. The first installment begins six months from the date the customer took delivery of the damaged inventory. Johnson's management estimates that the fair value of the damaged inventory is $320,883.
Accounting
(a) What interest rate is Johnson implicitly charging the customer? Express the rate as an annual rate but assume semiannual compounding.
(b) At what dollar amount do you think Johnson should record the note receivable on the day the customer takes delivery of the damaged inventory?
Analysis
Assume the note receivable for damaged inventory makes up a significant portion of Johnson's assets. If interest rates increase, what happens to the fair value of the receivable? Briefly explain why.
Principles
The IASB has issued an accounting standard that allows companies to report assets such as notes receivable at fair value. Discuss how fair value versus historical cost potentially involves a trade-off of one desired quality of accounting information against another.
IFRS BRIDGE TO THE PROFESSION
Professional Research
At a recent meeting of the accounting staff in your company, the controller raised the issue of using present value techniques to conduct impairment tests for some of the company's fixed assets. Some of the more senior members of the staff admitted having little knowledge of present value concepts in this context, but they had heard about an appendix to an IFRS that provides some guidance. As the junior staff in the department, you have been asked to conduct some research of the authoritative literature on this topic and report back at the staff meeting next week.
Instructions
Access the IFRS authoritative literature at the IASB website (http://eifrs.iasb.org/) (you may register for free eIFRS access at this site). When you have accessed the documents, you can use the search tool in your Internet browser to respond to the following questions. (Provide paragraph citations.)
(a) Identify the components of present value measurement.
(b) Briefly describe the differences between the “traditional” and “expected cash flow” approaches to present value.
(c) What are the factors that should be taken into account when an asset-specific discount rate is not available from the market?
Professional Simulation
In this simulation, you are asked to address questions concerning the application of time value of money concepts to accounting problems. Prepare responses to all parts.

TABLE 6-1 FUTURE VALUE OF 1 (FUTURE VALUE OF A SINGLE SUM)
TABLE 6-2 PRESENT VALUE OF 1 (PRESENT VALUE OF A SINGLE SUM)

TABLE 6-3 FUTURE VALUE OF AN ORDINARY ANNUITY OF 1

TABLE 6-4 PRESENT VALUE OF AN ORDINARY ANNUITY OF 1
TABLE 6-5 PRESENT VALUE OF AN ANNUITY DUE OF 1

1IFRS addresses present value as a measurement basis for a broad array of transactions, such as accounts and loans receivable [2], leases [3], postretirement benefits [4], asset impairments [5], and share-based compensation [6].
2Many regulatory frameworks require the disclosure of interest rates on an annual basis in all contracts. That is, instead of stating the rate as “1% per month,” contracts must state the rate as “12% per year” if it is simple interest or “12.68% per year” if it is compounded monthly.
3Business mathematics and business finance textbooks traditionally state simple interest as I(interest) = P(principal) × R(rate) × T(time).
4Because interest is theoretically earned (accruing) every second of every day, it is possible to calculate interest that is compounded continuously. Using the natural, or Napierian, system of logarithms facilitates computations involving continuous compounding. As a practical matter, however, most business transactions assume interest to be compounded no more frequently than daily.
5The formula for calculating the effective rate, in situations where the compounding frequency (n) is greater than once a year, is as follows.
![]()
To illustrate, if the stated annual rate is 8% compounded quarterly (or 2% per quarter), the effective annual rate is:
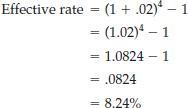
6In other words, the interest rate(s) used to discount cash flows should reflect assumptions that are consistent with those inherent in the estimated cash flows. Otherwise, the effect of some assumptions will be double-counted or ignored. For example, a discount rate of 12% might be applied to contractual cash flows of a loan receivable. That rate reflects expectations about future defaults from loans with particular characteristics. That same 12% rate should not be used to discount expected cash flows because those cash flows already reflect assumptions about future defaults. [8]
7As indicated in the beginning of the chapter, there are a number of situations where present value computations are needed. A common situation (and the one the IASB commented on specifically) is when a company is determining whether its assets are impaired. Impairment occurs when the carrying value of an asset such as equipment is not recoverable. One method used to determine the recoverable amount is the value-in-use approach. The value-in-use approach computes the present value of the expected cash flows to be generated using the asset. The discussion of this method will be examined in later chapters on non-current assets.