Chapter 12

Monte Carlo Methods

Out of intense complexities intense simplicities emerge.

—Winston Churchill

Many problems in finance do not have deterministic solutions because of the inherently stochastic nature of the problems’ underlying behaviors. In these cases, solutions are interpreted probabilistically and our interest centers on the statistical properties of the conclusions we draw from studying certain statistics of interest. Monte Carlo methods are algorithms that perform repeated random samplings in which sample properties provide us insight into the sampling distributions of these statistics of interest. One particular application, for example, relates to credit risk and the sensitivity of joint default on bonds to changes in the correlation across bonds—the probability, say, that bonds A, B, and C default at the same time. The relationship of interest in this case is the dependence of joint default risk on the correlation of returns across the bonds. We study this problem in detail further on.

Monte Carlo methods are the topic of a voluminous literature in the sciences and my intent here is not to cover that literature but to introduce you to this important class of models as they relate to our study of risk. Although there is no hard consensus on what exactly constitutes a Monte Carlo study, they all share some common elements: Given a set of known parameters—means, volatilities, and correlations, for example—we generate samples of new observations consistent with the distributional properties of these parameters using random draws from a known distribution and then compute deterministic solutions to a stated problem. This process is repeated, generating samples of solutions whose properties are the object of our study. In this introductory section, I present three examples, in increasing order of complexity, that develop some basic elements of the Monte Carlo method. We then move on to address directly the distributional properties of the random number generation process and, in particular, non-normal distributions. This will set us up to discuss and develop copulas. Our applications in this chapter are directly relevant to our discussion on risk.

---

Example 12.1: Generating Random Numbers—Estimating Π

A simple computational application that estimates the value of pi will serve as an introduction to this technique (Kalos 2008). Figure 12.1 shows the unit circle circumscribed within a unit square. The diameter, d, of the circle and the width of the square are both equal to one. The area of the square is therefore d² and the area of the circle is πr² = π(d/2)². The ratio of the area of the circle to that of the square is therefore π/4.

Figure 12.1 Circle within the Unit Square

Now, suppose we were to draw a sample of pairs of numbers from the uniform distribution defined over the unit interval (between zero and one). Each pair is a coordinate in the x-y plane depicted in Figure 12.1, that is, a point within the unit square. There is a sample of 100 draws provided in the Chapter 12 worksheet examples on the sheet titled “Estimating pi.” We will use these random draws to estimate pi. But, first, some background. The equation for a circle is given by . 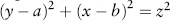In Figure 12.1, the lower left coordinate is the origin (y,x) = (0,0), the midpoint is (a,b) = (0.5,0.5), and the radius z = 0.5. We can therefore locate the sample points withinthe circle by counting those points (x-y coordinate pairs) that satisfy the following inequality: . 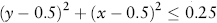To do this in Excel, we use the IF function in column C of the spreadsheet, specifically, =IF(a² – 0.5)^2 + (b² – 0.5)^2 ≤ 0.25,1,0). The count of all these points is the sum of column C. We divide the count by the total points (all of which fall in the square) and multiply by 4. This provides an estimate of pi. This value is given in cell D2 on the spreadsheet. Pressing F9 refreshes the sheet, generating another estimate. Larger samples give a more precise estimate.

Clearly, we do not need to go to this effort to estimate pi, whose value we already know. Rather, this simple example illustrates how random sampling from a known distribution can be used to estimate the value of an unknown parameter and, in that sense, it serves as an introduction to the intuition on Monte Carlo procedures.

---

---

Example 12.2: Confirming the Central Limit Theorem

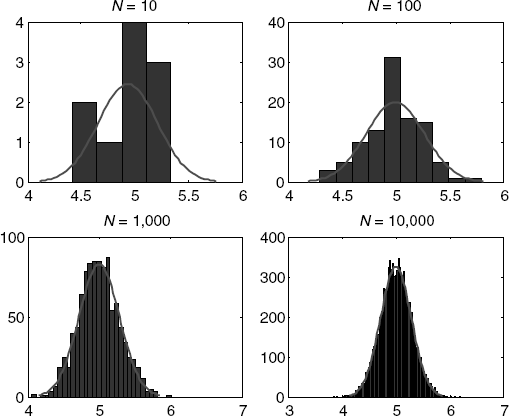
Let's expand our method. Consider a problem whose solution is now a function of the size of the randomly drawn sample. In this case, we want to demonstrate a result of the central limit theorem, which states that the distribution of the sample mean is normally distributed as the sample size increases. Figure 12.2 illustrates this result, using four sample sizes with the normal density overlaid.

Figure 12.2 Distribution of the Sample Mean

The central limit theorem is one of the most powerful results in statistics. It states that no matter what the underlying distribution a random sample is drawn from, the distribution of the sample mean follows a normal distribution. Think of this for a moment. It says that no matter what the shape of the probability distribution we draw data from, the mean of that sample will follow the bell-shaped normal density. This is an asymptotic result, as N → ∞, which I intend to show further on. That means that we can safely appeal to test statistics for hypotheses involving means using a single distribution—the normal distribution. The results in Figure 12.2 were generated from a Monte Carlo experiment drawing from the uniform distribution defined over the range 0 to 10 (which assigns equal probability of drawing any number in the 0 to 10 interval).

The experiment draws 100 values from the uniform distribution and estimates the sample mean. The population mean of uniform distribution in our example is equal to (b – a))/(2) = ((10 – 0))/2 = 5. The central limit theorem states that if we repeat this experiment N times, drawing new samples of size 100 and estimating the mean, then the distribution of these means is normal. With N = 10, we see from Figure 12.2 that we are far from normality. However, it is clear that as N increases, the distribution of the sample mean indeed becomes normal in the limit around its true population mean. Asymptotically, the distribution of the sample mean collapses to the population mean as N approaches infinity. The central limit theorem justifies the use of sample statistics based on the normal density function (z, t, χ², and F statistics) and although it, too, is proved in mathematics, the Monte Carlo demonstration used here helps illustrate the usefulness of sampling experiments to derive properties of various estimators.

---

---

Example 12.3: Credit Default Risk

Let's shift to an application that has more significance to finance. Consider three bonds (A, B, and C) which have mean monthly default probability, in percent, μ = (0.25, 0.33, 0.42), respectively, with monthly volatilities of (1.5, 2, 2.6) percent, respectively. For example, the probability that bond A will default in any given month is one-quarter of 1 percent. A two-standard deviation positive shock to that probability puts default risk at 3.25 percent per month. We are interested in the joint default sensitivity of these bonds to the correlations in their returns. To that end, we begin with a correlation matrix that shows default rates to be highly correlated as shown in the following correlation matrix:

We showed previously that the covariance matrix V can be expressed as the product: S^∗C^∗S, where S is a diagonal matrix of volatilities:

Our objective is to try to determine how many times in a 10-year period that this market will fail. Failure is defined here as a joint occurrence that all three bonds default jointly. We arbitrarily define a bond default if its monthly default probability exceeds an arbitrary upper bound exceeding the ninety-seventh percentile of its default distribution. If all three bonds default simultaneously in any given month, then we have joint failure (what is called systemic failure). Since we are simulating 10 years of monthly default probabilities, we are interested in estimating the incidence of systemic failure over a decade and, moreover, the sensitivity of systemic failure to changes in the correlations given in C.

How do we go about accomplishing this task? Well, clearly we wish to generate a series of default probabilities for these three bonds that have means μ, volatilities given by the diagonal matrix S, and correlations consistent with C. The Cholesky decomposition of V is the upper triangular matrix P such that V = P′^∗P. For the V given here, P is equal to:

This suggests that multiplying P times a 3 × 1 vector of random draws from the standard normal density (z₁,z₂,z₃)’ and adding μ will give us a simulated set of returns with expected value equal to μ and variance-covariance equal to V. The important assumption here (and one that is perhaps quite restrictive) is that defaults are multivariate normal. Thus, the z's are draws from a multivariate normal distribution with mean µ and covariance V. That is,

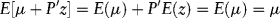
This holds because E(z) = 0, since the individual z_i are independent draws from the standard normal distribution. Likewise, the variance is:

which holds because the variance of μ is zero (it is a parameter) and the variance of z is one (more precisely, E(zz′) is the identity matrix). The Monte Carlo design therefore consists of repeated draws z from N(0,1). For our first trial, therefore, we draw 120 triplets from N(0,1), where the simulated return in each of the 120 draws is a 3 × 1 vector x_i = μ + P′z_i for i = 1,..., 120. There will be 120 cases—one for each month in our 10-year experiment. The entire sample is a 3 × 120 matrix of probabilities, in which each column represents a joint probability of default and each row corresponds to a single bond. Thus, each triplet (column) is a realization under the multivariate normal density with parameters μ and V. The probability of seeing these values can be computed using the normal cumulative density—that is, the probability that z is greater than or equal to the simulated value. In Excel, this is done with the NORMDIST(x) function. Applying this function to our simulated returns yields probabilities. We care about those that lie above the ninety-seventh percentile and count the total number of columns for which all three bond default probabilities jointly exceed this cutoff point and divide by 120.

The experiment is then repeated, changing the off-diagonal elements (the correlations) given in C. Let's assume for simplicity of exposition here that the correlations are the same across bonds A and B, B and C, and A and C. In this manner, we need only change a single value in the correlation matrix. We range this single value from 0 to 0.99 in increments of one basis point, creating 100 cases over which the correlation matrix varies and counting up the proportion of the 120 cases in each that have joint default events. Figure 12.3 shows the relationship between the joint probability of credit default and returns correlation. In this example, the probability is convex in the correlations.

Figure 12.3 Credit Default Systemic Risk

The experiment can be summarized in the following steps:

Define the parameters (means, correlations, volatilities, covariances).

Solve for the Cholesky decomposition of the covariance matrix.

Using the mean vector and the Cholesky decomposition, generate a sample of size T × k, where k is the number of assets, by repeating x_i = μ + Cholesky^∗randn(0,1), where randn(0,1) is a k × 1 vector of standard normal random numbers and μ is a k × 1 vector of mean returns and Cholesky is a k × k matrix. Repeat T times.

Convert these simulated returns to cumulative probabilities using NORMDIST(x).

Count the cases that fall into the appropriate tail region.

Change the correlations and repeat all of the preceding steps.

---