Pricing European Call Options

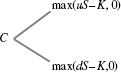
Let's use the idea of a replicating portfolio to derive the value of a call option. We'll begin with a single period problem depicted in Figure 16.5. Think of a stock whose spot price S can go up at the end of one period by a factor u to the level uS or can go down by a factor d to dS. I will derive the parameters u and d in Chapter 17. Moreover, suppose that the return on a risk-free loan is . Thus, we have the payout shown in Figure 16.5.

Figure 16.5 Single Period Payout Space

The call option will have the payout space given in Figure 16.6.

Figure 16.6 Call Payout Space

We want to use a combination of an investment in the stock and the risk-free asset to mimic the value of the call option. Letting Cu and Cd stand for the value of the call should the stock price rise or fall, respectively, then our aim is construct a riskless portfolio consisting of a long position of $x in the stock and $b in the risk-free asset plus a short position in one call option. If stock prices rise, we get the first of the following two equations; if they fall, we get the second equation. No arbitrage means that these will hold (otherwise, we can profit with no risk by selling calls in exchange for stock and vice versa). The question is how much of the stock do we need (x) and how much do we lend (b)? Thus, we solve the following for x and b:

We can solve the following system for x and b:

This has the solution given by:

Therefore, the replicating portfolio is the sum:

Substituting and recognizing that simplifies this as:

Finally, realizing that must equal the value of the call, we immediately have the result:

Here the parameter q plays the role of a probability in determining the expected value. This says that the current period value of the call option is the discounted expected value of the next period valuations (see Figures 16.5 and 16.6). Notice that q does not include the stock's expected return and this feature is what makes this risk-neutral pricing because it does not depend in any way on our preferences toward risk. This is our major result. As an example, take the case of a one-month call option with current underlying share price and a strike price . Note that the option is currently in the money. Assume that the annual risk-free rate is 10 percent, implying that the monthly risk-free rate return is and let's assume the up and down movement multipliers are and . From these values, we solve . Figure 16.7 illustrates the possible share prices one month out along with the call option values. Let's discuss how these numbers were arrived at.

It's easy to see how the two share prices are arrived at. and . The call option values corresponding to these two prices are derived from . If the share price rises to $1.06, then the call has value . Otherwise, if the share price falls to $0.94, the call has value $0.04. The value of the call presently is a weighted average of these two terminal call option values with weights q and . This gives us:

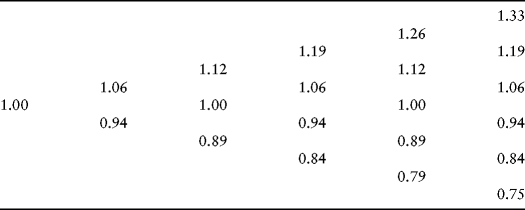
This says that the fair price for the option to buy a currently priced $1 share of stock one month from now for $0.9 is 11 cents. A multiple-period model of stock prices is a natural extension, which we see in Figure 16.8.

---

Example 16.1

Let's extend our one-period example to a five-month call option on the same stock with the same parameter values used in the previous example. Again, stock price dynamics are binomial; they either go up by a factor of or down by a factor of . We are now looking at the following stock price mapping:

Figure 16.9 Multiperiod Stock Dynamic

Working from the highlighted terminal nodes in Figure 16.9, we get the terminal nodes for the call values as max . For example, the call value corresponding to a stock price outcome of $1.33 (with strike price $0.90) will be max which is the highest value of the call option given by the top entry in the last column of Figure 16.10. After filling in the remaining elements of this column, we work backward, computing the call value at each interior node as the discounted weighted average of the two possible immediate future call values. So, for example, conditional on the terminal period's prices being $1.33 or $1.19 with corresponding call values $0.43 and $0.29, respectively, the penultimate period value of the call option is:

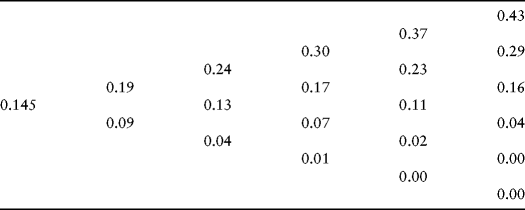
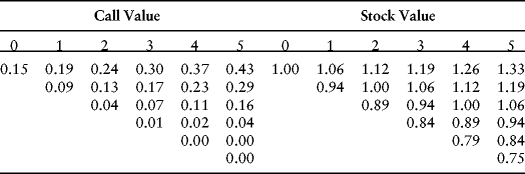
Figure 16.10 Call Option Value

Completing the tree backward to the current period says that the five-month call option on a one dollar stock is worth about 15 cents at present. It's a lot easier to work computationally with spreadsheets if we construct our lattices as depicted here. We'll use this lattice format here on out.

Go to the companion website for more details.

---